一类含未知函数重积分竞赛题的研究与推广

欧阳资考，石勇国，廖 为，刁 琴

(内江师范学院 数学与信息科学学院，四川 内江 641100)

0 引言

很多学者重视重积分教学研究. 周敏等[1]利用整体运算与边界运算之间的联系,类比推导了格林公式，以统一的观点看待牛顿-莱布尼兹公式、格林公式、高斯公式与斯托克斯公式； 袁荣[2]介绍了极坐标变换计算二重积分的方法和技巧；蒋银山[3]给出了三重积分的几种常用计算方法； 草吉利等[4]给出了高斯公式另一种简捷的证明方法； 张辉等[5]介绍了第一类曲面积分计算的八种常用方法； 滕吉红等[6]结合历届全国大学生数学竞赛试题，统计了重积分换元法的考查频率和考查方式； 尹逊波等[7]系统给出了重积分坐标变换的公式，并且运用到近几年全国大学生数学竞赛试题； 张立卓等[8]说明了高斯公式计算曲面积分需要注意公式成立的条件；石勇国等[9]给出了计算定积分的一些方法.

重积分计算的难点涉及利用对称性、恰当的坐标变换、选择使用格林公式或高斯公式等. 试题的综合性强，应用广泛. 重积分计算在全国大学生数学竞赛中出现频率较高，其中一类含有未知函数的重积分竞赛题经常出现，分值较大，例如：

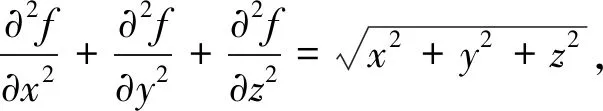
这类重积分竞赛题有两个明显的难点，其一是题目中均有关于未知函数f的微分方程，但是f没有给出显式表达式，无法直接求解；其二是重积分计算公式与其他知识点结合,例如，例1与极限结合，例2与无理分式结合，例3将二重积分扩展到三重积分.

重积分计算可化为累次积分或利用坐标变换化为累次积分进行计算. 利用对称性，以及格林公式、高斯公式、斯托克斯公式是化简重积分的重要技巧与手段.

本文给出这类题型一般性的推广.利用格林公式、高斯公式，将上述题目中未知函数f进行替换求解. 给出了两个比较自然的解法，并且对上述题目进行求解与证明.

1 推广的结果

先给出两个用到的定理.

引理1设闭区域D由分片光滑的曲线L围成，函数P(x,y),Q(x,y)在D上具有一阶连续偏导数，则

或

其中L是取D的边界曲线正向，cosα,cosβ是L上点(x,y)处与L方向一致的切向量的方向余弦.

引理2设空间闭区域Ω由分片光滑的曲面S围成，函数P(x,y,z),Q(x,y,z),R(x,y,z)在Ω上具有一阶连续偏导数，则

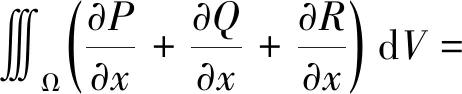
或

S(Pcosα+Qcosβ+Rcosγ)dS，

其中S是Ω的整个边界曲面的外侧，cosα,cosβ,cosγ是S上点(x,y,z)处的外法线向量的方向余弦.

上面两个定理中的公式分别称为格林公式与高斯公式.

下面给出两个推广的结论.

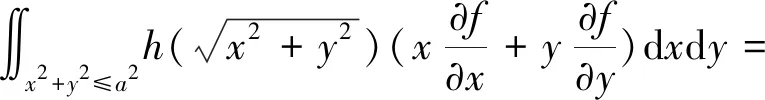
证明首先利用坐标变换进行化简，再利用格林公式，将曲线积分转化为二重积分，令x=rcosθ，y=rsinθ，则

证毕.

下面将定理1推广到三维情形.

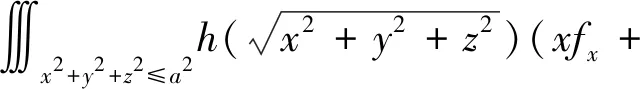
证首先利用球面坐标变换进行化简，再利用高斯公式，将曲面积分转化为三重积分，令x=rsinφcosθ，y=rsinφsinθ，z=rcosφ，则

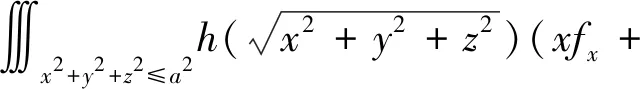
证毕.

2 结果的应用

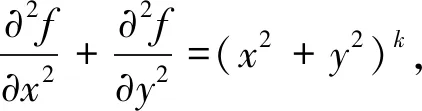
解令

g(x,y)=(x2+y2)k=r2k，则

根据定理1，则

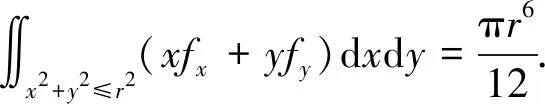
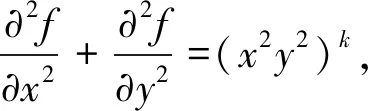
解令x=rcosθ，y=rsinθ，h(r)=r2l，g(x,y)=(x2y2)k=r2ksin2kθcoskθ，则

根据定理1，则

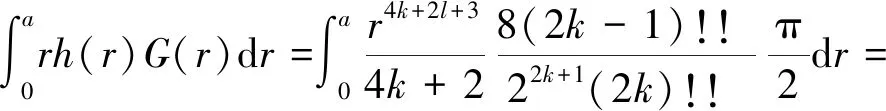
特别地，对于例2，取

得

∭x2+y2+z2≤a2(x2+y2+z2)l(xfx+
yfy+zfz)dxdydz.

解令x=rsinφcosθ，y=rsinφsinθ，z=rcosφ，h(r)=r2l，则

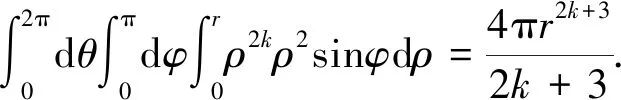
根据定理2，则

∭x2+y2+z2≤a2(x2+y2+z2)l(xfx+

yfy+zfz)dxdydz.

解令x=rsinφcosθ，y=rsinφsinθ，z=rcosφ，h(r)=r2l，则

根据定理2，则

3 结论

本文对部分全国大学生数学竞赛试题进行分析，总结了含有未知函数二重积分竞赛题的求解方法，给出了一般性的推广，展示一种统一的求解方法.该推广以及方法能够帮助大学生理解该类竞赛试题出题的意图，同时，提高学生的计算能力以及知识点综合运用能力.