弹簧板式明渠测流装置的水力特性
万里,李永业,张港,蔡鸿儒,张雪兰,杨小妮
(太原理工大学水利科学与工程学院,山西 太原 030024)
随着经济社会的快速发展,中国用水量逐步增长,其中农业用水量占全国用水总量的61%,但是农田灌溉水有效利用系数仅为0.559,节水灌溉仍有很大的发展空间[1].中国灌区量水设施不完善,施工工艺复杂,部分地区设施老化严重,量测精度降低,研发新型量水方法可以有效计量农田灌溉水,从而提高灌溉水利用效率,达到节水灌溉的目的[2].传统的量水方法利用现存的大量水工建筑物(闸门)进行量水,这种方法测流精度较低[3].HAGER[4]通过试验提出在渠道中利用结构简单的圆柱体测量流量,之后的众多学者对量水柱的结构进行不断改进,如带有入口导向的五棱柱[5]、机翼型量水柱[6]、圆头及圆头带尾翼式量水柱[7]等,推导出一系列与之相对应的测流公式,但量水柱量水的水头损失较大,不易推广.TARIQ等[8]针对铰链杆在渠道中受水流作用偏转现象进行研究,以偏转角计算渠道中心理论速度,从而得到了渠道断面平均流速.周义仁等[9]设计了一种摆杆式测流装置,通过量纲分析及理论推导得到流量与摆杆偏转角的半经验公式,并分析了其测流特性.王文娥等[10]、张维乐等[11]针对量水平板量水特性进行研究,提出了通过受力分析建立流量、水深、角度的理论关系式,以及利用闸孔出流公式拟合得到半经验公式这2种方法来建立流量计算模型.此类测流装置结构简单,携带方便,但仅能接收渠道中线上部分水流动能,量程受限.
针对目前中国量水方法中存在的量测精度低、影响渠道过流、价格昂贵、施工工艺复杂、测流不稳定等问题,设计了适用于斗农渠量水的弹簧板式测流装置,该装置结构简单、造价低、测流精度较高、携带应用方便.本研究在实验室模型试验的基础上,利用Fluent软件对该测流装置的水力特性进行数值模拟,并将其与模型试验结果进行对比分析;根据理论分析和量纲分析得到了统一形式的流量公式;综合分析不同板型弹簧板式测流装置的测流精度和水头损失,选定最优板型;对比分析该测流装置在不同量测板板宽条件下的测流特性.
1 试验设计
1.1 装置简介及测流原理
弹簧板式测流装置结构如图1所示,由图可以看到,该测流装置通过外壳上的支杆固定于渠道中,量测板因滑轨约束作用,受力后仅沿渠道纵向移动.量测导杆与量测壳体相连接置于量测套筒中.当量测板放入流动的水中时,会受到其运动方向上水流的绕流阻力作用,推动量测导杆挤压弹簧,与弹簧对量测板的弹力以及装置间存在的摩擦阻力达到平衡状态.

图1 弹簧板式测流装置轴测图
弹簧板式测流装置的量测板使渠道过流断面减小,阻碍了水流向下游传播,导致量测板上游水位壅高,动能转化为势能.水流在经过量测板时,势能转化为动能,流速增加.量测板为矩形平板,在板的侧边缘处产生边界层分离,并在下游回流至板下游面处,流态紊乱,造成能量损失.由于水流绕流产生的能量损失以及势能对动能的补偿作用,使板前后产生压差,对量测板形成推力.弹簧板式测流装置的测流原理是,利用水流绕流作用产生的压差阻力,推动量测板沿着滑轨方向水平运动,从而挤压弹簧,使水流推动量测板的力FR与弹簧弹力FK和装置间的摩擦力f达到平衡状态.在同一渠道同一坡度下,渠道断面瞬时流量大小不变,水流作用在量测板上的力也不变,即弹簧板式测流装置的弹簧形变量d也相同,渠道断面流量大小与弹簧形变量相对应.通过建立渠道过水断面瞬时流量与弹簧形变量的关系,在同一渠道下,得到弹簧形变量大小即可得到渠道瞬时流量.
1.2 试验方案
试验系统由地下水库、水泵、管道、电磁流量计、水箱、稳水板、矩形渠以及排水口组成,如图2所示.水泵从地下水库中抽水,通过管道输送至水箱中,水流由稳水板稳定后输往矩形渠,并由排水口将水排回地下水库,组成一套完整的地下水循环系统.试验中通过观察电磁流量计显示面板读数以及转动阀门来调节流量,观测量测套筒上的刻度获得弹簧形变量.
矩形渠宽度为270 mm,高320 mm,底坡1/1 000;弹簧参数为线径1 mm,中径20 mm,劲度系数0.119 5 N/mm;选取板宽分别为30,40,50,60 mm的矩形量测板;根据水泵性能选定流量为20~85 m3/h.量测板的淹没深度影响水流作用于量测板上的力,从而影响装置的量程.为尽可能地使量测板与渠道中线处水流完整接触,先将量测板安装于距渠底5 mm处,之后通过微调,在不影响量测板纵向移动的前提下,将板伸至紧贴渠底处.本试验每隔5 m3/h选取1个流量,共选取14个流量工况,利用精度为0.1 mm的游标卡尺测定4种不同板宽的量测板在不同流量情况下挤压弹簧产生的形变量.量测板上游水流平稳,在上游距离板0.2 m处选取控制断面1-1测量水位.
2 数值模拟
2.1 控制方程
以下是数值模拟计算过程中的控制方程[12]:
连续性方程为
(1)
动量方程为
(2)
式中:ρ为流体密度,1 000 kg/m3;Fbx,Fby,Fbz分别为单位质量流体上的质量力在3个方向上的分量,m/s2;pxx,pxy,pxz为流体内应力张量的分量,kg/s2·m;t为时间,s;u,v,ω分别为与x,y,z相对应的速度分量.
文中采用的模型为RNGk-ε模型,其湍动能k与耗散率ε的方程为
(3)
(4)
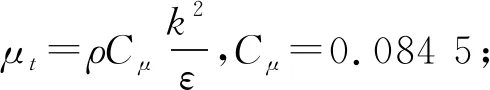
2.2 模型建立与网格划分
试验渠道宽270 mm,底坡1/1 000.数值模拟模型结构尺寸与试验渠道尺寸相同,且采用AutoCAD建立,并导入ANSYS-Meshing中划分网格.为研究量测板板宽变化对该装置量测特性的影响,分别建立30,40,50,60 mm这4种不同板宽的量测板模型.为模拟矩形渠道中水流真实流态,使水流在量测板上下游均趋于平稳,同时减少模拟时间,渠道模型长度选为7 m,量测板位于距渠道入口2 m,距渠底5 mm处,见图3.计算过程中,x轴正方向为水流方向,重力方向为y轴负方向,渠道横向为z轴方向.
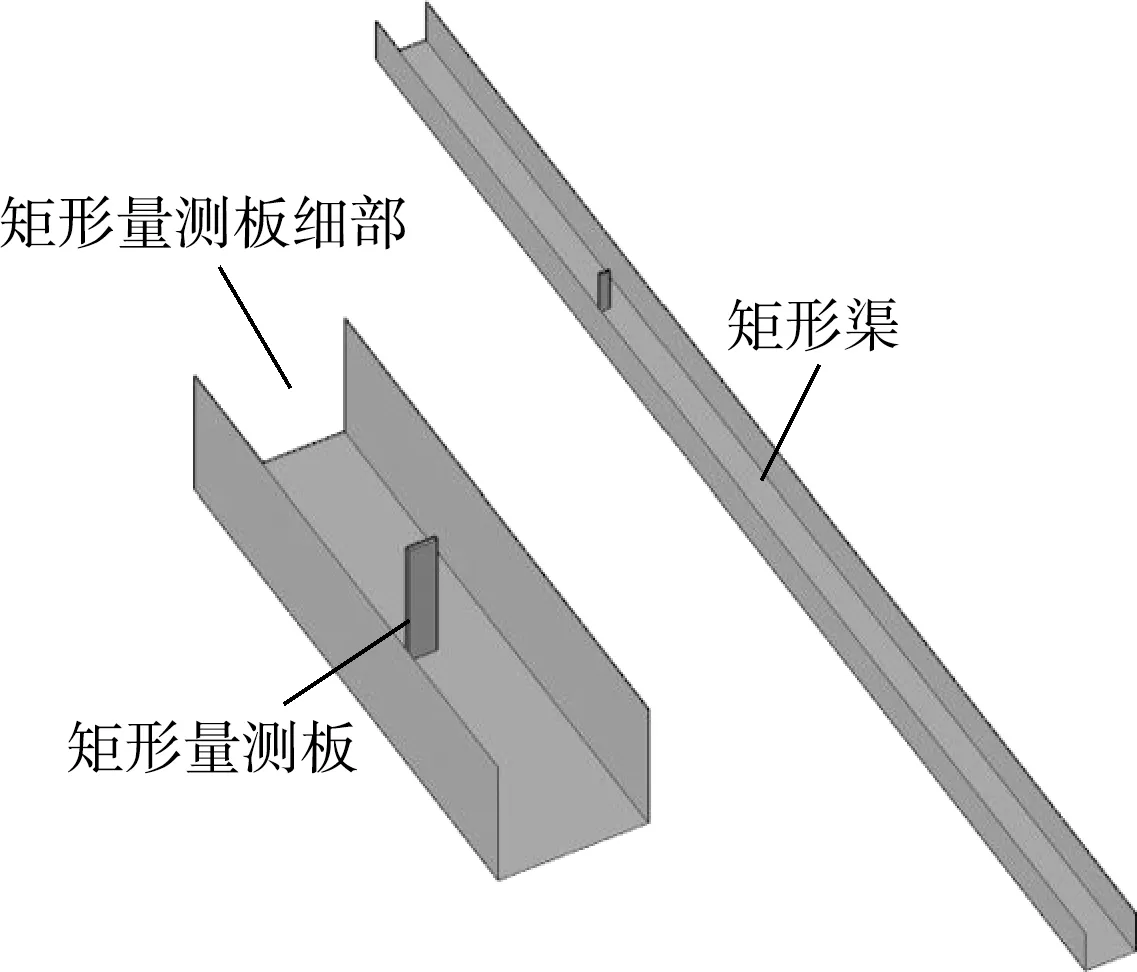
图3 简化计算模型
在流体计算求解前需要进行计算网格的划分,将空间连续的计算区域分割为足够小的计算区域,通过控制方程离散化并使用数值方法得到网格节点上的数据.本模型为量测板处于平衡状态时的模型,为保证计算精度,提高网格划分质量,网格划分尺寸为10 mm,划分总数为50万个.
2.3 网格无关性验证
在数值计算过程中,网格的大小和数量影响结果的精确性,为此通过监测不同网格大小下量测板上游水位变化对网格进行无关性检验,如表1所示,表中h为上游水位,B为量测板板宽.网格尺寸N为10,11,12,15 mm时上游水位的误差分别为0.26%,0.28%,0.18%,0.41%,网格尺寸对水位的影响均小于0.5%,满足数值模拟计算精度要求.因此采用网格尺寸为10 mm的计算模型开展计算.

表1 网格无关性检验
2.4 边界条件
明渠流动自由液面采用VOF模型,通过求解单独的动量方程及对穿过计算域的流体体积分数迭代计算,以模拟空气和水这2种不混合流体[13].
上游入口处分为水入口和空气入口,其中空气入口采用压力入口,水入口采用速度入口,水入口处水体积分数设置为1;渠道上表面为空气压力入口;出口处用压力出口;其他均为墙体,设置为无滑移边界条件,粗糙度常数为0.5;参考压强为大气压,整个流场中初始状态全部为空气,采用瞬态模拟[14].通过监测出口边界流量及量测板上压力的模拟结果,得到模型从初始时刻到计算稳定时间约为75 s,为了使模拟结果尽可能达到稳定状态,设置计算时长为105 s.
3 结果与分析
3.1 数值模拟可靠性验证
在研究明渠流动过程中,研究水面线可以很好地了解水流状态,通过数值模拟与实际流动对比分析,可以判断模拟的可行性.图4为量测板板宽为50 mm条件下,流量为50 m3/h时矩形渠道中模拟水面线变化图.试验观察发现,在不同板宽工况下(B=30,40,50,60 mm),水流进入渠道中水位逐渐升高并趋于稳定.量测板上游水流较为平稳,由于板的壅水,板前水位有所升高.量测板下游流态较为复杂,渠道中线水位先是急剧下降,然后急剧升高,同时渠道两侧水位急剧下降,下游水面上形成一个个浪峰,并且逐渐趋于平稳,与模拟结果相吻合.

图4 模拟流态图
距量测板上游0.2 m处选取断面,对量测板板宽分别为30,40,50,60 mm的弹簧板式测流装置在不同流量下水深的数值模拟结果hs与试验结果hm进行对比,如图5所示,从图中可以看出,随着板宽的增加,上游水深也在增加,这是因为量测板板宽的增加减小了渠道过水断面面积,量测板对水流的壅水作用变大,导致水深增加.实测上游水深的模拟值同试验值基本吻合:当板宽分别为30,40,50,60 mm时,上游水位最大相对误差分别为4.04%,3.55%,4.54%和4.10%,平均相对误差分别为1.77%,1.96%,3.00%和1.72%.上游水位相对误差值均小于5.00%,模拟结果符合实际,因此,采用Fluent软件对明渠弹簧板式测流装置进行模拟是可行的.
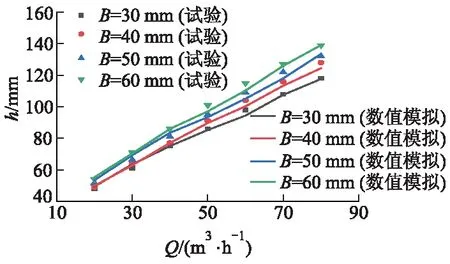
图5 实测水位与模拟水位对比
3.2 流量与形变量的关系
3.2.1 关系公式拟合
分析弹簧板式测流装置在测流过程中流量与弹簧形变量的关系是判断该测流装置是否可行的重要依据.图6为形变量d与流量Q的关系,由图可以看出,在同一板型下,弹簧形变量随着渠道断面流量的增大而增大.

图6 形变量与流量的关系
根据参考文献[11],弹簧板式测流装置的流量计算公式可以通过量纲分析法推导得出.试验和理论分析表明,影响弹簧板式测流装置量测流量Q的主要因素是重力加速度g、过水断面的水力半径R、水的密度ρw、水中的泥沙浓度S、水的动力黏滞系数μ、量测板的长度l、水流作用在量测板上的力FR(FR=kd+f,k为劲度系数,d为弹簧形变量.)、量测板的宽度B、量测板的厚度δ、渠道的糙率n以及渠道的坡度i.根据π定理及上述影响因素,写出函数关系为
f(Q,g,R,ρw,S,μ,l,FR,B,δ,n,i)=0,
(5)
由π定理得量纲为一的方程为
φ(π1,π2,π3,π4,π5,π6,π7,π8,π9)=
(6)
因此可以推导出
(7)
因此
(8)


又FR=kd+f,
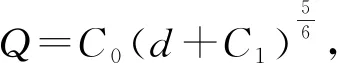
(9)

通过试验测得Q与d,利用线性拟合得到式(9)中的系数C0以及C1,如表2所示,表中E为均方根误差.可以看出,在矩形渠道中不同板宽下Q与d+C1的5/6次方线性相关性良好,确定系数均在0.99以上.
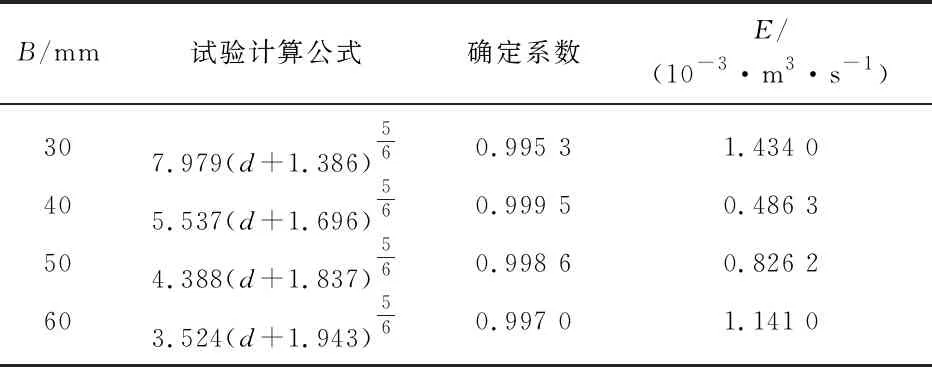
表2 公式拟合
3.2.2 量测精度分析
将试验测得的形变量d代入表2公式中,可得4种不同板宽弹簧板式测流装置的公式计算流量.对公式计算流量和试验时的实测流量进行误差分析,误差计算公式为
(10)
式中:e为测流相对误差;Qc为计算流量,m3/h;Qm为实测流量,m3/h.
由计算可知,在矩形渠道中,弹簧板式测流装置计算流量和实测流量的关系如图7所示.在量测板板宽分别为30,40,50,60 mm时,最大相对误差分别为4.41%,1.43%,4.56%和4.28%,平均相对误差分别为2.02%,0.88%,1.40%以及1.79%.结果表明,弹簧板式测流装置的量测板板宽不同时,计算流量与实测流量之间存在的相对误差均小于5%,量测精度较高,满足灌区量水要求.

图7 计算流量与实测流量对比
3.3 水头损失及板型选择
3.3.1 水头损失
灌区量水过程中,因量水设施而产生的局部水头损失会直接影响灌溉效率,因此需要对量水设施产生的水头损失进行研究.弹簧板式测流装置应用过程中渠道水流产生的水头损失,一方面是水流的黏滞力作用而产生的沿程水头损失;另一方面则是当水流到达量测板位置时,因量测板对渠道的收缩作用导致过水断面在量测板位置突然缩小,水流由缓流过渡为急流,因惯性作用与量测板边界分离,产生旋涡,造成水流紊动加剧,水分子质点相互碰撞产生能量耗散,从而产生局部水头损失.
在坡度为1/1 000的矩形渠道中,从下游稳定水面处选取控制断面2-2,对不同板宽的弹簧板式测流装置测流过程中产生的水头损失进行分析.根据能量方程,可推知水头损失公式
(11)
式中:hj为水头损失,m;h1为断面1-1水深,m;h2为断面2-2水深,m;v1为断面1-1平均流速,m/s;v2为断面2-2平均流速,m/s;α1,α2为动能修正系数,α1=α2=1;g为重力加速度,m/s2.
图8为不同极宽量测板水头损失,图中G为测流装置造成的水头损失hj占上游总水头的百分比.由图可以看出,板宽为50,60 mm时的最大水头损失比均在10%以上,板宽为30,40 mm时的最大水头损失比均在10%以内.在同一流量下,随着板宽的增加,水头损失也在增加.
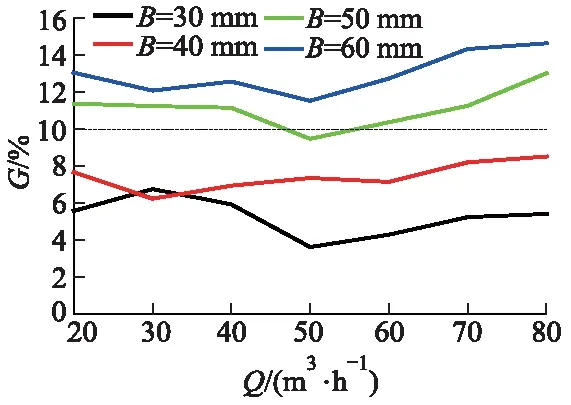
图8 不同板宽量测板水头损失
3.3.2 板型选择
在同一流量下,随着量测板的淹没深度减小,底边缘高程抬升,对渠道断面的收缩作用减小,使水流更容易向下游传播,从而造成上游壅水高度降低即水面高程降低,水流与板的接触面积减小,作用于板上的推力减小,弹簧形变量减小,文中装置的量程对应降低.因此,装置在使用过程中需将量测板伸至渠底处,使该装置拥有最大的量程范围.
由图7可以看出,弹簧板式测流装置在板宽为40 mm时的量测精度最高,30 mm时的量测精度最低.根据Hooke定律和机械摩擦理论可知,弹簧板式测流装置在流量很小时,因摩擦作用装置间的摩擦力与水流作用在量测板上的推力达到平衡,此时弹簧不发生形变,该装置存在量程下限.由表2中的公式可以看到,随着板宽的减小,该测流装置的量程下限在增加,30 mm时量程下限最大,所能测得的最小流量为10.5 m3/h.对图8中不同板宽的量测板产生的水头损失对比分析得知,板宽增加的同时水头损失也在增加,大于50 mm时的水头损失占比均大于10%,且板宽增大也不利于渠道中漂浮物的通过.在满足测流精度、保证装置量程的前提下,为尽可能降低水头损失,选取板宽为40 mm的量测板.该量测板最大测流误差为1.43%,最大水头损失比在10%以内,满足使用要求.
4 结 论
1) 对量纲分析得到的计算模型中的待定系数进行拟合,得到了具有统一形式的流量计算公式.同一弹簧参数下,随着量测板板宽的减小,弹簧板式测流装置测流范围也减小.对比分析流量计算值和实测值可以看到,计算流量和实测流量最大相对误差为4.56%,其中板宽为40 mm时误差最小,最大相对误差仅为1.43%,满足灌区量水需求.
2) 利用Fluent中VOF模型和RNGk-ε湍流模型对矩形渠道中水流特性进行模拟研究是可行的,模拟渠道水深与实测水深最大相对误差为4.54%,水面线变化情况与实际相符.
3) 随着量测板板宽的增加,水头损失也在增加,其中板宽为50,60 mm时的水头损失均在10%以上,其余板型均小于10%.
4) 基于量程、水头损失和测流精度选取了板宽为40 mm的量测板为最适宜的量测板.

