基于PFC2d的平行粘结模型宏-细观参数标定研究

汪 洋， 孟祥林， 高 进， 郭治岳

(1.成都建工路桥建设有限公司，四川成都，610000；2.西南交通大学土木工程学院，四川成都，610031)

在利用离散元模型来进行数值模拟时，颗粒间的每个接触模型都有多个细观参数，在选用颗粒间的接触模型时，往往需要定义较多的细观参数，为了使颗粒集合体所呈现出的宏观力学性质与其模拟的土石材料相接近，对细观参数对宏观参数的影响进行研究，并利用影响规律进行宏-细观参数的标定是非常重要的。

国内有许多学者针对离散元软件的宏-细观参数影响及参数标定进行了研究。赵国彦等[1]采用理论分析与数值模拟结合的手段，对平行粘结模型中细观参数对宏观特性进行了系统性研究，定量给出了部分细观参数与宏观参数的关系式；刘畅等[2]通过PFC2d建立岩石材料的单元试验数值模拟，总结了部分细观参数与宏观参数的关系；阿比尔的等[3]采用控制变量法，较为全面的分析了各细观参数与宏观参数间的定量关系，并考虑参数相互影响，拟合了经验公式，对细观参数选择进行了优化；郝保钦等[4]采用多因素方差分析法确定了平行黏结模型中细观参数对宏观力学参数的影响程度并建立了参数关系式，提出了岩石弹性模量、泊松比单轴抗压强度等宏观力学参数的细观参数确定方法。综上所述，如何对岩体材料的细观参数与宏观力学参数进行标定值得深入探讨，为了更好地利用给定岩体宏观参数匹配出响应细观参数，本文利用PFC2d离散元软件，基于单轴压缩试验和双轴压缩试验，通过敏感新分析得到了优化的宏-细观参数标定流程，并进行标定验证，对准确、高效地进行参数标定具有指导作用。

1 平行黏结模型

利用离散元软件进行数值模拟时，不需要设置岩体的宏观力学参数，可针对颗粒选择合适的接触模型即反映岩体的宏观力学特性。本文触模型选用平行黏结模型，因其具有能够同时传递力和力矩的特点，可以更好地体现完整岩体的力学特性。

基于平行黏结模型，选取emod、krat、pb_emod、pb_krat、pb_ten、pb_coh、pb_fa和fric 8个细观参数，建立室内单轴压缩试验和双轴压缩试验进行数值模拟，考虑岩体的弹性模量、泊松比、内摩擦角和粘聚力，对岩体材料宏-细观参数的影响规律进行研究并进行参数标定。

2 抗剪强度参数计算

针对多组双轴试验数据，抗剪强度参数计算目前最常用的回归方法为“p-q”法和“σ1-σ3”法[5]。

“p-q”法，是一种间接现行回归方法，在p-q坐标内进行先行回归(即纵坐标和横坐标分别为p和q)，利用最小二乘法进行线性回归，求得拟合方程的斜率和截距，然后根据式(1)～式(4)可求得抗剪强度参数：

(1)

(2)

f1=tanφ=tan(arcsin(tanα))

(3)

c1=a/cos(arcsin(tanα))

(4)

式中：σ1为峰值应力；σ3为围压；a为“p-q”法拟合方程截距；α为“p-q”法拟合方程夹角。

“σ1-σ3”法，是一种直接回归方法，由于试验中直接测试得到的为σ1和σ3，因此用该方法回归更为直接，相关计算公式如式(5)～式(7)所示：

σ1=2ctan(φ/2+π/4)=σ3tan2(φ/2+π/4)

(5)

f2=tanφ=tan(2arctanB0.5-π/2)

(6)

c2=A/(tan(φ/2+π/4))

(7)

式中：A-σ1-σ3法截距，取2ctan(φ/2+π/4)；B-回σ1-σ3法斜率，取tan2(φ/2+π/4)。

利用上述2种方法求得抗剪强度参数后，取平均值作为最终强度参数，公式如式(8)～式(9)所示：

f=f1+f2

(8)

c=c1+c2

(9)

式中：f为最终摩擦系数；c为最终粘聚力。

3 数值模拟

3.1 单轴压缩试验

单轴压缩试验又被成为无侧限压力试验，是对圆柱形土样不加侧向压力，而只在中心轴线上逐步加垂直压力，直到土样破坏为止的试验。模型尺度为50 mm×100 mm，最小粒径取模型直径的1/80，粒径比设置为1.66。为保证单轴压缩试验的真实性，数值模拟从取土、制作土样、土体物理力学性质等方面缩小与实际试验的差距，对试样进行预压模拟土体原来的储存状态，考虑岩体埋深区间，按照岩体处于地下50 m进行预压，预压值为1 MPa，对土体进行卸载模拟取土后的储存状态。单轴试验数值模型及模拟过程见图 1。

图1 单轴压缩试验

3.2 三轴压缩试验

双轴压缩试验是目前研究土样抗剪强度较为完善的方法，在进行试验时，先加液压即通过把压力水通入盛土样的压力室，使土样在横向受到相等的压力，即为施加“围压”，然后维持液压不变，在试样轴向施加垂直压力并不断增大，直到土样被压坏。模型尺度为50 mm×100 mm，最小粒径取模型直径的1/80，粒径比设置为1.66。为保证单轴压缩试验的真实性，数值模拟从取土、制作土样、土体物理力学性质等方面缩小与实际试验的差距，对试样进行预压模拟土体原来的储存状态，预压值设为1 MPa。由于双轴压缩试验至少需要进行3组才可得到有效的土样抗剪强度指标，选取围压为2 MPa、3 MPa和4 MPa进行试验。双轴试验数值模型及模拟过程见图 2。

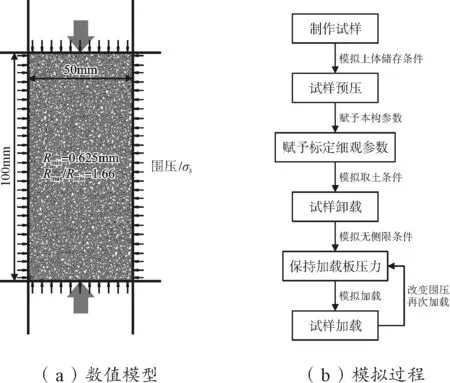
图2 双轴压缩试验

4 敏感性分析

PB设计试验能通过各因素的2个水平的差异与整体的差异进行比较来确定各影响因素的显著性，并可以对各因素进行敏感性排序，筛选出具有显著影响的因素，避免试验资源的浪费，从而减少不必要的工作量，有助于标定工作的准确性。

本次PB设计试验中平行粘结模型中各细观参数设置为两水平，由于有8组细观参数，在设置设计矩阵时，选取N=16的设计矩阵开展试验，试验设计矩阵及试验结果见表 1。

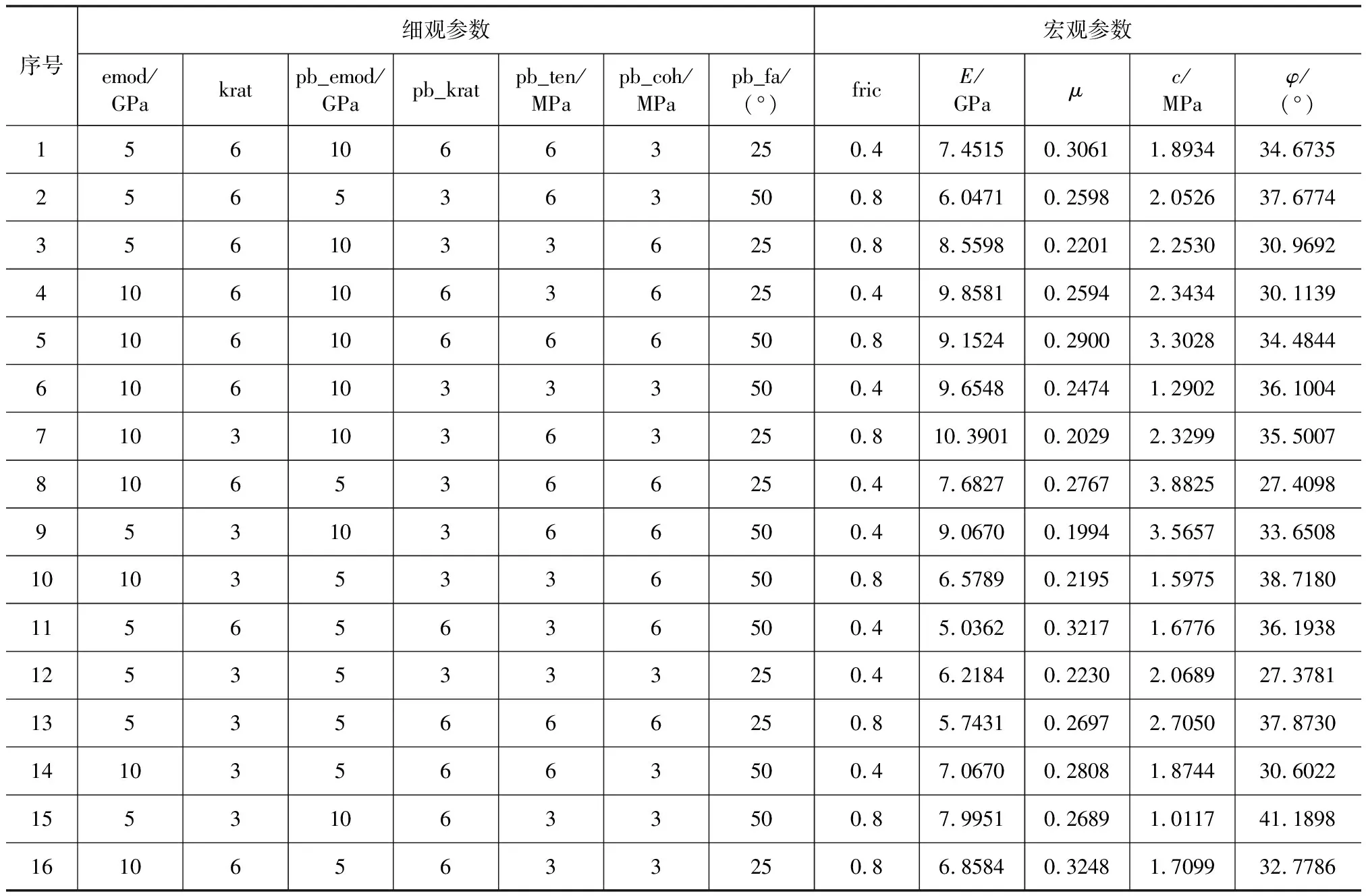
表1 设计矩阵及试验结果

标准化效应图可反映影响因素的敏感性大小，原理为对各影响因素进行检验，并将获得的效应值的绝对值作为比较指标，按其大小进行排序，并与显著性水水平所计算得出的显著性临界值进行比较，该大小可作为其敏感性排序的依据，效应值越大，越敏感。将上述结果代入计算软件中，对结果进行因素设计分析，基于16组试验结果的各宏观参数的标准化效应图见图3。

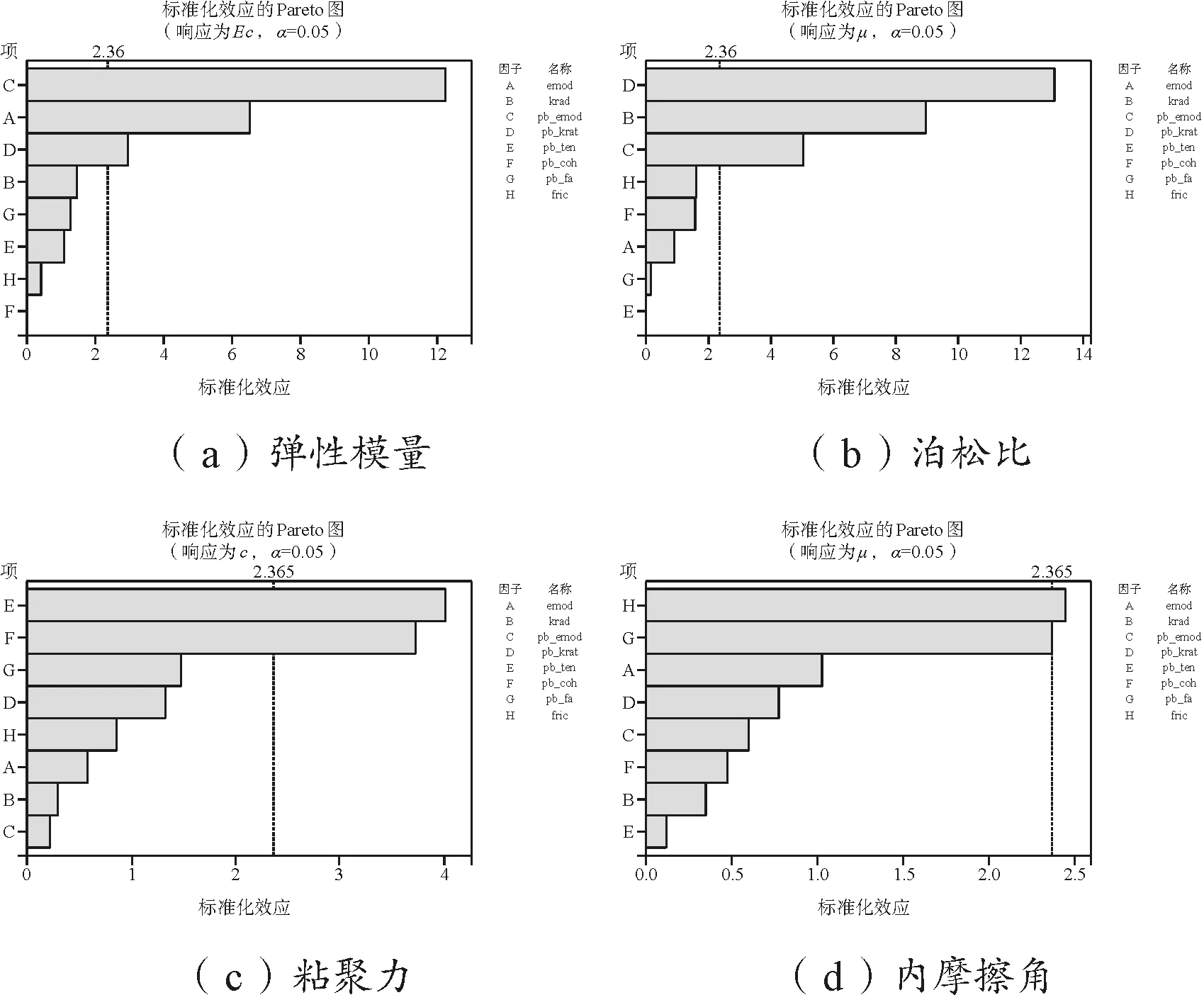
图3 各宏观参数的标准化效应图

由图3可知：对宏观参数弹性模量影响显著的因素为pb_emod、emod和pb_krat；对宏观参数泊松比影响显著的因素为pb_krat、krat和pb_emod；对宏观参数粘聚力影响显著的因素为pb_ten和pb_coh；对宏观参数内摩擦角影响显著的因素为fric和pb_fa。

5 实例验证

敏感性分析为宏-细观参数标定指明了基本流程。通过敏感性分析结果可以在进行参数标定时对细观参数调整有更为定量的把控。基于“粗调”与“微调”相结合的原则，针对与目标宏观参数的差距合理调整细观参数。标定流程见图4。

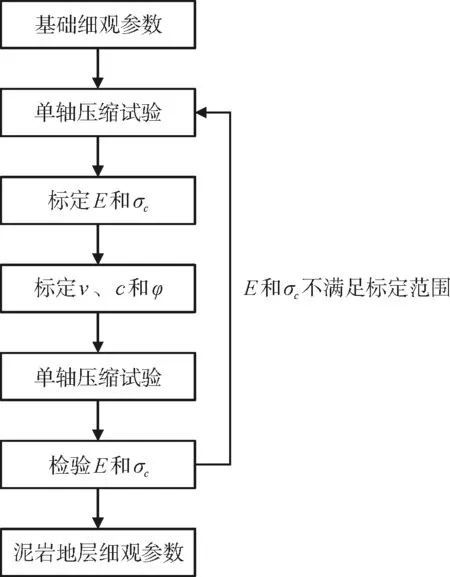
图4 标定流程

本文选取四川成都龙泉山隧道附近围岩参数，见表 2。考虑到细观参数较多且试验过程中的误差性，标定后的细观参数反映的宏观参数在标定值的90%～110%范围内即可认定为符合标定要求。

表2 现场围岩参数

按照标定流程，对围岩参数进行标定，单轴压缩试验与双轴压缩试验的模型尺寸与模拟流程见本文第3节，标定结果见表 3。

表3 标定结果

选用标定结果对试验进行单轴压缩试验可得到单轴试验的应力应变曲线见图 5。从应力应变曲线中可直观的得到单轴抗压强度为1.32 MPa；弹性模量为曲线中直线段终点的应力差与对应的应变差的比值[6]，该组数据得到的应力应变曲线上升段较为平稳，因此用应力峰值与开始加载时的应力差值比应变差值即为弹性模量为2.69 GPa。

图5 单轴压缩试验-应力应变曲线

利用双轴压缩试验可得到不同围压下的应力应变曲线见图 6，试样在2 MPa、3 MPa和4 MPa下的峰值应力分别为8.91 MPa、12.03 MPa和15.37 MPa。

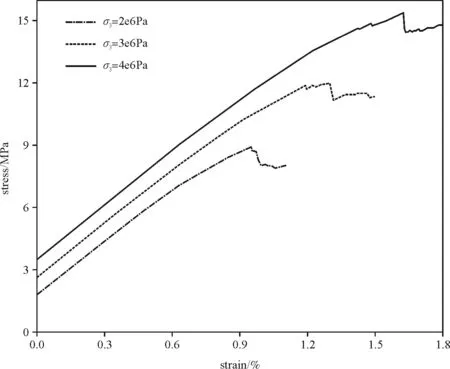
图6 双轴压缩试验-应力应变曲线

提取试验的横向应变-轴向应变曲线见图7，可发现不同围压下的曲线的变化规律相似，均经历一段线性增长后加速增长，围压越大增长速率越慢，通过线性阶段的数据可求得试样的泊松比为0.285。

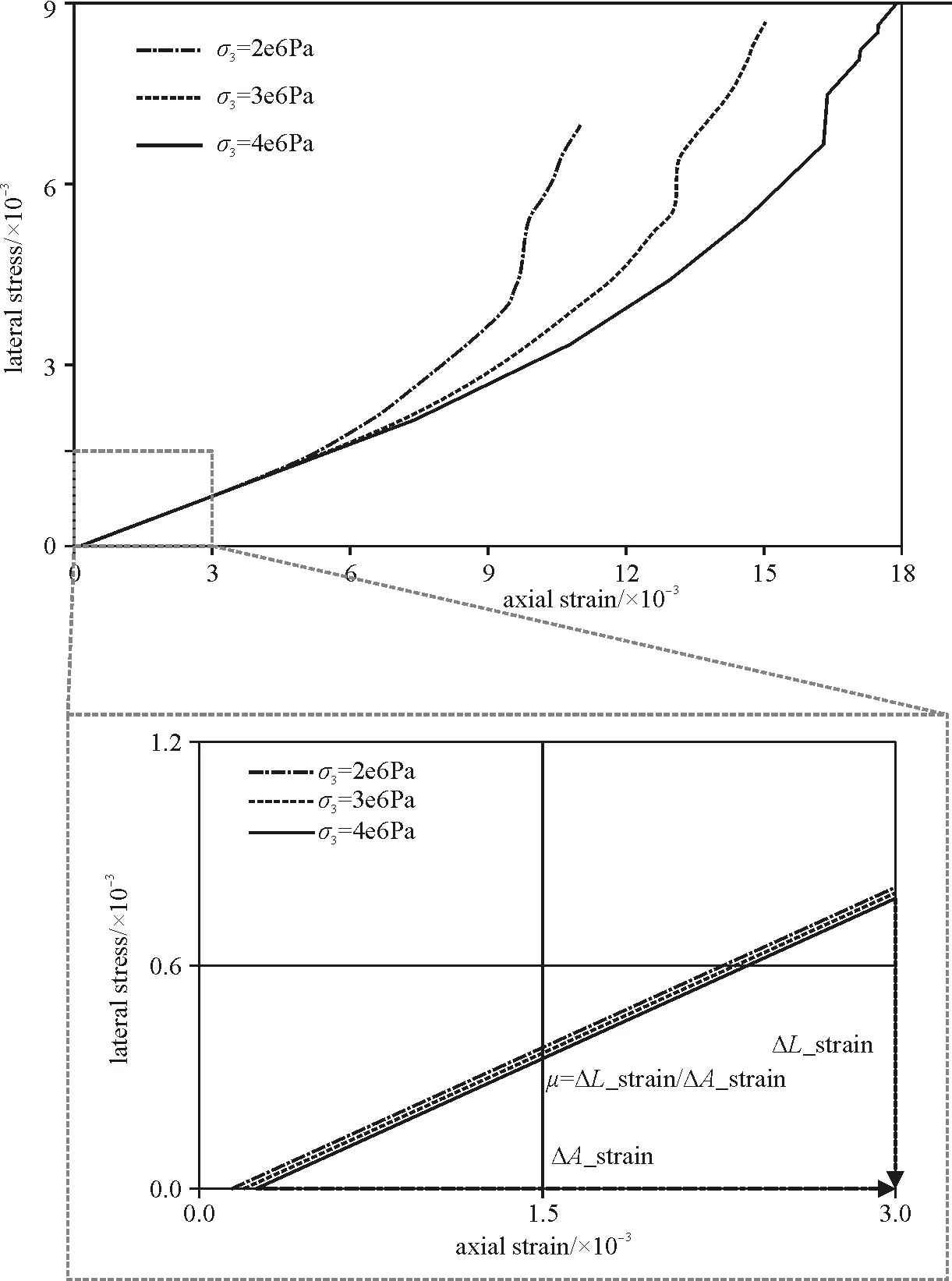
图7 横向应变-轴向应变曲线

通过“p-q”法和“σ1-σ3法”法计算得到的岩石抗剪强度参数见表4，取2种方法的平均值，求得岩石粘聚力为0.670 MPa，内摩擦角为31.85°。

表4 抗剪强度参数计算结果

6 结论

本文基于PFC2d离散元软件中的平行黏结模型，选取emod、krat、pb_emod、pb_krat、pb_ten、pb_coh、pb_fa和fric 8个细观参数，考虑岩体的弹性模量、泊松比、内摩擦角和粘聚力，研究了岩体材料宏-细观参数的相互影响关系，得到结论：

(1)总结分析了双轴压缩试验中抗剪强度参数的计算方法，确定了以“p-q”法和“σ1-σ3法”法计算得到的抗剪强度参数取平均即为最终抗剪强度参数。

(2)建立考虑原状土、取土和制作土样不同储存条件的单轴压缩试验和双轴压缩试验进行数值模拟，最大程度的缩小与实际试验的差距。

(3)选取N=16的设计矩阵开展PB设计试验，对8个细观参数在两水平条件下进行敏感性分析，得到弹性模量的显著因素为pb_emod、emod和pb_krat；泊松比为pb_krat、krat和pb_emod；粘聚力为pb_ten和pb_coh；内摩擦角为fric和pb_fa。

(4)确定了细观参数的标定流程并采用该流程对龙泉山围岩进行参数标定，基于应力应变曲线、横向应变-轴向应变曲线完整计算了宏观参数，验证了参数标定流程的可行性。