均质土坡边坡稳定性敏感性分析

张小波

(中南勘察设计院集团有限公司，湖北武汉 430070)

随着工程技术的快速发展，边坡工程受到越来越多人的关注。实际工程中，由于不同边坡土体的影响因素不尽相同，因而，对边坡稳定性的影响性因素的探究从未止步。

边坡稳定性是边坡工程的核心内容之一，其中重点是对边坡稳定性的敏感性因素分析。边坡稳定性的敏感性因素的分析主要是通过分析边坡稳定性因素与边坡稳定性的关系来确定。在实际的研究中，边坡稳定性常用强度折减法与灰色关联理论的结合来分析说明。Zienkiewicz等[1]在研究理想粘塑性模型关联和非关联形式力学行为在土力学中的应用时引入了强度折减系数的概念，此后由Matsul等[2]命名为强度折减法。边坡的安全系数是通过强度折减法计算出的临界破坏折减系数。灰色关联理论是对边坡稳定性分析的最佳理论，其避开了传统分析方法分析过程中的复杂性和可变性，能够准确的找到影响边坡稳定的最敏感因素，有助于工程针对性的对边坡滑坡预防、治理采取措施，有助于防止边坡失稳破坏及边坡施工设计。目前，许多学者利用灰色关联理论分析边坡稳定性，牛岩等[3]基于灰色关联理论对用有限元法得到的结果建立数学模型，以此分析了边坡稳定性的各种因素，确定了粘聚力是影响边坡稳定性的最敏感因素，陈志波等[4]认为土体的物理力学参数c、φ是影响边坡稳定性的主要因素，牛越先等[5]通过灰色关系理论分析了坡高、坡度、c、φ对边坡稳定性的影响，发现c、φ和坡高对边坡稳定性影响比较难敏感，井培登等[6]以一土质边坡为例，选取容重、粘聚力、内摩擦角及坡角、坡高等5个影响边坡稳定性因素，利用灰色关联理论对其进行敏感性分析，结果表明，粘聚力和内摩擦角是影响边坡稳定性的主要因素，Luo[7]则通过计算重力、粘聚力、内摩擦角和孔隙水压力等因素对边坡稳定性的影响研究，找出了影响边坡稳定性的最敏感因素，为边坡稳定性敏感性分析提供了一种新方法，Xuemei等[8]以重度、粘聚力、内摩擦角、地下水位和坡比为试验因素，采用单因素分析方法进行敏感性因素分析，表明坡比是影响稳定性的最敏感因素，而内摩擦角和粘聚力次之。由研究可知，不同的研究会得出不一样的研究结果，但主要集中在边坡土体的粘聚力、内摩擦角、坡度及坡高4个因素。为探究不同因素对边坡稳定性的影响大小，常借助灰色关联分析法可以快捷的分析计算各种因素对边坡稳定性影响程度，确定影响边坡稳定性的最敏感因素。

综上所述，本文结合实际的工程经验，为求得影响边坡稳定性的最敏感因素，对一均质土边坡进行了建模，并对其稳定性进行计算与分析。首先，利用Midas GTS数值软件对均质土边坡进行建模；其次，将模型导入FLAC3D中采用强度折减法对20个不同工况下的边坡进行稳定性计算；然后，采用灰色关联理论来分析数值模拟结果，得到影响边坡稳定性因素的灰色关联系数及灰色关联度，从而确定了影响边坡稳定性因素敏感性大小，确定了边坡稳定性的最敏感因素，为边坡的施工设计提供理论支持。

1 研究方法与理论

1.1 强度折减法

边坡岩土体抗剪强度的确定需要使用强度折减法的折减计算得到，将岩土体的抗剪强度参数粘聚力c和内摩擦角φ按照式(1)和式(2)进行不断的折减，当抗剪强度刚好达到临界破坏状态时，可获得新的抗剪强度参数c′、φ′。然后将新得到的抗剪强度参数继续折减，重复计算操作，直到岩土体达到临界破坏状态，以得到此时的折减系数即为安全系数。

(1)

(2)

式中：c、φ和c′、φ′分别为岩土体材料实际的粘结力、内摩擦角和折减后的粘结力、内摩擦角，f为折减系数。

1.2 灰色关联理论

灰色关联分析是灰色系统理论[9]的一个部分，其是分析各关联因素关系的一种系统分析方法，弥补了回归分析、方差分析等需要大量原始数据的数理统计分析方法的不足。运用灰色关联分析方法的目的是找出边坡土体影响因素的主次关系，以确定影响目标的主要因素。

首先以影响边坡稳定性的各因素(粘聚力、内摩擦角、坡度及坡高等)为比较列X，X=[X1,X2…Xn]T，边坡安全系数作为参考列Y，Y=[Y1,Y2…Ym]T，分别列出X，Y的矩阵形式，如式(3)、式(4)所示。

(3)

(4)

考虑到比较列X和参考列Y内各数据可能因为量纲不同而无法得出正确的结果，因此，对数据进行转换处理，即对矩阵进行无量纲化转换，使其能够进行比较。式(3)和式(4)处理后得到式(5)～式(7)。

(5)

(6)

Δij=|xij′-yij′|

(7)

式中：

灰色关联分析的实质是分析曲线间几何形状的差别大小，线差值的大小，就是曲线间几何形状关联程度的大小，找出各个比较点与参考点之间的距离，通过分析找出各因素的相关性和差异性。比较因素和参考因素的相关性用关联系数来反映，关联系数的公式(8)为：

(8)

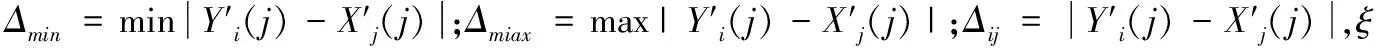
由于关联系数的个数较多且较分散，不便于比较，常用各相关因素的平均值作为其关联度来进行比较，关联度的值在[0，1]之间，关联度的值越大，说明该因素对目前对象的影响越大，即其敏感性越大，通过比较各个因素的关联度大小，得到各关联度的排序，进而得到影响目标对象排序，从而得到影响因素的主要因素与次要因素。关联度的求取公式(9)为：

(9)

2 模型的建立与分析

首先，边坡网格模型的建立是在Midas GTS软件实现的。然后，将得到的网格模型导入FLAC3D软件，设置边坡网格模型边界约束条件为：限制模型左侧边界单元的x方向位移，限制模型右侧边界单元的x方向位移，限制模型底部单元的x、y、z3个方向的位移，并施加重力条件，无动荷载，采用强度折减法进行稳定性分析计算，边坡数值模型如图1所示。

图1 边坡数值模型

2.1 数值模型工况的设置

影响边坡稳定性重要的4个因素是边坡土体的粘聚力c、内摩擦角φ、坡度h及坡高θ。为此，本文对不同工况下边坡土体建立了数值模型，探究不同工况下的边坡稳定性，工况设置如表1～表4所示。

表1 粘聚力设计方案

表2 内摩擦角设计方案

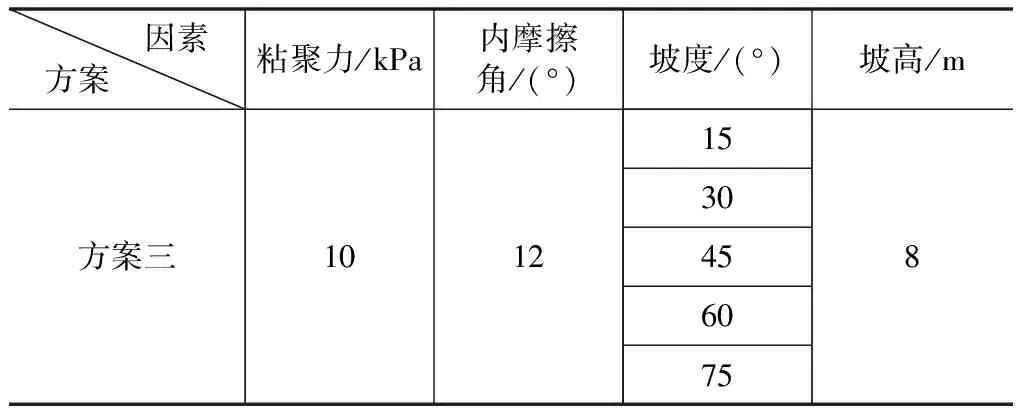
表3 坡度设计方案

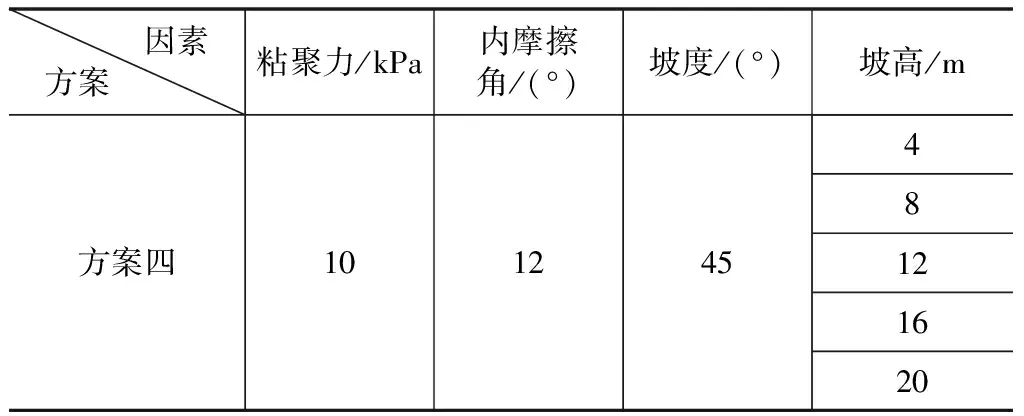
表4 坡高设计方案

2.2 敏感性因素分析

对应不同工况下边坡安全系数Fs的计算结果如表5～表8所示。

由表5～表8数据可知，随着边坡土体的粘聚力和内摩擦角的增大，边坡的安全系数也随着增大，而边坡的安全系数随着坡度与坡高的增大而减小。在边坡工程中要关注边坡土体的物理力学参数及边坡的坡度、坡高对边坡稳定性的影响，减小边坡发生失稳破坏的可能。

表5 Fs随粘聚力c值变化值

表6 Fs随内摩擦角φ值变化值

表7 Fs随坡度θ变化值

表8 Fs随坡高h值变化值

将各因素变化值作为比较列X，边坡安全系数作为参考列Y，建立比较矩阵和参考矩阵：

利用式(5)～式(7)对比较列矩阵X和参考列矩阵Y进行无量纲化处理得到矩阵△：

通过式(8)得到关联系数矩阵γ：

由此可得关联矩阵G：

由此可知，影响边坡稳定性因素敏感性大小为：粘聚力c>内摩擦角φ>坡高h>坡度θ，则影响边坡稳定最敏感因素为边坡土体粘聚力，边坡土体的物理力学指标c、φ对边坡稳定性影响程度最大，是影响边坡稳定性的主要因素。

3 结论

通过Midas GTS、FLAC3D数值模拟软件对均质土边坡进行建模计算分析边坡稳定性，结合灰色关联分析理论，对影响均质土边坡稳定性因素进行敏感性分析，得到了结论：

(1)边坡的安全系数随着边坡土体的粘聚力、内摩擦角的增大而增大，随着坡度、坡高的增大而减小。在边坡设计过程中要注意这些参数的变化，减小边坡发生失稳破坏的可能。

(2)影响边坡稳定性因素敏感性大小为：粘聚力c>内摩擦角φ>坡高h>坡度θ，影响边坡稳定最敏感因素为边坡土体粘聚力，边坡土体的物理力学指标c、φ对边坡稳定性影响程度最大，是影响边坡稳定性的主要因素。

(3)通过折减法与灰色关联分析的结合使用，可以高效、便捷的反应各因素对边坡稳定性影响程度，确定影响边坡稳定性的最敏感因素，为边坡的建设和防护提供理论支持。