管幕冻结隧道“顶管-冻土”复合结构力学特性试验研究

段 寅，荣传新，蔡海兵，龙 伟

(1.深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001；2.安徽理工大学 土木建筑学院，安徽 淮南 232001)

在大量人工地层冻结工程中，往往将冻土作为主要承载结构[1]，对其冻结温度、冻土帷幕厚度与强度等进行设计研究。而冻结器作为供冷部件，其主要研究内容为如何避免在冻结过程中发生断裂破坏以及冻结液泄漏等[2-3]，也有部分学者针对其力学特性开展试验研究[4-6]。日本学者[7-8]曾针对由冻结砂土和钢管组成的复合结构梁进行过承载力试验，证明复合结构梁的破坏荷载在不同冻结温度下相对“纯冻土梁”能提升2～5 倍，同时指出不同土性下复合结构的承载力各不相同。夏慧民[9]、李志军[10]等也曾对加筋(钢筋或冻结器)人工冻土梁的“荷载-位移”关系进行探究，得出冻土构件内冻结器(钢筋)的加筋作用主要体现为构件整体刚度和抵抗破坏荷载能力两方面的增强。上述研究成果大多源于管棚冻结法中的“管棚+冻土”复合结构，其主要特征为管棚钢管直径范围[11-13]一般为79～299 mm，管棚间距[14]一般为100～300 mm，管径与管间距相当或小于管间距。同时管棚冻结所形成的冻土尺寸远大于管径，复合结构中仍以冻土作为主要承载体。

港珠澳大桥拱北隧道暗挖段工程在国内外首次成功应用管幕冻结施工技术[15-17]。该技术综合了管幕法和人工地层冻结法的优势，首先在隧道开挖断面外围预先顶进大直径密排钢制顶管(18 根实顶管和18 根空顶管交替排布)以形成管幕，再通过顶管内置的两类冻结器(圆形冻结器和异形冻结器)冻结管间土层，最终构成“顶管-冻土帷幕”复合支护体系[18-20]。有效实现了“承载”与“顶管间止水”的双重目标，确保了隧道断面在开挖时周边环境的稳定与安全。

近年来，国内学者在管幕冻结法的施工方案[21-22]、冻结控制技术[23-24]、顶管顶进技术[25]、开挖支护方法[26-27]和施工监测[28]等方面进行了诸多研究和论证，为该法的应用和推广提供了坚实的基础。但管幕冻结法在设计理念和受力机理上与管棚冻结法存在显著区别。首先顶管代替冻土作为主要承载体，其管径(1 600 mm)远大于管间距(平均335 mm)；其次顶管间的冻土帷幕厚度尺寸受到地表冻胀融沉量的严格限制，仅为管径的1～2 倍；第三是采用实顶管(顶管内填充混凝土)和空顶管的“空-实”顶管交替间隔布置的形式，相邻顶管存在刚度差异，所形成的“顶管-冻土”复合结构在荷载作用下会存在差异变形。特别是复合结构在形成过程中顶管、冻土和温度场之间的相互作用关系，以及承载阶段的结构受力、变形和破坏特征，已有研究成果尚未对此重点关注。

因此，为更好地了解该复合结构的力学特性，笔者结合实际工程背景和研究经验[29-30]，自主研发一套大型“顶管-冻土”复合结构物理模型试验系统，对复合结构形成过程中的温度场分布规律、土体冻胀变形及其荷载-位移关系、顶管受力与变形等因素进行分析，以期为管幕冻结技术的推广提供参考。

1 模型试验设计

1.1 试验对象与条件简化

如图1 所示，港珠澳大桥拱北隧道暗挖段工程原型中的管幕与冻土帷幕形态较为复杂，本文主要以“顶管-冻土”复合结构形成过程及其力学特性为研究内容，因此选取原型中1 号实顶管、2 号空顶管及其周围冻土作为模型试验对象，如图2 所示，并结合试验条件进行以下简化。

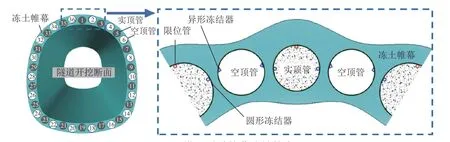
图1 拱北隧道管幕冻结技术Fig.1 Freeze-sealing pipe roof method for Gongbei tunnel

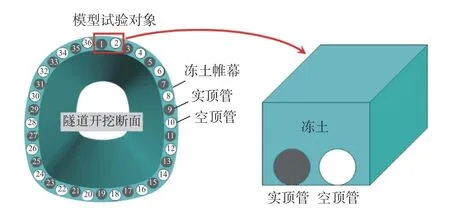
图2 模型试验研究对象Fig.2 Research object of model test

(1) 忽略原型中顶管的纵向曲率、相邻顶管间的错位角等，在试验中采用水平直线布管方式。

(2) 简化原型中两类冻结器的开启时序以及限位管的影响，在试验中仅考虑冻结器同时开启的情况。

(3) 从原型诸多土层中选取一种具有代表性的粉质黏土作为试验土层并进行重制。

(4) 原型中1 号实顶管、2 号空顶管及其周围冻土所形成的复合结构主要承受上部覆土荷载，在模型试验中将其转化为梁的受力模型，并结合试验条件确定加载方式。

1.2 相似准则与试验材料

采用量纲分析法[31]，以温度[θ]、时间[T]、长度[L]和力[F]为基本量纲，选取试验主要影响参数如下：

(1) 土体参数。含水率w(%)、弹性模量Et(N/m2)、黏聚力c(N/m2)、内摩擦角φ(°)、容重γt(N/m3)、应力σ(N/m2)、荷载P(N)、导温系数at(m2/s)、比热容Ct(J/kg·℃)、温度t(℃)。

(2) 顶管参数。弹性模量Eg(N/m2)、容重γg(N/m3)、直径D(m)、导温系数ag(m2/s)。

(3) 实顶管内混凝土参数。弹性模量Eh(N/m2)、容重γh(N/m3)。

(4) 冻结器参数。直径d(m)、管壁温度td(℃)。

基于Buckinghan 定理，共推导得到12 个相似准则(π1-π12)，见表1。结合原型结构特征与试验设备条件，首先确定几何相似比Cl=1/20；根据表1 推导出主要相似比常数见表2；根据几何相似比得到钢顶管设计参数和外形见表3，如图3 所示。试验土体采用粉质黏土，按原型的密度、含水率等进行重制，经室内实验[32-33]得到土样热物理和力学参数分别见表4 和表5，且经多次试验表明，冻土的强度和弹性模量随着温度的降低均呈线性增大。实顶管内充填的C30 细石混凝土，经实验[34-35]得到材料参数见表4。

表1 相似准则Table 1 Similarity criteria

表2 主要相似比常数Table 2 Main similarity ratio constant

表3 顶管设计参数Table 3 Design parameters of jacked pipe

表4 粉质黏土与混凝土热物理试验参数Table 4 Thermophysical parameters of silty clay and concrete

表5 粉质黏土力学性能试验数据Table 5 Mechanical property data of silty clay

图3 顶管结构Fig.3 Schematic diagram of jacking pipe

1.3 试验系统与数据采集

如图4 所示，自主研发系统的试验箱体尺寸为290 mm×330 mm×1 000 mm，内侧保温隔热，外侧加肋。顶管直径80 mm，壁厚1 mm，顶管水平间距30 mm，上覆土层厚200 mm。试验系统由土层、加载装置、冻结系统和数据采集系统组成。

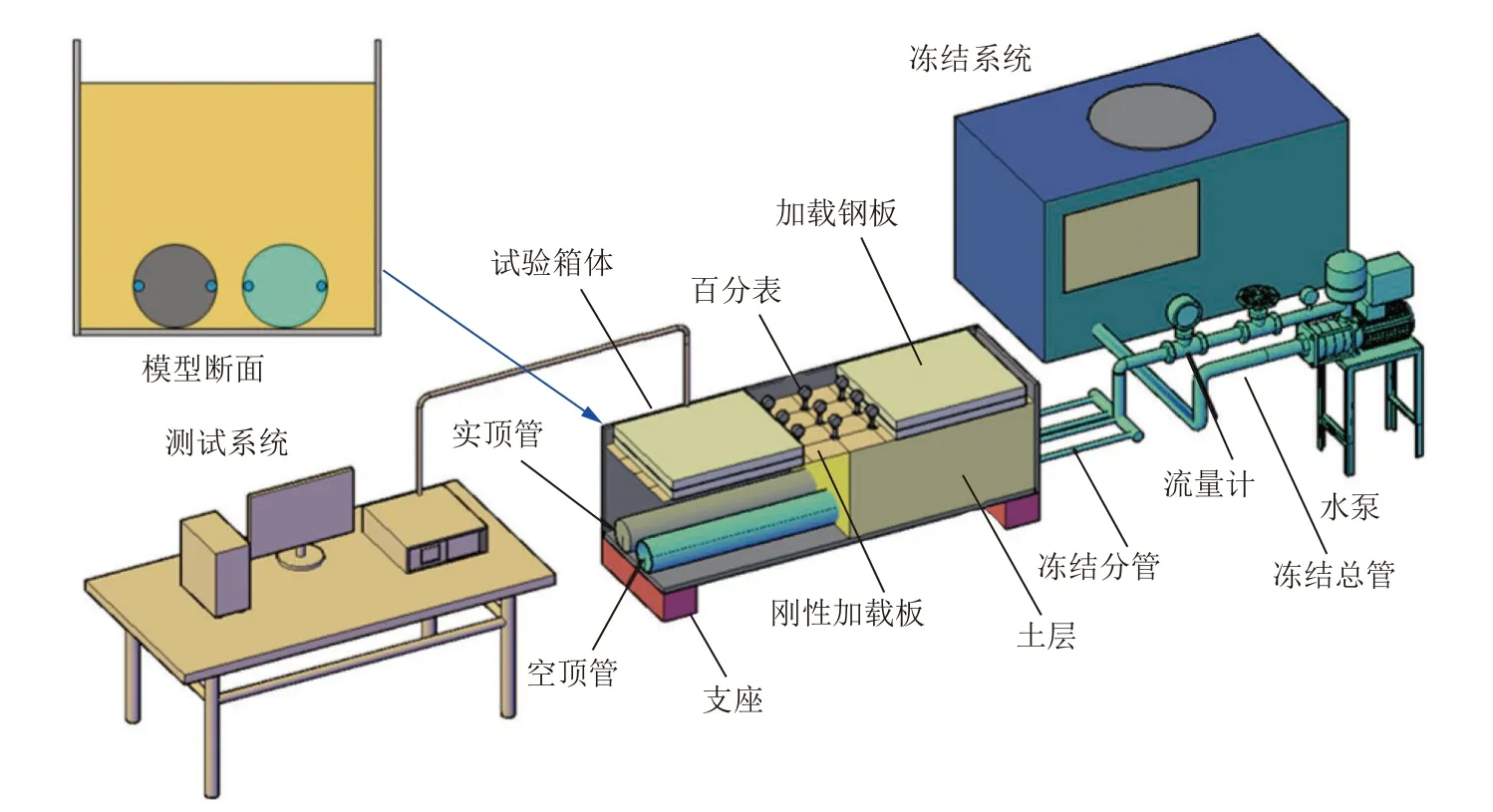
图4 试验系统三维图Fig.4 3D diagram of test system

(1) 土层模拟。采用粉质黏土(重塑)，约0.08 m3，按表4 含水率进行配制，采用分层填筑并压实。每层填完后用环刀取样测其含水率，以保证数据准确。

(2) 加载装置。由表2 相似比常数可知容重相似比为20，即模型土体的容重为原型土体的20 倍。考虑试验涉及冻结法，难以获取适合的替代材料，在试验中采用施加竖向静力荷载(配重钢板)的方法，经换算可得附加应力为0.076 MPa。

(3) 冻结系统。由制冷机组、水泵、流量计和冻结管路组成。顶管内冻结器通过分流器与冻结设备总管相连，冻结总管安装有流量计，控制冻结液流量约为0.1 m3/h。在冻结器表面布设温度测点，以精准控制冻结温度。

(4) 数据采集系统。包含温度、位移和应变测点以及TDS-602 多点数据采集仪(图5)。土体温度与冻胀位移测点均布置于复合结构梁的跨中截面，如图5a和图5b 所示；温度测点位于A—E轴线上，共计31 个；冻胀位移测点共9 个，分布于L 杆(实顶管中线)、C 杆(两顶管间中线)、R 杆(空顶管中线)，通过百分表读数来监测土层在冻结过程中的竖向位移变化。结构底部位移测点主要监测在荷载作用下复合结构底部挠度变化，分别在空、实顶管底部各布置位移计3 个，管间冻土底部1 个，如图5c 所示；应变测点布置如图5d 所示，以研究试验过程中钢顶管的变形规律。

图5 数据采集系统Fig.5 Data acquisition system

1.4 试验步骤

根据研究内容将试验过程分为“冻结”和“加载”两阶段，步骤如下：

(1) 开启制冷机组，设定冻结温度为-26℃；数据采集系统运行，设定为自动采集模式；打开制冷系统循环，冻结开始，降温计划如图6a 所示。

(2) 由时间相似比换算得冻结过程为480 min，之后减小制冷系统供冷量以维持稳定状态。

(3) 加载过程：如图6b 和图6c 所示，进行模型结构转换。在土层顶面进行分级加载，利用百分表记录结构底部竖向挠度，并继续监测温度、应变和位移数据。

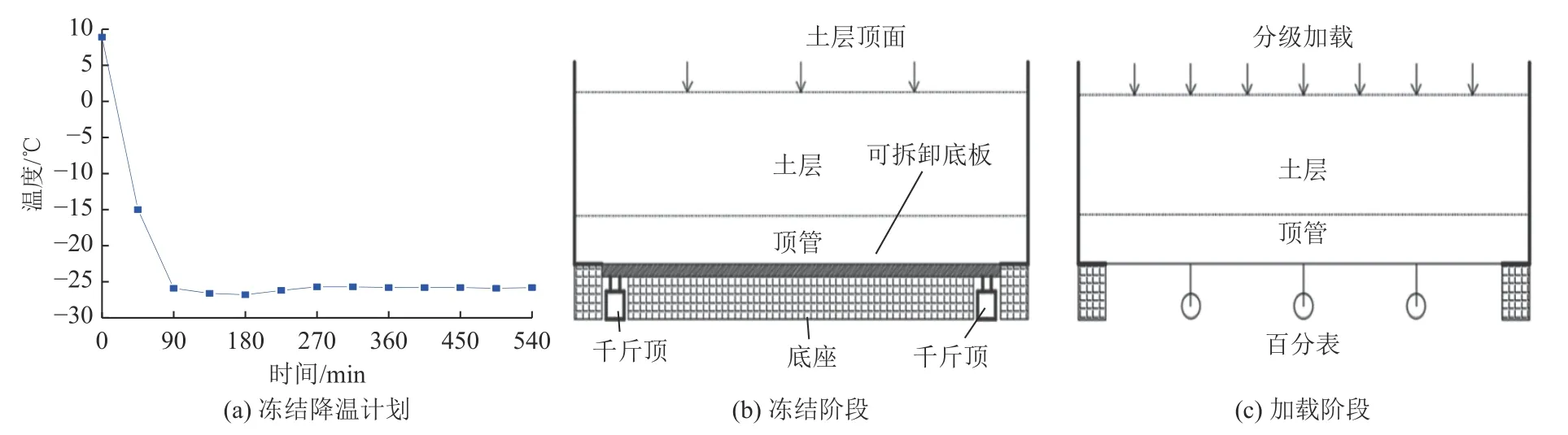
图6 降温计划与试验模型结构转换Fig.6 Cooling plan and structural transformation of test model

2 试验结果分析

2.1 冻结温度场分布规律

图7 为复合结构梁的跨中截面在480、540 min 时的冻结温度场分布。实顶管周围的整体温度低于空顶管，两顶管水平方向的冻土温度低于垂直方向，实顶管上方的冻土厚度大于空顶管上方。480 min 时，冻土厚度范围为105～163 mm，已冻区域面积占比51%；540 min 时，模型底部冻土由于结构转换而出现温度回升，与480 min 时相比，两顶管的水平侧与下侧的低温区域范围略有减小，而上方的冻土范围仍在缓慢扩展，此时冻土厚度范围为137～171 mm，已冻区域面积占比55%，管间冻土平均温度范围为-12.5～-20℃。可知冻土区域面积与温度分布均与空、实顶管的布置形式及其内部冻结器位置密切相关。

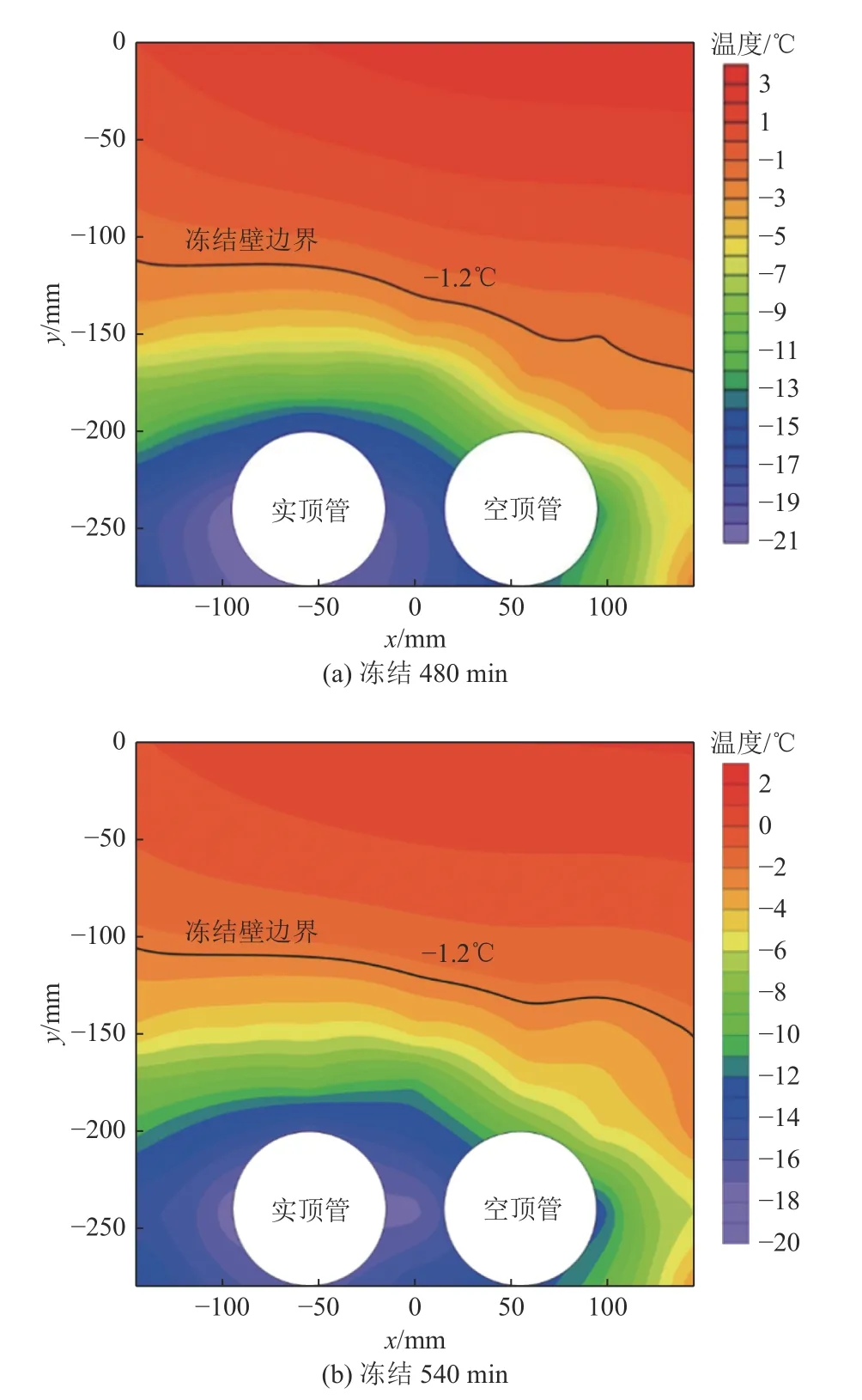
图7 不同冻结时间下的温度场等值线Fig.7 Contour map of temperature field under different freezing time

2.2 冻胀位移变化规律

由图8 可知，冻结过程中土体产生了较为明显的竖向冻胀变形。各点冻胀位移在0～40 min 变化较小，在60～160 min 急剧增大；L、C、R 三轴平均位移增长速率分别为0.005 6、0.005 2 和0.004 2 mm/min。180 min后，因冻结温度场的变化趋于稳定，冻胀位移曲线也随之进入缓慢增长阶段。同一测杆的测点位移值随深度增加而增大；实顶管上方冻胀变形最大，两顶管间次之，空顶管上方最小，整体规律与冻结温度场分布较为相似。横向对比发现，实顶管处和两顶管间更早地产生冻胀变形。480 min 时，不同土层深度的竖向平均冻胀位移分别为：0.74(1 号)、0.79(2 号)、0.88 mm(3 号)。

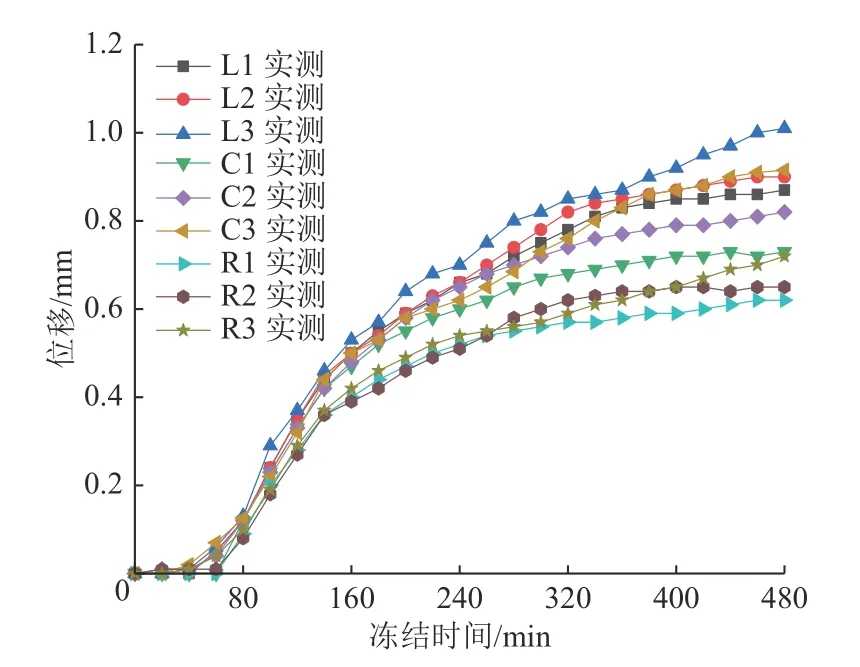
图8 土体竖向冻胀位移-时间曲线Fig.8 Vertical frost heave displacement-time curves

2.3 顶管变形规律

图9 为冻结阶段跨中截面处空、实顶管应变测点变化曲线。整体上看，空顶管各点应变值变化幅度明显大于实顶管，表明其在冻结过程中因受到土体冻胀力作用而产生相对较大变形；实顶管因其内部填充混凝土，整体刚度较大，仅在冻结前期应变值出现小幅变化，之后便逐渐趋于平稳。空顶管截面两侧应变测点(7 号和8 号)的应变值在冻结初期变化幅度最大，表明首先在两顶管间的水平方向快速形成冻土，使空顶管产生向右“弯曲”。随着冻土范围的扩大，至80 min时，实顶管已完全被冻土包裹；冻胀对空顶管水平方向变形的影响更加显著，其截面两侧应变峰值分别为-260 和261×10-6。在冻结阶段末期，两顶管外侧与上方的冻土范围仍在扩大，随着空顶管右侧的土体逐渐冻结，8 号应变值逐渐降低并最终转变为负值；480 min时，空顶管应变测点仅5 号为正值，表明截面左、右和下侧均为受压状态，仅上侧受拉。

图9 冻结阶段顶管跨中位置应变-时间曲线Fig.9 Strain-time curves at midspan of jacked pipe in freezing stage

由图10 可知，在加载阶段，实顶管截面上、下侧应变测点(17 号和18 号)的应变值随荷载增加呈线性增大趋势，峰值分别为-356 和362×10-6；左、右两侧应变测点(19 号和20 号)的应变值变化微小，表明其处于向下弯曲状态。空顶管截面上侧应变测点5 号的应变则呈现出较为明显的非线性变化特征，与6 号测点相比，两者的应变峰值分别为-729 和566×10-6，相差22%。经分析可得，因空顶管上方冻土厚度较小且温度较高，冻土强度较低，在荷载作用下可能会使空顶管截面的上侧部分区域被“压扁”，由此产生相对更大的形变。对比18 号和6 号测点数据可知，空顶管截面下侧的变形量为实顶管的1.6～1.7 倍。

图10 加载阶段顶管跨中位置应变-时间曲线Fig.10 Strain-time curves at midspan of jacked pipe in loading stage

2.4 “顶管-冻土”复合结构荷载-位移曲线

由图11 可以看出，实顶管底部各测点位移均随荷载增加呈线性增长趋势；跨中位移最大，峰值为3.04 mm，左右侧对称位置的位移值基本相等，平均峰值为2.29 mm。空顶管底部位移均随荷载增加呈非线性增长趋势，且前期增长速率略大，也表明其在弯曲变形过程中存在被“压扁”的可能；其跨中位移峰值为4.92 mm，左右侧位移平均峰值为3.64 mm。横向对比可知，相同位置处空顶管位移值约为实顶管的1.6 倍，表明复合结构中实顶管的承载力要优于空顶管。

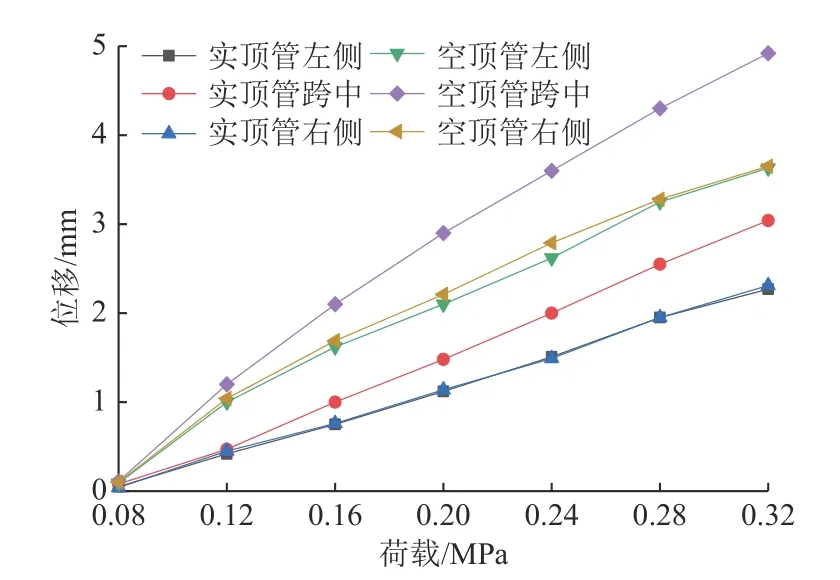
图11 顶管不同位置荷载-位移曲线Fig.11 Load-displacement curves at different positions of jacked pipe

图12 为跨中截面处两顶管和管间冻土底部荷载-位移曲线，同时引入“两管平均位移”曲线进行对比，即Vaver=(VHP+VCP)/2，其中，VHP为空顶管位移，VCP为实顶管位移，VFS为两顶管冻土位移，Vaver为两管平均位移。因空、实顶管间刚度差异，在荷载作用下空顶管底部位移应大于实顶管。且由各位移测点间几何关系可知，若视复合结构变形为线弹性，应满足等式VFS=Vaver。若不满足，则可判定管间冻土变形与两顶管已经不协调，可能会出现管间冻土与顶管脱离或开裂，进而导致封水功能失效。

由图12 可知，加载至0.24 MPa 后，管间冻土位移曲线与两顶管平均位移曲线开始分离，并逐渐偏向实顶管位移曲线；至0.32 MPa 时，管间冻土位移为3.73 mm，两顶管平均位移为3.98 mm，复合结构的封水功能可能已经失效，下文将通过数值模拟对上述分析加以验证。

图12 复合结构跨中截面处顶管与冻土荷载-位移曲线Fig.12 Load-displacement curves of jacked pipe and frozen soil at the midspan of composite structure

3 数值模拟验证

采用COMSOL Multiphysics 建立与试验模型尺寸一致的包含“管-土”接触与冻结冻胀耦合的三维模型，如图13a 所示。假定模型材料均为理想的弹塑性材料，沿复合结构长度方向(z轴)符合连续性与均匀性假设；顶管和土体在初始状态下完全接触，冻土服从Drucker-Prager 屈服准则[36-37]，材料计算参数按室内实验结果取值；模拟过程仅考虑温度场与力场的耦合，忽略土体冻结过程中水分迁移影响。

模型网格划分如图13b、图13c 所示。为实现有限元计算的简化，分别采用四边形和三角形网格对模型断面上的顶管与其余部分进行划分，然后通过“扫掠”功能沿z轴方向生成三维的六面体和棱柱单元。同时在接触面区域对网格进行细化以保证计算的精度与收敛性，模型平均单元质量为0.842 3，表明网格质量较好。

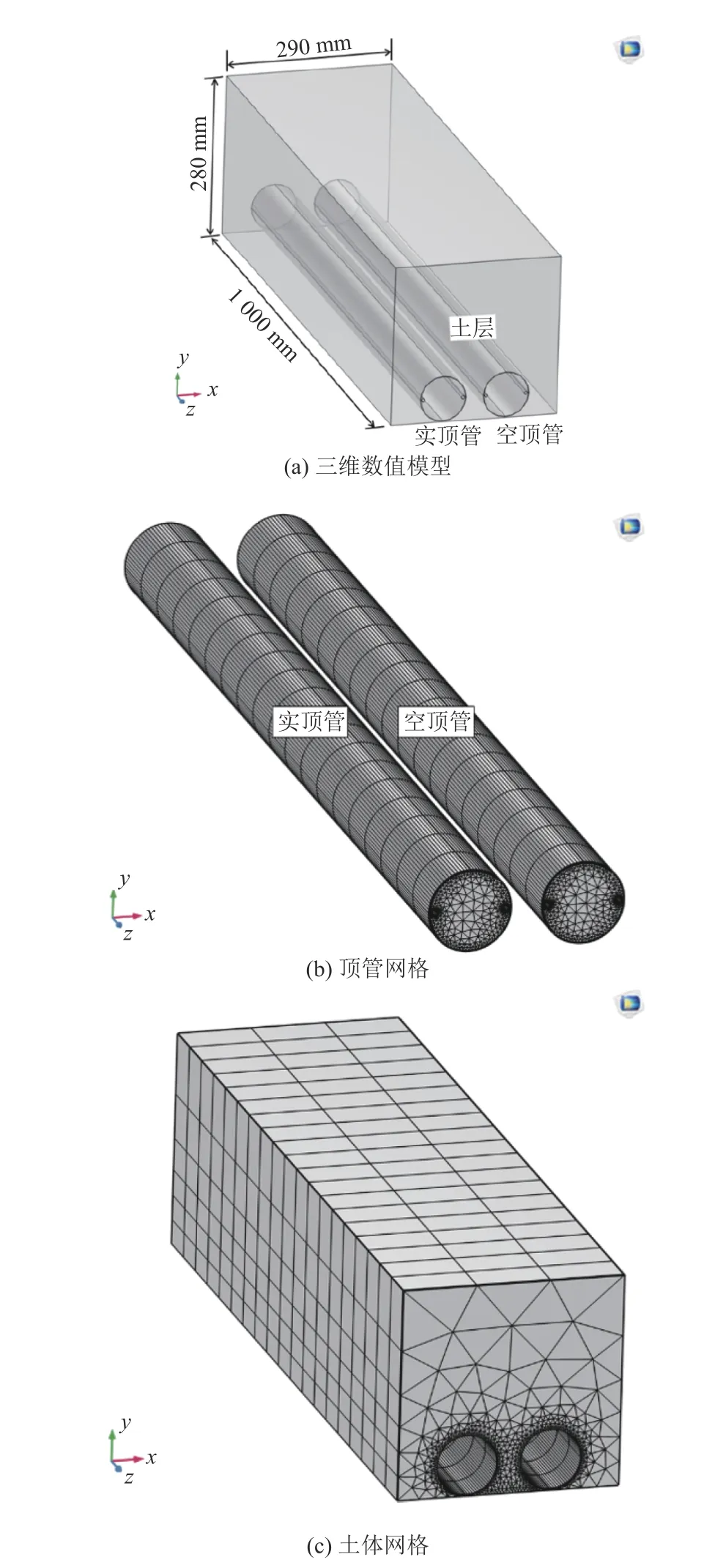
图13 三维模型与网格划分Fig.13 3D model and mesh generation

模型边界条件包括温度边界和力学边界：

(1) 温度边界包括冻结器外壁和复合结构外表面。冻结器外壁温度按试验对应温度测点的数据取值；在冻结阶段，复合结构4 个侧面和底面采用了保温措施，设为绝热边界，顶面因加载需要未设置保温，根据试验环境温度设为对流传热边界；在加载阶段，模型顶面和底面均设为对流传热边界。

(2) 根据试验内容，将模型顶面设为自由边界并施加相应的均布荷载；4 个侧面设置辊轴支撑，施加支撑面法向约束。在冻结阶段将模型底面设为固定约束；根据图7c 所示，在加载阶段将底面两端设为固定边界，中部设为自由边界。

3.1 计算结果对比

选取测温点D4 和位移测点C1 进行试验数据与模拟结果对比，如图14 所示。D4 测点温度模拟值在冻结后期略低于实测值，最大误差小于0.6℃；C1 测点竖向位移模拟值在后期略大于实测值，最大误差小于0.03 mm。其主要原因为建模过程中进行了相应简化，与绝对值相比上述误差可以忽略，数值模拟结果较为可靠。

图14 数值模拟与实测对比Fig.14 Comparison between numerical simulation results and test results

3.2 加载阶段顶管受力与变形分析

由图15 可知，空、实管上侧的接触压力均随荷载的增加而增大，实顶管的受力大于空顶管，同时因冻结温度场不均匀分布导致两顶管接触压力峰值均位于其上侧偏左的区域。加载至0.32 MPa 时，空、实顶管接触压力峰值分别为652、915 kPa。

图15 加载过程中不同荷载条件下顶管接触压力云图Fig.15 Cloud diagram of contact pressure of jacked pipe under different loading conditions

如图16 所示，空、实顶管的竖向位移也随荷载的增加而增大。因实顶管内部填充混凝土，刚度更大且不会被“压扁”，其竖向位移云图始终呈线性分布；而空顶管因刚度较小，其竖向位移云图呈现出较为显著的非线性分布特征。加载至0.08 MPa 时，其最大变形处位于跨中截面左上侧，为-0.74 mm，截面底部变形量为-0.7 mm；而此时实顶管跨中处最大变形为-0.41 mm。随着荷载的持续增大，空顶管最大变形区域逐渐由跨中截面左上侧开始向右侧扩展，表明其截面上部区域逐渐被“压扁”且范围也在逐渐扩大。加载至0.32 MPa 时，空顶管截面上侧最大变形量为-6.9 mm，截面底部变形量为-5.6 mm，二者相差1.3 mm；实顶管跨中截面竖向位移最大值为-3.5 mm。

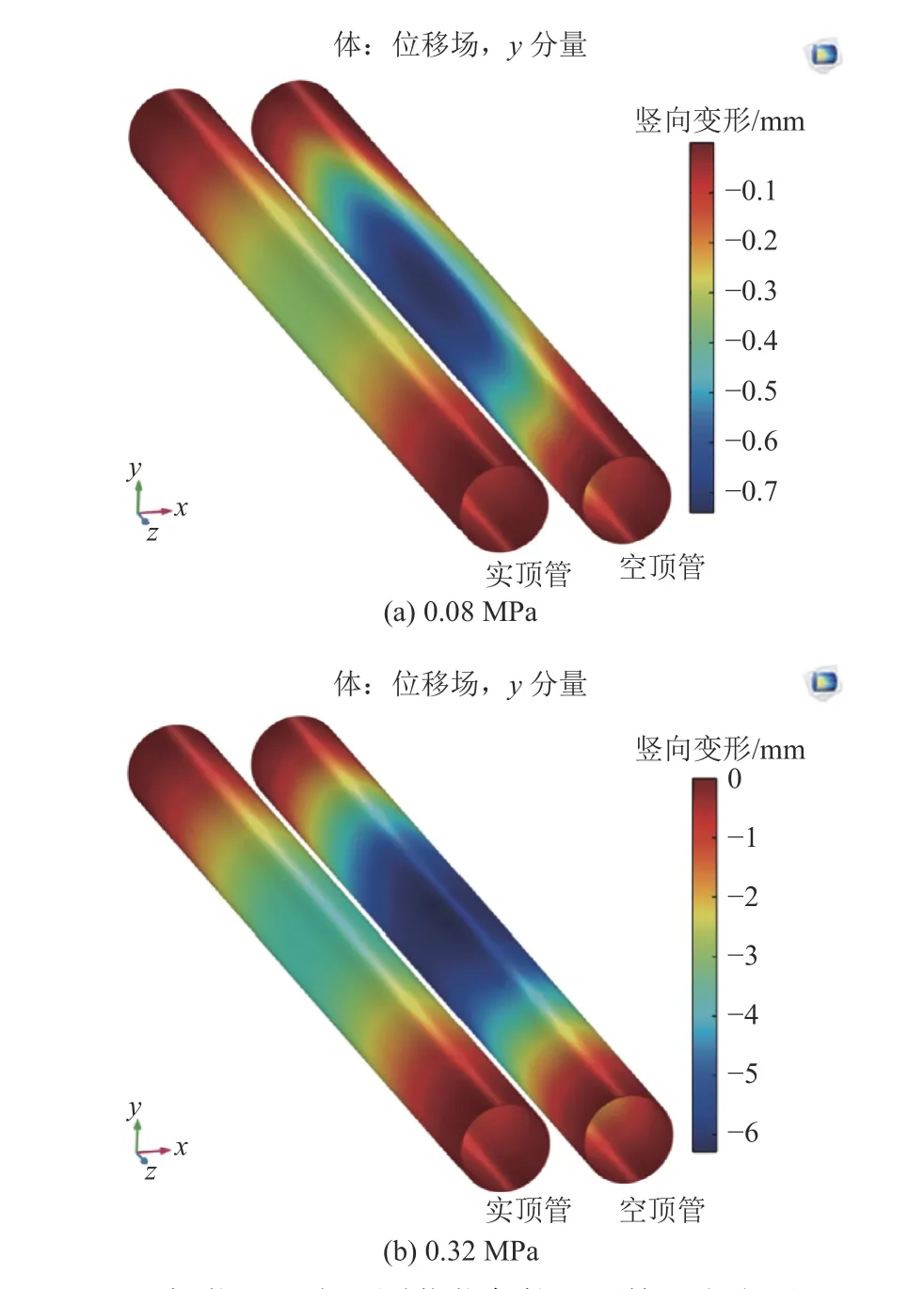
图16 加载过程中不同荷载条件下顶管竖向变形云图Fig.16 Cloud diagram of vertical deformation of jacked pipe under different loading conditions

结合试验数据和顶管受力分析结果可知，在加载的整个过程中，空、实顶管作为主要承载结构，其受力和变形特征存在显著差异。实顶管相对刚度更大且不会被“压扁”，其变形量较小且为线性变化，在复合结构中的承载力更高，在加载范围内也未出现屈服。空顶管跨中截面底部的位移变化包含了顶管的“弯曲”和“压扁”，因此呈现非线性变化特征，这种相对更大的变形也使其承载力要小于实顶管。

3.3 管间冻土受力分析

由图17 可知，复合结构的跨中截面处冻土Von Mises 应力也因其厚度和温度场的不均匀分布而呈现不对称性。应力峰值区域主要分布于两管之间和空顶管右侧，且大小随荷载增加而增大。加载至0.28 MPa时，管间冻土应力峰值为1.01 MPa，已超过其抗折强度平均值0.99 MPa。结合图12 分析可知，管间冻土位移曲线此时已与两顶管平均位移曲线分离，并逐渐偏向实顶管位移曲线，因此，可认为管间冻土已被破坏并产生开裂，管间封水已经失效。

图17 加载阶段复合结构跨中截面冻土Von Mises 应力云图Fig.17 Von Mises stress nephogram of frozen soil in midspan section of composite structure in loading stage

结合顶管分析结果可知，加载阶段两顶管产生竖向弯曲变形的同时因空顶管刚度较小，其上侧部分区域被“压扁”；随着荷载进一步增加，管间冻土发生破坏，进而导致结构封水失效。实际工程资料显示，拱北隧道“顶管-冻土帷幕”支护体系所受最大水土压力约为0.2 MPa，且断面开挖采取分台阶分部与“随挖随支护”施工，支护至开挖面间隔仅为0.4～0.8 m，参考本试验相似比常数可知，复合结构在此工况下满足承载力要求。

4 结论

a.“顶管-冻土”复合结构的冻结温度场因空、实顶管及其内部冻结器的布置形式呈现不均匀分布特征。土体竖向冻胀位移变化与冻结温度场的发展速率和分布规律相关，且冻胀量随深度增加而增大。

b.加载阶段顶管受力与变形均以竖向为主。因空、实顶管间刚度差异和冻土厚度不均匀的共同影响，空顶管竖向变形包含了“弯曲”与“压扁”并呈现非线性特征。

c.管间冻土首先与两顶管产生协同变形。加载至0.28 MPa 时，管间冻土Von Mises 应力峰值超过其抗折强度而发生破坏，进而导致管间封水失效。对比工程原型工况可知，复合结构满足承载力要求，实际施工过程中应对空顶管的变形规律、顶管间冻土帷幕的温度变化及其完整性进行重点监测。

d.本文依托自主研发构建的相似模型试验系统和COMSOL Multiphysics 计算平台，对“一空一实”两根顶管组合下的“顶管-冻土”复合结构力学特性进行了试验研究与模拟验证，对管幕冻结法的施工监测给出指导建议，也为热力耦合数值计算模型提供了验证依据。后续可基于本试验系统平台，考虑不同冻结时间、不同顶管数量和组合方式、不同土质和土性等因素展开进一步研究，以期为该工法的推广应用提供参考。