Construction of the rat brain spatial cell firing model on a quadruped robot

Naigong Yu|Yishen Liao|Hejie Yu|Ouattara Sie,4

1Faculty of Information Technology,Beijing University of Technology,Beijing,China

2Beijing Key Laboratory of Computational Intelligence and Intelligent System,Beijing,China

3Engineering Research Center of Digital Community,Ministry of Education,Beijing,China

4College of Robotic,UniversitéFélix Houphouët‐Boigny,Abidjan,Côte d'Ivoire

Abstract Physiological studies have shown that rats in a dark environment rely on the limbs and vestibule for their self‐motion information,which can maintain the specific firing patterns of grid cells and hippocampal CA3 place cells.In the development stage of rats,grid cells are considered to come from place cells,and place cells can be encoded by hippocampal theta cells.Based on these,the quadruped robot is used as a platform in this paper.Firstly,the sensing information of the robot's limbs and inertial measurement unit is obtained to solve its position in the environment.Then the position information is encoded by theta cells and mapped to place cells through a neural network.After obtaining the place cells with single‐peak firing fields,Hebb learning is used to adjust the connection weight of the neural network between place cells and grid cells.In order to verify the model,3‐D simulation experiments are designed in this paper.The experiment results show that with the robot exploring in space,the spatial cells firing effects obtained by the model are consistent with the physiological research facts,which lay the foundation for the bionic environmental cognition model.

1|INTRODUCTION

Bionics promotes the adaptability of robots to unstructured environments.At present,bionic robots have been widely used in aerospace,underwater exploration,disaster rescue,and other occasions[1].In the future,bionic robots will work for humans in unknown environments that humans cannot reach[2].Environmental cognition is a unique ability of mammals.For bionic robots,having the same intelligence as mammals is necessary to realize navigation tasks quickly and accurately[3].How to give this ability to robots is a common concern in the fields of artificial intelligence,robotics,and neuroscience[4].As a member of the mammalian family,rats also have excellent navigation abilities.Physiological studies have shown that the entorhinal–hippocampal formation is a key brain region that enables environmental cognition and navigation in rats[5],and a variety of neurons(spatial cells)with specific firing functions in the part of the entorhinal–hippocampal structure are the basis[6,7].In 1971,O'Keefe found a kind of neuron with a specific firing effect in the rat hippocampus[8].When the rat is in a particular position in space,the neurons have firing activity.These neurons are called place cells,and the corresponding firing area is called the place field[9].In 2005,Hafting found another neuron with a strong firing effect on the spatial position in the entorhinal cortex of the rat brain[10].Different from place cells,when rats explore in the spatial region,the firing activities of these neurons form a regular hexagonal grid,which evenly covers the whole spatial area.These neurons are called grid cells,and the firing area in their corresponding space is called the grid field[11].

Place cells and grid cells provide the representation of spatial location[12],so how are these spatial representations formed?Physiologists found that the input signals of place cells and grid cells came from the spatial information provided by the external environment and self‐motion signals[13,14].For place cells,physiologists have confirmed through several experiments that hippocampal place cells of different subgroups are controlled by different cues,and some place cells are controlled by only one cue[15].In the hippocampal CA3 region,manipulation of external visual cues without changing the environment's location significantly changed the firing frequency of the place cells.Still,they did not change the location of the firing field[16].Subsequent studies also confirmed that place cells in the hippocampal CA3 region encode self‐motion information,while place cells in the CA1 region encode both the external environment and self‐motion information[17].

As a position representation based on self‐motion,grid cells'specific firing mode is maintained mainly by the input of self‐motion signals[18],which is similar to CA3 place cells.So is there excitatory transmission between place cells and grid cells?In the past,the mainstream view was that grid cells are the upstream neurons of place cells,and a variety of models based on this view have been proposed,such as the competitive neural network[19–20],independent component analysis model[21],and radial basis function neural network[22].However,this view ignores the differences of rats at different ages.Wills'study in 2010 revealed how spatial neurons in the rat hippocampal structure develop with age,in which place cells mature gradually within 3–4 weeks after eye‐opening,while grid cells develop later but rapidly reach maturity[23].In 2013,Bonnevie found through physiological experiments that when the information transmission pathway from grid cells to place cells in young rats was cut off,the firing field of place cells remained stable.But when hippocampal place cells were inactivated,the grid field pattern almost disappeared[24].Therefore,it can be speculated that grid cells act as the input of place cells when rats are in adulthood.But when the rats are young,the place cells may be used as the input of grid cells.

The specific firing patterns of CA3 place cells and grid cells were maintained by the input of self‐motion information.So how do rats perceive and transmit self‐motion information?Physiological research shows that without visual input,rats mainly rely on the feedback information of vestibule,muscle,tendon,and joint to obtain self‐motion signals so as to achieve path integration[25].In the rat brain hippocampus,there is a kind of neuron that regularly fires at the frequency of 4–12 Hz,called theta cells[26].Theta cells take the self‐motion information as the input,which is thought to encode velocity‐controlled oscillator(VCO)signals predicted by oscillatory interference.VCO signals can synthesise arbitrary spatial tuning functions[27],so they can also generate the firing field of place cells.

Based on the above research status,we can infer the development process of spatial cells in the brain of young rats.That is,when rats explore the environment,self‐motion information is obtained through the vestibule and limbs,and then self‐motion information is used as the development signal of spatial cells.So how should we simulate such a process?It involves two fundamental problems:one is how to simulate the perception process of self‐motion information in rats,and the other is how to make grid cells spontaneously generate regular hexagonal firing fields under the input stimulation of place cells.

Therefore,this paper proposed a method for constructing the rat brain spatial cell firing model on a quadruped robot,which has made contributions mainly in the following aspects:

1.To be closer to the physiological structure of real rats,this paper is the first work that uses a quadruped robot as the carrier to realise the construction of the rat brain spatial cell firing model.The robot's position in the environment is calculated by obtaining the sensor information of the robot's limbs and inertial measurement unit(IMU),simulating the rat's motion state estimation when only the self‐motion information is input.

2.The specific phase relationship pattern between VCO signals is introduced to construct the place cell firing model in this paper,which can generate single‐peak place fields with the path integral information as input.

3.In order to simulate the change of grid cell firing characteristics,Hebb learning rules are used to adjust the neural network connection weights between place cells and grid cells.

The rest of this paper is organised as follows.Section 2 reviews the related work with limitations of previous research.Section 3 introduces the construction process of the whole model.The experimental results are demonstrated in Section 4 while discussion and conclusion are presented in Section 5 and Section 6.

2|RELATED WORKS

At present,the bionic computing model based on the cognitive mechanism of the rat brain mainly has two research directions:One is to simulate the information transfer and specific firing mechanism of various spatial cells.The research on place cells mainly constructs the firing model with grid cells as input,which has been described in Section 1.As for grid cells,their firing models mainly include the oscillatory interference model[28,29]and the continuous attractor network model[30–32].This kind of model takes the self‐motion information of rats as the input source,mainly showing the firing performance of mature grid cells,but it does not show the gradual change of the grid field during their development.In 2013,Grossberg proposed a grid cell firing model with stripe cells'firing rate as input,which self‐organised to form the grid field by adjusting synaptic weights.However,this model is still based on the theory of the attractor model,and it does not use place cells'firing rate as information input[33].In 2014,Castro proposed a grid field generation model,whose input information is only provided by place cells.But this model makes the grid field cover the whole spatial area by increasing the number of place cells,and it does not involve the process of dynamic adjustment of connection weights[34].In 2017,Urdapilleta et al.proposed a firing model with place cell inputs to generate discrete grid scales.Still,their ratios are not constant or constant‐on‐average unless explicitly tuned[35].In 2018,Weber et al.improved the continuous attractor network model by using the excitability and inhibitory plasticity mechanism.And they found that spatial cells can quickly self‐organise and stabilise from spatially modulated feedforward input[36].In 2021,DiTullio et al.reviewed that place cells play an essential role in generating,developing,and maintaining grid fields[37].

The other direction is localisation and map construction of mobile robots based on the neurobehavioral theory of the rat brain.The RatSLAM research group of the University of Queensland has made extensive studies on the cognitive computational model of the rat brain[38,39].They proposed a mature localisation and map construction method,the core part of which is called the pose cell.After that,researchers also put forward many improved models based on RatSLAM[3,40,41],but the pose cells are not in the rat hippocampus.Therefore,this model mainly imitates the neurobehavioral characteristics of rats rather than the anatomical structure and physiological characteristics of hippocampal structure[42].

3|CONSTRUCTION OF THE MODEL

3.1|Overall structure of the model

In this section,the rat brain spatial cells firing model of the quadruped robot is described in detail.The overall structure and operation mechanism of the model are shown in Figure 1.The running steps of the model are as follows:1.Firstly,the sensor information of the robot's limbs and IMU is obtained to calculate its position in the environment.2.Position information was encoded by theta cells and mapped to place cells through a neural network.3.After obtaining the place cells with single‐peak firing fields,Hebb learning is used to adjust the neural network connection weights between place cells and grid cells so that they can gradually form regular hexagonal grid fields throughout the whole space.

3.2|Position calculation of the quadruped robot

Rats are quadruped rodents.In order to get closer to the actual situation of rats'exploration process in the environment,this paper uses the quadruped robot as the carrier to calculate its position in the environment by obtaining the robot's limb joint angle,IMU information,and foot touchdown signal.

The overall schematic diagram,including each joint,foot‐end,coordinate system,and single‐leg joint angle of the quadruped robot,is shown in Figure 2 and Figure 3.

In Figure 2,A1,B1,C1,D1represent the hip joints of the quadruped robot,andA2,B2,C2,D2represent the foot‐end of each leg.The length of each thigh is set asl1,and the length of each calf is set asl2.The distance between the front and rear hip joint is set asL.The distance between the left and right hip joint is set as D.The red line represents the external coordinate system with the normal projection of the robot centroid on the ground at the initial time as the origin and the initial orientation as the positive direction of theX‐axis.The green line represents the body coordinate system with each hip joint as the origin.In Figure 3,θ1,θ2,andθ3represent each joint angle of a single leg.The forward kinematics solution can be used to calculate the position of the foot‐end in the hip joint coordinate system.Let the coordinate of theith leg's foot‐end in the hip coordinate system beRi=[xi,yi,zi];its mathematical expressions are as follows:

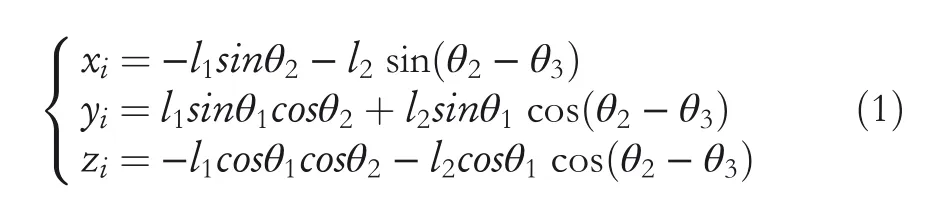
The coordinates of the robot's centroid in the external coordinate system are equal to the average of four hip joints'coordinates,so the coordinates ofA1,B1,C1,D1in the external coordinate system need to be solved.First,use the spatial geometric relationship of the quadruped robot's physical structure to give a solution equation.The mathematical expressions are as follows:

FIGURE 1 Schematic diagram of the overall operation mechanism of the model

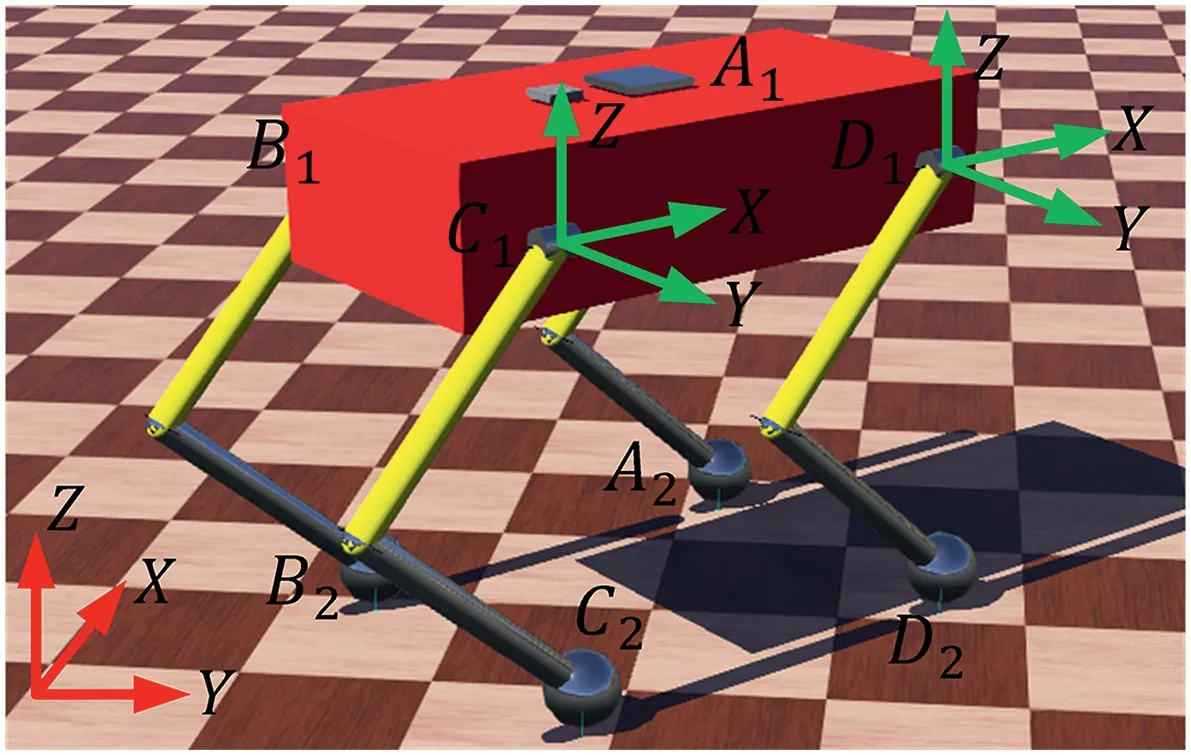
FIGURE 2 Overall schematic diagram of the quadruped robot

FIGURE 3 Schematic diagram of the quadruped joint angle

Then use the relationship between the IMU information and the coordinates of the four hip joints to give the solution equation.Let the normal vector of the planeA1B1C1D1beF→,and the unit vectors along the three axes of the body coordinate system are.Let the projection vector ofon the YOZ and XOZ plane beand.The mathematical expressions of the equation are as follows:

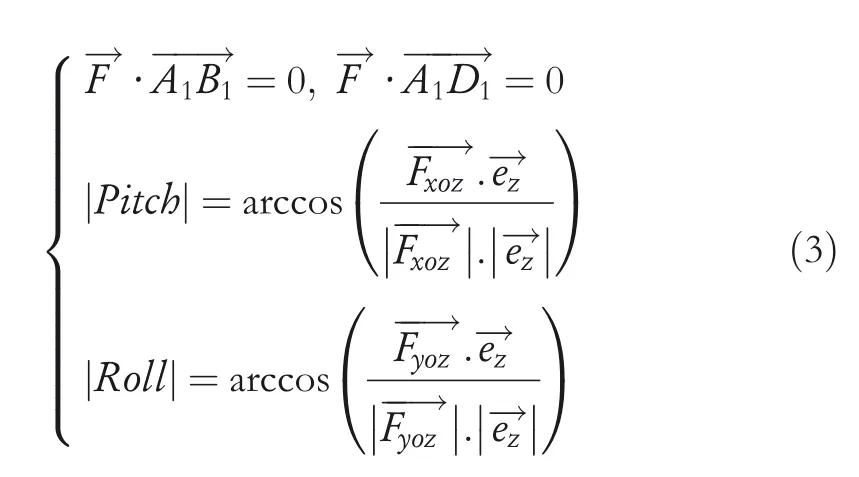
In this paper,the motion of the quadruped robot adopts the Trot method for gait planning.The characteristic of the Trot gait is that the two diagonal legs move in pairs[43].When the foot ends of legs A and C touch the ground,the coordinates of the foot ends of legs A and C in the external coordinate system are taken as known quantities,and the coordinates of each hip joint in the external coordinate system are solved using the above geometric relationship.Then obtain the coordinates of the robot's centroid in the external coordinate system(the position in the physical environment).And if the feet of legs B andDtouch the ground,the solution will be solved in the same way.The path integration of the quadruped robot can be realised by using the above method.

3.3|Place cells firing model

Physiological studies have shown that there are many VCOs in the rat brain.Each VCO signal is produced by the theta cell.However,such a population of theta cells can encode a basis set that synthesises arbitrary spatial tuning functions.The calculation process of the place cell firing model based on the VCO signal[27]is as follows.

Firstly,the instantaneous phase expression of the VCO signal is given as follows:

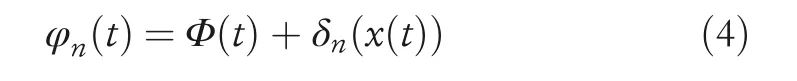
In Equation(4),x(t)represents the robot's position in the external coordinate system.Φ(t)represents the‘reference phase’common to all VCO oscillators,and its mathematical expression is as follows:

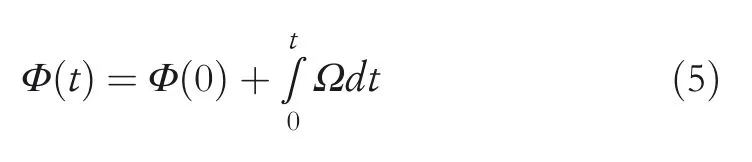
In Equation(5),Φ(0)andΩrepresent the initial phase and base frequency.δnrepresents the reference phase offset of thenth VCO oscillator,which depends on the position of the robot.Its mathematical expression is as follows:

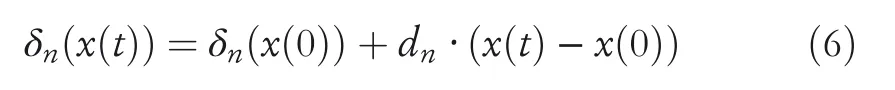
In Equation(6),dnandδn(x(0))represent the preference vector and the initial reference phase offset of thenth VCO oscillator.It can be seen from Equation(6)that when the robot is atx(t),the reference phase offset of thenth VCO oscillator at this position will be strictly determined by the distance between the robot's current position and the initial position‖x(t)−x(0)‖and the preference vectordn.In addition,since all VCO oscillators have the same reference phase,the phase shift between them will also be strictly dependent on the robot's position.Thus,each position in the space will be encoded by a specific phase relation pattern between VCOs,which means that interference between VCO signals generated by any unique subset of theta cells will form a different spatial envelope curve.Suppose the output of VCO oscillators is superimposed asI(t),and its mathematical expression is as follows:

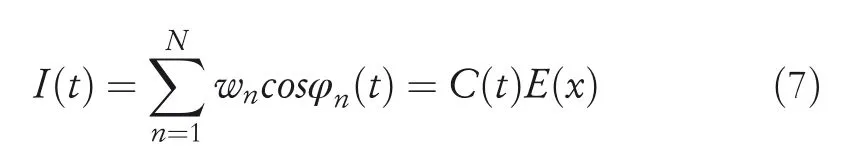
In Equation(7),wnrepresents the connection weight between theta cells and place cells.It can be seen from Equation(7)that the output sum of VCO signals can be rewritten as the product of two terms:carrier signalC(t)that changes with time and envelope signalE(x)that changes with space.The mathematical expression ofC(t)is as follows:

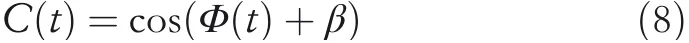
In Equation(8),βrepresents the initial phase of the carrier signal,and its mathematical expression is as follows:

Let the coordinate of the place field centre in the external reference system bep,the envelope signalE(x)can be expressed as the modulus of the sum of complex exponentials,and its mathematical expression is as follows:

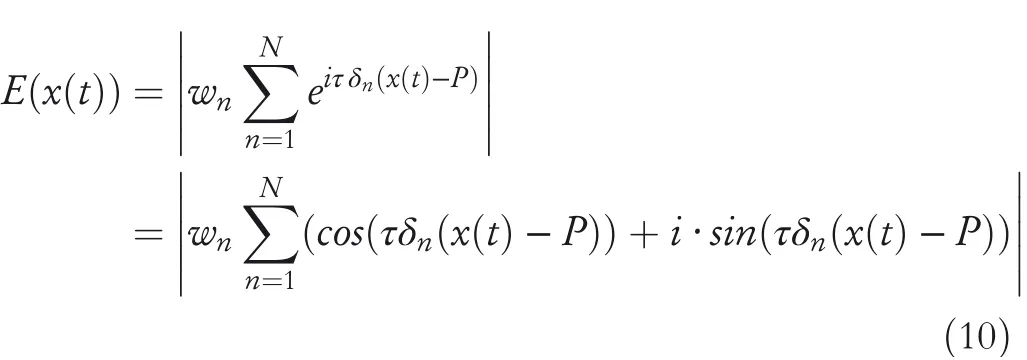
In Equation(10),τ=γ·2k−1.γis the minimum amplitude of the place cell.kis the place field adjustment factor,and its value is a number greater than or equal to one.Therefore,the mathematical expression of the place cell firing rate can be written as shown in Equation(11),whereH(x)stands for the Heaviside function andεstands for the firing threshold.

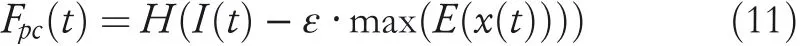
3.4|Grid cells firing model

Physiological studies have shown that synapses connect the place cells and grid cells.Different shapes of synapses have different functions,in which asymmetric synapses conduct excitatory firing and symmetric synapses conduct inhibitory firing.A grid cell that connects with multiple place cells receives both excitatory and inhibitory signals.The mechanism of information transfer from place cells to grid cells is shown in Figure 4.

Firstly,the set of place cells and grid cells are as follows:

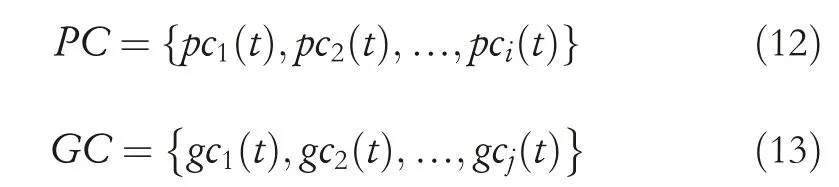
Let the firing rate of thejth grid cell be defined asgcj(t),the mathematical expression is as follows:

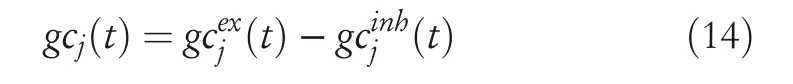
In Equation(14),gcjex(t)andgcjinh(t)represent the excitatory input and inhibitory input received by grid cells.The mathematical expressions ofgcjex(t)andgcjinh(t)are as follows:

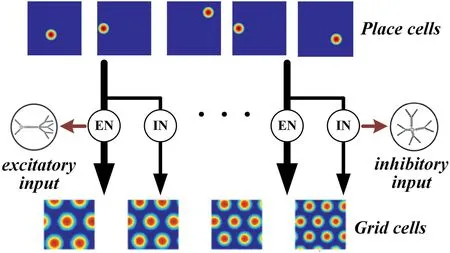
FIGURE 4 Schematic diagram of information transfer from place cells to grid cells

In Equations(15)and(16),Npcrepresents the number of place cells.Wij(t)represents the connection weight of the neural network.ηexandηinhrepresent the signal gain of the excitatory input and inhibitory input.pciex(t)andpciinh(t)represent the excitatory and inhibitory output from place cells.After obtaining the firing rate of place cells and grid cells,the connection weights can be adjusted.Physiological studies have shown that when the rats arrive at a new unknown environment,the grid field covering the spatial area will be gradually established as the rats explore the environment.But if the rats stop exploring the environment or leave the current environment,the grid field covering the space area needs to be re‐established when they start exploring the environment or return to the environment.It means that when rats leave the current environment,their memory of the environment will gradually weaken.In order to simulate the process,Hebb learning with a forgetting mechanism is used to adjust the connection weights.Hebb learning is an unsupervised learning method that can spontaneously adjust the connection weight according to the neuron firing rate before and after synapses.The mathematical expressions are as follows:

In Equation(17),ϑrepresents the learning rate of neural network,ΔWijrepresents the change of connection weight.In Equation(18),ρrepresents the forgetting factor of the neural network.It is obvious that whenΔWij=0,Wij(t+1)=(1−ρ)Wij(t),iftapproaches infinity,Wijis also infinitely close to zero.It means that the contact efficiency between presynaptic neurons and postsynaptic neurons will decline over time without learning,which is called forgetting.

During the development process of grid cells,the method of gridness score calculation is used to represent the maturity of grid cells[44].Firstly,the autocorrelation of the firing is drawn by Pearson differential correlation,and the peak centre of the autocorrelation map is extracted.Then rotate the autocorrelation graph with the peak as the centre 60° and 120°(on‐peak),and rotate 30°,90°,150°(off‐peak)at the same time,the shift correlationEjrotθ(t)between autocorrelation graph and self‐correlation graph after rotation is calculated as

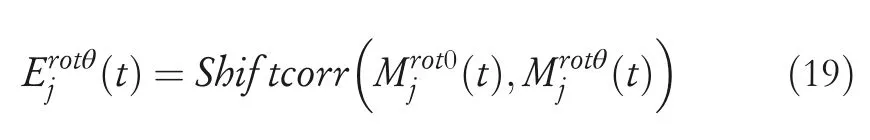
Finally,the minimum difference of the correlation value after on‐peak rotation and off‐peak rotationSj(t)is calculated as the gridness score,and its mathematical expression is shown in Equation(20).The larger the gridness score is,the closer its shape is to the standard hexagonal firing field,which means the grid cell is more mature.

4|EXPERIMENTS AND RESULTS

4.1|Experimental description

This paper uses the Webots software to design 3‐D simulation experiments.In the simulation,rigid body,angle sensor,motor,angle sensor,and IMU are used to build the physical model of the quadruped robot as shown in Figure 5.

The robot's body is set to a rectangular parallelepiped of 0.35×0.25×0.7 m,and the IMU is installed on the top of the body platform.The body and thigh,and thigh and calf are connected through joints,and each joint is equipped with a driving motor and an angle sensor.Touch sensors are installed on all foot‐ends to detect the landing condition of the quadruped robot.The length of each thigh is set as 0.35 m.The length of each calf is set as 0.35 m.The distance between the front and rear hip joints is set as 0.6 m,and the distance between the left and right hip joints is set as 0.45 m.The friction coefficient of the foot‐end is increased to ensure that there is no slippage between the foot‐end and the ground.However,there will still be cumulative errors in the long‐term movement.Therefore,when the robot moves to the regional boundary,the Global Position System signal is used to correct the position of the robot.

FIGURE 5 Physical structure diagram of quadruped robot built in the Webots software

4.2|Place cells firing experiment

The size of the simulation environment is set to 10×10 m,and the robot explores autonomously in this environment.The schematic diagram of the quadruped robot exploring the environment is shown in Figure 6.

Then the position information was input to theta cells.Subsequently,theta cells generate VCO signals to synthesise the spatial tuning function of place cells.Each place cell is connected with 12 theta cells,and the connection weights between each place cell and the theta cells connected to it are the same.The minimum firing rate amplitude of the place cellγis set to 0.3.The firing thresholdεis set to 0.7.The preference vector direction of the VCO signal generated by theith theta cell is set to 2π(i−1)/12,and the frequency of all VCO signals is set to 0.125 rad/s.Figure 7 shows the firing effect of the place cell with the robot exploring the environment.It can be seen from the figure that as the exploration trajectory of the robot gradually fills the whole area,single‐peak firing fields of the place cells become clear,which verifies the effectiveness of the model.

As for the place cells,the firing location depends on the place field centres'coordinates in the external reference system.And the firing field radius is related to the connection weight between place cells and theta cells.Then,the firing experiments of different place field centres and radii are carried out.Figure 8 shows the firing effect of different place field centres'coordinates when the firing field adjustment factorkis set to 3.0.Figure 9 shows the firing effect of different place field radii when the firing field adjustment factorkof each place cells group are set to 1.0,1.5,2.0,2.5,3.0 and 3.5.

4.3|Grid cells firing experiment

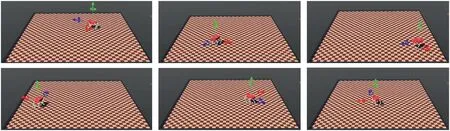
FIGURE 6 Schematic diagram of quadruped robot exploring the environment

FIGURE 7 Place cells firing effect with the robot exploring the environment

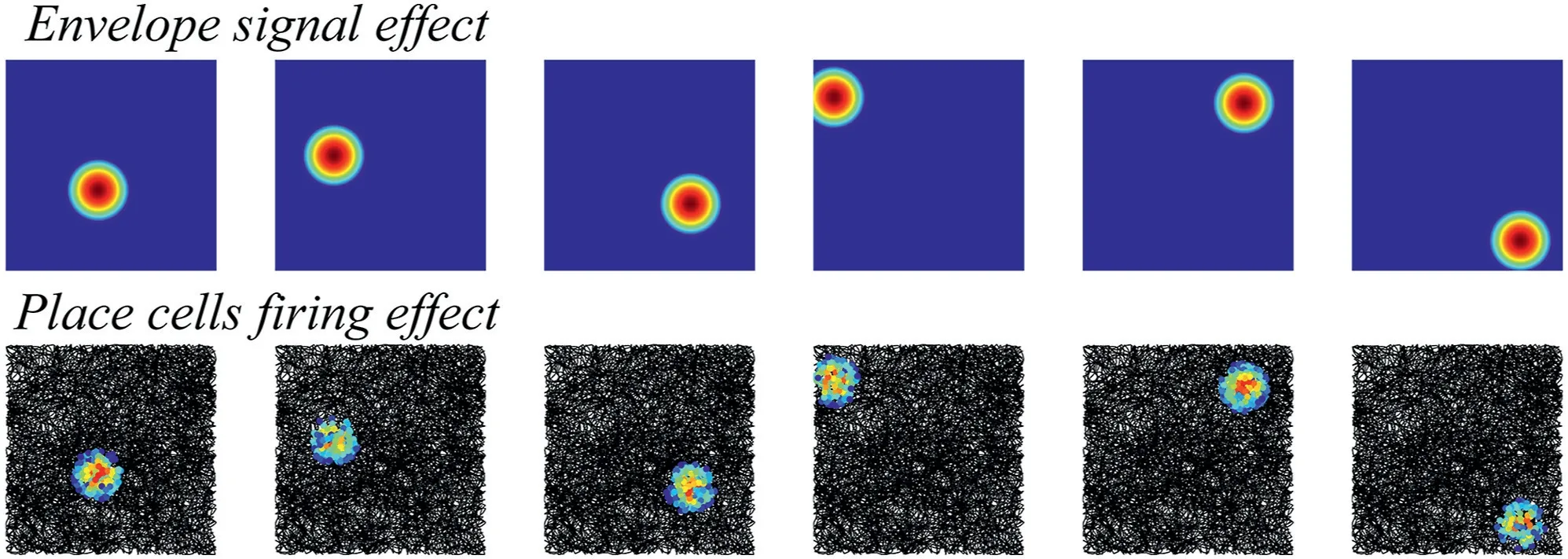
FIGURE 8 Firing effect of different place field centres'coordinates

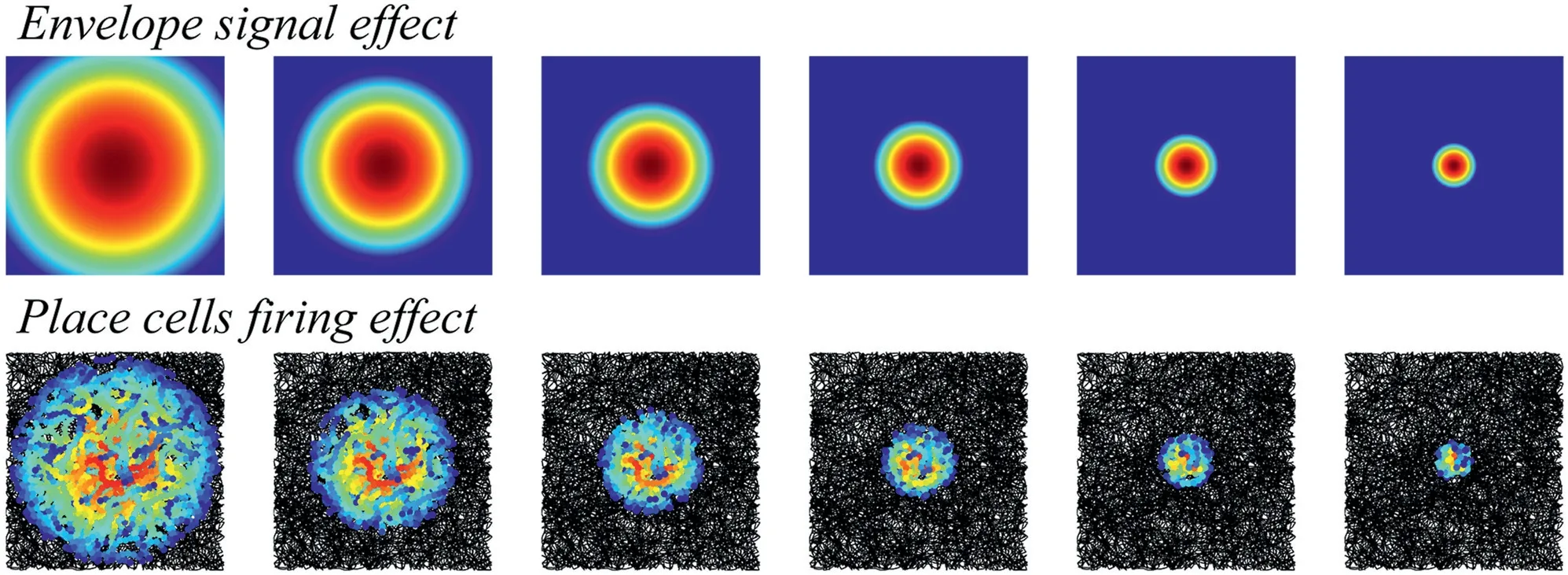
FIGURE 9 Firing effect of different place field radii

After obtaining the place cells with single‐peak firing fields,the firing experiment of grid cells was carried out.The number of grid cells to be developed is set to 1,the number of place cells is set to 1500,and the coordinates of all place field centres are randomly selected in space.The firing field adjustment factorkis set to 3,and the learning rate of the neural networkϑis set to 0.005.The signal gain of excitatory input and inhibitory inputηexandηinhare set to 1 and 0.5.The initial connection weights of the neural network are randomly selected from 0 to 1.The change of the grid field with the robot's exploration in the environment is shown in Figure 10.It can be seen from the figure that when the robot starts to explore the environment,the shape of the grid field is irregular.As time goes on,the movement trajectory of the quadruped robot gradually changes from sparse to dense,covering every part of the space area.In this process,the grid field gradually forms a regular hexagon,covering the whole space area,which verifies the effectiveness of the model.

As the information input source of grid cells,the different properties of place cells will also lead to the different development results of grid cells.For place cells,the radius of the firing field is an important parameter,and the variable which determines the radius of the place field is the firing field adjustment factor.In order to explore the effect of the place field adjustment factor on the development of grid cells,four groups of experiments were carried out.The firing field adjustment factor of each place cells group are set as 3.0,3.5,4.0,and 4.5,and the number of grid cells in each group is set as 100.Other parameters are consistent with the above.The change of the grid field and the gridness score in each group are shown in Figure 11 and Figure 12.

As it can be seen from Figures 11 and 12,the smaller the adjustment factor,the faster the grid cell develops and the more regular the shape of the grid field.Grid field distance is an important attribute of the grid field,which represents the distance between adjacent grid nodes.Physiological studies showed that the grid field distance in the entorhinal cortex from dorsal to ventral showed an increasing change,which is consistent with the increasing change of the response domain of place cells from dorsal to ventral of the hippocampus.

In addition,as it can be seen from Figure 11,the different values of the place field adjustment factor directly determine the grid field distance after the grid cells mature in this model.The smaller the place field adjustment factor is,the larger the grid field distance is.This is consistent with the physiological discovery of multi‐scale grid cells in the entorhinal cortex of the rat brain,which verifies the effectiveness of the model.

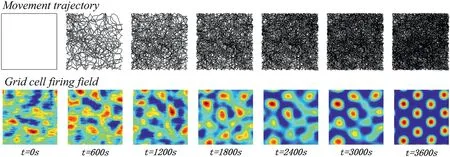
FIGURE 1 0 Change of the grid field in the process of the robot exploration environment

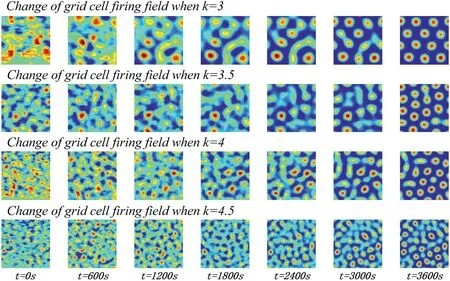
FIGURE 1 1 Effect of the grid field change at different place field radii

Physiological studies show that when rats stop exploring the environment,their memory will gradually weaken,so the grid field covering the spatial area will gradually disappear.In order to verify whether the model can simulate the process,the following experiment was designed.The number of grid cells is set to 100.The number of place cells is set to 1500.The firing field adjustment factorkof all place cells is set to 3.The forgetting factorρis set to 0.0002.

The duration of the experiment is set at 120 min and divided into two stages.The first 60 min of the experiment is the learning stage,and the experimental parameters and methods are consistent with those described above.The second 60 min of the experiment is the forgetting stage,in which the robot stops exploring the environment.Experimental results are shown in Figure 13 and Figure 14.It can be seen from the figure that with the robot exploring the environment,the grid field gradually changed from a chaotic firing field to a regular hexagonal firing field in the first 60 min.However,since the robot stopped exploring the environment,the grid field gradually changed from a regular hexagon to a chaotic firing field,which was consistent with the physiological research facts,and verified the effectiveness of the model.

4.4|Experiment of comparison

In order to verify the robustness of our model,it is compared with the oscillatory interference model and the continuous attractor network model[37].The specific experimental method is as follows:the robot starts from uniform motion,gradually increases the speed change range,and then records the grid cell firing effects of the three models under different speed change ranges.Other experimental methods are consistent with the previous text.

To ensure the contrast of the experiment,the grid field parameters of the three models need to be consistent in the experiment.However,the parameters which control the grid field distance in the three models are inconsistent,so the grid field distance of the three models can only be kept as consistent as possible through many experiments.The grid cell firing effect obtained in the experiment is shown in Figure 15.The boxplot of the gridness score is shown in Figure 16.

FIGURE 1 2 Effect of gridness score change when the place field adjustment factors are different

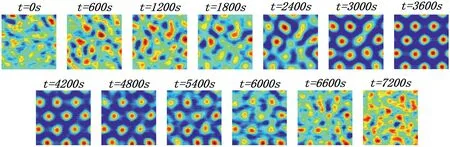
FIGURE 1 3 Effect of grid field change

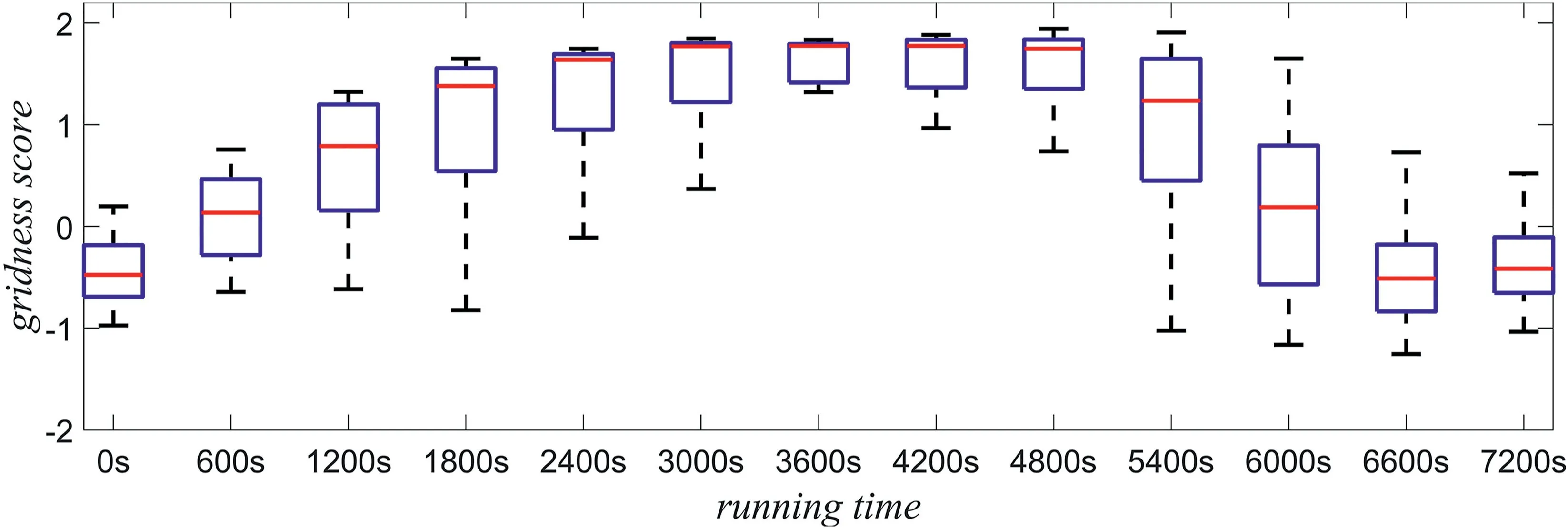
FIGURE 1 4 Effect of gridness score change

As it can be seen from Figures 15 and 16,when the robot moves at a uniform speed,all three models can show the standard grid field.With the increasing range of robot motion speed,the grid fields generated by the oscillatory interference model and the continuous attractor network model are gradually chaotic.However,the model in this paper can still maintain a stable hexagonal firing field.The experimental results show that our model is not sensitive to the non‐uniformity of robot motion speed,which verifies the robustness of the model.

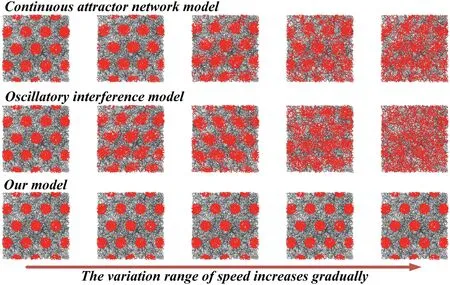
FIGURE 1 5 Grid cell firing effects of the three models

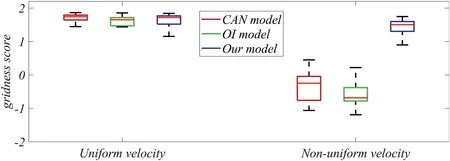
FIGURE 1 6 Gridness score of the three models under different conditions

5|DISCUSSION

This paper proposed a method for constructing the rat brain spatial cell firing model.The characteristics of the model are as follows:Firstly,the quadruped robot's position in the environment is calculated by obtaining the sensor information of the robot's limbs and IMU,simulating the estimation of the rat's motion state when only the self‐motion information is input.Then the theta cells which can generate VCO signals encode the location information and map them to the place cells through the neural network structure.After obtaining the place cells with single‐peak firing fields,the Hebb learning mechanism is used to adjust the neural network connection weights from place cells to grid cells.So that it can gradually form a regular hexagonal grid field throughout the whole space,simulating the change of the grid field.Compared with previous studies,there are the following differences and improvements.

1.At present,most research is based on data sets or wheeled robots.In this paper,a quadruped robot similar to the physiological structure of rats is used as the carrier to simulate the perception process of rats'self‐motion information,which is more bionic and persuasive.

2.Most spatial cells firing models collect signals first and then conduct offline experiments.Our model is an online learning model,which can show the change of the firing field in real time with the exploration of the quadruped robot.

3.The grid field self‐organising development model proposed in this paper is not sensitive to the nonuniformity of robot velocity distribution in the learning process.And the model allows learning on the basis of randomly activated episodic memory without recalling continuous motion trajectory segments.

6|CONCLUSION

The model in this paper is entirely based on the physiology research facts of spatial cells,and the model is verified by designing 3‐D simulation experiments.The experimental results show that with the robot exploring in a given space area,the model can not only simulate the path integration function of rats without visual input but also obtain the firing characteristics of place cells and grid cells consistent with physiological research.In view of the fact that the navigation tasks usually performed by mobile robots are carried out in the complex and unknown environment,the functions realised by the model in this paper are only to realize the path integration of the robot and the construction of the spatial cells firing model under the input of self‐motion information.

However,mammals usually combine various internal and external information to achieve their precise positioning in the environment.For example,physiological studies have found that rats use environmental information to quickly and accurately correct the cumulative error in the path integration process.Therefore,the cognitive and adaptive ability of our model to the complex unknown environment is much lower than that of mammals.The next research direction should be to construct the spatial cell firing model from the perspective of cognitive mechanism,using a variety of exogenous information(visual,smell,hearing,etc.)as input,and strive to make the robot gradually form and develop the cognitive ability of the environment in the process of interaction between the robot and the environment,thereby improving the robot's ability to adapt to the complex environment.

In summary,the research results in this paper lay a foundation for the robot navigation method that mimics the cognitive mechanism of the rat brain.It has crucial significance for research in robot navigation,environmental cognition,and map reconstruction.

ACKNOWLEDGEMENTS

This work was supported by the Natural Science Foundation of China(62076014,61773027)and the Natural Science Foundation of Beijing(4162012).

CONFLICT OF INTEREST

None.

DATA AVAILABILITY STATEMENT

Data sharing not applicable to this article as no data sets were generated or analysed during the current study.

ORCID

Yishen Liaohttps://orcid.org/0000-0003-0625-5816