含多个相干耦合人工原子的单模腔的输入输出特性*

郑赟杰 王晨阳 谢双媛 许静平 羊亚平

(同济大学物理科学与工程学院,教育部人工微结构材料重点实验室,上海 200092)

在以往的腔量子电动力学(QED)系统中原子气通常被处理成单个原子,从而得到诸如拉比劈裂、单光子阻塞等现象.受益于超导电路QED 的发展,超导量子比特(SQUID)可以被看成人工原子,它们之间通过LC 谐振子失谐的耦合会构成人工原子间的等效相干耦合.基于此,研究了具有相干耦合的多个人工原子对单模腔输入输出的影响,并从缀饰态的角度对透射谱进行了分析.结果发现包含多个相干耦合人工原子的单模腔,其透射谱与只含单个原子的腔显著不同,更重要的是透射峰的数目并不会随着人工原子数的增加而增加,最多只有3 个透射峰.为了解释这种透射谱的规律,应用全量子理论,计算了整个系统在不含耗散时单能量子情况下的本征值和本征态.原则上,有几个粒子,就会形成几个缀饰态,理论上就会出现几个透射峰.然而本文发现存在一些不包含光子成分的缀饰态,它们并不贡献透射峰.而原子数增多后会出现透射峰劈裂,这对应着能级避免交叉现象,本文从缀饰态角度进行了说明.从这些缀饰态的具体形式上很多都具有多体纠缠的性质.因此采用这样一种包含多个相干耦合人工原子的单模腔,将有利于构建多体纠缠态,在未来也可以通过透射率的变化,探知腔内多体纠缠态的形式.

1 引言

腔量子电动力学(quantum electrodynamics,QED)的研究历史可以追溯到1946 年提出的Purcell 效应—当原子处于一个与之共振的谐振腔时,其自发辐射的性质会发生改变,并受到腔的调制[1].1963 年,Jaynes-Cummings 模型的提出让腔QED 的研究进入了新的阶段[2],后来,研究者们在实验上将原子放置在镜子之间或空腔中,证实了腔可以大大抑制或增强原子的自发辐射,并完成了腔QED 的正式命名[3].1985 年,Gardiner 和Collett[4]提出了一种量子弥散理论,不仅考虑了存在热库时的输入与输出性质,而且发展出了量子朗之万方程,从而在已知输入统计量和其他相关参数的条件下,可以计算系统的输出.2007 年,基于前人的成果,Auffèves-Garnier 等[5]分析了含一个两能级原子的腔的输入输出关系,包括线性情况下由于原子存在而诱导的全反射,以及当输入场继续增强时,原子非线性吸收所产生的透射率变化等.在Alexia 等[5]研究的基础上,Xu 等[6,7]于2014 年和2017 年详细讨论了含有两能级原子的不对称单模腔的光学双稳态和输出光场的量子统计特性等.而这些工作主要基于单原子模型,即使实验上采用了原子气,其实验结果依然可以用单原子模型解释,这是因为由于热运动使原子之间的相干可以忽略[8].随着原子冷却技术的发展,原子的位置可以精确操控,因此对几个或多个原子在腔中的集体辐射行为开始进行研究,主要是讨论超辐射和亚辐射问题[9−12].在这些研究中,原子之间的相干性很重要,但从相互作用的角度看依然认为原子仅与腔模相互作用,原子之间的相干来自于与共同腔模的耦合.

电路QED 的发展,为拓展QED 的研究范围和实现普通腔QED 很难实现的研究对象创造了条件[13−15].最近Nie 等[16]使用三维集成电路来构建了SQUID(superconducting quantum interference device)的Su-Schrieffer-Heeger 模型,在他们的模型中SQUID 可以看成人工原子,相邻人工原子之间的相干耦合由失谐的LC 谐振器连接实现.同年,Nie 等[16]利用同类模型研究了拓扑带隙在边缘态量子操纵中的作用,基于拓扑量子比特阵列的奇偶特性,提出了一种光谱学方法来观察拓扑相变.将可调的弱探测场作为腔场,与原子阵列的不同本征态耦合,通过大失谐下的虚光子介导影响量子位的相互作用,主要目的是研究拓扑带隙对小型量子比特阵列的影响[17].基于Nie 等[16]利用三维集成电路构造的人工原子链系统,本文理论上将多个相干耦合的人工原子放置在微腔中,探讨原子间的相干耦合对输入输出关系尤其是透射谱的影响,以及与单原子-腔系统的不同之处.此外还利用全量子理论,即将共振的腔与原子阵列视为一个系统,计算其单光子缀饰态,解释了透射谱行为,并简单讨论了通过这样的相干耦合的多原子-腔系统制备多体纠缠态的可能性.

本文首先介绍了理论模型和透射谱的计算方法,展示了透射谱的计算结果,讨论了人工原子数目、原子间耦合、原子-腔模耦合、原子的自发衰减和腔损耗对透射谱的影响,并利用全量子的缀饰态理论对透射谱进行了解释,分析了一些特征透射峰对应的缀饰态,并对多体纠缠态进行了讨论.同时简单讨论了腔的耗散与原子的自发辐射对透射峰的影响.

2 理论模型和方法

考虑在一维单模微腔中存在规则排列的多个SQUID 人工原子,如图1(a)所示.圆点代表SQUID人工原子,它们可以看成两能级的全同粒子,其基态为|g〉,激发态为|e〉,跃迁频率为ωa.相邻圆点之间用粗细线相连,代表它们之间的最近邻相干耦合.人工原子间的相干耦合得益于量子芯片领域的进步,尤其是使用多层制造工艺的三维集成电路的产生与发展[13−15].在最近的工作中,如图1(b)所示,在三维超导电路中构造了人造原子SQUID 阵列,相邻人工原子通过LC 谐振器连接起来,LC 谐振器的频率被调制成与人工原子大失谐,从而在人工原子与LC 谐振器相互作用时,并不会有实光子传递到LC 谐振器上.通过对人工原子和LC 谐振器相互作用的哈密顿量做Schrieffer-Wolff 变换,获得人工原子间相干耦合的有效哈密顿量,其相干耦合强度可以通过系统参数进行调节[16].这里考虑偶数个人工原子组成的原子链,每两个原子为一组,分别用2n－1 和2n进行编号,n为组序号,组内原子间的耦合强度为tA,组间相邻原子间的耦合强度为tB.

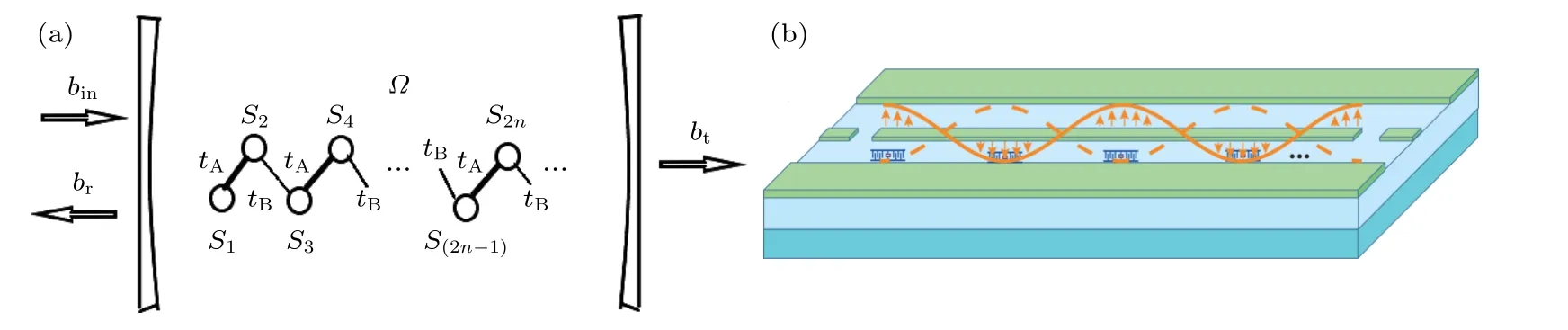
图1 (a) 存在输入-输出端口的Su-Schrieffer-Heeger 人工原子链-单模腔耦合系统示意图;(b)三维电路QED 示意图[16]Fig.1.(a) Schematic diagram of Su-Schrieffer-Heeger artificial atom chain-single-mode cavity coupling system with input-output ports;(b) three-dimensional circuit QED schematic diagram[16].

所有人工原子都与腔模耦合,其耦合强度为Ωi.此外腔模通过腔壁与左右两侧的电磁模库耦合.系统的哈密顿量(ℏ=1)可表示为

其中,a,bk和cl分别是腔模、输入端口(左侧)和输出端口(右侧)处电磁场模的湮灭算符,ωc,ωk和ωl为其相应的频率.Szi=(|e〉〈e|−|g〉〈g|)/2 与是第i个人工原子的算符.g1与g2分别是腔模和左侧与右侧电磁场模之间的耦合强度.n为原子组的序号,n≥1,原子序号i可用组号n表示.

方程(1)中第1 和第2 行代表人工原子链的哈密顿量,其中第1 项是自由人工原子的哈密顿量,第2 项是组内人工原子之间的相互作用,耦合系数为tA,第3 项是组间相邻人工原子间的相互作用,耦合系数是tB.第3 行第1 项是腔模光子的哈密顿量,第2 项是腔模与人工原子的相互作用,耦合系数是Ωi.第4 和第5 行的4 项依次代表左侧、右侧处电磁场模的哈密顿量以及腔模与左侧场模和右侧场模相互作用的哈密顿量.

这里主要讨论的是如果入射一束探测场,透射谱是怎么样的? 多个原子间的相干耦合是否会对透射谱产生影响,以及产生怎样的影响? 经过推导(详细过程见附录A),引入原子的自发辐射率γi和腔的损耗γcav,得到各算符的期望值a=〈a〉)微分方程为

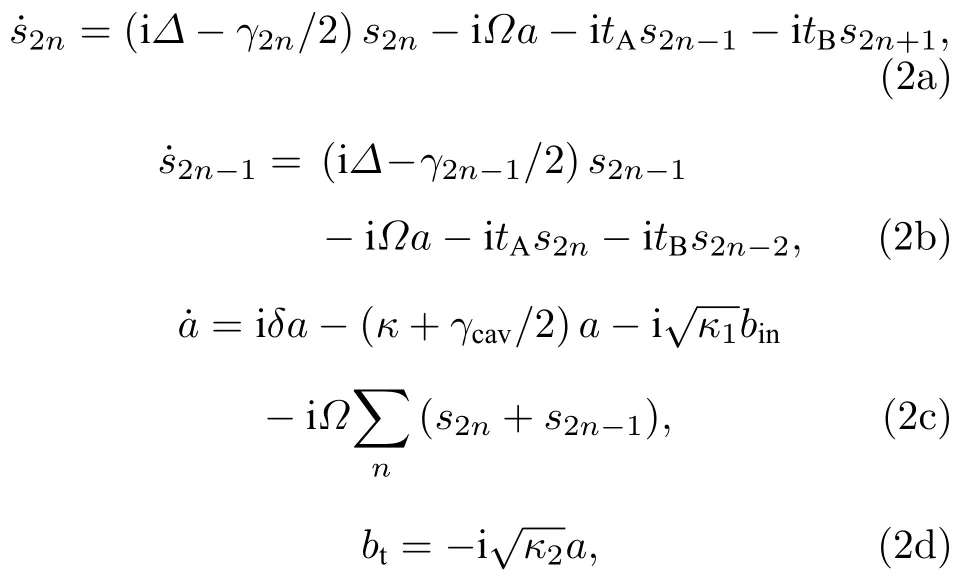
其中,∆=ωL −ωa和δ=ωL −ωc分别为入射场与人工原子以及与腔模之间的频率失谐.bin是单模入射场幅值,bt是透射场幅值.κ1和κ2与g1和g2相关,分别对应左侧和右侧腔镜的泄漏率,而κ=(κ1+κ2)/2.由于假定腔的品质因子很高,所以在后续计算中假定γcav≈0 .

在稳态情况下计算出各个期望值的稳态值,从而对于频率为ωL的弱入射场,得到了整个系统的透射系数:

而对应的透射率为

接下来讨论随着腔内人工原子数的增加以及各种耦合系数的改变,透射谱的性质.

3 透射谱的数值计算

针对以上模型,即含有偶数个人工原子的单模腔,本节将计算随着弱探测场频率变化时的透射谱,尤其是探索对透射谱造成影响的各项因素,包括腔内人工原子组数n、人工原子间耦合强度tA与tB,以及人工原子与腔模耦合强度Ωi,并找出其规律.在后续的讨论中,令人工原子与腔模共振,即ωa=ωc,左右腔壁的泄漏率相等,即κ=κ1=κ2,所有原子的自发辐射率一样,即γi=γ,并以耦合强度Ω0作为所有系数的单位.

对于只存在一个原子的单模腔,其透射谱的性质已经很清楚,即原子与腔模共振时会发生拉比劈裂,产生分列于腔模频率两侧的双透射峰,两个透射峰的频率差与原子-腔的耦合系数成正比.而原子衰减率γ以及腔模泄漏率κ的提高会使得透射峰的半高宽增宽,κ和γ对透射峰的具体影响将在第5节讨论.

3.1 腔内存在双原子的情况

首先考虑腔内存在一组两个人工原子的情况,原子间耦合系数为tA.在图2(a)中,令人工原子与腔模的耦合系数都相等,即Ω1=Ω2=Ω0,计算透射谱随着人工原子间耦合系数tA的变化.从图2(a)可见,当tA=0 时,两个人工原子相当于一个大原子,透射峰为典型的拉比劈裂双峰.逐渐增大tA,透射峰逐渐变成不对称的双峰,且蓝移透射峰(δ >0)的峰值要小于红移透射峰(δ <0)的峰值,同时红移的透射峰的中心频率逐渐趋近于δ=0 .当tA>5Ω0时,蓝移透射峰消失,只剩下红移透射峰,即双峰透射谱变成单峰透射谱.继续增大tA,红移的单峰透射率逐渐增大并趋于1,且透射峰的中心频率趋向于腔的共振频率.这可以理解为当tA≫Ω0时,两个人工原子相互耦合,形成缀饰态,但缀饰频率与原有频率失谐很大,也与腔模失谐,对腔模来说相当于没有原子,从而产生了中心频率在腔模频率的透射峰.

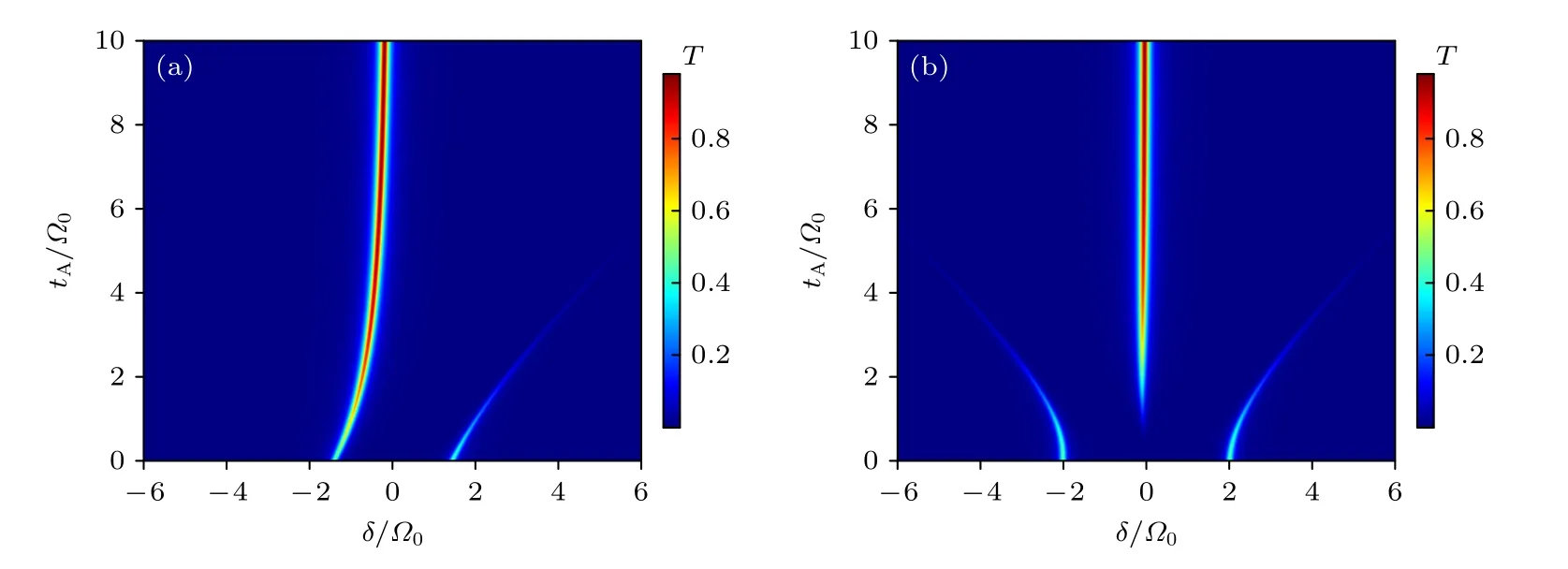
图2 腔中存在一组共两个人工原子时,透射率随入射场与腔模失谐 δ 和原子间耦合 tA 的变化 (a)双原子与腔模的耦合强度一致,Ω1=Ω2=Ω0;(b)双原子与腔模的耦合强度不同,Ω1=2Ω0,Ω2=0.1Ω0,采用参数κ=γ=0.1Ω0Fig.2.In the case of a set of altogether two artificial atoms in the cavity,transmittance varies with the detuning δ between incident field and cavity mode and interatomic coupling tA : (a) The coupling strength of diatoms and cavity mode is consistent,Ω1=Ω2=Ω0;(b) the coupling strength between diatoms and cavity modes is different,Ω1=2Ω0,Ω2=0.1Ω0,the parameters are κ=γ=0.1Ω0 .

在图2(b)中讨论了两个人工原子与腔模的耦合强度不同,即Ω1=2Ω0,Ω2=0.1Ω0时的透射谱随人工原子间耦合系数tA的变化.当tA=0 时,虽然两个人工原子与腔模的耦合系数不同,但依然可以看成一个等效原子,所以透射谱仍呈现为对称的拉比劈裂双峰结构.随着tA开始增大,双峰的峰值逐渐降低.当tA=0.7Ω0时,在接近失谐δ=0 的频率处出现了新的透射峰.继续增大tA,两侧的双峰峰值继续降低,而中央透射峰峰值变大,呈现出三峰结构.对比图2(a)和图2(b)发现,当tA>5Ω0时,与图2(a)类似,图2(b)也由三峰结构转变为单峰,且主峰频率趋向于腔的共振频率.

由以上结果可以确认: 人工原子间的相干耦合对腔原子系统的透射谱会产生很大影响.且人工原子与腔模的耦合系数也会对透射谱的形状产生影响.从上面的讨论可知,对于腔中存在两个原子的情况,最多可以存在3 个透射峰,那么继续增加相干耦合的原子数目,透射峰的数目是否会继续增加呢?

3.2 腔内存在4 个人工原子的情况

现在考虑腔内存在两组4 个人工原子的情况.固定组内原子间耦合系数tA=Ω0,计算了透射谱随着组间原子耦合系数tB的变化,如图3(a)所示.当tB=0 时,两组原子缺乏关联,近似于腔内双原子的情况,对应于图2(a)中tA=Ω0时的双峰结构.但随着tB的增大,红移透射峰(δ <0)的峰值基本不变,对应频率轻微偏向腔的共振频率,而蓝移透射峰(δ >0)峰值逐渐减小,并逐渐远离共振频率.当tB接近于 2Ω0时,在δ=0 附近出现新的透射峰,继续增大tB,其峰值增大并略微蓝移.

而图3(b)则固定原子间耦合为tA=Ω0和tB=3Ω0,展示了原子与腔模耦合强度Ω对透射谱的影响.若Ω=0,原子不与腔相互作用,入射场仅与腔模共振,则在腔的共振频率处形成单峰透射谱,最大透射率接近1.随着Ω的增大,原本的透射峰分裂为红移、蓝移的双峰.红移透射峰的峰值接近0.8 且较为稳定,但对应频率不断红移;蓝移透射峰的频率接近共振,但峰值迅速降低,当Ω >5Ω0时峰值忽略不计.与此同时,当Ω >Ω0时,在频率δ=3.5Ω0处出现新的透射峰,随着Ω的增大,其峰值增大并线性蓝移.

图3 的结果再次验证了: 在4 原子条件下,透射峰的数量及对应频率可以通过原子与腔模耦合强度Ω和原子间耦合强度tA,tB来调控,但最多只存在3 个透射峰.

3.3 腔内存在6 个人工原子的情况

当腔内存在3 组共6 个人工原子时,与前文类似,透射谱的透射峰数目并没有增加,最多只存在三峰,因此选择一些代表性的计算结果加以展示.

如图4(a)所示,固定组内原子间耦合系数tA=Ω0,计算了透射谱随组间人工原子耦合系数tB的变化.透射谱变化的过程整体与图3(a)一致,这说明在采用相同参数的情况下,原子组数从2 组增加到3 组基本不会改变透射谱的演化规律,tB对透射谱的影响不会随着原子数的增加发生质的改变.图4(a)与图3(a)只存在一些细节上的差异,例如透射峰对应频率与共振频率的失谐加大,中央透射峰出现时对应的tB稍大,以及红移透射峰在tB=4Ω0附近出现了较为明显的劈裂现象,如图中红框所示.

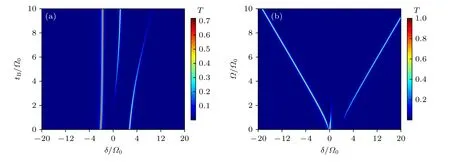
图3 腔中存在两组共4 个人工原子时,(a) 透射谱随原子间耦合强度 tB的变化,Ω=2Ω0 ;(b) 透射谱随原子与腔模耦合强度Ω的变化,tB=3Ω0 .采用参数为tA=Ω0,κ=0.2Ω0,γ=0.1Ω0Fig.3.(a) In the case of two sets of altogether four artificial atoms in the cavity,transmission spectrum varies with the interatomic coupling intensity tB ,Ω=2Ω0;(b) The transmission spectrum varies with the coupling strength Ω between the atom and the cavity mode,tB=3Ω0 .The parameters are tA=Ω0,κ=0.2Ω0,γ=0.1Ω0 .

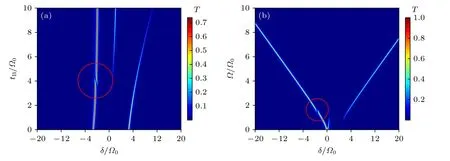
图4 腔中存在3 组共6 个人工原子时,(a) 透射谱随原子间耦合强度 tB的变化,Ω=2Ω0 ;(b) 透射谱随原子与腔模耦合强度Ω的变化,tB=3Ω0 .采用参数为 tA=Ω0,κ=0.2Ω0,γ=0.1Ω0,红圈内为本文定义的劈裂Fig.4.(a) In the case of three sets of altogether six artificial atoms in the cavity,transmission spectrum varies with the interatomic coupling intensity tB ,Ω=2Ω0;(b) the transmission spectrum varies with the coupling strength Ω between the atom and the cavity mode,tB=3Ω0 .The parameters are tA=Ω0,κ=0.2Ω0,γ=0.1Ω0 .The splits defined in this article are circled in red.

而图4(b)则固定了原子间耦合为tA=Ω0和tB=3Ω0,展示了原子与腔模耦合强度Ω对透射谱的影响,结果与图3(b)展示的透射谱演化基本一致,说明了随着原子组数的增长,原子与腔模耦合强度Ω对透射谱的影响几乎不变.图4(b)与图3(b)之间只存在细节上的不同,例如透射峰对应频率与共振频率的差异加大,中央透射峰随Ω的衰减加快,以及红移透射峰在Ω=1.5Ω0附近出现了较为明显的劈裂现象,如图中红框所示.

此外也计算了4 组共8 个原子和5 组共10 个原子的情况,发现随着原子组数的增加,透射谱的性质与腔中存在2 组共4 个原子基本一致,因此不做赘述.然而需要注意的是,在图4 中红圈内出现的透射峰劈裂并非孤例,实际上它多有发生,但由于劈裂的细微和系统损耗对透射峰半高宽的影响有时难以在图片中显著呈现.如何解释上述透射谱的变化规律和透射峰的劈裂,则需要从全量子的角度进行分析.

4 用缀饰态理论解释透射谱性质

本节根据全量子理论[18],通过缀饰态能级和各能级的平均光子数来解释透射谱的性质以及透射峰的劈裂现象.在分析中还发现各透射峰对应的缀饰态都是一系列腔内纠缠态,这将有利于多体纠缠态的制备.

因为本文研究的是弱光入射时的输入输出问题,属于线性区域,在转换成相应的全量子理论时,则是忽略腔的泄漏以及原子的自发辐射率,仅仅将腔模和原子链看成一个整体,计算其本征值和本征态[19,20].由于对应于弱光入射时的输入输出问题,则其希尔伯特空间的选取仅仅考虑单量子空间.这种单量子空间仅考虑只存在一个激发子的原子-腔直积态,即其中第1 个态表示原子全部处于基态,但腔中存在一个光子;第2 个态表示腔中没有光子,但第i个原子处于激发态.详细推导见附录B.

通过对角化得到的本征态是以上直积态的相干叠加态.若外加探测场的频率与本征态的本征频率一致,就能激发这个本征态.理论上对于相互作用的多体系统,如果有几个客体,那么就会存在几个本征态.但是否产生透射峰,则需要根据(2d)式来判定.从(2d)式可见,透射光幅值bt与腔内光场幅值a成正比,因此要想得到透射峰则需要该本征态中包含光子成分,因此在对角化后,对每个本征态都计算其平均光子数,如果平均光子数不为0,则对应透射峰,且平均光子数越大,透射率越高.

首先,采用与图2(a)相同的参数,计算腔中存在两个人工原子时的本征值和本征态.缀饰态本征值随原子间耦合强度tA的变化如图5(a)所示.可见在任何参数下都存在3 个本征态,按照本征值从小到大分别用红、绿、蓝三色代表不同的本征态.对比图2(a)中的透射峰的中心频率,发现其与图5(a)中的两个本征值对应.此时有3 个本征态,但只存在两个透射峰.为了解释该现象,在图5(b)—(d)中分别计算了3 个本征态的原子占居数〈Sz1〉,〈Sz2〉和平均光子数〈a+a〉,并用虚线、点线、实线表示.由图5(a)可见,本征态1 和本征态2 的本征值在tA=Ω0处存在避免交叉点,已用红框圈出,图5(e)为避免交叉点的放大图.而相应地,图5(b)中本征态1 的平均光子数在此处突变为0,图5(c)中本征态2 的平均光子数在此处由0 突变到图5(b)中变化前的值.严格来说,这是两个存在相互作用的本征态能级进行了平均光子数的突变交换.需要注意的是,虽然存在3 个本征态,但是对于某一参数,只有两个本征态具有非零的平均光子数,其中图5(d)显示本征态3 始终具有非零的平均光子数,且随着tA的增大近乎指数衰减,这对应于图2(a)中蓝移的透射峰峰值随着tA快速下降.对于本征态1 和2,当tA<Ω0时,只有本征态1 具有非零的平均光子数,当tA>Ω0时只有本征态2 具有非零的平均光子数,平均光子数随着tA的增大逐渐趋于1,这对应着图2(a)中的红移透射峰峰值逐渐增大.因此,利用单量子缀饰态很好地解释了透射峰的性质.

图5 腔内双原子条件下,(a)缀饰态的能级;(b)—(d)各能级对应的原子占据数 〈Szi〉与腔内平均光子数 随 tA 的变化;(e)避免交叉点放大图.其他参数为 Ω1=Ω2=Ω0 ;按照本征值从小到大分别用红、绿、蓝三色代表不同的本征态Fig.5.In the case of two atoms in the cavity,(a) the energy levels of the dressed states;(b)–(d) the corresponding atomic excitation probability of each energy level and the average number of photons in the cavity change with tA ;(e) a larger version of avoid crossing points.The parameters are Ω1=Ω2=Ω0 .The eigen states are represented by red,green,and blue in order of eigen values from smallest to largest.

此外,缀饰态还存在更多的应用.系统的透射峰与平均光子数不为零的缀饰态能级相对应,那么只要调整入射光的频率,使其与透射峰对应,就能通过计算缀饰态,来确认腔内原子与光场的状态.如果使用恰当的参数,再选择特定的透射峰,就能获得特定的纠缠态.例如,如图5(d)所示,选定本征态3,对应于图2(a)的蓝移透射峰,当原子间耦合tA=1Ω0时,腔内原子与光场的状态为

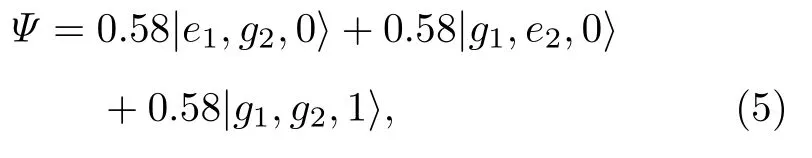
这相当于一个三粒子的最大纠缠态.

四原子的情况与两原子的情况类似,接下来详细分析腔内光子与3 组共6 个人造原子形成的缀饰态,为了便于与前文对比,采用与图4(a)相同的参数.如图6 所示,绘制了腔内存在六原子时,缀饰态能级图随原子间耦合强度tB的变化,不同颜色分别代表不同的能级,并依照本征值的大小编号,能级大小与图4(a)的失谐δ相对应,而不同线型分别代表6 个人造原子的激发概率和腔内的平均光子数.与此前类似,本征态1 与2、本征态2 与3 的能级曲线分别在tB=3.15Ω0,tB=4Ω0处出现了避免交叉点,已用红框圈出,图6(i)和图6(j)为避免交叉点的放大图.分别对比图6(b)和图6(c)、图6(c)和图6(d),可以发现本征态1,2 和3 在避免交叉点附近存在耦合,同样都进行了光子数和原子态的交换.本征态1,2 和3 共同对应图4(a)的红移透射峰;本征态4 和6 的平均光子数始终接近0,对透射无贡献;本征态5 对应于接近共振的透射峰;而本征态7 对应于图4(a)中逐渐降低的蓝移透射峰.综上所述,图6 所画缀饰态与图4(a)的透射谱同样吻合.

图6 腔内六原子条件下,(a)缀饰态的能级;(b)—(h)各能级对应的原子占居数 〈Szi〉与腔内平均光子数随 tB 的变化;(i),(j)避免交叉点放大图.采用参数为 Ω=2Ω0,tA=Ω0 ;不同颜色分别代表不同的能级,并依照本征值的大小编号Fig.6.In the case of six atoms in the cavity,(a) the energy levels of the dressed states;(b)–(h) the corresponding atomic excitation probability of each energy level and the average number of photons in the cavity change with tB ;(i),(j) two larger versions of avoid crossing points.The parameters are Ω=2Ω0,tA=Ω0 .Different colors represent different energy levels and are numbered according to the magnitude of the eigenvalue.

特别地是,对于tB=4Ω0时本征态2 与3 的避免交叉点,在图4(a)的透射谱中出现了小小的劈裂,而本征态1 和2 同样存在能级避免交叉现象,却无法在图4(a)中观察到明显的劈裂.对比了图6(b),(c)和(d)中本征态1,2 和3 的各组分分布,发现在tB=3.15Ω0附近两个态的平均光子数是突变的,而在tB=4Ω0附近两个态的平均光子数是连续变化的.因此,可认为当两个缀饰态的本征频率在某一参数下交叠,但其各自的平均光子数在这一参数附近并没有发生突变交换,那么在能级出现避免交叉现象的同时,透射谱中也将展现出明显的劈裂现象.而图5(a)中本征态1 和2 在tA=Ω0处避免交叉,以及图6(a)中本征态1 和2 在tB=3.15Ω0的避免交叉,他们对应的平均光子数在这两个参数附近都出现了突变交换,因此虽然这些本征态之间存在相互作用,但是并没有在透射谱中产生明显的劈裂.

避免交叉的概念在核物理、原子物理等诸多领域中十分常见,它存在不同的定义,而我们根据参考文献[21],从动力学角度进行解释.需要注意一点,本征态在避免交叉点前后会交换特征[21],在图6中的表现为两个本征态的原子占居数〈Szi〉 和平均光子数〈a+a〉都出现交换,而平均光子数的连续交换则导致了图4(a)中红移透射峰的劈裂现象.

腔内存在3 组共6 个原子的情形下,依旧可以采用适当的参数,并选择特定的透射峰,从而制备特定的纠缠态.例如,如图6 所示,选定能级3,对应于图4(a)的红移透射锋,当原子间耦合tA=8Ω0时,腔内原子与光场的状态为

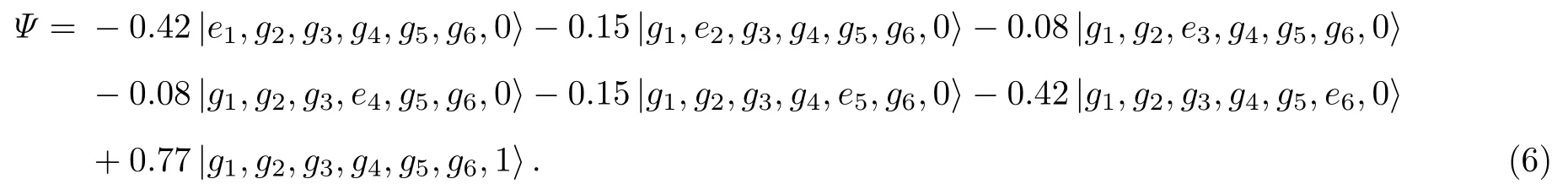
此时,平均光子数较高,而人工原子链中处于首尾对称位置的人工原子激发的概率幅一致,且越靠近原子链中心,其激发越受抑制.

5 原子自发辐射和腔的损耗

接下来讨论原子自发衰减γ和腔的泄漏率κ对透射谱的影响,仅选取2 组共4 个人工原子的情形加以介绍.

如图7 所示,原子自发衰减γ和腔的泄漏率κ对透射峰的中心频率基本没有影响,但会明显地改变透射峰的半高宽和透射率的大小.对比图7(a)与图7(b),可发现透射峰的半高宽随着原子自发衰减γ的增大而增宽,但透射率却出现了明显的下降.再对比图7(a)与图7(c),虽然腔的泄漏率κ对透射峰峰宽的影响与原子的自发衰减类似,但透射率反而大幅增长,这一点结合模型很好理解,κ代表了腔端口处的泄漏率,所以κ的增大有利于光的透射.需要注意的是,透射峰半高宽的增大容易导致相邻本征态能级的透射峰合并,结合前文,这会使透射峰劈裂现象有时难以观察到.

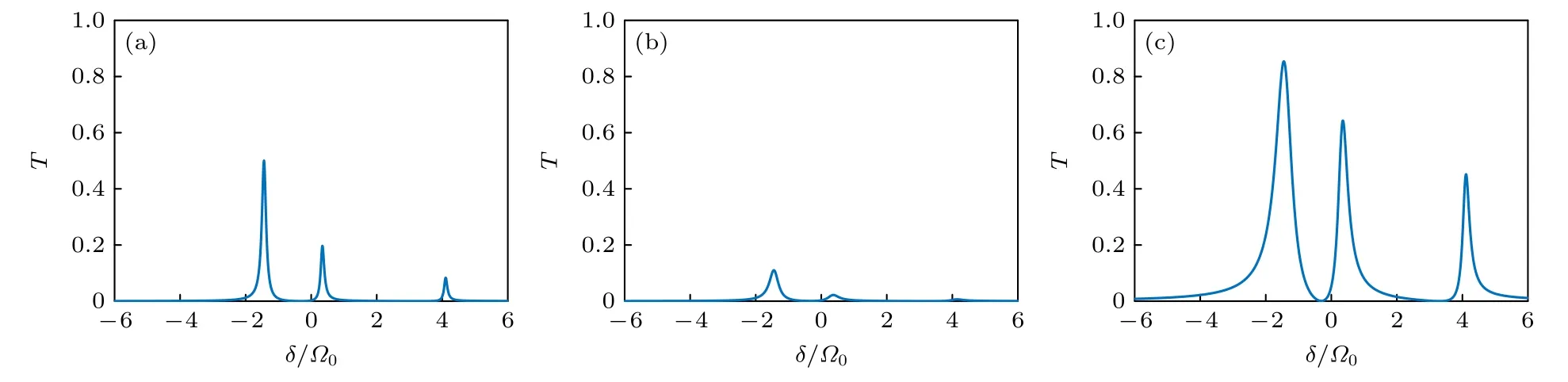
图7 (a) κ=γ=0.1Ω0条件下的透射谱;(b)原子自发衰减增大后的透射谱,κ=0.1Ω0,γ=0.5Ω0 ;(c)腔的泄漏率增大后的透射谱,κ=0.5Ω0,γ=0.1Ω0 .采用参数为Ω=Ω0,tA=Ω0,tB=3Ω0Fig.7.(a) Transmission spectrum under κ=γ=0.1Ω0 ;(b) the transmission spectrum after the increase of atomic spontaneous attenuation,κ=0.1Ω0,γ=0.5Ω0;(c) the transmission spectrum after the increase of leakage rate of cavity,κ=0.5Ω0,γ=0.1Ω0.The parameters are Ω=Ω0,tA=Ω0,tB=3Ω0 .

此外发现透射峰在部分频率下受到抑制,呈现出尖锐的非对称的光谱线形,出现Fano 共振现象.以图7(c)为例,3 个透射峰都不遵守对称的洛伦兹线形,在δ=0和δ=4Ω0附近,透射峰受到的抑制尤为明显.这是入射光频率作为连续态的背景,而腔内缀饰态呈离散态的响应,二者相干耦合所导致的非对称的Fano 共振光谱[22].

可以总结出,原子自发衰减γ和腔的泄漏率κ对透射谱的影响规律:γ和κ对透射峰的对应频率无明显影响,但会显著改变透射峰的半高宽和透射率的大小.峰的半高宽随着原子的自发衰减γ或腔的泄漏率κ的增大而增大,而透射率随γ的增大而减小,随着κ的增大而增大.

6 总结

本文研究了内含相干耦合人工原子的单模腔在线性区域内的透射谱性质,并从单光子缀饰态角度进行了解释.在光子透射的线性区域,单模腔内至多存在一个光子,由缀饰态理论可以猜想透射峰数目最多为2n+1 个(n为原子组的序数),此结论在单、双原子的情况下得到验证.但腔内原子数更多时并不遵循以上规律,最多只有3 个透射峰,这是因为有些缀饰态中没有光子成分,不贡献透射峰.透射峰对应的频率可以利用原子与腔模耦合强度和原子间耦合强度加以调控,而原子的自发衰减和腔的损耗对透射峰的对应频率无明显影响,但会显著改变透射峰的峰宽和透射率的大小.虽然本文考虑的SSH 链都以2 个人工原子为一组,但是人工原子数为奇数的情形也做过验证,在模型、公式、图像上都与偶数个原子的情形存在些微区分,不便赘述,但二者遵循相同的演化规律,本文的主要结论仍然适用.

基于本工作,将相干耦合的多原子系统与腔模耦合,通过输入输出关系,可利用透射谱测定原子链的耦合、原子与腔模的耦合等变量.实际应用中,可以利用透射谱检测腔的品质因子、端口的衰减率及原子的自发辐射常数.单量子缀饰态的计算可以解释透射谱的演变规律,发现一些透射峰与缀饰态一一对应,而这些缀饰态就是一些特殊的多体纠缠态,而纠缠态中各组分的比重也可以通过调控原子链的耦合、原子与腔模的耦合和入射光的频率等变量来调节.对于如何利用现有结果进行多体纠缠态的制备,SSH 链的拓展以及本模型在拓扑领域的应用,我们将在后续工作中进行细致和系统的研究.

附录A: (2a)—(2d)式的推导

针对系统的哈密顿量方程(1),首先根据海森伯方程

定义从端口1 入射的入射场算符bin为

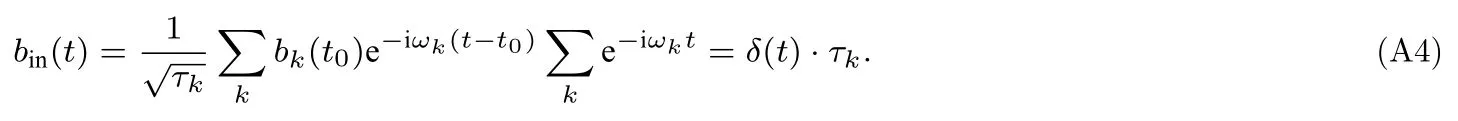
将(A3)式对所有模式k做累加,利用(A4)式,同时对有关腔模湮灭算符a的积分做马尔科夫近似,可得

最后,可以得到入射场算符bin与反射场算符br、透射场算符bt之间的关系[4−7](见图1(a)):

其中,κ1=g12τk,κ2=g22τk为端口1 和端口2 处的腔模泄漏率.

结合原子的自发辐射率γ、腔模的耗散率γcav,以及定义腔模通过两个端口的总泄漏率κ=(κ1+κ2)/2,并令入射探测场bin为频率为ωL的单色场,得到了包含各种耗散的系统的海森伯方程:

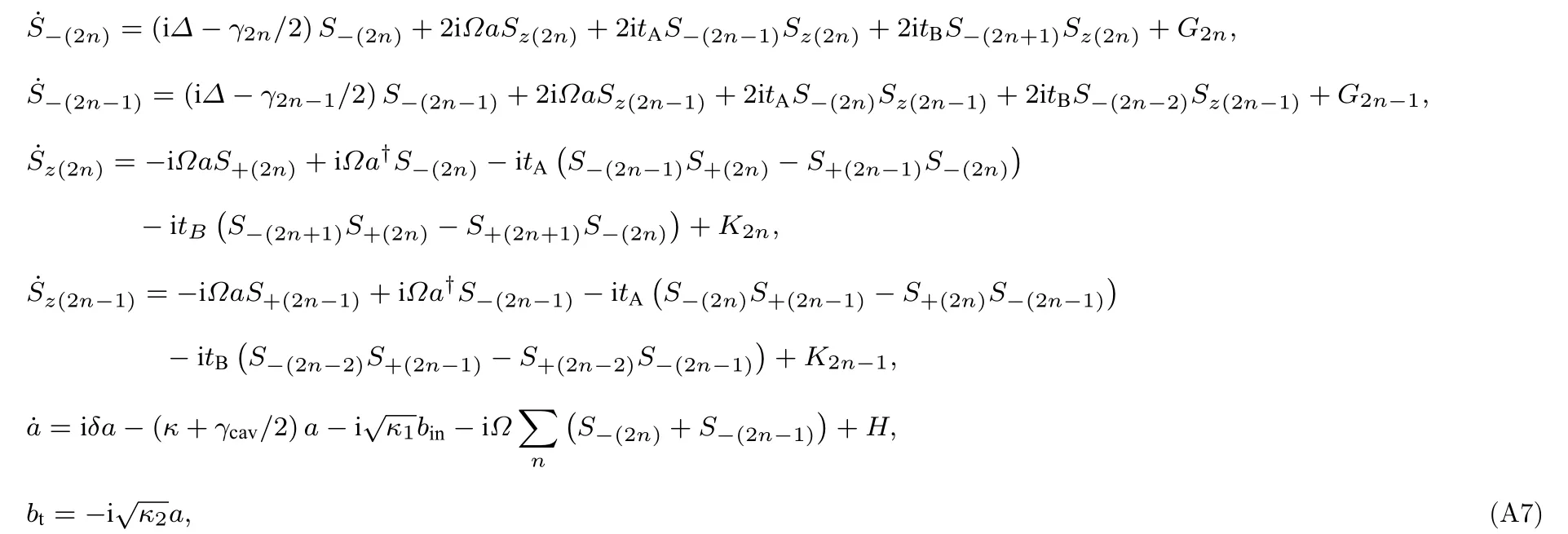
对于这种输入输出问题,采用平均场近似,利用算符的期望值来代替算符,如s=〈S−〉和场的振幅a=〈a〉,bin=〈bin〉,bt=〈bt〉,同时假定是弱场输入,从而对于所有人工原子可以设=−1/2,这样就可以在稳定输入的情况下,计算透射和反射问题[19,20].

最终得到的Heisenberg-Langevin 方程为

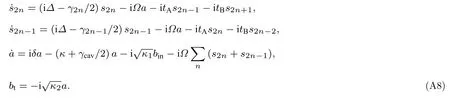
附录B: 缀饰态的推导

当腔内SSH 链存在n组原子(2n个全同粒子),且腔内量子数为1 时,可能存在2n+1 个本征态(称为裸态),具体为

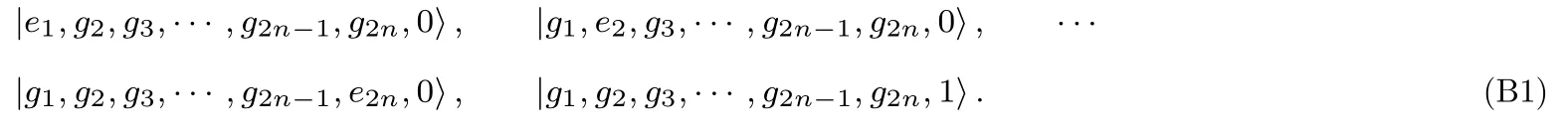
因为缀饰态只取决于单模腔和腔内SSH 链构成的系统,所以计算缀饰态时,须要将(1)式内的总哈密顿量简化为

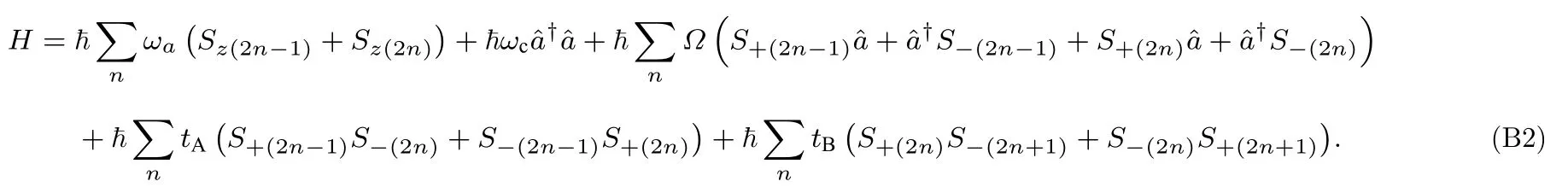
将等式(B2)的总哈密顿量分别作用到各个裸态上,求出在裸态基下,总哈密顿量的矩阵元,并整理成矩阵形式:

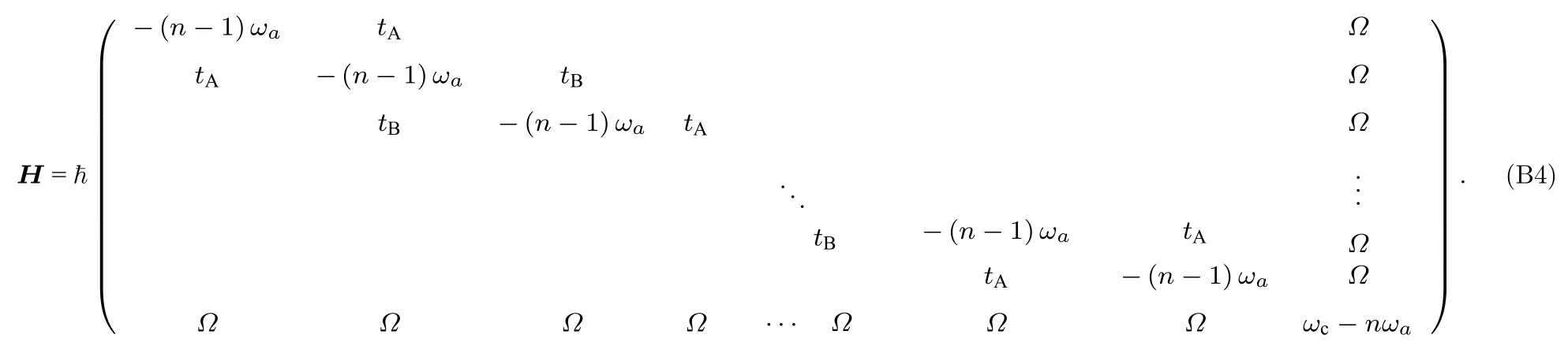
通过(B3)式,可以求解缀饰态的本征值(能级),以及各能级对应的缀饰态的表达式.