基于二阶Markov模型的改进相对熵测试充分性准则
张 凡,李福川,陈丽容,吕中凯
(1.中国航天科工集团第二研究院 七〇六所,北京 100854;2.中国人民解放军 93160部队,北京 100166)
0 引 言
近年来,国内外软件测试充分性技术的研究方向主要集中在测试充分性模型,测试充分性准则、测试用例自动生成等方面,其中软件测试充分性准则是研究软件测试充分性的基础和前提,因为软件输入空间是无穷性的,测试空间是有限的,不可能对软件进行穷举测试,只能在满足一定的充分性准则的前提下进行相对充分的测试。Markov过程因其具有对动态随机过程刻画的先天优势,被众多国内外学者用于描述软件测试模型和软件测试充分性准则的研究,并取得了一系列的研究效果[2],逐渐成为软件测试充分性研究方向的重要热点[1]。
本文首先介绍了Markov链模型的定义及其特性,对现有的基于Markov模型的软件测试充分性判定准则进行研究分析,针对现有方法可能出现的“早熟”问题等缺陷,提出了一种基于二阶Markov模型的改进相对熵软件测试充分性准则。通过数值实验对比验证了充分性评价指标的有效性,实验结果表明,该充分性判别准则能较为准确地评估测试用例集对单元测试的测试充分程度,有效地解决了测试用例生成过程过早收敛的问题、增强了测试充分性判定的稳定性。
1 Markov链模型概述
Markov链模型最早是由Andrey. Markov于1906年提出的,它是基于统计理论且可以描述软件使用情况的一种统计模型,Whittaker于1994年将Markov链模型用于软件统计测试[3]。由于Markov链模型是具有迁移概率属性的一种有限状态机,软件在状态之间的转换过程中存在着转移概率,该转移概率可以通过相邻的前序状态推算出来,这个特性称为“无后效性”。同时,Markov链模型不仅能够依据各个状态之间的状态转移概率自动生成测试用例,而且可以通过充分性测试对软件的测试充分程度进行评估[4]。
Markov链模型是表示软件从起始运行到结束运行状态的随机过程,它可以用带状态转移概率的迁移图或者随机迁移矩阵来描述软件的使用[5]。一阶Markov链模型可以用一个四元组Markov来进行形式化表述[6]
Markov=〈S,T,E,σ〉
(1)
式中的符号和解释见表1。
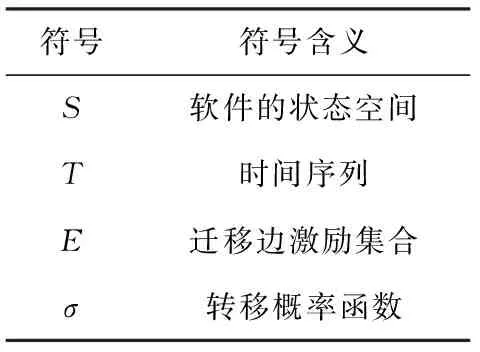
表1 一阶Markov链模型的四元组表示
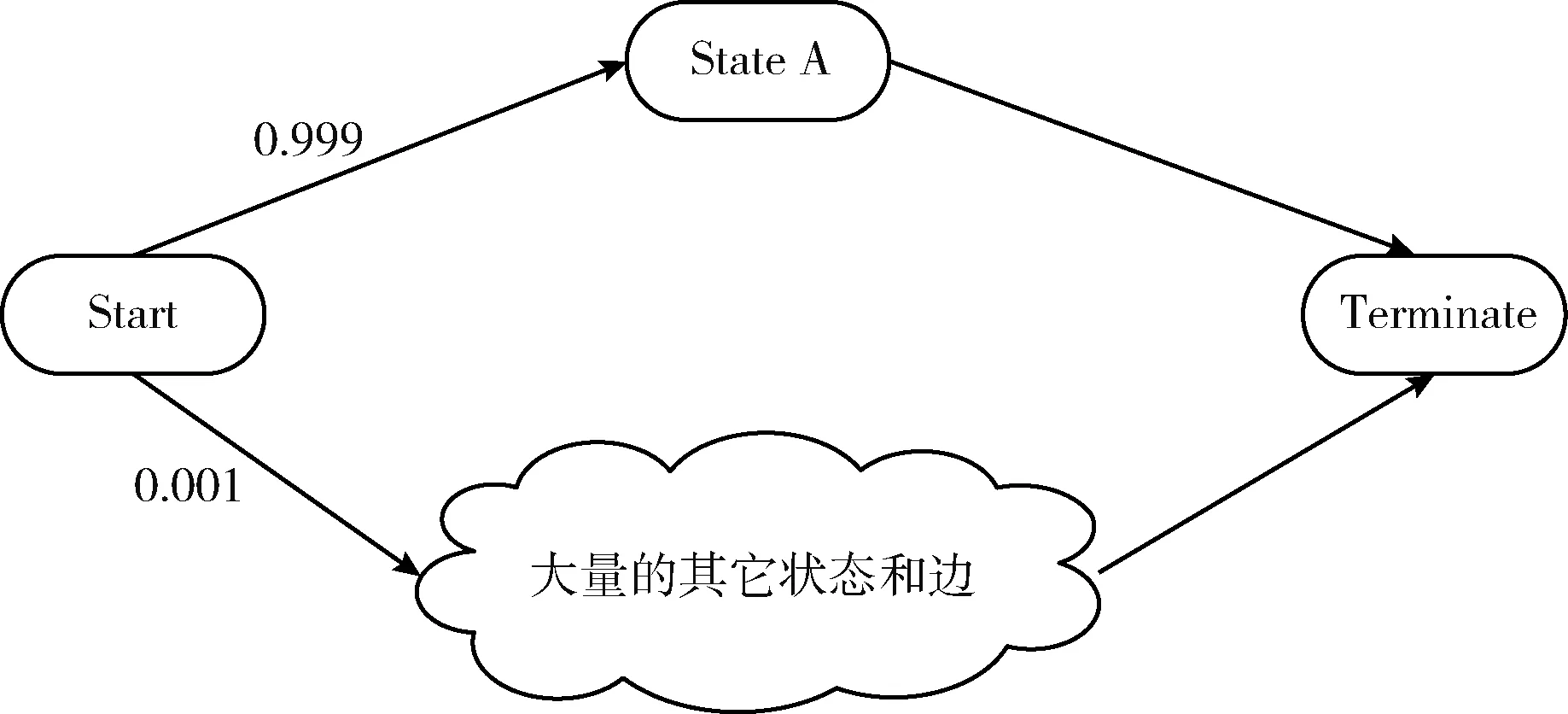
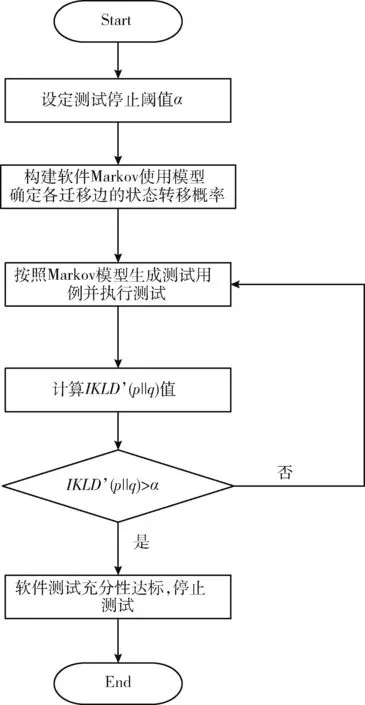
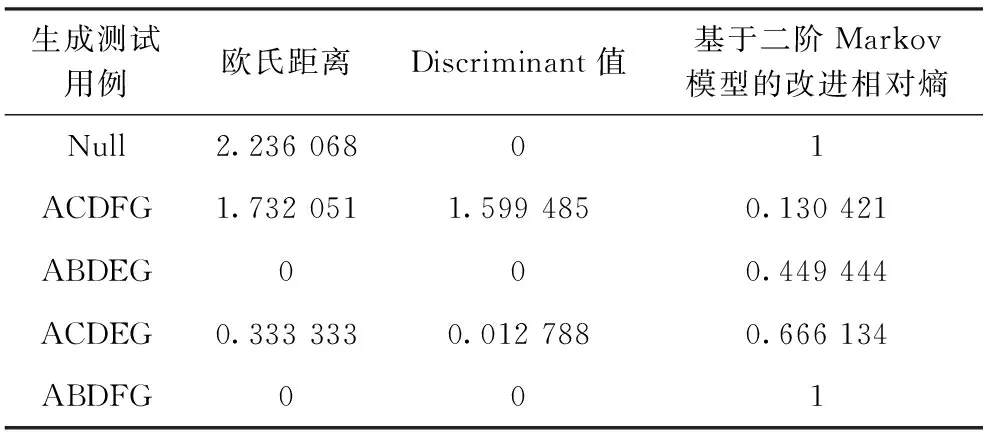
任一Markov链模型的状态集合S可表示为:S={S1,S2,…,SN}。 令S1为软件的初始状态,SN为软件的结束状态,且S1∈S,SN∈S, 状态Si转移到状态Sj(1≤i≤N, 1≤j≤N) 的边激励信息可以表示为eij,一步转移概率σ(i,j) 可以表示为pij。设随机过程为 {X(t),t∈T}, 其中时间序列T={t1,t2,…,tN}, 且t1 P{X(tN)=SN|X(tN-1)=SN-1,…,X(t1)=S1}=P{X(tN)=SN|X(tN-1)=SN-1} (2) 无后效性在Markov过程中的定义可理解为时刻tN的状态只与前一个时刻tN-1有关,而与过去时刻t1,…,tN-2都没有关系,且条件概率P{X(k)=Sj|X(l)=Si}=pij定义为Markov过程中从状态Si到状态Sj的转移概率分布。设P表示转移概率pij所组成的一阶转移概率矩阵,对于N个状态,一阶转移概率矩阵P为N*N的矩阵,其数学定义表示如下 (3) 对于齐次Markov链,称式(4)定义的条件概率 Pij(m,m+n)=P{X(m+n)=Sj|X(m)=Si} (4) 为Markov链模型在时刻m到时刻m+n从状态Si到状态Sj的n步转移概率,记为P(n)。当n=1时即为Markov链的一步转移概率。Kolmogorov在前人的基础上研究了离散参数Markov链的转移规律[7]。设pij(k)表示状态Si经k步转移到状态Sj的概率,则有 (5) 称为Chapman-Kolmogorov方程(简称C-K方程),它是齐次Markov链模型中计算n步转移概率的重要依据[8]。 基于软件的Markov链模型,在测试执行过程中可以通过人工或者自动生成无限数量的测试用例,所以理论上软件测试过程可以不受限制地进行。但由于人力和物力等开销的限制,所以有必要在适当的时间点停止执行测试过程,这就是测试充分性判别准则所需考虑的内容[9]。同时,基于Markov模型的测试充分性准则适用于黑盒测试,更注重评估需求实现的充分程度,因此,当代码不可见时,便可选择基于Markov模型的测试充分性准则来对系统的测试充分程度进行评估。 在Markov使用模型中,测试的充分性是通过比较测试过程中使用链和测试链的差异程度来衡量的[10]。Markov初始使用模型被称为使用链,而测试链是通过执行测试过程从使用链中产生的。测试之初首先用一个初值为0的计数器来替换使用链中各迁移边所对应的状态转移概率。依次执行所有的测试用例,每当一个测试用例覆盖了其中的某条迁移边时,对应于该迁移边的计数器就递增1,并根据每条边相应的计数器的值所占比例计算出该边的相对转移概率,从而形成一个测试链。如果测试空间和预期使用空间的差异度满足规定的阈值,那么通过测试空间得出的测试充分性就能代表在实际应用过程中的测试充分性,即认为软件测试已充分执行了[11]。 目前现有的基于Markov链模型的软件测试充分性准则,主要依据计算欧氏距离(Euclidean distance[12])和Kullback判别式(Kullback discriminant[13])对测试链和使用链的吻合情况进行定量分析。 欧氏距离是一种常见的距离度量方法,常用于对有向图或图像之间的差异程度进行度量。其表达式如下 (6) Markov使用模型可以看作是一个包含状态转移概率的迁移边组成的有向图,因此对测试链和使用链吻合性的度量,可以转化为对两个有向图中转移概率之间的差异程度的度量,进而根据差异的大小来衡量测试的充分性。因此可以用欧氏距离来衡量两者之间的差异,其计算方法表述如下 (7) 式中:ui,j表示使用链中状态Si到状态Sj的转移概率,ti,j表示测试链中状态Si到状态Sj的转移概率。欧氏距离不是一种精确可靠的判别方法[14]。例如,考虑如图1所示的使用链。 图1 Markov模型使用链 现假设两个不同的测试链A、B有很大的差异,是由两组独立的测试实验产生的。在测试链A中,状态Start的两条迁移边的转移概率与使用链中的对应边的转移概率相同,而图1云结构中包含使用链大量其它状态和迁移边的转移概率与测试链A中的相应状态存在较大差异。 在图2所示的测试链B中,情况则恰恰相反。状态Start的两条迁移边的转移概率与使用链中的对应边的转移概率差异较大,而测试链B云结构中包含测试链A的大量其它状态和迁移边的转移概率与使用链中的相应状态大致相同。 图2 Markov模型测试链B 当通过上述情况计算欧氏距离时,由于测试链B与测试链A相比较有更多的边转移概率和使用链相近,因此欧氏距离将表明创建测试链B的测试将被解释为比测试链A所代表的测试经验更能代表软件的预期使用,而实际上测试链A更接近于使用链。如果以这种方式解释欧氏距离,那么在软件测试过程中就有可能浪费时间来修复云结构中发现的相对不重要的故障,而且有可能错过通过测试从Start到状态A的过渡而暴露出的重要故障。因此,欧氏距离可能产生误导性解释,导致软件测试充分性的误判。 综上,欧氏距离在度量使用链和测试链的吻合性上存在较大偏差,且存在欠充分误判为已充分的风险。 Kullback判别式表示两个随机过程的对数似然率的期望值[15],它可以对使用链和测试链之间的相似性进行度量,该判别式的值则称为Discriminant值。其数学表达式如下 (8) 其中,在比较使用链和测试链的具体情况下,n表示测试用例的个数,X0,X1,…,Xn是使用链生成的长度为n的输入序列。由Markov链模型迁移边所对应的状态转移概率可知,上述公式等价于 (9) 从上式不难看出使用链和测试链的差异程度越小,K(U,T) 越趋近于0,测试也就越充分。当它小于某个特定的阈值时,即判定测试已经足够充分,便可停止测试。Discriminant值所提供的判定结果较为准确,但其结果并不总是可以被计算出来的[16]。当测试链中的所有状态和转移边仍未被未完全覆盖时,测试链产生的序列的概率接近于零,这就导致了判别式计算中的除数为零,即存在i,j, 使得ti,j为0时,Discriminant值便不可计算。因此可以用一种变体计算方法来避免上述情况,使其在任何情况下K(U,T) 都可以被定义[17] (10) 虽然基于Kullback判别式的测试充分性准则比基于欧氏距离的测试充分性准则有更高的准确度,但在一定程度上也存在测试充分性判定“早熟”的问题。考虑图3所示的Markov模型片段。 图3 Markov模型片段 通过上述分析可得,基于欧氏距离和Kullback判别式的软件测试充分性准则并未满足迁移对覆盖准则,而仅仅满足了测试充分性判别准则中的状态和迁移覆盖准则,这就意味着会出现“早熟”现象。因此,有必要对上述两种测试充分性判别准则进行改进,使其满足迁移对覆盖准则,来解决欧氏距离和Kullback判别式进行充分性判定过程中出现的“早熟”现象,同时在确保效率的前提下提高软件测试的充分性。 由于在一阶Markov链模型中的“无后效性”,使得任一状态只能被前一状态所影响,而间隔状态之间的相互影响则无法被涉及到。因此将单纯Markov链模型扩展为二阶,使得改进后的测试充分性准则尽可能地覆盖多个状态的所有可能组合。 由式(4)可得,状态Si经2步转移到状态Sj的状态转移概率即为P{X(n)=Sj|X(m)=Si}=pij(2), 称P(2)为Markov链模型的二阶转移概率矩阵,其矩阵表示如下 (11) 相对熵的概念来自于信息论和概率论,是由统计学家Kullback和Leibler提出的[18],因此又称为KL散度(Kullback-Leibler divergence)。其描述了两个不同概率分布间差异的非对称性度量。设状态空间为x∈X,p(x) 是Markov使用链的状态转移概率,q(x) 是测试链的状态转移概率,则最优编码平均长度的字符集的熵为 (12) 且拟合Markov测试链的平均编码长度为 (13) 由于Markov测试链和使用链存在一定的偏差,因此可以用相对熵来衡量使用链和测试链的相似程度,则其原始的相对熵的计算公式为 (14) 考虑Markov链中状态的平稳分布率πi,且Markov使用链的状态转移概率为uij,测试链的状态转移概率为tij,所以Markov链偏差计算公式为 (15) 其中,从Markov使用模型的任意状态Sk到状态Si的转移概率近似等于状态Si长期运行的发生概率,即状态Si的平稳分布率πi。 相对熵有如下两个主要的性质[19]: (1)不对称性:虽然KL散度从直观的角度来说满足距离度量函数的特性,但由于它不满足对称性,即KL(p‖q)≠KL(q‖p), 因此它并不能被称为真正的度量或者距离; (2)非负性:KL(p‖q)≥0, 当且仅当p(x)=q(x) 时等号成立,两个分布相差越大,相对熵越大。 由于KL(p‖q) 不满足对称性,即使用链和测试链的差异程度不能完全代表测试链和使用链之间的差异程度,因此KL(p‖q) 不适合作为测度,故对KL(p‖q) 进行对称性设计,使其变为一个完全的差异度量函数,其对称形式的相对熵公式如下 KLD(p‖q)=KL(p‖q)+KL(q‖p) (16) 当且仅当p(x)=q(x) 时,KLD(p‖q)=0,KLD指标具有无界性,可解释性不强[20],不适用于测试充分性评价测度。故提出一种基于对称形式的改进相对熵的测试充分性评价指标IKLD,其计算公式如下 (17) 基于改进后的相对熵具有如下性质: (1)对称性:IKLD(p‖q)=IKLD(q‖p); (2)有界性: 0≤IKLD(p‖q)≤1, 当且仅当p(x)=q(x) 时,IKLD(p‖q)=1。 并且IKLD(p‖q) 值是不增的,保证了测试充分性判别过程的收敛。因此当两个分布越接近时,测试充分性评价指标越接近1。反之,两个分布相差越大,指标越接近0。 因此最终的基于二阶Markov模型的改进相对熵测试充分性准则的公式如下 (18) 将基于二阶Markov模型的改进相对熵测试充分性评价指标IKLD′应用到实际软件测试中时,其软件测试充分性判别过程如图4所示。首先设定一个用于指示测试在何时停止的无限接近于1的阈值α,根据软件在真实场景中的使用方式,构建Markov使用模型并确定模型中各条迁移边上的状态转移概率。根据相应的测试指标来生成测试用例,最终形成一条完整的测试链并执行测试[21]。最后依据测试充分性准则所得出的结果来对测试执行过程的充分性进行评估: 图4 软件测试充分性判别流程 (1)当根据式(18)计算出来的IKLD′(p‖q) 值小于或等于α时,表明测试链和使用链相差较大,测试不充分,此时应继续生成测试用例并执行测试; (2)当IKLD′(p‖q) 值大于α时,表明测试链和使用链之间的差异性较小,测试已经足够充分,此时便可停止测试。 为了进一步验证基于二阶Markov模型的改进相对熵测试充分性准则的有效性,并且能够在一定程度上解决测试过程中出现的“早熟”现象等问题,本节通过数值模拟的方法进行对比实验来举例说明。 考虑图3的Markov模型片段作为该数值实验模型,在测试执行过程中分别通过欧氏距离、Kullback判别式和基于二阶Markov模型的改进相对熵3种判别方法进行测试充分性判定。其中,在计算Kullback判别式中的Discriminant值时,需设定一个趋近于0的正数作为式(10)中ε的取值,且ε越小,判别式的计算结果越精确。考虑到实际情况,当ε≪min(tij) 时,可以将ε对计算结果精度的影响忽略,因此令ε=0.000001(ε≪0.25)。 同时为了便于说明测试过程,将模型中迁移边a和b的状态转移概率分别设为1/2,其它迁移边均保持不变。其数值实验结果见表2。 表2 基于Markov模型的测试充分性判定 由于基于二阶Markov模型的改进相对熵判别方法的计算结果的有界性,为了使得上述实验数据具有一定的可比较性,故将IKLD(p‖q) 值改写为IKLD′(p‖q)=1-IKLD(p‖q), 并且对3种判别方法的计算结果进行归一化处理,处理后的数据映射在0~1范围之内,以消除不同评价指标之间的相互影响,从而便于对实验数据进行综合对比评价。处理后的数据见表3。 表3 基于Markov模型的测试充分性判定(归一化处理) 测试在初始状态时,测试链为空,欧氏距离的计算结果达到最大值。而对于所有状态,其平稳分布率πi都为0,此时经处理后的Kullback判别式和基于二阶Markov模型的改进相对熵的值均为0。当生成测试用例ACDFG、ABDEG后,即此时的测试链为(ACDFG、ABDEG),欧氏距离和Kullback判别式的计算结果为0,表示测试执行过程已充分,而相同条件下基于二阶Markov模型的改进相对熵的值表明测试仍未充分执行,应继续生成测试用例并执行测试,因此基于欧氏距离和Kullback判别式的充分性准则在此时出现了“早熟”现象。而当测试链为(ACDFG、ABDEG、ACDEG、ABDFG)时,3种充分性判别准则的计算结果都为0,此时则说明使用链和测试链已经完全重合,测试过程充分执行,即可停止生成测试用例。 从上表可以看出,欧氏距离和Kullback判别式在测试执行未充分时就显示计算结果为0,即在测试过程中出现了“早熟”问题,而基于二阶Markov模型的改进相对熵能够很好地度量使用链和测试链之间的差异程度,大大降低了出现“早熟”现象的概率。因此,基于二阶Markov模型的改进相对熵的测试充分性准则相较于传统的测试充分性准则有更好的有效性和稳定性。 本文对Markov链模型的基本概念和性质进行了介绍,并对现存的基于Markov模型的软件测试充分性判别准则作了系统性的分析,针对现有测试充分性判别准则存在的缺陷,给出了一种基于二阶Markov模型的改进相对熵测试充分性准则作为对测试终止的判断依据。该方法通过分析软件单元的状态迁移关系,进而确定软件单元测试的测试覆盖因素,使得单元测试过程得以模型化描述,其单元测试的充分程度能够得到定量的计算,对单元测试的测试用例生成策略的优化设计存在一定的指导意义。同时,该方法由于对测试充分性准则进行了边界化处理和对称性设计,并且消除了Markov模型的“一阶无后效性”的影响,因此有效解决了测试用例生成过程过早收敛即“早熟”问题,避免了测试充分性的误判。 但是基于模型的软件测试充分性准则只能用于评估当前测试经历匹配软件预期使用的程度,而近似相等概率则可以提供关于测试链未来行为的量化信息,因此基于模型的软件测试充分性准则和近似相等概率可以结合使用,一旦测试收敛,测试人员便可得到关于当前测试经验和软件预期使用的相似性的指示。后续工作中,将继续对以上问题开展深入研究。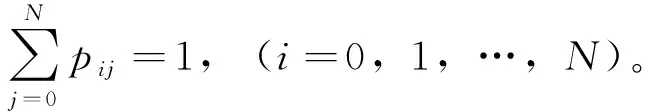
2 基于Markov模型的测试充分性准则
2.1 欧氏距离
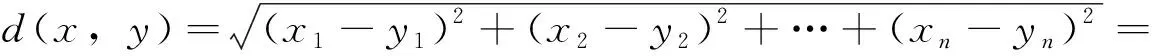

2.2 Kullback判别式
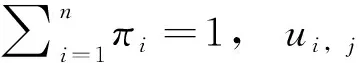

2.3 测试充分性判别方法的缺陷


3 基于二阶Markov模型的改进相对熵测试充分性准则
3.1 二阶Markov模型引入
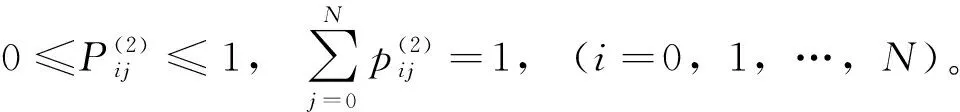
3.2 改进相对熵的定义
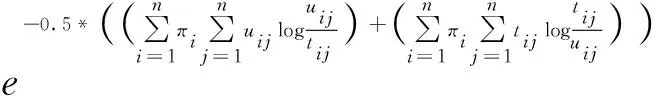

3.3 基于二阶Markov模型的改进相对熵充分性判别流程
4 数值实验
4.1 实验过程

4.2 实验结果分析
5 结束语

