组合钢架式网箱水动力性能分析

张 婧，孙立文，周 游，施兴华

(江苏科技大学，船舶与海洋工程学院，江苏 镇江 212028)

中国海岸线长度位居世界第四，海洋养殖资源充足。但受中国海域气候的影响以及养殖设施性能的约束，海上养殖业发展不够充分。提高网箱系统抵御风浪流的能力以及研发新型养殖网箱变得尤为重要[1-4]。

国内外对于网箱系统已经进行了大量研究，黄六一等[5]、张本[6]通过对张力腿网箱进行水动力特性试验以及实地考察发现，张力腿网箱具有好的抗风浪性能。单恒年等[7]对重力式网箱进行了水动力分析，网箱的连接构件数量增加时，浮架应力和变形将会减少。董海国等[8]、隋留洋等[9]和陈昌平等[10]都对重力式网箱的锚绳力进行研究，结果表明波流同向下的锚绳力大于波流逆向，多点系泊时的系泊力峰值大于单点系泊。徐为兵等[11]和崔勇等[12]对蝶形网箱进行了多海况下的数值计算，证明了流速对锚绳张力影响最大，双层网底网箱的最大锚绳力均大于单层网底网箱。崔江浩[13]、江涛等[14]对网箱进行耐流特性研究，不同流速下数值模拟与试验结果相差不大。熊占山等[15]研制出了淡水组合式浮动网箱。刘永利等[16]通过对网箱在横，纵两种排布下的模型试验，验证了在流速高时，纵向排布方式抗风浪性能最好。郭根喜等[17]对高密度聚乙烯圆形网箱锚绳受力实测试验，验证了锚绳受力与流速呈正比关系。赵国正[18]对单体、双体和四体方形网箱进行了水动力分析，结果表明四体方形网箱运动幅度最小。Decew等[19]用试验和数值模拟的方法研究了一种重力网箱的水动力性能，结果表明锚绳力试验结果比数值模型大。Zhao等[20]通过对箱型和柱形网箱在纯波和纯流中进行仿真，结果表明柱形网箱比箱型网箱更稳定，养殖量更多。Hu等[21]采用ABAQUS研究了2×2组合式网箱系泊系统的运动响应，结果表明双系泊系统的系泊张力大于正交系泊系统。Xu等[22]通过一系列物理模型试验验证了网箱在水面以下时，网箱变形，网线拉力将明显降低。Myrli等[23]通过流固耦合的方法研究网笼的使用寿命，结果表明聚氨酯网线能够延长网笼使用寿命。

组合式网箱能够满足产业化和规模化的发展要求[24]，是海上养殖业未来的发展方向。目前，组合式网箱大多数都采用串联式和双列式[25]，外网箱包围内网箱这种形式的组合网箱在海上养殖中已经有所应用。在实际应用中，铰接外网箱后的组合钢架式网箱水动力性能会与铰接前钢架式网箱的水动力性能有很大差别。

本研究对组合钢架式网箱进行水动力性能分析，计算各连接系统的受力及网箱的容积剩余率，并与钢架式网箱的容积剩余率及连接系统受力进行对比，为在实际中运用铰接外网箱扩大养殖空间提供依据。

1 水动力学相关理论

1.1 集中质量法

由于网箱结构中的网线及锚绳都属于柔性杆件，在进行数值模拟中，采用集中质量法[26]进行计算，假定网衣结构由有限无质量弹簧连接的集中质量构成，集中质量点在网目的中间和两端，锚绳离散成多个集中质量点与构件。

根据牛顿第二定律，集中质量点的运动方程为：

(1)

式中：M为集中质量点的质量；a为集中质量点的加速度；F为集中质量点所受水流力；T为网线张力；B为浮力；W为重力。

1.2 Morison方程

一般在计算网衣与锚绳这类细长杆件水动力荷载时，会忽略自身结构对波浪的影响，本研究应用OrcaFlex中拓展后的Morison方程[27]的来计算水动力载荷，方程为：

(2)

式中：f为作用在物体上的单位流体力；Cm=1+C∂为惯性力系数；Δ为排水量；af为水质点绝对加速度；ab为物体绝对加速度；Cd为拖曳系数；vf为水质点绝对速度；S为拖曳面积。

1.3 网箱容积剩余率计算

网箱在纯流，纯波浪和波流工况下，在一段时间内的容积剩余率是不断变化的，最终会达到稳态，此时容积剩余率会处于恒定的状态。本研究计算容积剩余率采用Lader等[28-29]提出的方法。图1为该方法标记点示意图。如图1所示，在圆形网衣上进行标记并编号01、03、05、21、23、25、31、33、35。坐标系原点设置在顶部中心，X方向与水流方向相同，Z方向为水流方向的法向，XZ平面为网衣的对称平面。因为网箱是对称的，所以测量计算是仅考虑网箱一半。图中标记的位置用于计算网衣的体积减小量。

图1 标记点示意图

通过考虑编号为01-03-05-21-23-25和21-23-25-31-33-35的2个三棱柱的体积减去1/2中心岛体积，计算出圆形网衣体积减小的估计值。每个三棱柱的体积可以用Vp来表示：

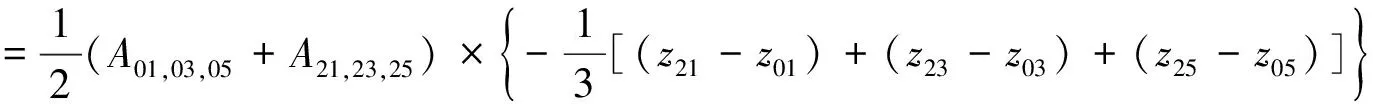
(3)

式中：An1,n3,n5为跟踪点n1、n3、n5所围成的三角形面积，Zn为n点的Z坐标值。容积剩余率Cur如下表示：

(4)

式中：VP0为三棱柱在初始时的体积；Vc为1/2中心岛的体积。

2 组合钢架式网箱模型及计算工况

2.1 组合钢架式网箱特点与参数

组合钢架式网箱主要由中心岛、浮架、网衣和锚碇系统等组成，中心岛与内网箱浮架间采用36块板连接，板长30 m，两板之间夹角10°。在内网箱与外网箱的浮架之间布置有36根铰链连接，设置约束条件，实现铰链上下运动。外网箱网衣网目与内网箱网目数一致。表1所示，为钢架式网箱和锚绳的具体特征参数。图2a、图2b分别为组合钢架式网箱的主视图和俯视图，图3a、图3b分别为钢架式网箱的主视图和俯视图。

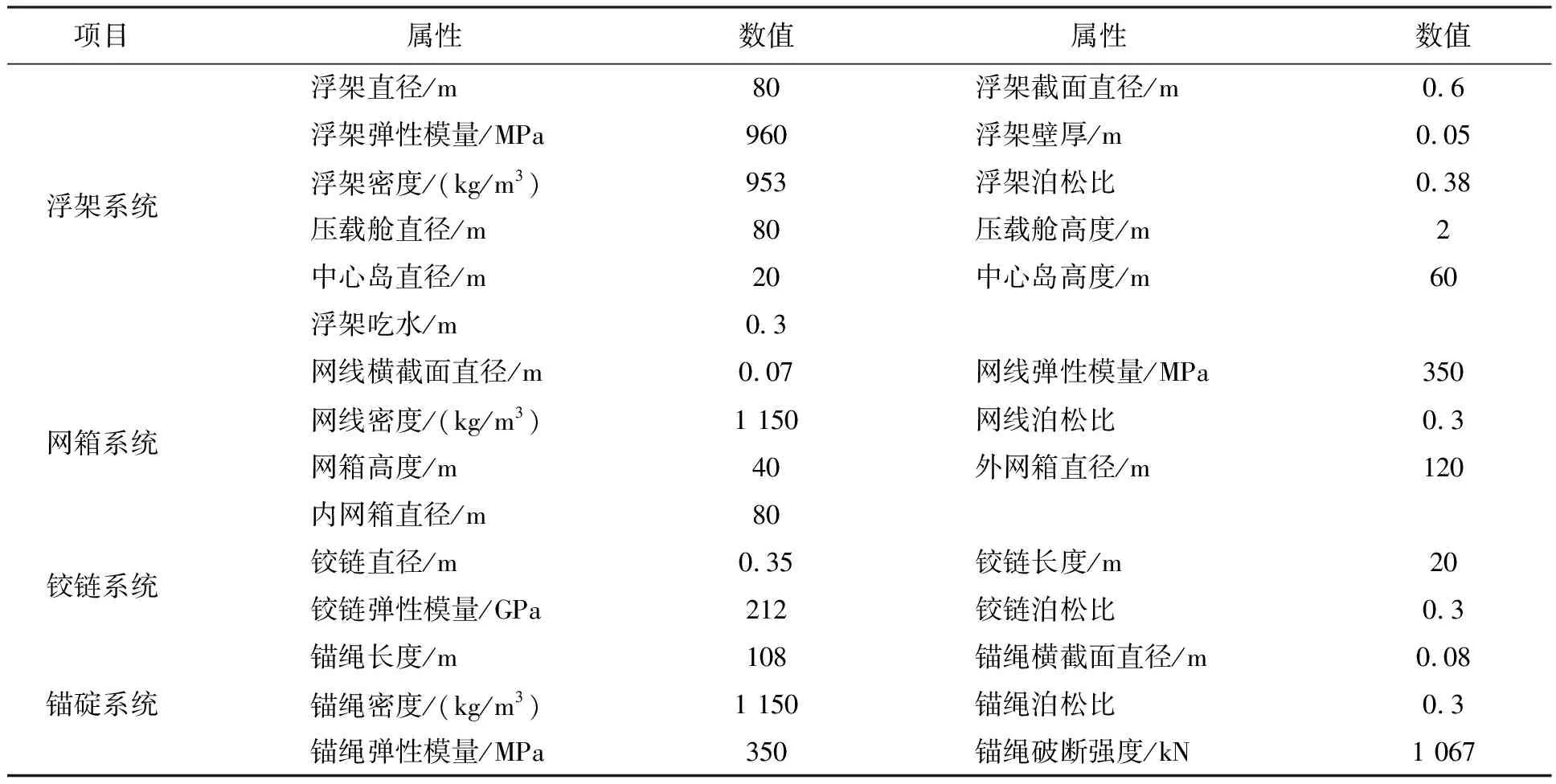
表1 网箱参数

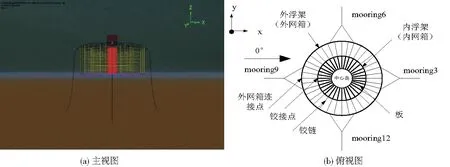
图2 组合钢架式网箱

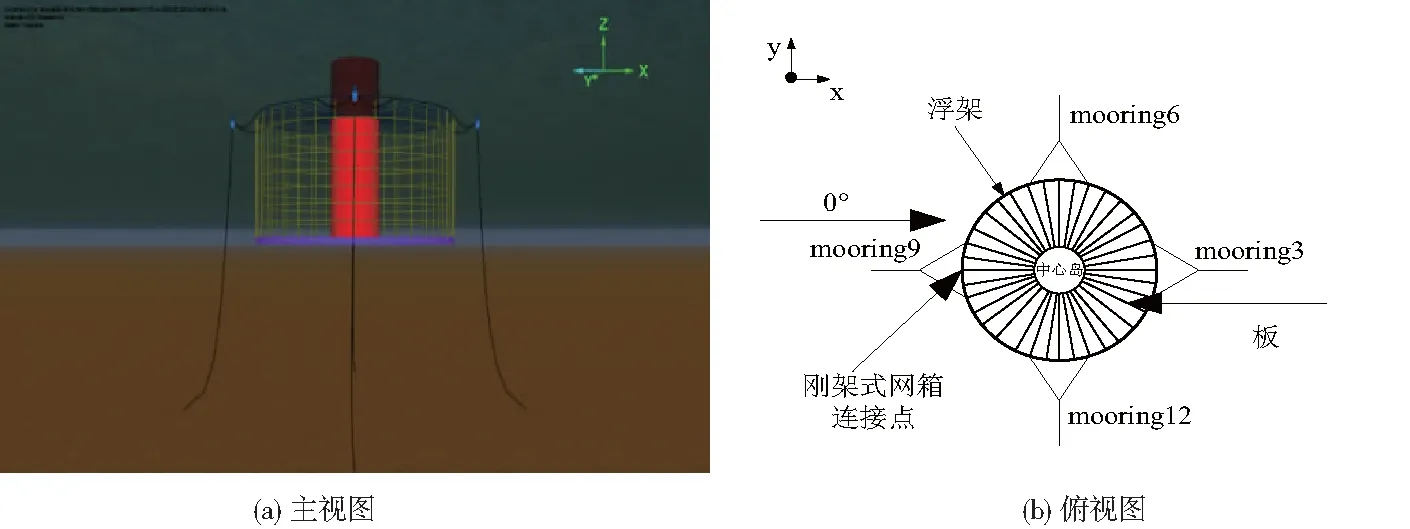
图3 钢架式网箱

2.2 网衣模型

网衣数值模型是利用水动力有限元分析软件Orcaflex建立的。在Orcaflex软件中，网衣模型由“line”模型和“3Dbouy”模型组合而成[30]。“line”模型被用来建立网线，通过设置不同的材料参数给予模型不同的特性。“3Dbouy”模型为三自由度的小浮体，体积很小，可以布置成小浮标或者连接网线的节点。图4为网衣的数值模型，图4中01-02表示一段网线。

图4 网衣数值模型

2.3 计算工况

本网箱布置在福建海域，结合实际海域，考虑在纯流，纯波流及波流联合3种工况下对连接内外网箱的铰链进行运动响应分析，对组合钢架式网箱和钢架式网箱的浮架与网衣连接点张力，网箱容积率和锚绳力进行水动力对比分析，具体工况如下：

纯流工况下，入射水流为0°，流速分别为U=0.25 m/s、1 m/s、2.25 m/s、4 m/s，水深为100 m；纯波浪工况下，波高为H=1.3 m，周期T=6、7、8 s及浪向0°，水深为100 m；波流工况下，流速U=4 m/s，波高H=1.3 m，T=6 s及波流夹角分别为0°、90°、180°，水深为100 m。

3 水动力分析

3.1 铰链系统垂向运动响应

铰链系统垂向运动响应是衡量组合钢架式网箱安全的重要参数。以铰接点初始位置为坐标原点，对铰接系统垂向运动响应进行分析。在实际海域中，波流是同时存在的，波流联合工况下铰链系统的垂向位移也更贴合实际。图5为网箱在不同波流夹角下铰链的垂向位移曲线。表2、3、4为铰接点和外网箱连接点在纯水流，纯波浪及波流联合作用下最大垂向运动幅度及最大有效张力对比。

图5 波流联合作用下连接点垂向位移

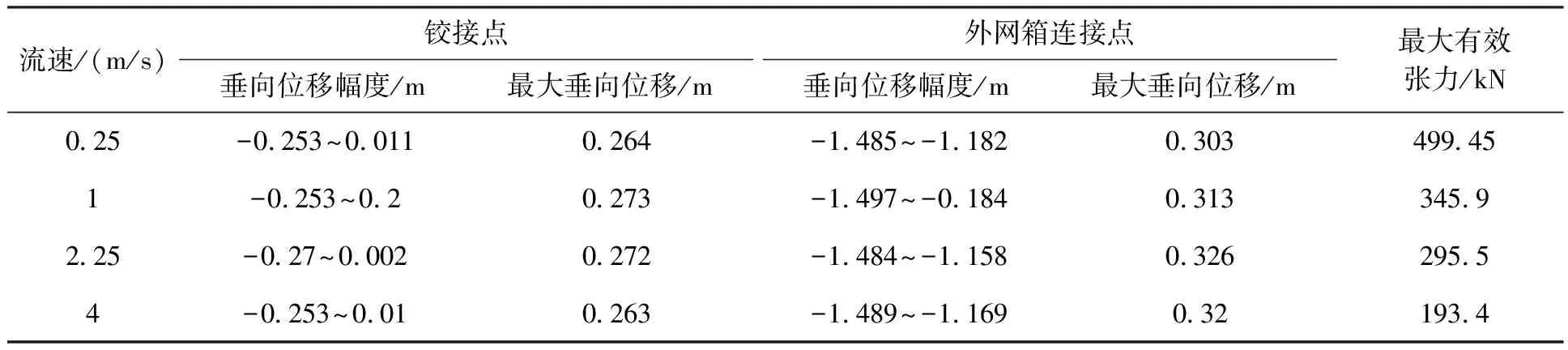
表2 纯流作用下铰链垂向位移及最大有效张力对比

表3 纯波浪作用下铰链垂向位移及最大有效张力对比

表4 波流联合作用下铰链垂向位移及最大有效张力对比

由图5可见，不同波流夹角下，铰接点的最大垂向运动幅度都小于外网箱连接点的运动幅度，在波流夹角为90°时，垂向运动幅度最大。由表2、3、4可见，在纯水流，波流联合工况下，铰接点的最大垂向位移幅度在不同流速，不同波浪夹角下数值结果相差并不大。但铰链的最大有效张力随流速的增加反而会减小，随波流夹角变大而增大。在纯波浪工况下，其最大垂向位移幅度随波浪周期增加而增大，铰链最大有效张力出现在周期T=7 s时。通过对比3种工况下的铰接点及外网箱连接点的最大垂向位移，可以明显看出纯波浪及波流联合工况下的最大垂向位移大于纯流工况，这说明铰链的垂向运动位移受波浪的影响较大。结合3种工况下铰链的最大有效张力数值，可以看出波流工况下铰链的安全性高于其他两种工况，也体现了通过铰链连接内外网箱这方案的可行性。

3.2 浮架与网衣连接点受力分析

选取与迎流面锚绳mooring 9最近的迎流面外网衣与外浮架的连接点，同时选取与迎流面锚绳mooring 9最近的迎流面内网衣与内浮架的连接点进行分析。图6为内、外浮架与网衣连接点在纯流，纯波浪及波流联合工况下的有效张力。

图6 连接点有效张力

由图6可见，3种工况下，外浮架与网衣连接点的有效张力始终比内浮架与网衣连接点和钢架式网箱连接点的有效张力大。由图6a可见，在纯流工况下，随着流速变大，连接点有效张力也变大。内外浮架与网衣连接点的有效张力差也变大。相比钢架式网箱的连接点有效张力，组合钢架式网箱的连接点有效张力始终大于钢架式网箱的连接点有效张力。由图6b可见，在纯波浪工况，外浮架与网衣连接点的有效张力和内浮架与网衣连接点的有效张力低于其他两种工况，这说明连接点有效张力受波浪的影响小于流以及波流联合的影响。由图6c可见，在波流联合工况下，外浮架与网衣连接点的有效张力和内浮架与网衣连接点的有效张力最小时出现在波流夹角为90°时，波流同向与波流逆向时有效张力相差不大。

3.3 网箱容积剩余率

网箱的容积剩余率不仅可以反映网箱生存空间大小，也可以反映网衣的变形程度。计算容积剩余率采用Lader[28]提出的方法。

图7为纯流、纯波浪及波流联合作用下组合钢架式内外网箱和钢架式网箱的最大容积剩余率。由图7所示，3种工况下，组合钢架式内网箱和钢架式网箱的最大容积剩余率大于组合钢架式外网箱最大容积剩余率，且组合钢架式内网箱和钢架式网箱的最大容积剩余率相差不大，这说明在钢架式网箱铰接一外网箱不会影响内网箱的生存空间。外网箱的最大容积剩余率也能达到90%以上。在纯流工况下，随着流速变大，网箱的剩余容积率变小。纯波浪工况下组合钢架式外网箱最大容积剩余率低于纯流及波流联合工况下的最大容积剩余率，这说明网箱的最大容积剩余率受波浪的影响低于流的影响。波流同向和波流逆向时网箱最大容积剩余率大于波流夹角90°时。图8为纯流工况下不同流速的网衣变形。随着流速的增大，网衣的变形程度也越大。

图7 网箱容积剩余率对比

图8 网箱稳态图

3.4 锚绳力分析

锚绳最大张力是衡量组合钢架式网箱系泊系统安全性的重要的参数之一。以迎浪侧锚绳mooring 9的锚绳受力情况为对象进行分析。图9为组合钢架式锚绳及钢架式锚绳在纯流，纯波浪及波流联合作用下最大锚绳力对比。由图9所示，钢架式网箱的最大锚绳力小于组合钢架式最大锚绳力，这是由于铰接外网箱导致的。铰接一个外网箱后的组合钢架式网箱最大锚绳力出现在波流夹角为0°的工况，相较于钢架式网箱增大了16%，且能够达到API RP 2SK[31]规范规定的安全系数。由图9a知，同一流速下，两者之间锚绳力相差较小，且随着流速增大，两种形式的网箱最大锚绳力都在增加。同时，纯流及波流工况下两种形式网箱的最大锚绳力都远大于纯波浪工况下，这说明流速对锚绳的影响较大。由图9c知，波流联合作用下，组合钢架式网箱的锚绳力最大。

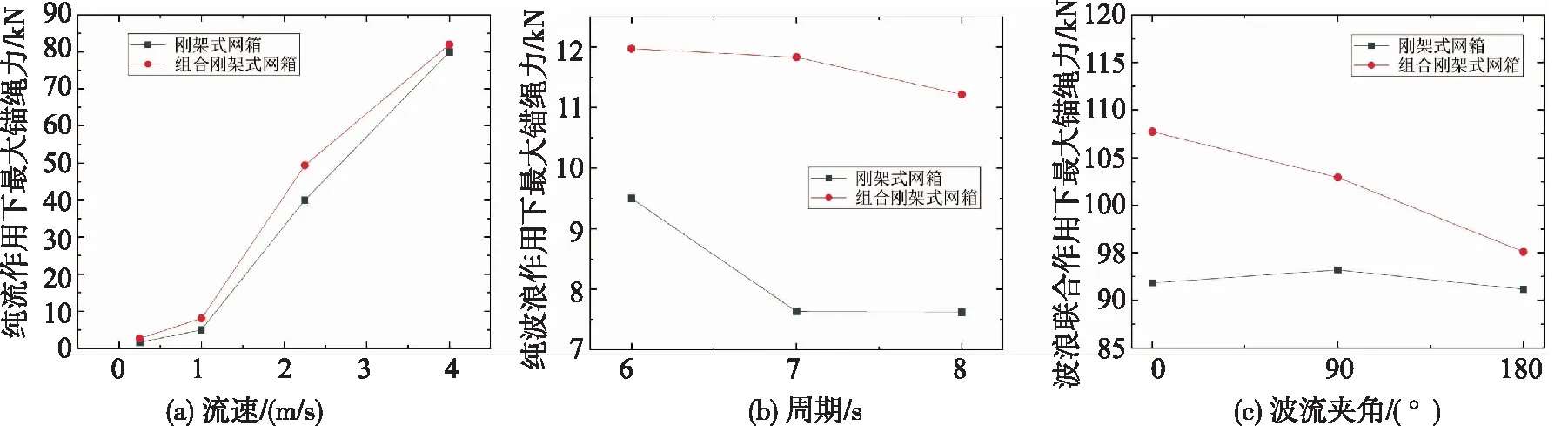
图9 最大锚绳力对比

4 结论

通过数值模拟对比分析组合钢架式网箱和钢架式网箱的水动力性能，结果显示，组合钢架式网箱的浮架与网衣连接点有效张力大于钢架式网箱连接点。因此，组合钢架式网箱浮架与网衣连接处需要保护措施，预防发生网衣断裂或浮架破坏。铰接点与外网箱连接点的最大垂向位移受流速的影响较小，铰链的最大有效张力会随着流速增加而减小，最大有效张力在波流联合作用下最小。组合钢架式内网箱在纯流、纯波浪和波流工况下的最大容积剩余率都在95%以上，外网箱的最大容积率能够达到90%，在纯流工况下内网箱最大容积剩余率高于钢架式网箱。这表明通过铰接外网箱在获得更大养殖空间的同时，对内网箱的养殖空间有一定保护作用。

□