耗散型随机非线性薛定谔方程的随机共形多辛方法

苗利军，陈红宇

(辽宁师范大学 数学学院, 辽宁 大连 116029)

对于随机偏微分方程，解析解的推导是十分困难.因此，数值方法成为研究方程解析解的有力工具.为了保证数值解长期模拟的可靠性和有效性，数值方法应尽可能地保持原始系统的固有性质.耗散型随机非线性薛定谔方程[1]是一类特殊的随机偏微分方程,具有随机共形多辛几何结构，在非线性光学和等离子体物理等领域都有重要应用.近几年，构造数值格式保持耗散型随机非线性薛定谔方程的几何结构越来越受到学者们的广泛关注，例如:Hong等人[1]研究了耗散型随机非线性薛定谔方程的随机共形多辛方法，文献[2]提出了乘性噪声驱动的随机非线性薛定谔方程的随机共形多辛守恒律，并构造数值格式保持该系统的随机共形多辛几何结构.受以上文章的启发，本论文将构造数值格式来保持加性噪声驱动的耗散型随机非线性薛定谔方程的随机共形多辛几何结构.

1 耗散型随机非线性薛定谔方程

考虑以下加性噪声驱动的耗散型随机非线性薛定谔方程[3]:

(1)

其中，λ=±1，耗散系数a>0，ε为噪声尺度，复值Wiener过程W(t)是定义在给定的赋σ-域流的概率空间(Ω,F,{Ft}t≥0,P)上的Q-Wiener 过程.

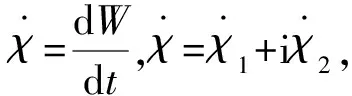
记v=px，w=qx，z=(p,q,v,w)T，上述方程可以转化为如下形式

Mdtz+K∂xzdt=-aMzdt+∇S0(z)dt+∇S1(z)°dW1+∇S2(z)°dW2，

(2)

其中，

以及“°”表示方程在Stratonovich型随机积分意义下成立.

定理1.1[1]方程(2)满足随机共形多辛守恒律

dtω(t,x)+∂xκ(t,x)dt=-aω(t,x)dt，

(3)

即

注1如果a=0，ε≠0，随机共形多辛守恒律(3)为随机多辛守恒律[4]:

dtω(t,x)+∂xκ(t,x)dt=0.

注2如果ε=0,a≠0，随机共形多辛守恒律(3)为共形多辛守恒律[5-6]:

dtω(t,x)+∂xκ(t,x)dt=-aω(t,x)dt.

注3对于方程(1)，当a=0,ε=0时，确定的非线性薛定谔方程满足多辛守恒律[7]:

命题1.1对任意a>0，下面的等式成立：

dt(eatω(t,x))+∂x(eatκ(t,x))dt=0.

证式(3)两边同时乘以eat有

eatdtω(t,x)+eat∂xκ(t,x)dt=-aeatω(t,x)dt，

则

[eatdtω(t,x)+aeatω(t,x)dt]+eat∂xκ(t,x)dt=0，

从而

dt(eatω(t,x))+∂x(eatκ(t,x))dt=0.

2 随机共形Euler box格式

引入微分算子

基于文献[6]，构造耗散型随机非线性薛定谔方程(1)的随机共形Euler box格式:

(4)

其中,

定理2.1随机共形Euler box格式(4)具有离散的随机共形多辛守恒律:

(5)

证将式(4)变形为

(6)

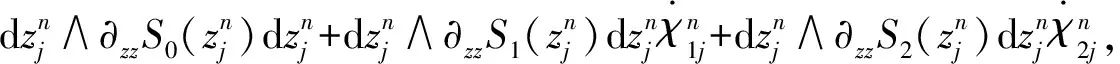
而上面等式左边的前两项

左边的后两项

因此，

(7)

故

命题2.2对任意a>0，下面的等式成立：

证式(7)的两端同乘eatn，得到

则

因此