再生框架结构的受力变形分析

杨 斌 周艳红

（中国水利水电第九工程局有限公司，贵州 贵阳 550081）

0 引言

再生混凝土框架结构具有经济、低碳和环保等优点，一直是研究的热点。当使用再生混凝土结构时，会受到冲击、地震和飓风等作用，这些不利因素会影响结构强度、引发工程事故，我国有大量区域处于地震频发区，研究地震作用下再生混凝土框架结构的屈服荷载与屈服变形变化尤为重要。

我国有许多学者对地震作用下的混凝土框架结构做了研究，周晓洁等[1]对混凝土砌块砌体填充墙结构进行了抗震性能研究，得到了不同连接方案的结构抗震性能。付国等[2]研究了地震作用下钢筋混凝土框架结构的延性破坏准则。徐其功等[3]研究了装配式混凝土结构的抗震性能，比较了梁柱节点构造对抗震性能的影响。于建东等[4]使用有限元软件研究了地震作用下型钢-混凝土结构的抗震性能。虽然目前对混凝土结构抗震性能影响的研究成果十分丰富，但是缺少对再生混凝土结构的抗震性能研究，再生混凝土取代率对抗震性能的影响规律尚不明确。该文使用有限元软件，依托贵州省黔南州中共贵定县委党校迁建项目，通过模拟再生混凝土框架结构分析了恢复力特征点，试验结果可以为再生混凝土框架结构的应用提供参考。

1 项目概况

该项目为贵州省黔南州中共贵定县委党校迁建项目，位于贵州省黔南自治州贵定县城关镇姜家庄，建筑面积为18771.66m2。

该项目含接待中心、人才公寓、会务中心、综合教学楼、学员宿舍、综合食堂和附属设施等，均为框架结构，抗震等级为二级，设计使用年限为50年，抗震设防类别为乙类，混凝土采用再生商品混凝土。依托项目现场制作结构模型，研究恢复力特征点。

2 结构模型

结构模型为再生混凝土框架结构振动台模型，模型总高4.5m、6层、两跨、两区间。结构模型采用基于刚度法的非线性梁柱纤维单元，忽略再生混凝土的抗拉，假定抗拉强度为0，钢筋选择三折线滞回材料模型。当对模型激励时选择汶川地震波（WCW-X）、上海人工地震波（SHW-X）以及El Centro地震波（ELW-X），确保能真实地反映结构在强震条件下的地震反应。为了研究骨料替代率、地震水平加速度和应变效率对结构的影响，设置4种替代率（0%、30%、70%、100%）、8种水平加速度（0.066g、0.130g、0.185g、0.370g、0.415g、0.550g、0.750g、1.170g）及4种应变速率（10-1s-1、10-2s-1、10-3s-1、10-5s-1）。

3 结构行为

3.1 恢复力特征

再生混凝土框架结构在非周期性地震作用下的恢复力可分为4个阶段，分别为弹性阶段、开裂至屈服阶段、屈服至最大荷载阶段和最大荷载至极限荷载阶段。如图1所示。

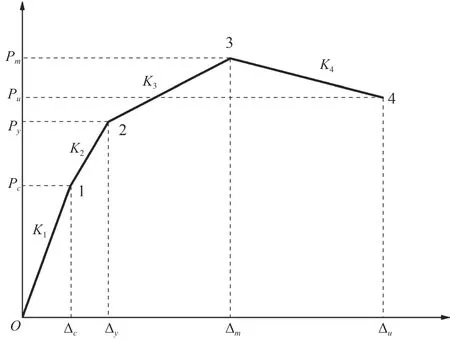
图1 恢复力模型

3.2 屈服荷载分析

图2为再生混凝土不同取代率对结构屈服荷载受应变率影响数据的回归分析，屈服荷载应变率影响因子的计算如公式（1）所示。

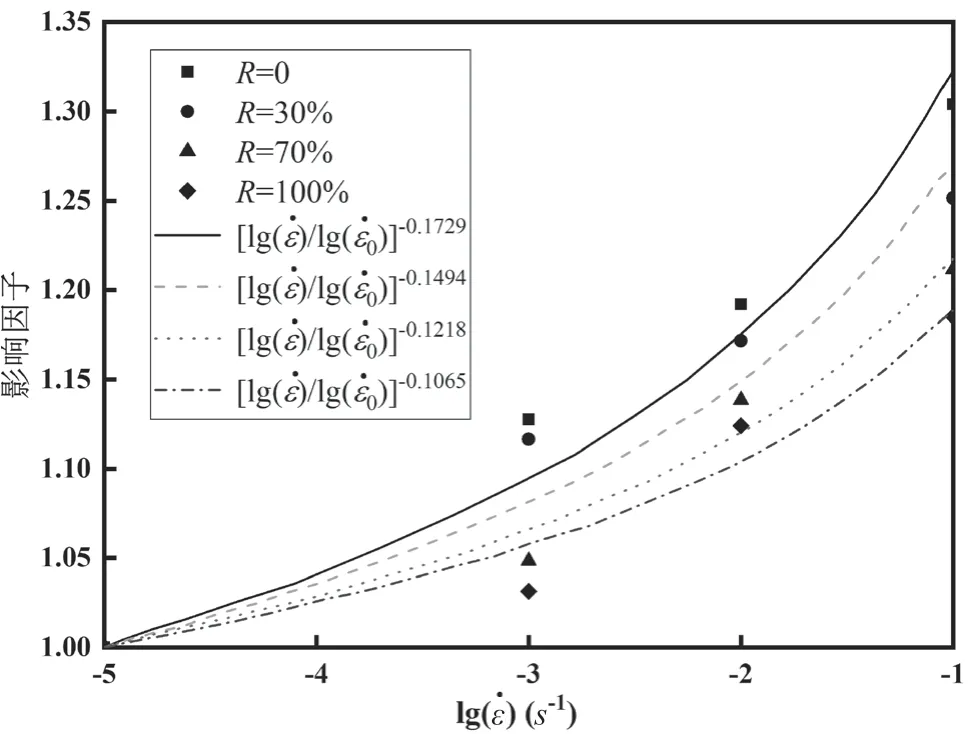
图2 屈服荷载应变率影响因子曲线

式中：kpy为屈服荷载应变率影响因子；ε为荷载应变率为准静态荷载作用下应变率；λi为屈服荷载应变率因子参数；i为1，2，3，4，取值见表1。

从图2中可以看出，当应变率增大时，影响因子随之增大。取代率对屈服荷载的应变率有较大影响，随着取代率的减少，结构的率敏感性逐渐增加，当取代率为100%时，屈服荷载率敏感性最大，当取代率为0%时，屈服荷载率敏感性最小[5-7]。由表1可知，随着取代率增大，λi逐渐增大，根据数据回归分析，得到取代率与模型参数关系表达式，如公式（2）所示。

表1 λi取值

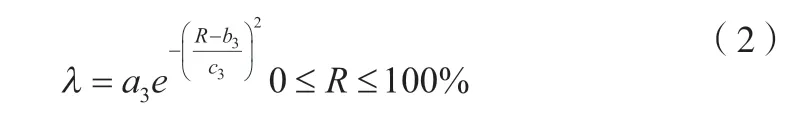
式中：a3为-0.6005；b3为-5.5780；c3为4.9890。

结合公式（1）与公式（2）可得到取代率与应变率对屈服荷载以及屈服荷载影响因子的影响规律，如公式（3）所示。

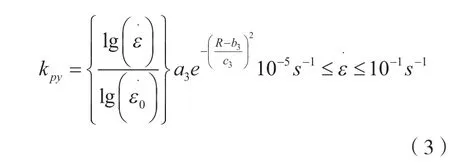
通过公式（3）得到屈服荷载归一化应变率影响因子，见表2。从表2中可以看出，当应变率逐渐增加时，屈服荷载应变率影响因子随之变大，当应变率为10-1s-1时的影响因子比当应变率为10-5s-1时的影响因子增加了32.1%（当取代率为0时）。在取代率不同的条件下，应变率对屈服荷载的影响规律如图3所示，由图可知，随着取代率增大，屈服荷载的率敏感性逐渐降低，当取代率为100%时的影响因子比当取代率为0%时的影响因子减少10.1%，表明与普通混凝土结构相比，再生混凝土结构在屈服极限状态下的承载力受应变率的影响更低 。

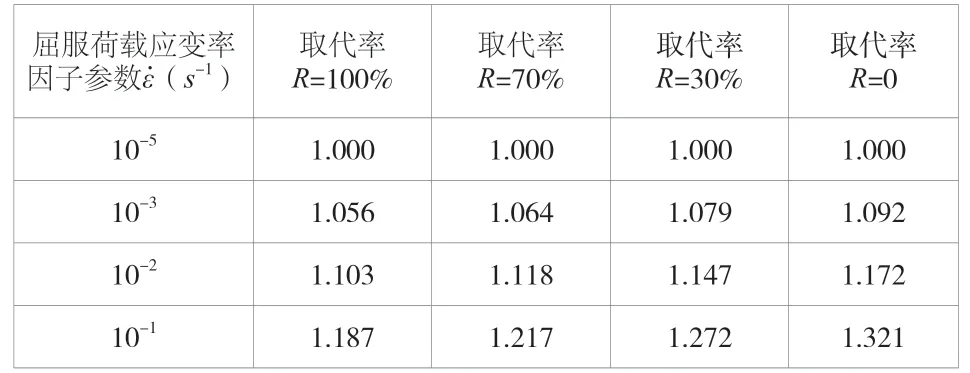
表2 归一化处理屈服荷载应变率影响因子

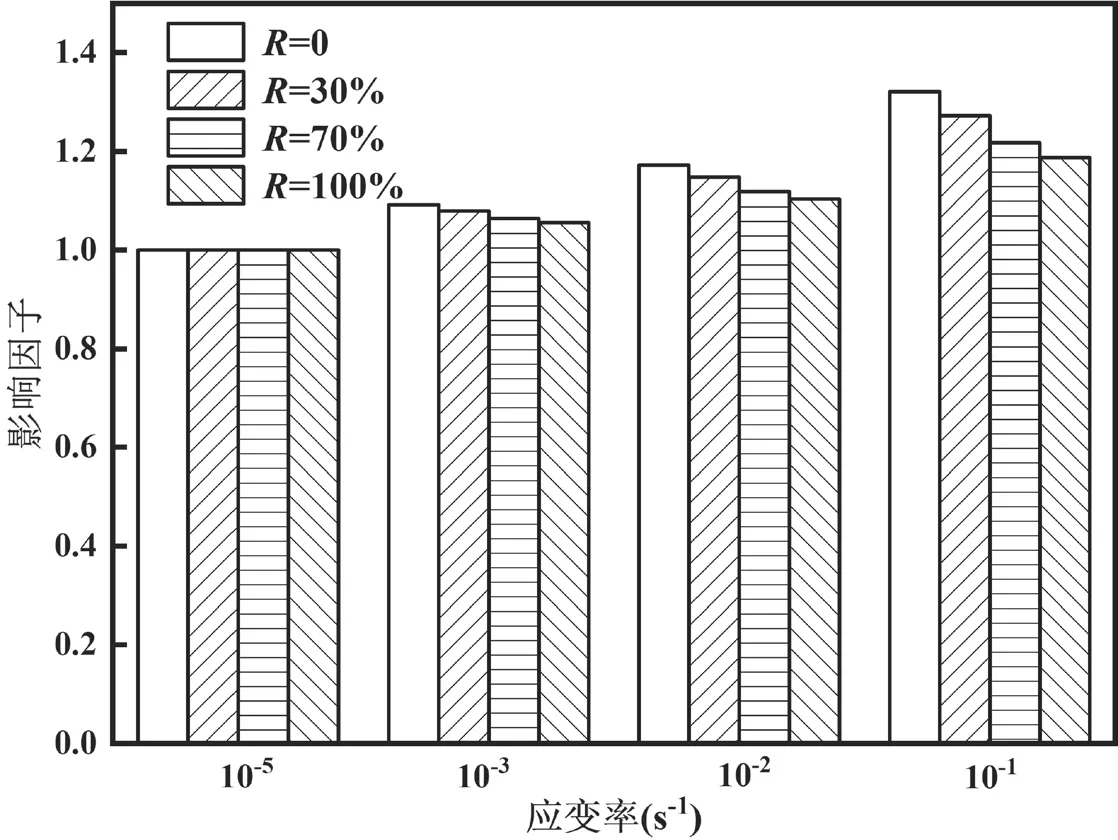
图3 不同R下屈服荷载应变率影响因子

3.3 屈服变形分析

屈服变形的应变率影响因子曲线如图4所示，其表达式如公式（4）所示。

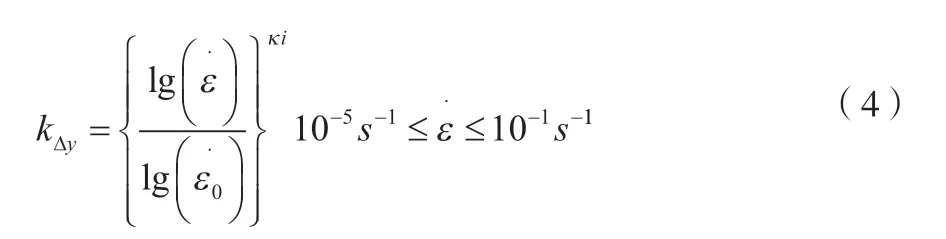
式中：k∆y为屈服变形的应变率影响因子；ε为荷载应变率；为准静态荷载作用下的应变率；κi是屈服变形应变率影响因子（i=1，2，3，4），取值见表3。

由图4可知当应变率逐渐增加时，结构屈服变形影响因子随之变大，取代率对屈服变形的应变率有较大的影响，随着取代率的减少，结构的率敏感性逐渐增加，当取代率为100%时，屈服变形率敏感性最大，当取代率为0%时，屈服变形率敏感性最小。根据表3中的数据可知，当取代率逐渐增大时，κ逐渐增大，根据数据回归分析得到取代率与模型参数关系的表达式，如公式（5）所示。

表3 ki取值

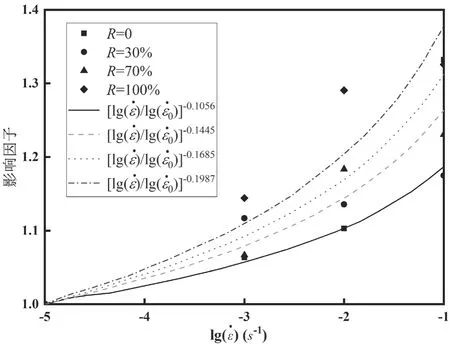
图4 屈服变形应变率影响因子曲线

式中：a4为-0.2178；b4为1.625；c4为1.955。

结合公式（4）与公式（5）可得到取代率与应变率对屈服变形以及屈服变形影响因子的影响规律，如公式（6）所示。

通过公式（6）得到屈服变形归一化应变率影响因子，见表4。从表4中可以看出，当应变率逐渐增加时，屈服变形应变率影响因子随之增大，当应变率为10-1s-1时的影响因子比当应变率为10-5s-1时的影响因子增加了32.1%（当取代率为100%时）。在取代率不同的条件下，应变率对屈服变形的影响规律如图5所示，从图中可知当取代率增大时，屈服变形的率敏感性逐渐变大，当取代率为100%时的影响因子比当取代率为0%时的影响因子增大16.2%，表明与普通混凝土结构相比，再生混凝土结构在屈服极限状态下的结构变形受应变率的影响更大，与屈服荷载率敏感性影响规律相反。

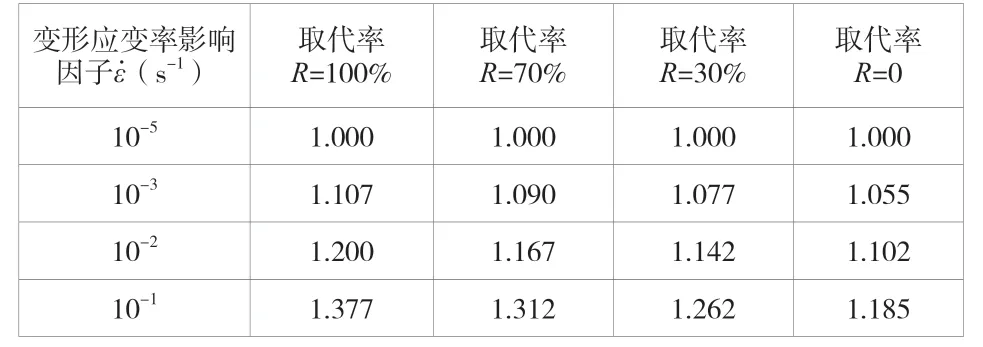
表4 归一化处理屈服变形应变率影响因子

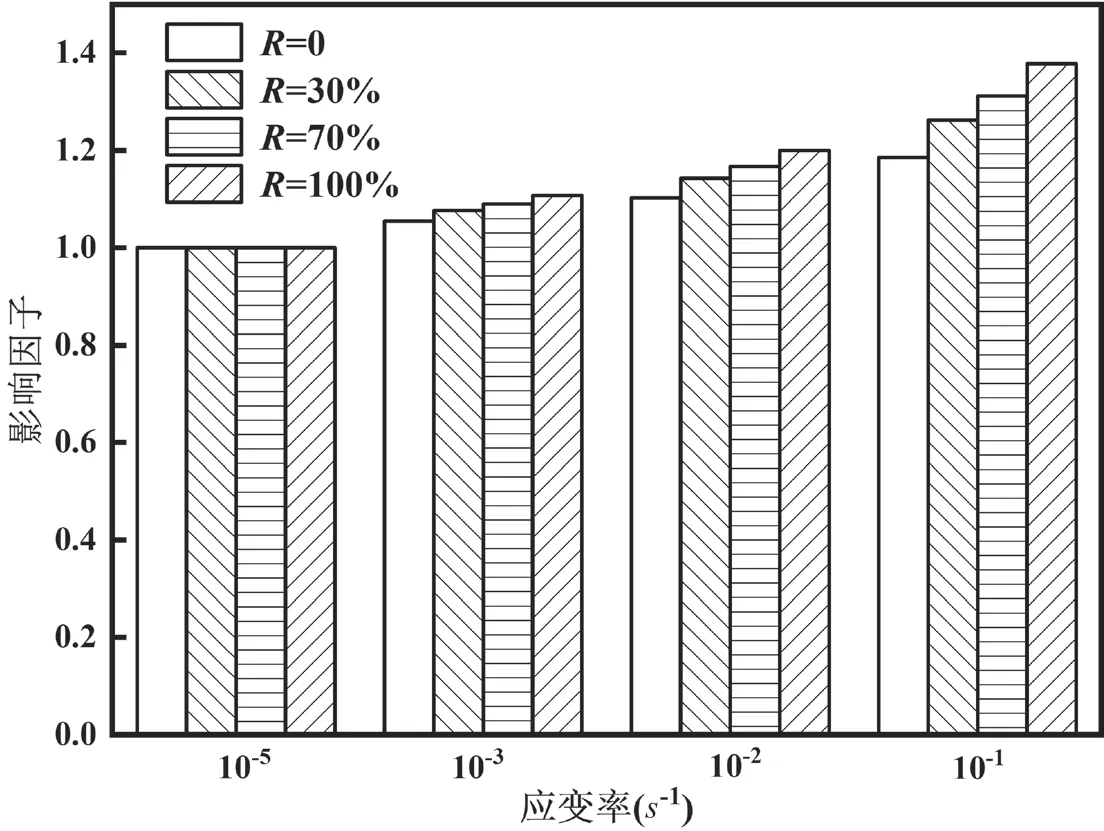
图5 不同R下屈服变形应变率影响因子

4 结论

该文使用有限元软件，依托贵州省黔南州中共贵定县委党校迁建项目，模拟再生混凝土框架结构并分析了恢复力特征点，得到结论如下：1）当应变率逐渐增加时，屈服荷载应变率影响因子随之变大，当应变率为10-1s-1时的影响因子比当应变率为10-5s-1时的影响因子增加了32.1%（当取代率为0时）。随着取代率增大，屈服荷载的率敏感性逐渐降低，当取代率为100%时的影响因子比当取代率为0%时的影响因子减少10.1%，表明与普通混凝土结构相比，再生混凝土结构在屈服极限状态下的承载力受应变率的影响更低；2）当应变率逐渐增加时，屈服变形应变率影响因子随之增大，当应变率为10-1s-1时的影响因子比当应变率为10-5s-1时的影响因子增加了32.1%（当取代率为100%时）。在取代率不同的条件下，当取代率增大时，屈服变形的率敏感性逐渐变大，当取代率为100%时的影响因子比当取代率为0%时的影响因子增大16.2%，表明与普通混凝土结构相比，再生混凝土结构在屈服极限状态下的结构变形受应变率的影响更大，与屈服荷载率敏感性影响规律相反。