基于DK算法的石化企业灭火救援路径优化技术

张建军

（青岛消防救援支队，山东 青岛 266000）

石化企业发生火灾将会危及人民生命和财产安全，必须进行及时有效的救援。从实际情况看，石化企业的火灾成因复杂、燃烧物质种类繁多并伴有爆炸等其他危险，导致救援工作困难[1]。同时，石化企业厂区内道路网络的复杂性，也进一步增加了救援难度。因此，要完成石化企业火灾的救援工作，首先要制定合理的救援路线，确保救援队伍和救援设备能够安全可靠、快速及时地到达救援现场[2]。在火灾现场中，救援路线可能由多个方案组成，哪一个方案更合理就需要通过路径优化技术来搜寻[3]。该文针对石化企业的救援问题特点，建立一种基于DK算法的救援路线优化方法。

1 基于DK算法的路径规划

石化企业的火灾救援路线的最佳选择，最重要的指标之一就是可以使救援总路径最短，从而提升救援效率。而DK算法就是一种最有针对性的最短路径搜索算法。DK算法的基本原理是，按照决策树的理论构建搜索救援的路径树，路径树的根节点应该满足到达其他节点的路径之和最短。

DK算法的具体实现过程如下：构建一个节点集合，并用S表示这个集合。在DK算法的初始状态下，S中就有一个节点，这个节点用v0表示。随着DK算法的搜索过程展开，不断会有新的路径搜索结果产生。设一条路径可以用其经历的节点集合为（v0，…，vk），那么就可以将vk添加到集合S中。按照这样的办法搜索到所有路径之后，全部节点都会纳入集合S中。

对找到的每条路径的长度，可以用下面的方法表示第k条最短路径，如公式（1）所示。

式中：参数dk为最短路径的长度，函数min{}为求取集合中所有元素的最小值，参数di为所有可能路径的长度，参数vi为节点集合中第i个节点，它可以是集合S中除去v0以外的任意一个节点。

随着搜索深度的增加，原有路径会有新的节点加入，使路径长度进一步延伸。当一个新的路径终点vk进入节点集合S以后，那么任意一条原有路径di应该按照下面的方式进行长度上的更新处理，如公式（2）所示。

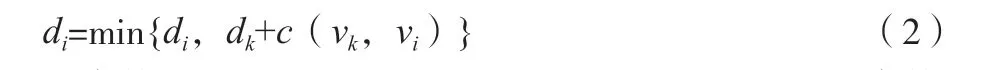
式中：参数（vk，vi）为节点vk到节点vi的弧的长度，参数c（vk，vi）则为节点vk到节点vi的弧上的权重大小。

根据有向图理论的最小权重值路径搜索策略如下。

第一，对最短路径长度的上界进行处石化处理，如公式（3）～公式（5）所示。

式中：参数d（v）为已经搜索到的全部路径的最短长度的上界，参数k（v）是设定的一个BOOL型变量，只有真（True）和假(false)两种取值，参数p（v）为一个定点的向后方向上的指针。

第二，不但执行对k（v）= 的扫描处理，计算其中的节点，是否会出现一个能够计算出新的最小长度的节点，如果可以得到，将其记录下来d（v）。

第三，与第二步相同的操作在相邻节点w上执行，即对k（w）=flase扫描处理，计算其中的节点，是否会出现一个能够计算出新的最小长度的节点，如果可以得到，将其记录下来d（w）。如果d（w）满足如公式（6）所示的条件。

则更新d（w）和p（w）。

第四，不断执行第二步和第三步，当k（v）=true是搜索过程结束，此时找到的路径即为优化后的最短路径。

2 DK算法的改进策略

2.1 DK算法的局限性

DK 算法的局限性有以下2点：第一，最短路径一般是基于单一条件限制下的最短，这时DK算法是有效的。但是，很多情况下最短路径的限制条件，同时包括多个指标，包括距离、时间、费用等。石化企业的救援工作中，这种路径的最短判定就包括更多因素。第二，DK算法的灵活性稍差，对一些突发情况难以应对。而石化企业的火灾救援，却经常会出现突发情况。

2.2 DK算法的改进

为了解决DK算法的局限性问题，也为了更好地解决石化企业的火灾救援问题，该文在DK算法的常规执行框架下，提出两点改进策略。

第一，同时进行正向和反向搜索，其策略如图1和图2所示。

图1 DK算法的正向搜索策略

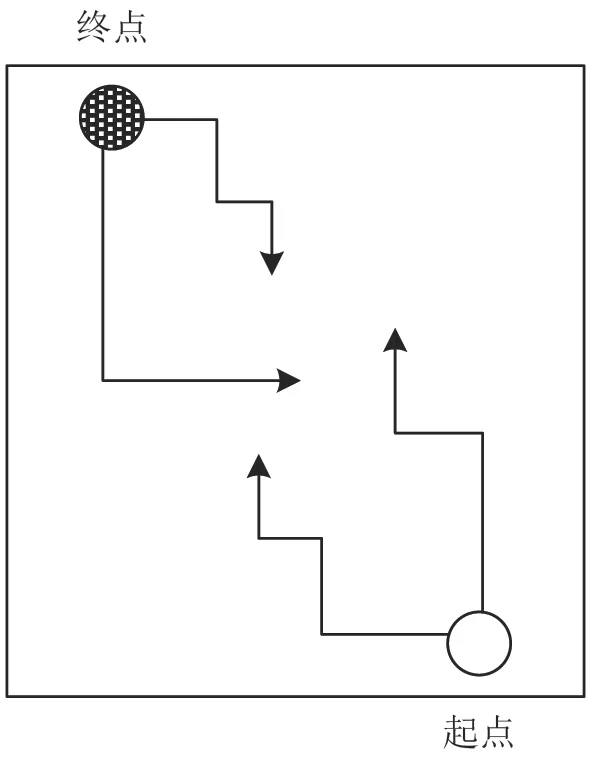
图2 同时进行正向和反向搜索的改进策略

图1和图2中，方框区域代表了石化企业火灾现场救援区域，白色圆点代表了救援路径搜索的起点，黑色圆点代表了救援路径搜索的终点，黑色实线代表了搜索路径和可能的搜索方向。

对DK算法而言，最优路径的常规搜索策略，就是从起点开始，按照DK算法的搜索规则，一边寻找可能的路径一边比较，直至找到一条到达终点的最短的路径。这种情况如图1所示。为了提高搜索效率并更好地满足多车辆协调救援任务的全局性要求，该文提出同时进行正向和反向搜索的改进策略，如图2所示。从图2可以看出，在DK算法的既定搜索规则下，最优路径同时从起点和终点开始进行搜索。从起点开始的搜索目标点是终点，这一搜索是正向搜索。从终点开始的搜索目标点是起点，这一搜索是反向搜索。同时进行正反向搜索，不仅提高了搜索效率，也可以在最优路径之后提供更多的次优路径被选，在多车辆集体救援时，可以根据优先级将最优路径、次优路径分别配置给各个车辆。

第二，对大场景的复杂区域，执行分区域搜索，其策略如图3所示。

图3中，外部的矩形框表示了整个的大场景复杂区域，其内部又被分割成4个小的区域，每个区域都有一些白色的圆点，这些圆点代表了分区域内的关键点，即救援路径必须经过的点。因为救援区域的场景大并且内部情况复杂，直接从起点到终点或者直接从终点到起点的路径搜索都会比较困难。为此，提出的分区域搜索策略，是将原始区域进行区域分割，形成一个个更小的区域。在每个小区域内，根据关键点必须经过的原则，在关键点之间执行路径搜索。在每个小区域内的局部路径确定后，再使各个区域之间的路径连接，从而形成完整的最优救援路径。

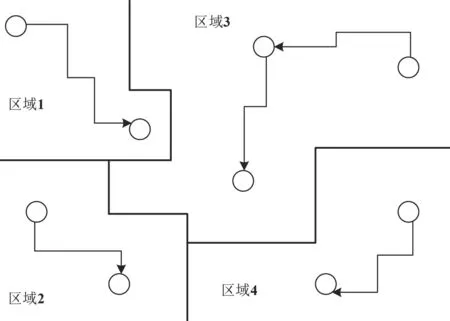
图3 大场景复杂区域的分区域搜索策略

通过以上两种改进措施，可以有效地解决DK算法的局限性，提升其灵活性、改善其全局最优的搜索性能。

3 石化企业火灾救援路径优化仿真试验

为了验证该文方法对石化企业火灾救援的有效性，接下来以仿真试验的形式对DK算法的救援路径优化性能进行验证性试验。

试验过程中，仿真试验所有的计算机配置情况如下：计算机的CPU为双核多线程处理器，单核主频为3.0GHz，计算机的内存大小为16GB，计算机的硬盘大小为500GB。仿真试验所使用的软件环境为MapX平台，这一平台专门为路径优化算法的验证试验提供试验环境。

首先，执行该文改进的DK算法，在石化企业复杂场景的模拟火情场地下进行救援路径搜索试验，分别得到最优救援路径和两个次优救援路径，救援路径规划的试验结果如图4所示。

在图4中，石化企业的整个火灾火场模拟区域设定为400个栅格大小，x方向上配置了20个栅格长度，y方向上配置了20个栅格长度。在这个400个栅格大小的火场区域上，救援车辆的起点位于x方向上位置为1、y方向上位置为20的栅格处，救援车辆的终点位于x方向上位置为18、y方向上位置为1的栅格处。从视觉效果上，救援车辆的起点位于场景中的左上方，终点位于右下方。同时，火场区域内有多个形状各异的障碍物干扰，障碍物所在位置设定为背景为叉剖面线的栅格区域，这些模拟障碍物在实际中可能对应着石化企业的厂房、储罐、原材料堆放区域等。

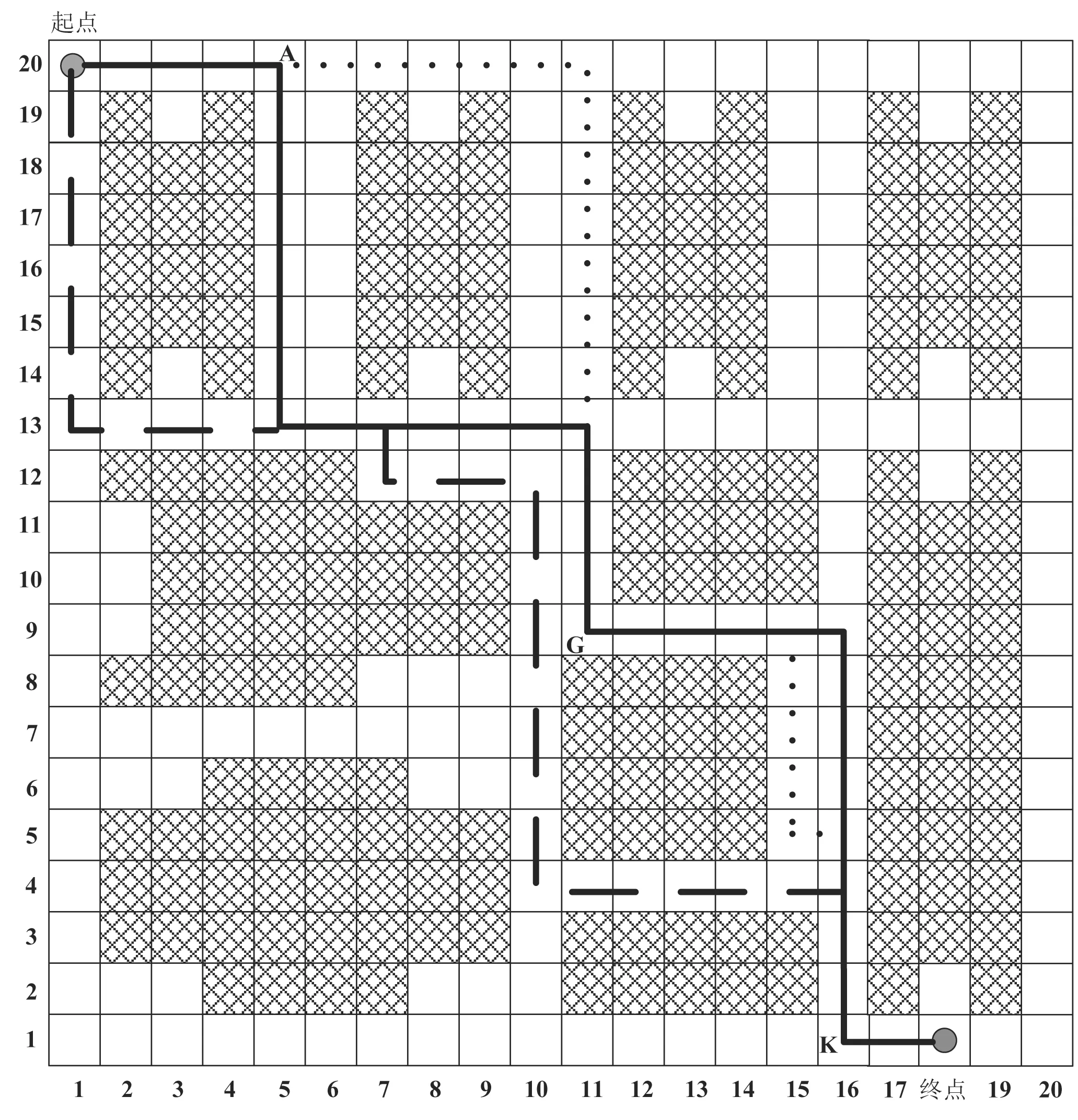
图4 应用该文提出的改进DK算法进行的石化企业火灾救援路径规划仿真试验结果

图4中，DK算法一共搜索到1条最优路径，如图中的黑色粗实线所示。同时，DK算法还搜索到2条次优路径，如图中的黑色粗虚线和黑色粗点线所示。三条路径都存在相互的重叠区域，全部以黑色粗实线覆盖。从DK算法的规划结果可以看出，最优次优路径都有效地避开了障碍物，并从起点顺利到达目标终点。

为了将该文采用的改进DK算法与传统 DK 算法进行对比，将另一组试验结果展示为表格形式，见表1。

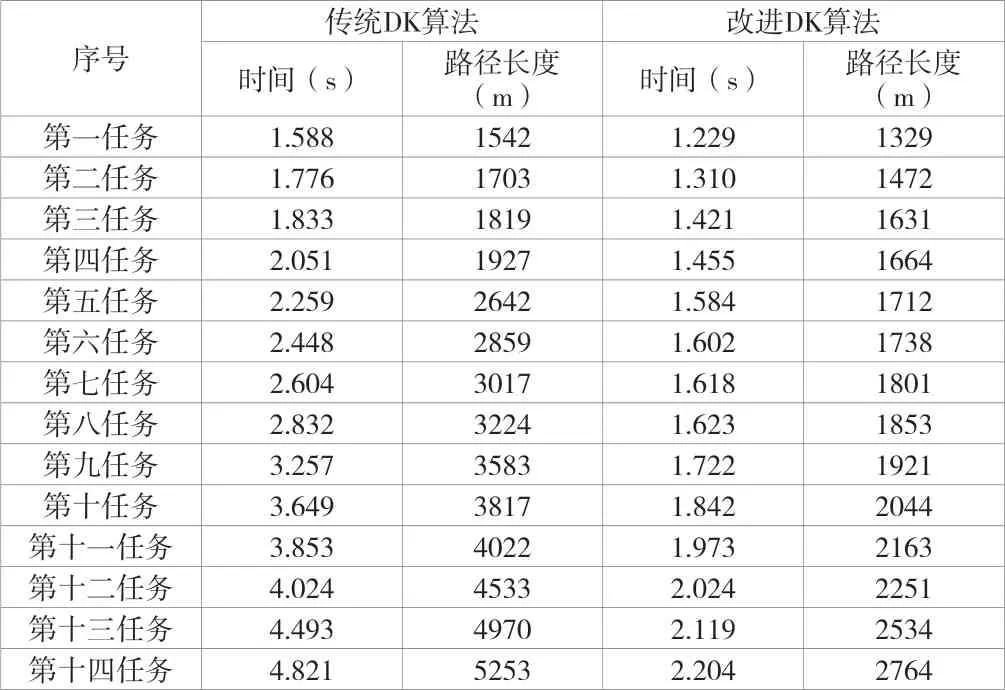
表1 该文改进DK算法和传统DK算法的性能对比

表1中分别说明了石化企业14组火灾救援的模拟任务，对传统DK算法和改进DK算法分别比较了路径规划时间和规划出的路径长度。从两项参数的对比结果可以明显看出，该文提出的改进DK算法，完成路径规划的时间更少，并且规划的最优路径更短。该结果说明了该文提出的改进DK算法对火灾救援的有效性，可以应用于石化企业的火灾救援工作。

4 结论

该文针对石化企业火灾救援难度大的问题，提出一种基于改进DK算法的救援路径规划方法。首先，介绍了传统DK算法的实现原理和操作流程。其次，分析了传统DK算法的局限性，提出了正方向搜获和分区域搜索的改进策略，提升了DK算法的灵活性和全局寻优性能。最后，在Mapx仿真环境下，针对石化企业火灾救援场景进行模拟，并分别采用传统DK算法和改进DK算法进行最优路径规划的对比试验。试验结果表明：该文提出的改进DK算法得到的最优路径更短，完成路径规划的时间更少，适合石化企业的火灾救援。