超大规模MIMO中包含球面波特征的最优传输方法研究
蒲旭敏,邓志伟,李 琳,陈前斌,金 纯
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
大规模多输入多输出(multiple input multiple output, MIMO)技术可以充分挖掘空间资源,已经成为第五代移动通信系统(5th generation mobile communication system, 5G)物理层的关键技术[1-2]。为了满足对于超高传输速率和巨连接的需求,超大规模MIMO成为了下一代网络的候选关键技术。
网络实测结果显示,与传统多天线阵列相比,在超大规模MIMO通信场景下,无线传输信道中存在着球面波特性[3]。针对点对点的均匀线性天线阵列,文献[4]提出了一种包含球面波前的大规模MIMO三维信道模型,并通过数值仿真分析了天线阵元位置对信道空间相关性的影响。研究结果表明,空间相关性随着发射端天线阵元间隔的增加而减少,随着接收端天线阵元间隔的增加而呈现波动性。文献[5]在文献[4]的基础上,提出了一种包含球面波前的二维椭圆信道模型,不同于文献[4]中到达角度(angle of arrive, AOA)和发射角度(angle of departure, AOD)相互独立的假设,这里假设AOA和AOD相互关联,研究结果表明,球面波模型中大规模MIMO的空间相关性与平面波模型中的相关性极为不同。在点对点均匀线性阵列中的大规模MIMO直射环境中,基于计算机仿真,文献[6]给出了平面波与球面波模型中信道容量的对比,研究结果表明,使用球面波模型,即使在直射信道中,大规模MIMO信道容量也会随着天线数的增加而增加,并且它能达到适宜传播环境中的容量上界,然而平面波模型中的大规模MIMO信道容量不会随着天线数的增加而增加。
文献[3-6]主要围绕信道测量、信道建模和信道容量展开研究,并未针对超大规模MIMO中包含球面波特征的传输理论方法展开研究,忽略了其对系统设计的影响。在超大规模MIMO中,已知理想信道状态信息非常重要,但在实际通信场景中,由于导频污染、信道估计误差、反馈延迟和量化误差的存在,并不能获得理想的信道状态信息,这导致大规模MIMO性能下降。文献[7]提出一种基于统计信道状态信息的多用户MIMO传输方案,研究结果表明,与瞬时信道状态信息相比,统计信道状态信息变化缓慢,并且对于误差和反馈延时具有更强的鲁棒性。因此,研究基于统计信道状态信息的多用户MIMO传输引起了广泛关注[8-9]。
本文基于球面波模型,利用统计信道状态信息,研究了多用户超大规模MIMO中包含球面波特征的最优传输设计,给出了包含球面波特征的最优发射策略的闭式表达式,分析了影响最优传输的关键特征参数。研究结果显示,最优传输完全由用户与基站的仰角φ、方位角θ、天线间距d、天线数M、基站高度h所决定。为了解决用户与波束误匹配问题,本文提出了一种基于贪婪思想的低复杂度的用户调度策略。理论和仿真结果显示,所提传输策略能以较低复杂度达到近似最优性能。
1 系统模型
本文研究多用户超大规模MIMO系统中包含球面波特征的最优传输设计问题,系统模型如图1所示。
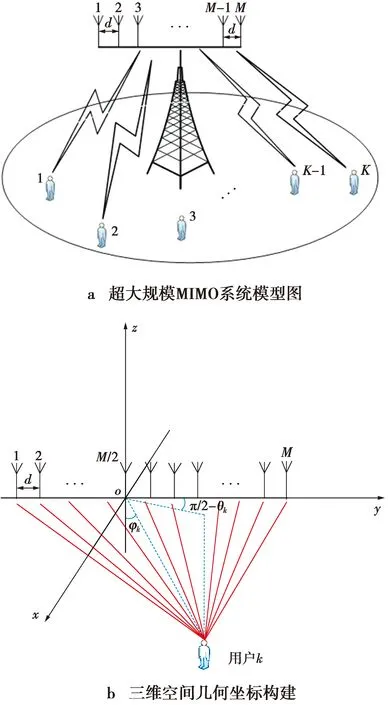
图1 单小区多用户超大规模MIMO系统模型图Fig.1 Single cell multi user large scale MIMO system model
图1a中,基站端部署M根线性阵列天线且同时服务于K个单天线用户。不失一般性,可构建三维几何坐标,见图1b。图1b中,阵列天线沿y方向排布,基站中心轴沿z轴放置,第M/2根天线位于坐标原点,第k个用户到原点的连线与z轴夹角为φk,其与正x轴之间的方位角为θk。此外,基站高度为h,天线间的间隔为d。基于此设置,第m根天线的坐标可以表示为(0,(m-M/2)d,0),第k个用户的坐标可以表示为(htanφkcosθk,htanφksinθk,-h)。发射端采用等功率分配方案,第k个用户处的接收信号可以表示为

(1)
(1)式中:yk表示第k个用户的接收信号;ρ=P/M为系统平均信噪比,P为发射端发射信号的总能量;hk∈C1×M表示发射天线到第k个用户的信道;xk∈CM×1为第k个用户预处理后的发射信号;nk表示均值为零、方差为1的高斯白噪声。
在实际传播环境中,信道同时包含直射(line of sight, LOS)传播与非直射(non line of sight, NLOS)传播2部分,其信道hk可建模为
(2)
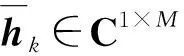
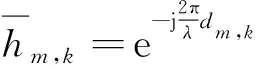
(3)
(3)式中:λ表示电磁波的波长;dm,k表示基站第m根天线到第k个用户间的传播距离,dm,k近似表示为
(4)
2 包含球面波特征的最优传输设计
在本节中,利用统计信道状态信息,基于信号泄露噪声比(signal to leakage and noise ratio, SLNR)最大准则,给出了超大规模MIMO中包含球面波特征的最优发射方向的闭式表达式。进一步,为了避免波束与用户间的误匹配,提出了一种低复杂度的用户调度方案。
设第k个用户的发射方向为wk∈CM×1且满足‖wk‖=1,从而第k个用户的发射信号表示为
xk=wksk
(5)
(5)式中:sk表示第k个用户的发射信息,且|sk|2=1。结合(1)式,系统的信道容量可表示为
(6)
从(6)式可以看出,为获得最大系统容量,需要对发射端最优发射方向进行优化设计。但由于存在耦合现象,通过信干噪比[12](signal to interference plus noise ratio, SINR)直接求解最优的发射方向存在一定难度。为了解决耦合问题,基于SLNR最大准则求解最优的发射方向,SLNR表示用户接收到的波束能量与泄露到其他用户的波束能量之比,其中,第k个用户的SLNR为[13-14]

(7)
(7)式中,ρ|hjwk|2表示第k个用户的波束泄露到其他用户的功率,其越小,SLNR越大,发射信号在期望方向上越集中,用户间干扰越小。基于SLNR最大准则,利用统计信道状态信息,超大规模MIMO中包含球面波特征的最优发射方向由定理1决定。
定理1利用统计信道状态信息,当特征参数满足条件
(8)
则超大规模MIMO中包含球面波特征的最优传输方向为
[eη(1-M/2)+(1-M/2)2μ,eη(2-M/2)+(2-M/2)2μ,…,eη(m-M/2)+(m-M/2)2μ,…,eη(M-M/2)+(M-M/2)2μ]T
(9)
证明利用统计信道状态信息,推导出(7)式中SLNR的下界,然后使SLNR下界最大,即可得到定理1。
从定理1可以看出,当给定电磁波波长λ、天线间距d、天线数目M、天线高度h,大规模MIMO中包含球面波特征的最优发射方向完全由用户与阵列天线的仰角φ、水平方位角θ所决定。进一步,这2个参数本质上由用户所处位置决定,这意味着最优发射策略与用户所处位置有关。因此,采用用户调度策略选取合适用户进行通信可以有效提升所提发射策略的效率,避免波束与用户的误匹配。
作为对比,文中同时给出了基于平面波建模的超大规模MIMO的最优发射方向,由定理2决定。在此,同样基于SLNR下界最大准则,利用统计信道状态信息进行定理推导。
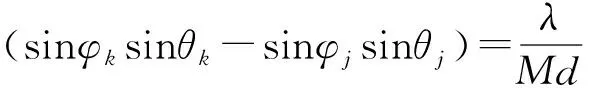
[eη(1-M/2),eη(2-M/2),…,eη(M-M/2)]T
(10)
从定理2可以看出,由于忽略了部分三维特性,采用平面波模型获得的多用户最优发射方向与采用球面波模型存在较为明显的不同。这说明,采用平面波这样一种简化模型会导致多用户最优发射方向出现一定程度上的误判,需采用球面波模型才能给出更为正确的评估。
为提高发射策略的效率,避免波束与用户间的误匹配,本文进一步开展了用户调度策略的研究。基于穷举搜索思想的用户调度策略是一种最简单的算法,该算法利用穷举搜索思想,遍历所有的用户组合,计算出每一种用户组合的传输速率,选取传输速率最大的用户组合,具体实现如下。
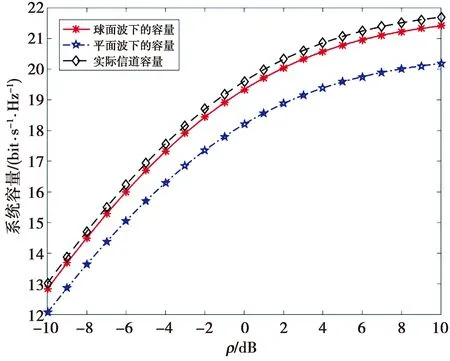
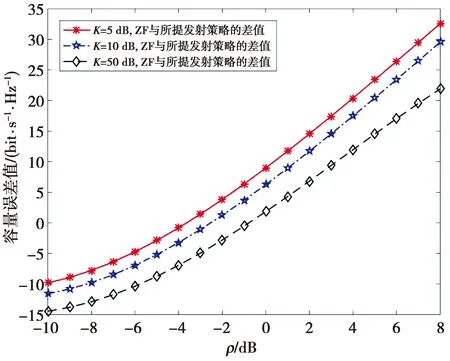
已知激活的用户数为Nu,总的用户数为K(Nu s.t.Φtmp=[j1,j2,…,jNu],j1,j2,…,jNu=1,2,…,K (11) 具体的用户调度策略见算法1。 算法1基于穷举搜索的用户调度策略 目标:Φ 初始化:Cmax=0 1:forj1,j2,…,jNu≤K 2:Φtmp=[j1,j2,…,jNu] 3: 计算C(Φtmp) 4: ifC≥Cmax 5:Cmax=C 6:Φ=Φtmp 7: end if 8: end for 输出:Φ 基于穷举搜索的用户调度策略能够给出系统的最优用户组合,但用户较多时,算法复杂度高,效率低。为降低用户调度策略的算法复杂度,本文提出了一种基于贪婪思想的低复杂度用户调度策略。该算法利用贪婪的思想逐渐选取使当前系统传输速率最大的用户。已知Φtmp为选择用户集合,Nu为激活用户数,C为当前系统传输速率,Φ为最优的用户集合。初始化选择用户集Φtmp为空,最优的用户组合Φ为空,第1个用户选择传输条件最好的用户,将所选用户从用户集U=[1,2,…,K]中删除并加入选择用户集Φtmp中,第2个用户的选择需遍历用户集中每个用户,加入当前选择用户集,计算用户集中每个用户加入当前选择用户集的传输速率,挑选使当前选择用户集传输速率最大的用户加入选择用户集,并从用户集中删除。其余用户选择方式与第2个用户选择方式类同,依次选择,直至选出所需要的用户数。基于贪婪思想的用户调度策略的具体过程如算法2。 算法2基于贪婪思想的用户调度策略 目标:Φ 初始化:Φtmp、Φ为空矩阵 2: 从U中删除第k列 3:Φtmp(1)=k 4: for 2≤a≤L 5:fori 6:Φ=Φtmp 7:Φtmp(a)=U(i) 8: ifC(Φtmp)>C(Φ) 9:Φ=Φtmp 10: temp=i 11: end if 12: end for 13: 从U中删除第temp列 14:end for 输出:Φ 基于贪婪思想的用户调度策略选取第1个用户需计算K次,选取第2个用户需计算(K-1)次,依次类推,选取第L个用户仅需要计算(K-L+1)次。选取L个用户总的计算次数为(2K-L+1)L/2,当用户数K比较大时,其计算次数远低于穷举搜索的计算次数,且在实际应用中更容易实现,复杂度对比如表1所示。 表1 不同用户调度策略的计算次数对比Tab.1 Numbers of comparisons for different user scheduling strategies 本节通过数值仿真来评估所提策略的有效性。在仿真中,考虑每个用户的莱斯因子K为30 dB,基站高度h=10 m,天线间距d=0.02 m,基站天线数M=128,每个用户的水平夹角θk在(0,2π)内,垂直仰角φk在(0,π/2)内,单小区中有8个用户,选取5个用户进行通信。 图2给出了利用统计信道状态信息获得的超大规模MIMO多用户系统中球面波建模和平面波建模的最优发射策略的性能对比。从图2可以看出,球面波模型获得的系统容量更加接近于系统的真实容量,而平面波模型获得的系统容量与真实的系统容量存在较大的误差,会在一定程度上导致误判,这一结论与本文的理论分析一致。 图2 球面波建模和平面波建模的最优发射策略的性能对比Fig.2 Performance comparison of the optimal transmission strategy for spherical wave modeling and plane wave modeling 采用用户调度策略可以提高发射策略的效率,避免波束与用户间的误匹配。为比较不同用户调度策略的性能,图3给出了基于贪婪思想、基于穷举搜索思想以及未进行用户调度3种策略下的系统容量对比。从图3可以看出,相比于基站未进行用户调度,采用了用户调度的传输方案的系统具有更好的性能。这是因为采用用户调度策略避免了波束与用户的误匹配,从而提升了系统的频谱利用率。此外还可以看出,基于穷举搜索思想的用户调度策略的传输性能要略好于本文方法的传输性能。但本文方法复杂度更低,更容易实现,在兼顾性能的同时,又降低了实现复杂度。因此,与未进行用户调度的传输方法和基于穷举搜索思想的用户调度策略的传输方法相比,具有更好的应用前景。 图3 用户调度性能比较Fig.3 Performance comparison of user scheduling 本文采用了基于统计信道状态信息,以SLNR最大为准则的预编码方案。此外,与目前性能最优良的脏纸编码(dirty paper coding, DPC)相比,线性的迫零(zero forcing, ZF)预编码实现简单,并且和DPC的性能差距可以忽略不计,因此更为实用[14-15]。图4给出了基于瞬时信道状态信息的ZF预编码和本文采用的预编码方案的优劣性的对比。其中,图4中的容量误差值表示基于ZF预编码获得的系统容量与基于所提预编码方案获得的系统容量的差值。从图4可以看出,在低信噪比下,使用本文所提的最优发射策略明显优于ZF预编码方案,另外,虽然在高信噪比条件下,ZF预编码方案获得的系统容量要高于本文所提预编码方案,但是本文所提预编码方案需要的信道状态信息的反馈开销要小得多,且计算复杂度更低,同时当莱斯因子K比较大时,本文所提的预编码方案只需少量的反馈信息就能达到好的性能。 图4 所提发射策略与基于瞬时信道状态信息的ZF的容量误差分析Fig.4 Capacity error analysis of the proposed transmission strategy and ZF precoding algorithm based on instantaneous channel state information 本文利用统计信道状态信息,基于SLNR最大准则,研究了多用户超大规模MIMO中包含球面波特征的最优传输方法。首先,给出了超大规模MIMO中包含球面波特征的最优发射策略的闭式表达式,解决了多用户超大规模MIMO中包含球面波特征的最优发射问题。其次,为了避免波束与用户的误匹配,提出了一种基于贪婪思想的低复杂度用户调度策略。最后,通过理论分析和仿真结果显示,所提传输策略能以较低复杂度达到近似最优性能。
3 仿真分析

4 结 论

