高普朗特数流体圆柱坐标下自然对流数值模拟研究1
邵倩倩,王敏,许诺,梁飞华
(1.广东石油化工学院 石油工程学院,广东 茂名 525000;2.北京计算科学研究中心,北京 100193)
在石油储运行业中,储罐内油品的传热问题是圆柱坐标下自然对流在工程上的典型应用之一。相较于其他流体,石油产品的特征是普朗特数(Pr)较高。因此,对高Pr流体在圆柱坐标下自然对流规律进行研究是进一步深入解决油品储存过程中所涉及的各种流动与传热问题的基础。如,以圆柱坐标下自然对流为基础,进一步研究储罐和管道内油品的温度分布,并根据油品闪点、沸点、凝点等指导油品的节能生产与储运安全[1-3];以不同条件(如昼夜变化、天气变化等)下储罐内油品温度分布为基础,可以进一步研究油品的蒸发损耗,同时为减小蒸发损耗提供宝贵决策[4-6]。
自然对流问题的温度场与速度场受物理区域的几何特征、Pr、瑞利数(Ra)以及边界条件等共同影响。两同心圆筒壁间区域是常见的用于研究圆柱坐标下自然对流问题的几何形状。Powe等[7]采用数值计算方法研究了不同Ra下水平圆柱环形空腔内的自然对流,其中Pr选为0.7。Kuehn等[8]采用实验和数值模拟对水平圆柱环形空间内的自然对流进行研究,环形宽度与内径的比值为0.8,Pr选为0.7、5.45,Ra范围为2.11×104~9.76×105,其实验结果与数值计算结果吻合良好。Basant等[9]对不对称加热或冷却的两个立式圆筒之间的自然对流进行研究,分析了浮力分布参数的影响,获得了瞬态自然对流的半解析解。Kumar等[10]关注立式圆柱环形空间,对Pr为0.7、Ra为10~106、不同高径比几何特征下的自然对流传热与流动进行研究。调研发现,以往对圆柱坐标下自然对流问题的研究多针对低Pr流体展开。本研究以Pr=1000为例,采用数值计算方法模拟两同心圆筒壁间的自然对流。内圆筒高温、外圆筒低温、顶部和底部绝热,Ra取为1.0×103、1.0×104、1.0×105及1.0×106。采用加密网格和多重网格算法,得到计算区域的温度场、流场以及流函数分布等,基于数值计算结果研究高Pr流体圆柱坐标自然对流规律,分析Ra对温度场与流场的影响。
1 数值计算方法
1.1 物理问题及简化
本研究物理区域(如图1a所示)为内圆筒与外圆筒之间的区域。考虑三维圆柱坐标下,物理量沿周向方向(图1a中θ所在的方向)的变化可近似忽略,本文将三维圆柱坐标简化为二维圆柱坐标(见图1b)。其中,x方向为高度方向,朝上为正方向;r坐标指定朝外圆筒为正方向,坐标原点位于圆柱底的圆心。对于本研究计算区域,径向上长度(即内、外圆筒壁径向上的间距)为l,高度方向长度为h。
1.2 控制方程
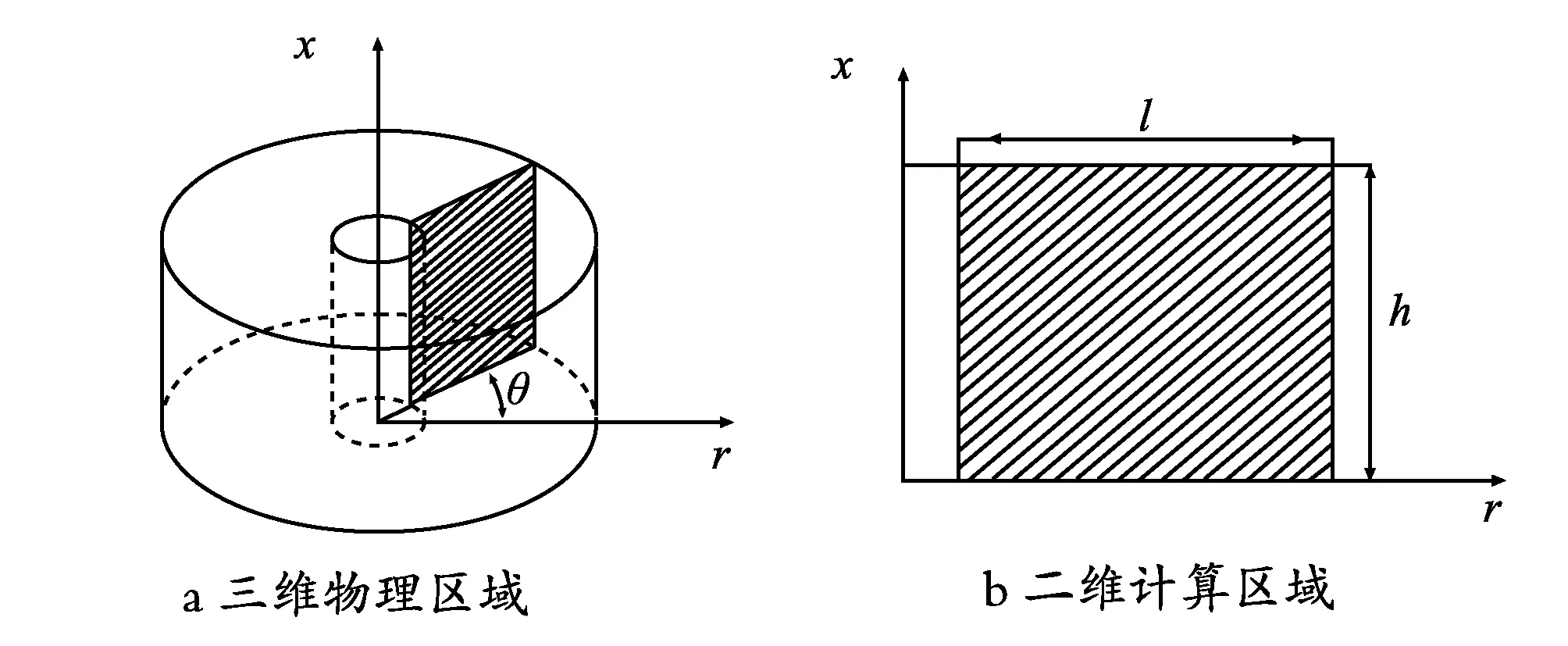
图1 三维圆柱坐标物理问题及其二维简化
圆柱坐标下自然对流的控制方程包括连续性方程、x方向动量方程、r方向动量方程以及能量方程,其分别为
(1)
(2)
(3)
(4)
式中:r、x分别为r方向、x方向坐标值,m;ρ为密度,kg/m3;cp为比热容,J/(kg·K);p为压力,Pa;g为重力加速度,取9.81 m/s2;μ为动力黏度,Pa·s;β为热膨胀系数,1/K;λ为导热系数,W/(m·K);T为温度,K;u和v分别为x方向、r方向的速度分量,m/s。
引入无量纲量R=r/l,X=x/l,U=ul/υ,V=vl/υ,P=pl2/ρυ2,Θ=(T-Tc)/(Th-Tc),Pr=ρcpυ/λ,Ra=Gr·Pr=ρgβcp(Th-Tc)l3/λυ(Gr为格拉晓夫数,定义为Gr=gβ(Th-Tc)l3/υ2;l为计算区域的宽度,m;υ为运动黏度,m2/s;Th、Tc分别为高温边界和低温边界的温度,K)。
对式(1)~(4)进行无量纲化,可得:
(5)
(6)
(7)
(8)
1.3 数值计算方法及验证
为了获得更高的计算精度,采用涡量-流函数法来计算流函数,当流函数的残差小于1.0×10-10时,计算结果认为是收敛的;计算区域采用1026×1026的非均分网格进行离散,网格足够密,所得结果具有高精度;采用多重网格算法来提高数值计算速度[11, 12]。
采用本文计算方法对经典文献[10]中问题进行计算,其中Pr=0.7,Ra=2×105。所得结果与文献[10]中结果进行比较,如图2所示。其中R1为无量纲内半径,R2为无量纲外半径。

图2 文献[10]与本研究数值计算方法的准确性
由图2可知,采用本文计算方法所得结果与文献[10]中结果吻合较好,因此,本研究的数值计算方法被认为是精确有效的。
2 计算结果与分析
2.1 计算条件
本研究中考虑的温度边界条件如图3所示,其中内边界为高温(Th)边界,外边界为低温(Tc)边界,上边界和下边界均为绝热边界 ∂T/∂x=0。各边界速度设置为无滑移条件,即各边界上u=0,v=0(即U=0,V=0)。Ra设为1.0×103、1.0×104、1.0×105及1.0×106,Pr设为1000,代表油品这一类高Pr数流体。无量纲内半径为R1=0.1;无量纲外半径为R2=1.1;无量纲高度为H=1。

图3 二维圆柱坐标下自然对流温度边界条件
2.2 温度场与速度场分布
图4为不同Ra下计算所得的X-R坐标下的温度场与速度场,给出的参照速度矢量单位为m/s。

图4 不同Ra下的温度场与速度场
由图4可知,(1)高温流体对流到低温区域,低温流体对流到高温区域,流体在区域内呈现顺时针旋转。(2)中心区域流速较小,这是由于中心区域流体温差小,密度差也小,流体对流较慢。边界处速度较大则是由于较大的温差产生的大的密度差,使流体运动剧烈。(3)Ra增大,自然对流增强,流体流动更加剧烈,速度整体增大。(4)当Ra增大时,高温区域从内圆筒向外圆筒及上部转移,一方面,内外圆筒温差的作用,热量不断地由内圆筒传到外圆筒;另一方面,对流使得高温流体向上方移动。
2.3 流函数场
图5为不同Ra下计算所得的流函数场。由图5可知,(1)不同Ra下流函数场均清晰地显示一个主涡。(2)Ra对流函数的分布和数值均有很大的影响,当Ra较小时,流函数的等值线形状较为规则,不同等值线近似同心均匀分布;当Ra增大时,各等值线形状差别加大,且形状变得不规则,流动变得更加复杂,表现出越来越明显的湍流特征。(3)当Ra增大时,主涡的位置向低温边界及上边界转移,即向图中的右上角移动,同时,最大流函数数值明显增加。

图5 不同Ra下的流函数分布(图中所标数字代表流函数数值)
为了更准确地展示这一规律,表1给出了不同Ra下主涡中心的坐标以及对应的最大流函数值。从表1可以直观地看到,当Ra增大时,主涡中心的R坐标以及X坐标均增大,最大流函数值更是明显地增大。

表1 不同Ra下计算所得主涡中心坐标以及最大流函数值Ra=1.0×103Ra=1.0×104Ra=1.0×105Ra=1.0×106主涡中心R坐标值0.64250.66880.81040.9413主涡中心X坐标值0.51420.54540.59910.7446最大流函数值0.00050.00220.00490.0080
2.4 Ra对温度场与流场的影响
图6展示了Ra对计算区域两条中心线(X=1/2,R=(R1+R2)/2)上温度分布的影响,图7展示相应的Ra对速度分布的影响(图7仅给出垂直于各中心线的速度分量的情况)。
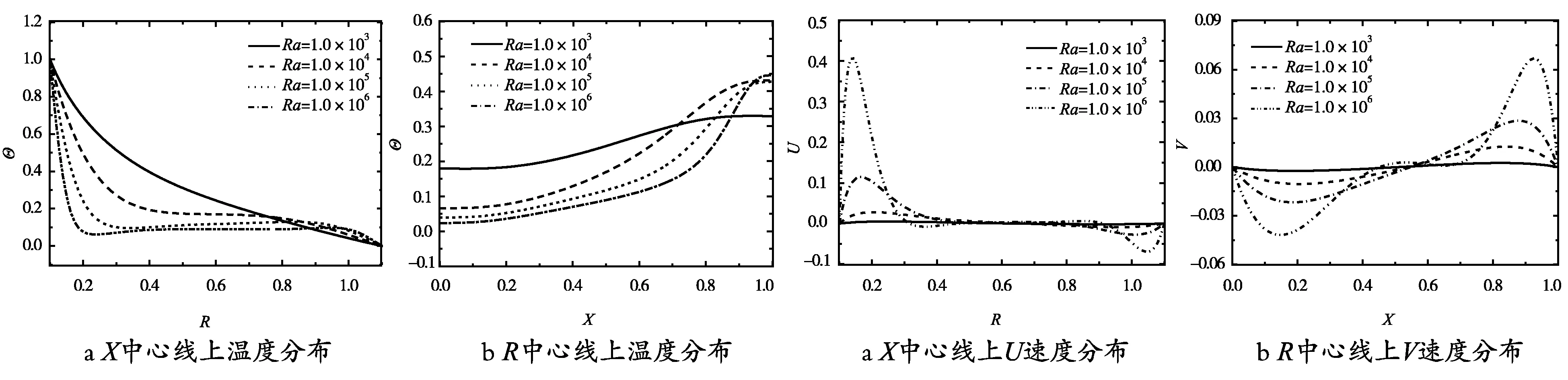
图6 不同Ra下计算区域两条中心线上温度分布 图7 不同Ra下计算区域两条中心线上速度分布
由图6可知,对于Θ~R分布曲线,当Ra较小时,从内圆筒到外圆筒沿着X=1/2中心线,温度逐渐降低,其分布接近对数分布,这是由于低Ra下,自然对流较弱,热传导占主要地位,传热过程类似于纯导热过程。随着Ra增大,X=1/2中心线上Θ~R分布越来越偏离对数分布。当Ra较大时,在内圆筒处温度急剧下降,远离内圆筒处,温度分布近似均匀。对于Θ~X曲线,高温存在于X较大的区域,即上部区域,这是高温流体向上运动导致的。而Ra增大使得高温流体向上聚集的现象更为明显,表现为沿R=(R1+R2)/2这条中心线,上边界附近温度梯度随着Ra的增加而增大。
由图7可知,由于边界无滑移速度条件以及自然对流的作用,在各边界附近,速度均表现为先增大后减小的分布特征,速度梯度随Ra增大而变大;Ra对速度大小影响亦十分明显,当Ra增大时,流速显著增大。例如,Ra=1.0×106时,中心线X=1/2上最大U速度约为Ra=1.0×103时的85倍。
为了直观显示自然对流的强弱,给出努塞尔数(Nu)在内外边界上的分布情况,见图8。其中Nu1为高温边界上Nu,Nu2为低温边界上Nu。图8a、图8b分别为高温边界、低温边界上Nu沿X方向的分布情况。由图8可知,在高温内边界及低温外边界上,Nu均随着Ra增加而显著增加,即对流换热增强。

图8 不同Ra下高温边界及低温边界上Nu分布
3 结语
使用数值计算的方法对高Pr流体在圆柱坐标下的自然对流问题进行研究,基于精密网格划分,采用有限容积法并利用多重网格算法来提高计算效率,借助经典文献中的数据验证了本文数值计算方法的精确可靠。研究得到了不同Ra下自然对流的温度场、速度矢量场以及流函数场的分布情况,并对中心线上的温度分布、速度分布以及高温边界和低温边界上的Nu分布进行了分析,主要结论如下:(1)Ra对温度场和流场均有较大的影响,反映自然对流的强弱;(2)当Ra增大时,高温流体对流到低温区域、低温流体对流到高温区域的现象更加剧烈,使上下区域温度分层现象更加明显,且对流换热增强,表现为明显增大的Nu;(3)Ra增大,速度整体上增大,且最大流函数值增加,主涡位置向低温边界及上边界移动。

