基于AMMI 模型的花生品种产量稳定性及试点代表性分析

董晓月荆建国聂红民陈翠霞李 洁李振华马金娜谷献锋杨宜红

(濮阳市农业科学院,河南 濮阳 457000)

作为新品种审定、推广的前提条件,区域试验是衡量新品种丰产性、稳定性和适应性的重要手段[1～2]。 品种的产量受基因型、环境及二者互作效应的影响。 利用方差分析和多重比较可以评价品种的丰产性,但不能准确评价不同品种之间的差异性,这是因为没有考虑到基因型和环境互作效应对品种产量的影响[3]。 以前,有学者曾提出可以利用线性回归模型解释基因型和环境的互作效应[4], 但是该模型对互作效应的解释比例很小,分析所得结果误差较大。 AMMI(Additive main effects and multiplicative interaction)模型是主效、可加互作可乘模型[5],该模型将方差分析和主成分分析相结合,同时利用双标图和互作效应值对基因型和环境互作效应进行解释,直观、定量地分析品种间产量的差异以及试点鉴别力的大小[6]。AMMI 模型被广泛应用于水稻、小麦、玉米、棉花、油菜等作 物 区 域 试 验 的 分 析[1,7～13]。 近 年 来,GGE(Genotype main effects and genotype environment interaction)基因型和环境互作模型逐步应用在作物区域试验分析中,也能够直观有效地评价基因型和环境之间的互作[14]。 GGE 模型是在AMMI 模型的基础上发展而来的。 AMMI 侧重分析品种稳定性[15～16],GGE 则侧重分析品种适应性[17];同时还有文章表明,AMMI 模型在稳定性和环境鉴别力分析上具有与优势,GGE 双标图法在适应性分析上具有优势[14]。 基于此,本文选用AMMI 模型分析花生荚果产量,评价参试品种的丰产性、稳定性和试点鉴别力,从而筛选出高产稳产的花生新品种及对应适宜种植的生态区,为花生新品种的推广提供参考。

1 材料与方法

1. 1 试验材料及设计

本文数据来自2020 年国家北方片大粒3 组的试验结果,该组试验参试品种13 个、承试试点18 个,对品种、试点进行赋码,品种、试点及对应的平均产量详见表1。 试验播种时间在5 月10 日左右,小区长5. 5 m、宽2. 40 m,小 区 面 积 13. 2 m2, 播 种 密 度 15 000 穴/hm2, 穴 距16.7 cm、行距40 cm。 随机区组设计,重复3 次,田间管理参照各地种植习惯。 收获时间在9 月10 日左右,成熟后按照小区收获,并进行晾晒、称重。

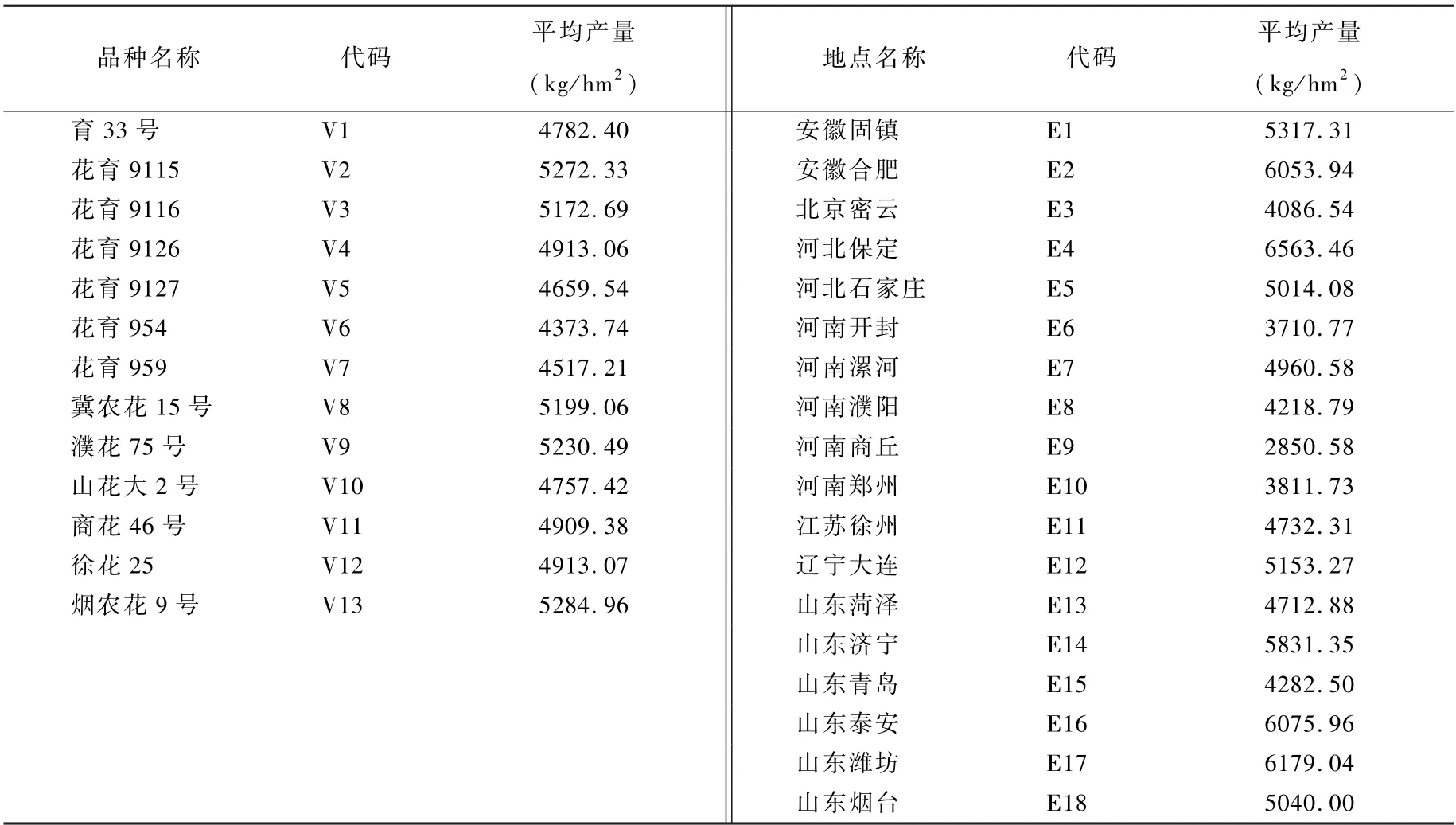
表1 参试品种名称、试点及其平均产量

1. 2 数据分析

参照王磊等方法进行AMMI 模型分析[18],参照张泽等方法计算稳定性参数[19]。 利用Excel 2010 和DPS 7.05数据系统软件处理数据。

2 结果与分析

2. 1 产量联合方差、线性回归和AMMI 模型分析

由表2 可知,按照联合方差法分析,基因型间平方和仅占总平方和的6. 70%,而环境间平方和占75. 17%,二者交互作用的平方和占11. 59%,环境间、基因型间及其交互作用的差异均达到极显著性水平,说明品种之间差异明显;因环境间变异占比大,且交互作用的变异比基因型间变异大,所以必需分析品种稳定性。

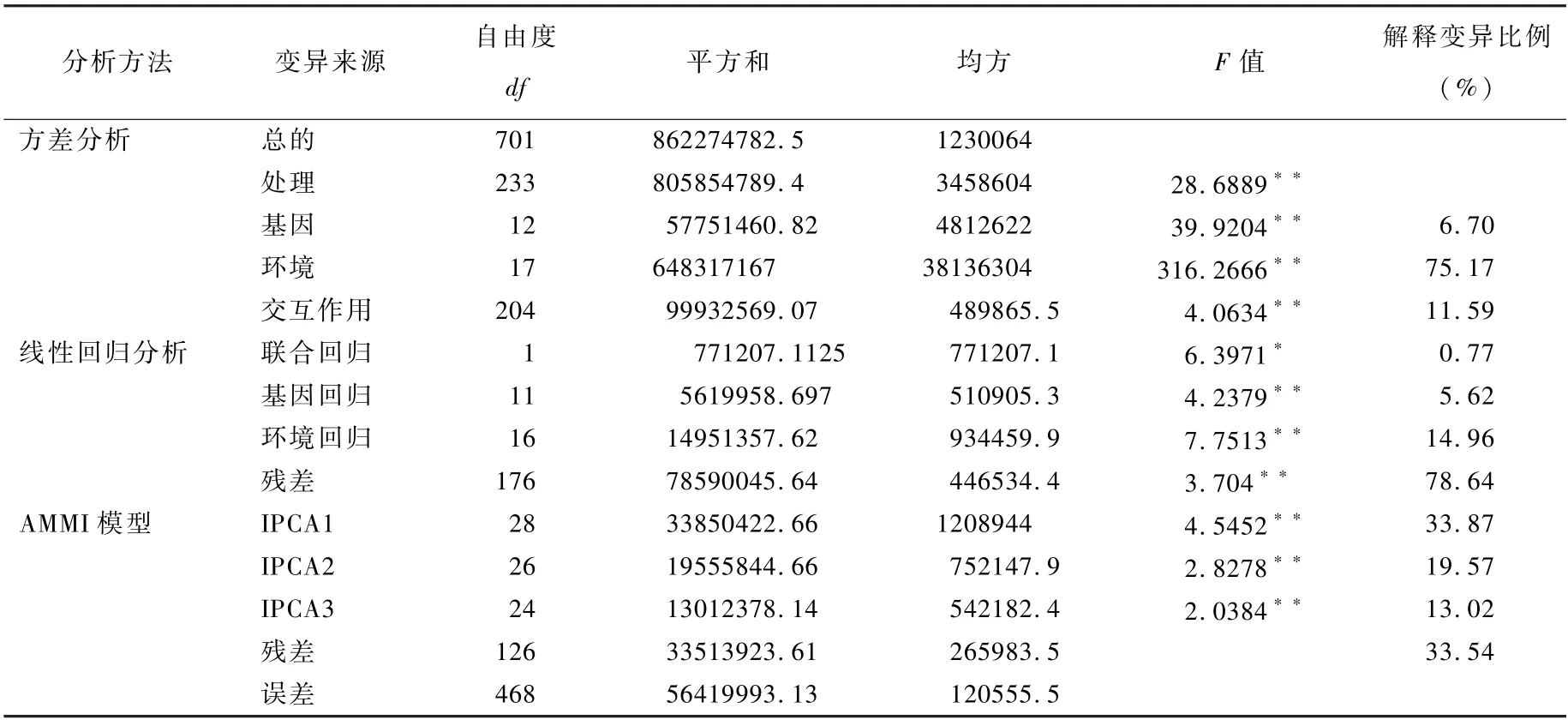
表2 花生区域试验产量方差分析、线性回归分析及AMMI 模型分析结果

按照线性回归法分析,联合回归、基因回归、环境回归三者之和占交互作用比为21. 36%,而残差占比较大,达78.64%,且残差差异达到极显著性水平,这说明线性回归模型对互作效应解释较少,不适合拟合本试验数据。

按照AMMI 模型分析,基因型和环境互作分解为3 个存在极显著差异的乘积相,即IPCA1、IPCA2、IPCA3,其余不显著的合并为残差。 IPCA1、IPCA2、IPCA3 的平方和分别占互作平方和的33. 87%、19. 57%、13. 02%,累计解释互作平方和的66. 46%,这说明AMMI 模型可以有效、合理地解释基因型和环境的互作。

2. 2 AMMI 双标图分析品种稳定性和试点鉴别力

以平均产量为横坐标、IPCA1 为纵坐标绘制AMMI 1双标图。 从图1 可知,在横坐标轴方向上,品种图标分布相对集中,分布范围4 000 ～5 500 kg/hm2;试点图标分布较分散,分布范围2 500 ～7 000 kg/hm2,这说明试点间产量变化幅度比品种间产量变化幅度大。

在纵坐标轴方向上,品种距0 值水平线上的距离愈近,品种稳定性愈高;试点距0 值水平线上的距离愈远,试点的鉴别力愈强[16,20]。 从图1 可得,品种V6(花育954)的稳定性最好,其次是品种V10(山花大2 号)、V12(徐花25)、V1(花育33 号)、V7(花育959)稳定性稍差,品种V3(花育9116)和V11(商花46 号)稳定性较差;试点E15(山东青岛)鉴别力最强,其次是试点E16(山东泰安)、E17(山东潍坊)、E7(河南漯河)、E18(山东烟台)、E3(北京密云)和E2(安徽合肥),试点E8(河南濮阳)鉴别力最弱。

图1 AMMI 1 双标图

以IPCA1 为横坐标、IPCA2 为纵坐标绘制AMMI 2 双标图。 在AMMI 2 双标图中,品种离原点愈近,品种的稳定性愈好;试点离原点愈远,鉴别力愈强[20,21]。 从图2 可知,品种V5(花育9127)、V10(山花大2 号)、V9(濮花75号)、V1(花育33 号)稳定性较好,品种V6(花育954)、V3(花育9116)、V11 V11(商花46 号)稳定性较差;试点E15(山东青岛)鉴别力最强,其次是试点E13(山东菏泽)、E17(山东潍坊)、E2(安徽合肥)和E16(山东泰安)、E7(河南漯河)、E1(安徽固镇)、E11(江苏徐州),试点E12(辽宁大连)和E14(山东济宁)鉴别力最弱。 因AMMI 2双标图解释互作效应为53. 44%,而AMMI1 双标图解释互作效应仅为33.87%,所以,AMMI 2 双标图推断的结果比AMMI 1 双标图更具全面、可靠。

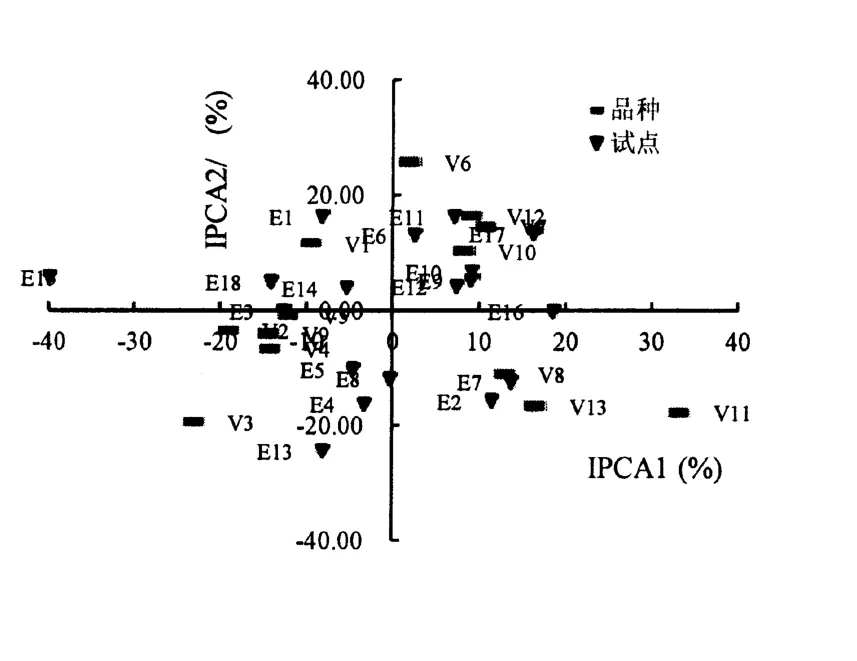
图2 AMMI 2 双标图

2. 3 稳定参数法分析品种稳定性和试点辨别力

稳定性参数法Dg(e)是一种能够量化品种稳定性和试点鉴别力大小的方法, Dg 值愈小,说明品种愈稳定;De值愈大,说明试点对品种的鉴别力愈强[20,22]。 据表3 可知,品种稳定性参数大小依次是:V11＞V3＞V6＞V10＞V2＞V13＞V5＞V1＞V7＞V12＞V4＞V8＞V9,而品种稳定性大小则为V9＞V8＞V4＞V12＞V7＞V1＞V5＞V13＞V2＞V10＞V6＞V3＞V11,V9、V8、V4、V12、V7 在各试点有较好的稳定性。 根据品种的平均产量、稳定性参数综合判断,V9(濮花75号) V8(冀农花15 号)、V4(花育9126)、V12(徐花25)属于高产稳产型品种,分别较对照V1(花育33) 增产9.37%、8.71%、2.73%、2.73%; V2(花育9115)、V3(花育9116)、V11(商花46 号)、V13(烟农花9 号)是高产、稳定性较差的品种; V5(花育9127)、V7(花育959)是稳定性较好、产量较低的品种; V6(花育954)、V10(山花大2号)是低产、稳定性较差的品种。

表3 花生区域试验品种在显著互作主成分轴上的得分及稳定性参数

据表4 可知,试点鉴别力参数排序依次是:E15＞E16＞E13＞E2＞E3＞E17＞E7＞E1＞E11＞E4＞E10＞E18＞E6＞E8＞E4＞E9＞E5＞E12,试点E15 鉴别力最强,其次是试点E16、E13、E2,试点E12 鉴别力最弱。 AMMI 双标图、稳定性参数两种方法得出,试点E15(山东青岛)鉴别力最强;试点E13(山东菏泽)、E2(安徽合肥)鉴别力较强;其次是试点E16(山东泰安)、E17(山东潍坊)、E7(河南漯河)、E1(安徽固镇)、E11(江苏徐州);试点E14(山东济宁)、E5(河北石家庄)、E12(辽宁大连)鉴别力弱。

表4 花生在显著互作主成分轴上的得分及稳定性参数

2. 4 品种在试点上的特殊适应性分析

品种在试点的特殊适应性表现在品种和试点的交互作用上。 新品种在应用推广的同时,应分析基因型和环境互作效应产生的影响,尽量选择有利互作[20]。 与AMMI 双标图相比,Dge 互作效应值更能准确地体现出品种在试点的特殊适应性。 由表5 可知,各个品种与不同试点的互作效应值。,高产品种V13 与试点E8、E13、E16 有较大的正交互作用,与试点E1、E15 有较大的负交互作用,说明品种V13(烟农花9 号)在试点E8(河南濮阳)、E13(山东菏泽)、E16(山东泰安)有特殊适应性,而不适宜种植在试点E1(安徽固镇)、E15(山东青岛);同理,品种V2(花育9115)在试点E3(北京密云)、E15(山东青岛)有特殊适应性,而不适宜种植在试点E9(河南商丘)、E10(河南郑州);品种V9(濮花75 号)在试点E3(北京密云)、E8(河南濮阳)、E15(山东青岛)、E18(山东烟台)有特殊适应性,而不适宜在试点E7(河南漯河)、E16(山东泰安)种植。 其他高产品种与试点的适应性情况也可依次进行推断。

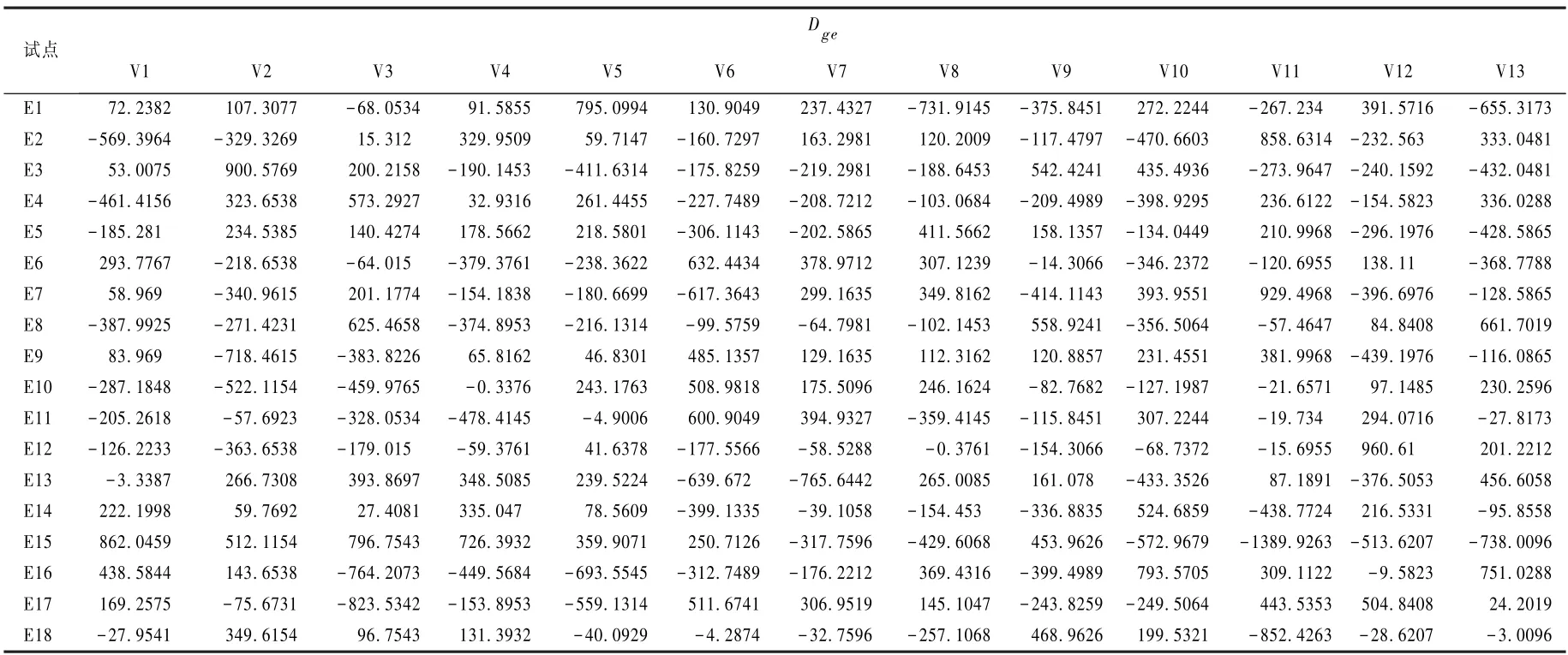
表5 品种与试点互作效应值(Dge)

3 结论与讨论

AMMI 模型分析结果表明,基因型、环境及二者互作效应对花生荚果产量的影响都达到极显著水平,基因型与环境互作效应虽小于环境效应,但却是基因型效应的1.73 倍,这与在小麦、大麦、玉米、油菜等作物得出的分析结果一致[20,23～25]。 这表明在选择、推广花生新品种时,要将环境因素放在首位,同时考虑基因型和环境的互作效应,即一方面选择适合品种推广的良好区域,另一方面筛选具有优良性状的品种,确保优良品种在适宜的生态区推广。 值得注意的是在18 个试点的品种间产量差异幅度19.38%～85.07%,这说明品种增产空间需要进一步挖掘。 AMMI 双标图在一定程度上对品种稳定性以及试点鉴别力进行了解释[25]。 在本研究中,AMMI1 双标图解释基因型和环境互作变异仅为33. 87%,AMMI 2 双标图解释基因型和环境互作变异仅为53. 44%,稳定性参数解释基因型和环境互作变异为66. 46%,所以利用双标图法和稳定性参数法得到的结果不完全一致[26]。 有研究表明,当IPCA≥3(IPCA 之间呈显著差异)时,双标图无法将基因型和环境互作效应全部有效地反映出来,此时应将存在显著关系的所有IPCA 利用起来计算稳定性参数,这样得到的品种稳定性差异、试点代表性更加真实、客观[21,27]。

不同花生品种在不同试点稳定性差别较大,且不同试点对不同花生品种的鉴别力相差也比较大。 13 个参试品种稳定性参数Dg 表现为濮花75 号最小(15. 03)、商花46 号最大(37. 94),两个品种相差1. 52 倍;18 个试点稳定性参数De 表现为辽宁大连最低(9.34)、山东青岛最高(40.50),两个试点相差3.34 倍,这一研究结果同样也适用在小麦等作物上[1]。 所以,实施花生区域试验时,一方面要选择代表性强的品种和试点环境,另一方面应该衡量试点的鉴别力;此外,还应尽量减少相似度高的品种和试点的设置。 本研究利用AMMI 双标图法和稳定参数综合分析, 13 个参试品种中,花育9126、冀农花15 号、濮花75 号、徐花25 属高产稳产品种,花育9115、花育9116、商花46 号、烟农花9 号属高产不稳产品种,花育9127、花育959 属稳产不高产的品种,花育954、山花大2 号是产量低、稳定性差的品种。 18 个试点中,山东青岛对品种鉴别力最强,山东菏泽、安徽合肥对品种鉴别力较强,山东济宁、河北石家庄、辽宁大连鉴别力弱,其余试点鉴别力一般。 因不同年份土壤墒情、气象因子以及病虫害等因素的综合影响,使得不同年份之间试验数据存在较大波动,影响了分析结果的准确性。 因此,今后应进行多年多点试验,综合分析试验结果,以便更加全面评定品种特性和试点鉴别力。