分级真空预压法处理疏浚淤泥的三维数值分析

刘洪波，周卫东，张志鹏

（1、广州环投增城环保能源有限公司 广州 511335；2、广州环保投资集团有限公司 广州 510330；3、上海大学力学与工程科学学院 上海 200444）

近年来，疏浚工程广泛开展于开挖新航道、清理现有港口、疏通河道与渠道等工程中，疏浚出来的疏浚淤泥可用于吹填造陆或填海等工程中。然而，疏浚淤泥大多由细土颗粒、水、有机物以及重金属组成，具有高含水率，高压缩性且基本无抗剪强度的特点［1］。因此，需要对疏浚淤泥处理后才能便于运输和后期的利用。真空预压作为一种有效的疏浚淤泥处理方式已在工程实践中被运用［2］，但在处理过程中细颗粒会向排水板迁移，导致排水板附近形成淤堵层或堵塞排水板滤膜，使得真空预压法处理效果受限［3-5］。

为解决真空预压过程中的淤堵问题，已有学者提出采用分级真空预压法来处理疏浚淤泥。YUAN 等人［6］研究发现，通过采用逐级施加真空荷载的方式处治疏浚淤泥可以有效缓解真空预压过程中排水板淤堵的情况，同时可以改善处理后土体的均匀性。武亚军等人［7］通过开展不同初始真空荷载下流泥加固的室内模型试验，从机制上探讨了初始真空荷载对分级真空预压法加固效果的影响。LIU 等人［8］通过三组不同真空梯度下的分级真空预压法的室内模型试验对比，发现20 kPa 的真空梯度下，分级真空预压法效果最优，40～50 kPa 的真空梯度下，分级真空预压法处理后土体排水最多。

除通过室内试验的方式来探究真空预压法的加固机理外，采用数值模拟软件建模分析也是一种有效的探究微观加固机制方式。INDRARATNA［9-10］结合改进的Cam-Clay 模型，描述了预制垂直排水板处理的软粘土的数值模拟中考虑了排水-土壤界面不饱和度的影响。SHI等人［11］采用离散元对真空预压过程中的排水板滤膜堵塞问题进行微观数值分析，结果发现膜上薄而密的土层是造成排水板堵塞的原因。雷华阳等人［12］采用PFC2D软件探究了不同颗粒组成土体的真空预压试验的颗粒流微观模拟，从微观角度对其加固机理进行解释。并且还探究了交替式真空预压法中颗粒的移动情况，发现土颗粒的交替式运动有效破除了淤堵层，有效抑制了“土柱”的形成。

综上可知，为解决真空预压过程中的淤堵问题，已有学者发现分级真空预压法能缓解真空预压处理过程中淤堵层的形成，且大多是从宏观指标验证该工法加固的有效性，鲜有从微观角度分析其加固机理。针对上述问题，本文采用颗粒流软件PFC3D建立三维模型，从微观角度分析分级施加真空压力对真空预压过程影响以及颗粒迁移的机理解释。

1 数值模拟过程

1.1 数值模拟方案

本文建立的三维模型尺寸及颗粒级配等都参照了刘飞禹等人［13］进行的分级真空预压联合间歇电渗法中分级真空预压试验部分。宽度参照一般整体式排水板宽度10 cm 进行建模，具体模型尺寸如图1 所示，其中长度为14 cm，宽度为10 cm，高度为18 cm。分级真空预压的模拟试验共设置4组，如表1所示。

图1 模型尺寸Fig.1 Model Size

表1 数值模拟方案Tab.1 Numerical Simulation Scheme

其中T1 为对照组，在计算步长至300 万步时，土体孔隙率基本趋于稳定，故以300 万步为基准进行T2～T4 分级时间点，数值模拟中分级的时间点参照文献［13］中的分级真空预压时间点。T2-T4 皆计算至远离排水板处监测点的孔隙率趋于稳定时停止，由于试验初期采用低真空压力进行排水，故采用分级真空预压法的模拟组别计算步长皆大于T1 对照组。T4 组别在0～120万步时施加20 kPa的真空压力，在120万～220万步时施加40 kPa的真空压力，在220万～600万步时施加80 kPa的真空压力，其余组别同理进行真空压力的施加。

1.2 模型建立

采用PFC3D5.0 软件建立模型，分析了分级真空预压下土颗粒迁移的规律。室内试验中采用疏浚淤泥进行试验，而疏浚淤泥包括粒径小于0.005 mm 的黏粒，由于软件的单元尺寸限制，若采用真实的黏粒颗粒大小生成三维颗粒，会导致生成的颗粒数目巨大而超出计算机计算能力范围，从而无法进行模拟计算，故实际的土颗粒大小无法取到实际的黏粒大小，而应进行相同倍数的放大。考虑到模型的尺寸大小，最终将土颗粒进行400 倍的放大，并且简化土颗粒的颗粒级配分布，将黏粒粒径小于0.005 mm的土颗粒都看作为0.005 mm，其余部分的粉粒粒径范围为0.005～0.02 mm，黏粒与粉粒的百分含量参照文献［12］在室内试验疏浚淤泥颗粒级配，分别为35%与65%，土体生成的孔隙率为0.7，不同粒径的颗粒位置随机分布。

在模型中，采用球单元（Ball）来模拟土颗粒，用墙单元（Wall）来模拟边界，用流体（Fluid）来模拟土中的水。模型中将左边界看作排水板的位置，根据试验方案设置不同的流体梯度来模拟不同真空负压，右边界统一设置为0 kPa，上下边界与前后边界不施加真空荷载，作为不透水边界。模拟考虑真空压力下土体径向固结作用，探究颗粒在真空压力下的迁移规律，未对重力影响进行分析。接触模型采用线性模型，数值模拟材料参数如表2所示。

表2 数值模拟材料参数Tab.2 Numerical Simulation of Material Parameters

2 数值模拟结果与数据分析

2.1 颗粒分布与移动情况

各组数值模拟试验中不同时刻土颗粒的分布情况与颗粒移动速度变化分别如图2、图3 所示，分别选取计算时步在120 万步、220 万步与最终结束状态进行分析。首先，从土颗粒的分布情况来看，真空预压初期采用低真空度进行的组别其颗粒迁移现象较不明显，这是由于较小的真空压力减缓了土颗粒的迁移现象。其次，从3个时间节点土颗粒的分布情况可知，各组试验组土颗粒在不同真空压力下分别进行了不同程度的迁移，T1 到达最终平稳状态所需的时间最短，但其最终土颗粒分布的间距最大，一方面是因为T1 计算时间步短，另一方面是由于T1 真空预压初期采用高真空度会导致细颗粒迁移，远离排水板侧土体大颗粒间缺乏细颗粒填充，导致颗粒间距较大。

图2 不同时刻土颗粒分布Fig.2 Soil Particle Distribution at Different Times

此外，由图3 也可看出真空预压过程中土颗粒的运动变化规律。由于模型为三维模型，故需要对模型进行切片处理，使之转化为二维图片，各组长方体模型均沿模型宽度中心进行切片，图中黑色颗粒部分代表颗粒移动速度缓慢，白色部分代表颗粒移动速度较快。在120 万步时，T1 中靠近排水板处的土颗粒移动速度普遍较低，这是由于在高真空压力下颗粒间移动速度较快，在120万步时颗粒之间已相互接触，颗粒间发生碰撞与挤压，导致移动速度变缓；而其余组别颗粒间距仍较大，在移动过程中颗粒挤压现象不明显，故还具有较大的移动速度。随着计算时步的增加，各组靠近排水板处的土颗粒移动速度都有不同程度减小，其中真空度越高，移动速度缓慢的土颗粒数量越多。

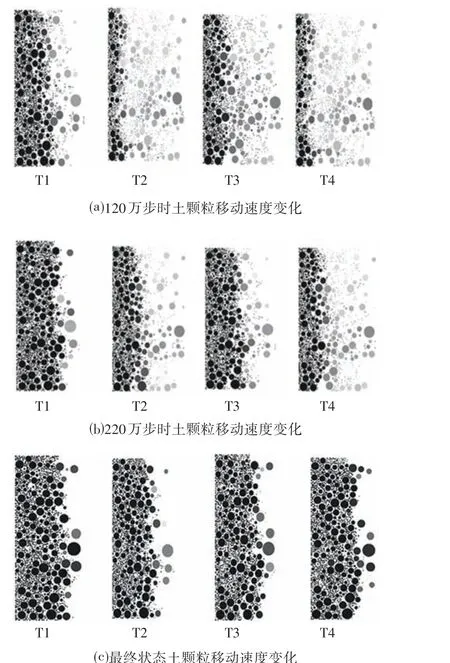
图3 不同时刻土颗粒移动速度变化Fig.3 Variation of Soil Particle Movement Velocity at Different Times

最后，在最终状态时各组土颗粒均已完成迁移并趋于稳定，其中采用分级真空压力的试验组在真空预压初期颗粒迁移速度缓慢，导致靠近排水板处土颗粒较少，有助于减缓淤堵层的形成，而初期采用高真空度的T1 试验组淤堵层形成时间较早，故分级真空预压处理疏浚淤泥时，用排水通道的畅通来增加排水效果［14］。

2.2 靠近排水板处土体孔隙率变化

靠近排水板处测量圆监测到的土体孔隙率变化曲线如图4 所示。通过研究土体孔隙率的变化，可以间接反映真空预压过程中土体渗透路径的大小与长短变化。土体孔隙率大，说明土体中渗透路径宽大，真空预压排水通道畅通，反之孔隙率较小时，说明土体中渗透路径短小，土中水分排出困难。首先，各组模拟试验初始孔隙率均靠近土体整体孔隙率0.7，这是由于土体颗粒分布不均匀，局部孔隙率与土体整体孔隙率接近但有微小偏差，且测量圆的半径也对孔隙率的监测偏差存在一定影响，测量圆半径越大则与土体实际孔隙率越接近。

图4 靠近排水板处孔隙率变化曲线Fig.4 Porosity Curve near Drainage Plate

其次，各组孔隙率在真空压力作用下都逐渐下降，且计算步长为300万步时都趋于稳定，且各组孔隙率在前期下降速度较快而后期下降速度变缓，这是因为模型中颗粒之间存在一定距离，前期在真空压力作用下颗粒相互靠近，导致孔隙率下降速度较快；而后期颗粒间相互接触与碰撞，颗粒之间在移动的过程中寻找接触更为紧密的方式，故孔隙率下降速度缓慢并最终趋于稳定。

此外，与靠近排水板处孔隙变化规律相似，孔隙率在前期下降速度较快，后期速度变缓，且与排水板距离越近，其孔隙率衰减的时间越早，这是由于靠近排水板处真空度大。最后，通过对比各组模拟组别孔隙率下降趋势来看，采用分级真空预压的孔隙率下降速度缓于常规真空预压，而采用三级真空压力加载方式的T4 其孔隙率下降最缓，说明分级真空预压中排水通道畅通时间更久，能有效缓解淤堵层形成，且分三级施加优于二级施加的方式。

2.3 靠近筒壁处土体孔隙率变化

靠近筒壁处测量圆监测到的土体孔隙率变化曲线如图5 所示。首先，各组试验孔隙率在整体趋势都呈现为减小的趋势，但在真空预压初期孔隙率存在先减小后增大的现象。这是由于真空预压前期靠近排水板的土体率先向土体运动，随后真空压力向远离排水板位置处传递，伴随着远处颗粒逐渐向排水板处移动，真空预压前期测量圆内颗粒整体移动速度较缓，等测量圆左侧靠近排水板处的土颗粒完成迁移后会导致测量圆内土体颗粒速度加快，颗粒移动出测量圆的颗粒数目大于进入测量圆内的颗粒数目，故会导致土样孔隙率增大现象。其次，由于前期采用低真空度的T2～T4，其靠近筒壁处孔隙率趋于稳定所需时间较长，但最终孔隙率各组相差不大，这说明采用分级施加真空压力的方式，对土体中最终的孔隙率造成的差异较小，但若处理相同时间，分级真空预压的孔隙率大于常规真空预压，说明分级真空预压有助于减缓淤堵层形成，这与试验得到的结果一致［15］。

图5 靠近筒壁处孔隙率变化曲线Fig.5 Porosity Curve near the Wall of the Cylinder

此外，各组模拟试验的土体孔隙率大幅度减少均发生在真空预压处理前期，而后期孔隙率下降幅度较不明显。最后，T1试验组由于全程采用80 kPa的真空压力进行处理，故其孔隙率下降速度最快，且其到达平稳的状态也最早，说明靠近排水板处土体颗粒接触更为紧密，从而导致淤堵层形成。相对而言，采用分级真空预压的T2～T4则能减缓淤堵层的形成。

2.4 靠近排水板处黏粒含量变化

靠近排水板处测量圆监测到的土体黏粒含量变化曲线如图6所示。通过监测土体不同位置处黏粒含量的变化，可以获得真空预压中细颗粒的迁移规律，以此探究真空预压过程中淤堵层的形成机理。首先，由于模型整体黏粒含量设置为35%，而测量圆内所测得的初始黏粒含量为32.5%，这是因为测量圆只监测模型局部的黏粒含量，而黏粒与粉粒在模型整体分布不均匀，故初始黏粒含量有一定偏差，但在合理范围之内。其次，在计算步长为120万步之内，黏粒含量有较大幅度的变化，这是由于模型生成的颗粒之间间距较大，在真空压力作用下颗粒向排水板处迁移，导致测量圆内颗粒数目增多，故黏粒含量变化较为显著。

图6 靠近排水板处黏粒含量变化曲线Fig.6 The Variation Urve of Clay Content near the Drainage Plate

此外，随着计算步长的增加，黏粒含量趋于稳定，其中T1 最快达到稳定，且在120 万步时T1 组别的黏粒含量最高，说明高真空压力有助于细颗粒的迁移，且在真空压力处理过程初期就已经完成大部分细颗粒的迁移；相对而言采用分级真空预压的T2～T4 黏粒含量分别有略微增加，其中采用20 kPa 的T2 和T4 在120 万步时黏粒含量为33.1%，小于T1 黏粒含量的36.6%。

最后，对比各组真空预压结束时黏粒含量可知，采用分级真空预压的T2～T4 中黏粒含量分别为36%，36.6%和34%，均低于T1 的38.9%。这说明分级真空预压能缓解土体中细颗粒的迁移，其中分三级施加真空压力的方式能最大程度上降低细颗粒迁移数量，有助于缓解淤堵层的形成。

2.5 靠近筒壁处黏粒含量变化

靠近筒壁处测量圆监测到的土体黏粒含量变化曲线如图7 所示。首先，真空预压初期黏粒含量的波动幅度较大，这与靠近排水板处的黏粒含量变化的原因相同。其次，各组黏粒含量在初期波动后都有一个明显的陡降和小幅度上升变化的过程，这是由于测量圆左侧土体已经向排水板迁移完成，导致测量圆内颗粒迁移速度加大，故短时间内黏粒含量发生显著降低；但由于测量圆内土体发生迁移后，测量圆右侧远离排水板的颗粒也开始加速向排水板移动，导致测量圆内细颗粒数目又有一定补充，所以黏粒含量存在这一先陡降后上升的现象。

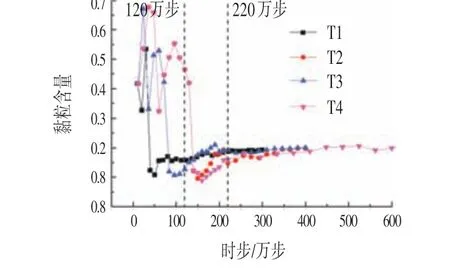
图7 靠近筒壁处黏粒含量变化曲线Fig.7 The Variation Curve of Clay Content near the Wall of the Cylinder

此外，真空预压初期采用低真空度的组别，该现象发生的越迟，其中T2 与T4 都在120 万步后增大真空压力才出现先陡降后上升的过程，而在20 kPa 压力下都只在一定范围内的波动，说明20 kPa 能使土体中大颗粒与细颗粒整体向排水板迁移，防止细颗粒在排水板处聚集形成淤堵层或堵塞排水板滤膜上的排水通道，使得真空预压排水效果降低。

最后，通过对比各组真空预压结束后黏粒含量可知，各组最终的黏粒含量相差不大，黏粒含量都在20%左右，且都低于初始黏粒含量与靠近排水板处黏粒含量。这说明真空预压中远离排水板处的细颗粒存在向排水板处迁移的现象，但分级真空预压与常规真空预压对在排水板与筒壁中间部分土体细颗粒含量的基本无差异影响，而对靠近排水板处黏粒含量影响显著，这可能是由于中间部分土体细颗粒的迁出会伴随着靠近筒壁处细颗粒的迁入。

3 结论

本文针对分级真空预压法处理疏浚淤泥的过程进行离散元模拟分析，根据数值模拟结果及数据分析，得出以下结论：

⑴ 真空预压初期采用高真空度会加快颗粒迁移，到达最终平稳状态所需时间更短，加快淤堵层的形成，降低了真空预压处理效果。

⑵真空预压前期采用高真空度会导致土体孔隙率下降速度加快，而分级真空预压能减缓排水板附近孔隙率下降速度，其中分三级的分级真空预压孔隙率下降速度最缓慢，说明分级真空预压能减缓排水板附近的淤堵层形成，土体排水通道畅通，提高土体排水效率。

⑶真空预压过程中存在颗粒迁移现象，其中远离排水板的细颗粒会在真空预压作用下向排水板迁移使得排水板处细颗粒含量增加，从而产生致密的淤堵层，而分级真空预压前期采用低真空度的方式能减少细颗粒的迁移，减缓排水板处淤堵层形成。