双离合器协同的功率分流式混合动力汽车动态协调优化控制研究*

施德华，容香伟，汪少华，张开美，陈 龙，李 春

（1.江苏大学汽车工程研究院，镇江 212013；2.汽车零部件先进制造技术教育部重点实验室（重庆理工大学），重庆 400054；3.金龙联合汽车工业（苏州）有限公司，苏州 215026）

前言

《节能与新能源汽车技术路线图2.0》中明确提出要大力发展混合动力技术，其中高集成度、高性能的功率分流式混合动力汽车（hybrid electric vehicle，HEV）更是研究的热点［1］。面对结构更智能的动力耦合装置的需求，国内外科研机构和整车企业相继推出了集成多离合器的功率分流式动力耦合装置［2］，但复杂的多离合器构型对HEV瞬态模式切换的动态协调控制带来了更大挑战，影响驾驶平顺性。

为改善HEV由纯电动切换至混合动力模式时伴随发动机起动及离合器状态切换对行驶平顺性造成的不利影响，国内外研究学者基于模型预测控制、滑模控制和动态规划等算法对发动机起动转速进行优化［3-5］，以提高发动机起动阶段或离合器状态变化时的切换品质，但这些控制策略计算量大、实际应用较为复杂。针对发动机起动需求，Chen等［6］基于功率分流式传动系统的耦合特性设计了前馈-反馈控制器。Chen等［7］设计一款连接发动机与变速器的新型阻尼离合器，并根据行星排传动系统的耦合特性研究了发动机起停过程降低转矩波动的方法。汪佳佳等［8］针对一款功率分流式传动系统提出基于电机补偿的协调控制方法。同时，为解决模式切换过程中离合器状态切换的问题，Yang等［9］基于一款同轴并联混合动力客车，将切换过程划分为5个子阶段并基于H∞鲁棒控制设计动态协调控制器。秦大同等［10］结合二次型最优控制研究AMT与DCT离合器的起步与换挡过程。Zhu等［11］根据离合器和发动机的工作状态将模式切换过程划分多个子阶段，采用模糊PID控制设计转矩反馈补偿器降低切换冲击，并通过最优控制改善了离合器滑摩损失。然而，上述控制方法的设计仅针对单离合器的传动系统，鲜有研究双离合器协作下伴随发动机起动过程的模式切换。

针对集成多离合器的功率分流式混合动力系统，通过控制不同离合器的工作状态组合可以实现更丰富的工作模式，扩大动力源经济工作区间，但在进行模式切换时，往往伴随两个离合器工作状态的协同变化（超过两个离合器协同的复杂情况应避免）［12］，而不同离合器滑摩时的功率分流式传动系统不仅自由度增加，耦合效果减弱，而且随着发动机起动、离合器工作的非连续性进一步导致控制变量增多，协同状态发生迁移，在面对不同加速工况时，对动力源输出转矩分配更加敏感，极容易引起总输出转矩的波动，造成瞬态模式切换品质的下降。

本文中以一款集成多离合器的功率分流式HEV为对象，开展包含两个离合器状态协同切换的纯电动模式到混合动力模式的动态协调优化控制策略研究。通过分析其瞬态模式切换行为，确定各个切换阶段不同动力源及离合器动态协调控制方法，在此基础上，基于模拟退火算法优化双离合器的协同滑摩行为，并提出面向不同加速工况的发动机转速自适应调节策略，通过电机MG1输出转矩的自适应调节提高大范围运行工况下的整车瞬态模式切换品质，为集成多离合器的功率分流式HEV动态协调控制提供一种新的思路。

1 功率分流式混合动力汽车建模

1.1 模式切换动力学模型

所研究的功率分流式HEV构型如图1所示，集成4个离合器的双行星排构型实现发动机、电机MG1和MG2输出动力的耦合。即发动机与前行星排PG1的齿圈R1相连，前行星排的行星架C1分别接有离合器CR3和CR1，电机MG1和MG2分别与PG1的太阳轮S1和后行星排PG2的太阳轮S2相连，PG2的齿圈R2通过离合器CR2与PG1的 太 阳轮S1相连，PG2的行星架C2连接离合器CR1和输出轴。

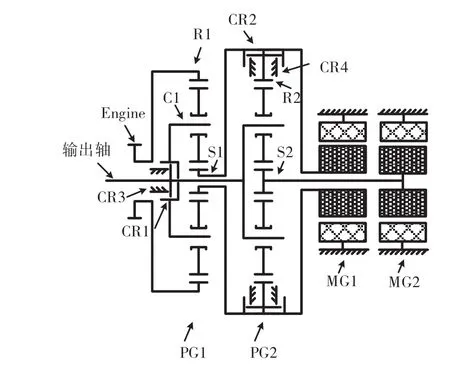
图1 混合动力构型

该构型模式切换常涉及双离合器的协同工作，本文中以如图2所示的纯电动模式到混合动力模式的瞬态切换过程为研究对象，该切换过程具有典型性，不仅包含两个离合器的协同作用，还涉及发动机起动过程。针对瞬态模式切换过程，基于杠杆法和矩阵法建立动力学模型［13］，以CR1和CR3同时滑摩的阶段为例，建立图3所示的双行星排杠杆模型。

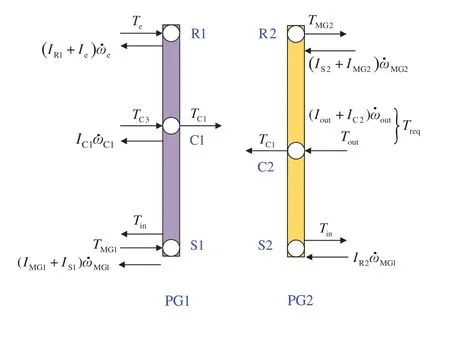
图3 双行星排杠杆模型

根据图3所示的杠杆模型，进一步通过矩阵的形式描述其动力学方程，如式（1）所示。

同理，建立纯电动模式和混合动力模式的传动系统动力学矩阵方程，如式（2）和式（3）所示。

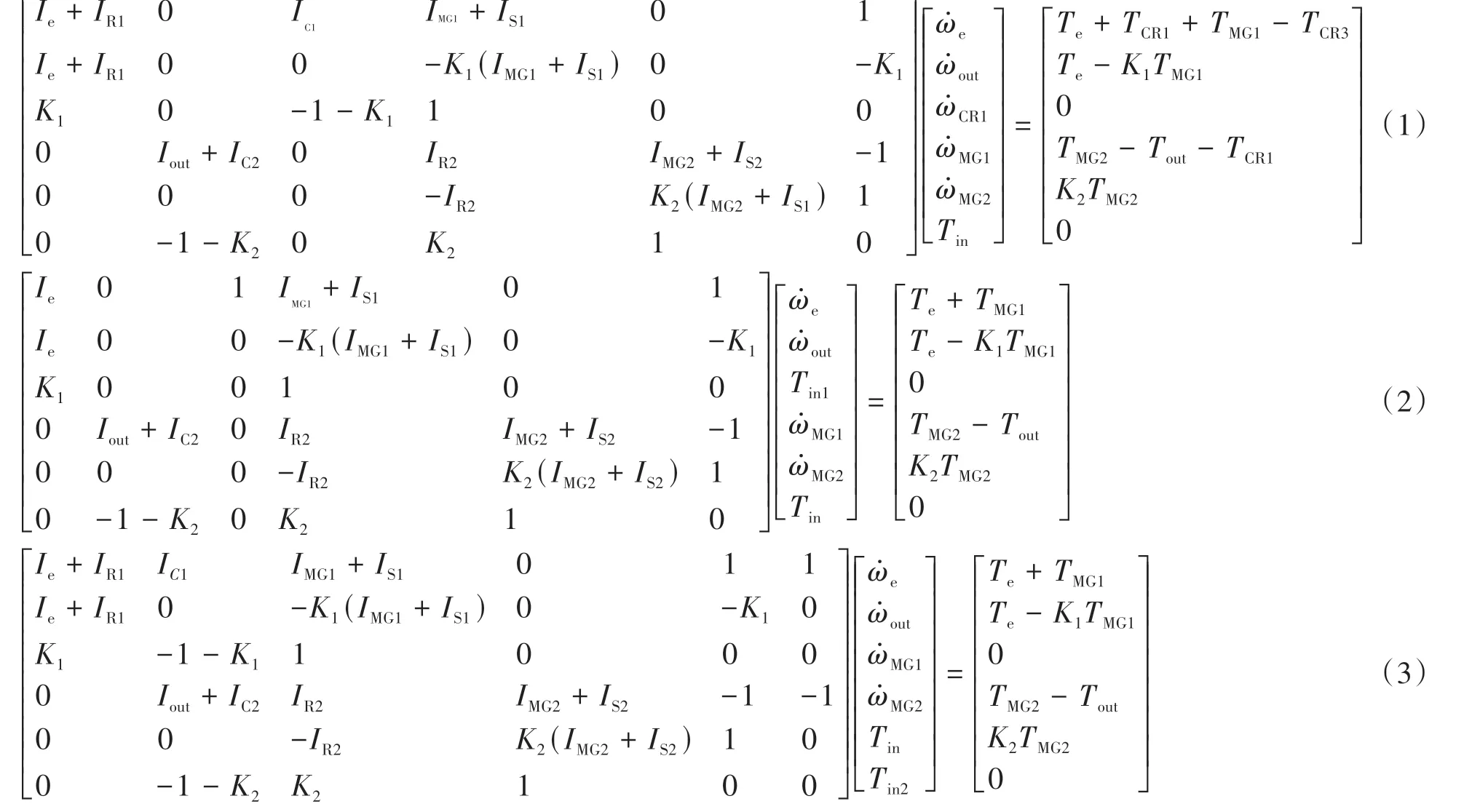
式中：Ie、IR1、IMG1、IS1、IMG2、IR2和Iout分别为发动机、R1、MG1、S1、MG2、R2以及输出轴的转动惯量；IC1、IC2分别表示为离合器CR3与行星架C1的转动惯量之和、离合器CR1与行星架C2的转动惯量之和；ωe、ωC1、ωout、ωMG1、ωMG2分别为发动机、C1、输出轴、MG1以及MG2的转速；Te、TMG1、TMG2、TCR1和TCR3分别为发动机、MG1、MG2、CR1以及CR3传递的摩擦转矩；K1、K2为行星轮系特征参数，且K1=K2；Tin为S1与R2连接间的内力矩；Tin1为CR3锁止的内力矩；Tin2为行星架C1与C2之间的内力矩；Tout为输出轴负载转矩。Tout可由汽车平衡力矩方程计算：

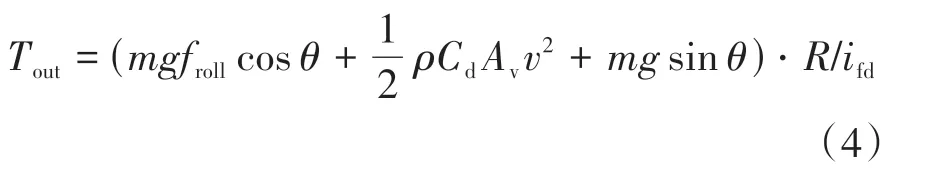
式中：m为整车质量；g为重力加速度；θ为坡度角；froll为滚动阻力系数；ρ为空气密度；Cd为空气阻力系数；Av为迎风面积；v为车速；R为车轮半径；ifd为主减速器传动比。

整车模型参数如表1所示。

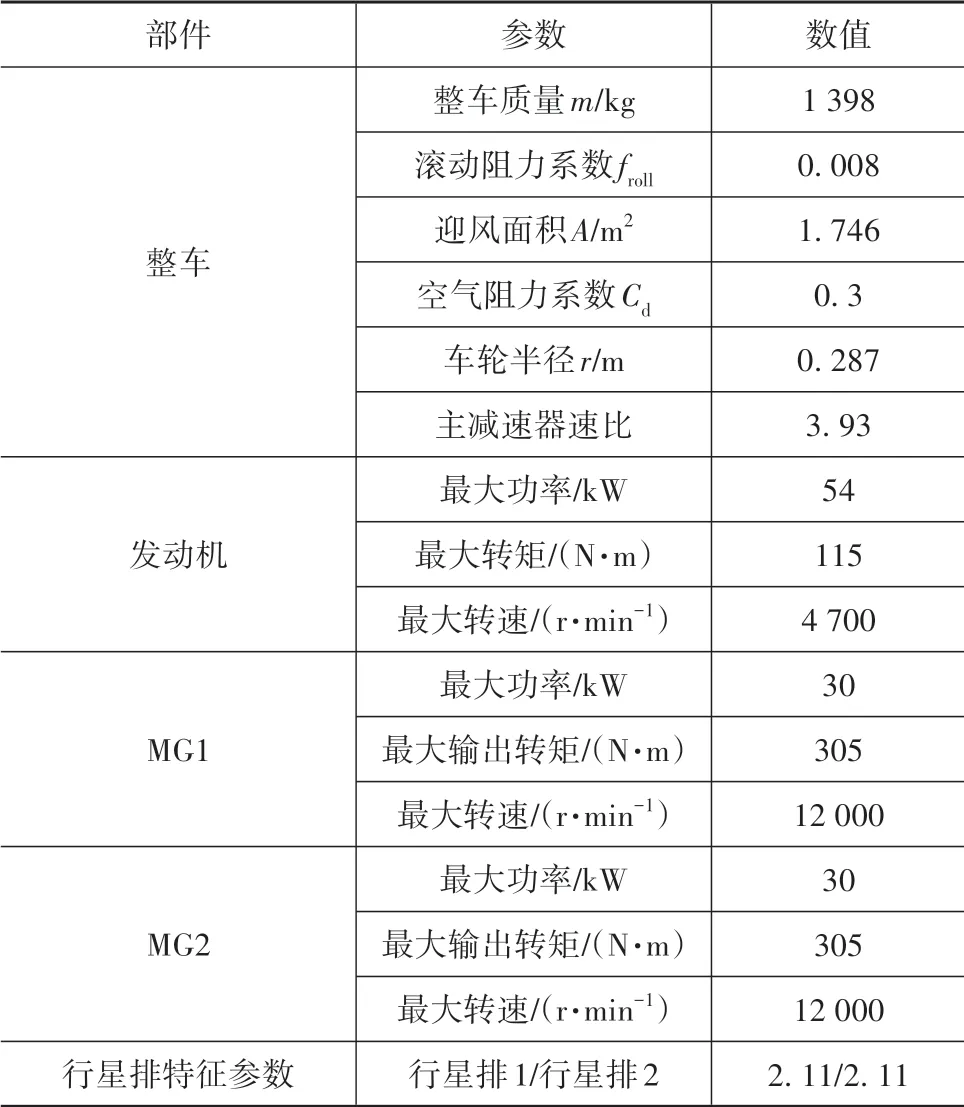
表1 整车模型参数

1.2 关键零部件建模

（1）发动机和电机模型

本文采用“1阶惯性延迟环节”描述发动机和电机的瞬态转矩输出模型［14］，发动机和电机输出转矩定义为

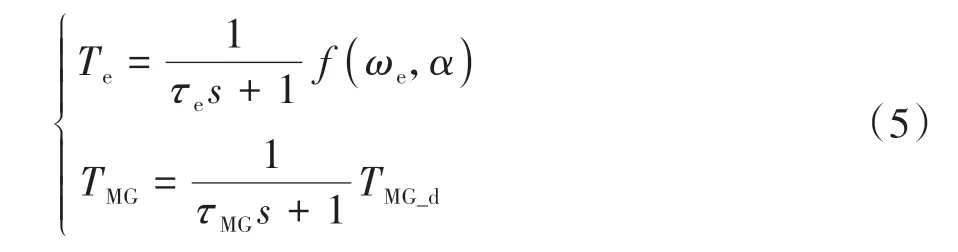
式中：α为节气门开度；ωe为发动机转速；τe、τMG1分别表示发动机和电机的动态响应时间，且τMG1远小于τe；TMG_d为电机目标转矩。

（2）离合器模型

国外大量离合器油压试验表明离合器接合过程及分离过程滑摩时的油压曲线可描述为指数函数形式［15］，进而结合湿式离合器摩擦转矩表现形式［16］，离合器接合和分离过程的摩擦力矩可表示为

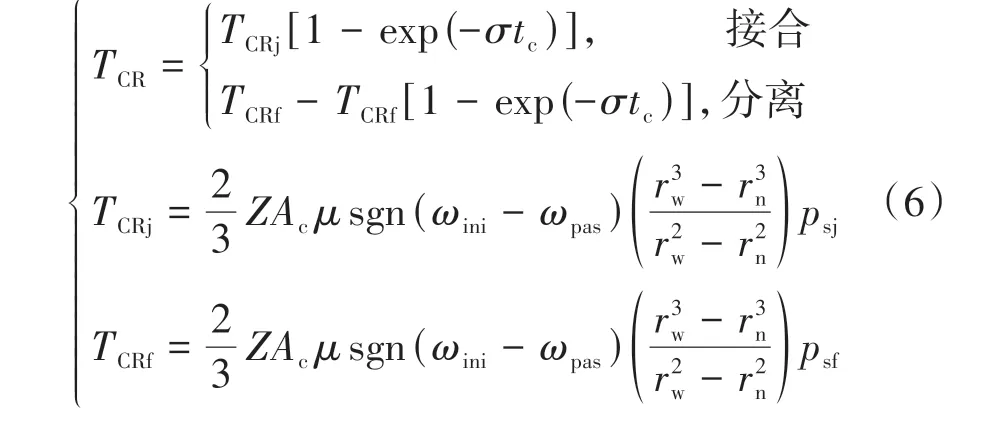
式中：σ为油路充油速度相关的系数；tc为接合或者分离所用的时间；TCRj和TCRf分别定义为离合器接合目标转矩、刚分离时转矩；ωini、ωpas分别为离合器主、从动片转速；μ为离合器摩擦因数；psj、psf分别为离合器结合与分离时的主油道油压；Z为摩擦片个数；Ac为摩擦片面积；rw、rn分别为摩擦片外、内径。研究中不考虑离合器摩擦因数μ的变化特性。

2 动态协调优化控制策略

2.1 双离合器协同的模式切换行为分析

综合考虑模式切换品质及发动机起动需求，在纯电动模式，通过MG1将发动机调速至600 r/min以避免发动机在模式切换阶段中因转速耦合被反拖，并减少发动机到达怠速转速（900 r/min）的时间。在发动机和双电机联合驱动的混合驱动模式阶段，通过电机调速使发动机工作于经济转速区间。瞬态模式切换过程涉及两个离合器的协同工作：CR3由锁止经滑摩到分离，CR1则由分离趋向锁止。

CR1和CR3的工作时序存在着丰富的组合方式，须结合发动机的起动需求进行切换可行性分析。因此，假设存在图4中所示的4类双离合器协同切换序列。

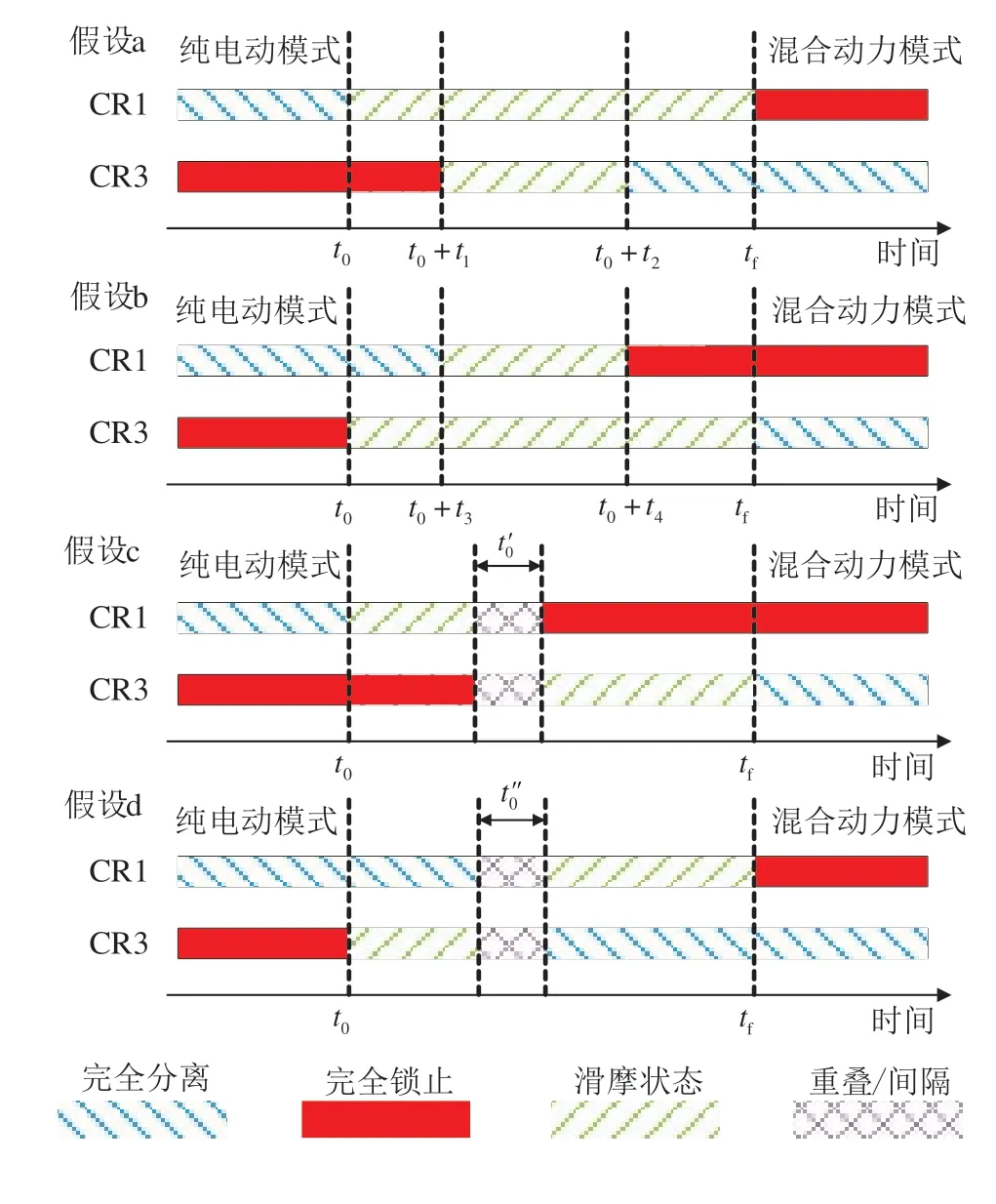
图4 工作时序

假设a：CR3在CR1工作过程中分离（t0+t1、t0+t2表示CR3分离开始、结束时刻）。

假设b：CR1在CR3工作过程中结合（t0+t3、t0+t4表示CR1接合开始、结束时刻）。

假设c：CR1先结合、先锁止，CR3后滑摩、后分离（t′1为CR3与CR1工作重合或间隔时间）。

假设d：CR3先滑摩、先分离，CR1后结合、后锁止（t″0为CR3与CR1工作重合或间隔时间）。

其中，t1、t2、t3、t4分别为［0，（tf-t0）/2］内的值；当为重叠时间时当为间隔时间时

由式（6）可知，当离合器主、从动盘转速差为正时，离合器摩擦转矩为正，反之为负。假设b中，CR3先滑摩传递给行星架C1负摩擦转矩，降低C1角加速度。虽然CR1滑摩会给C1传递正摩擦转矩，但若CR3滑摩时间长于CR1滑摩时间，行星架C1的转速很难与输出轴转速同步，难以完成模式切换，导致离合器无效工作。而假设a的CR3工作时间小于CR1，更容易缩小行星架C1与输出轴转速差，完成模式切换。同理，在假设c和d中，当CR1工作时间小于CR3时，很难迫使C1和输出轴转速同步；而在假设c和d中，当CR3工作时间小于CR1时，从切换时间角度来看，同等工作条件下的假设c和d切换时间要长于假设a，故综合考虑切换时间和离合器的工作有效性，选择假设a作为双离合器工作时序。

在假设a的基础上，可以通过控制t1、t2细分为更多的工作时序，但进一步考虑到双离合器控制难度，选择双离合器同时分离、锁止的时序最为简单适宜，便于后续控制策略设计。结合纯电动切换至混合驱动模式中发动机起动及CR1两端转速差的控制需求，可设计如图5所示的模式切换逻辑。其中，vthr为切换速度阈值，取5.5 m/s。

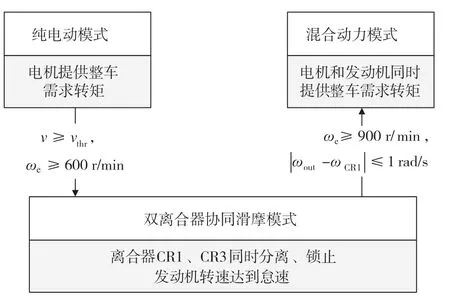
图5 模式切换逻辑图

2.2 动态协调控制策略设计

为了改善不同加速工况下的功率分流式HEV模式切换品质，根据系统稳态转矩分配、驱动轴动态加速以及发动机转速调速等需求，建立各切换阶段不同动力源转矩分配策略。

2.2.1 纯电动模式

纯电动模式下两电机均参与工作，针对系统的2自由度特征，采用PI转速调节模块由MG1调节发动机转速，使发动机工作在目标转速。根据行星排动力耦合机构转矩平衡表达式并结合PI调速模块对电机进行转矩分配：

式中TPI1为纯电动模式下PI转速调节模块的需求转矩，具体表示为

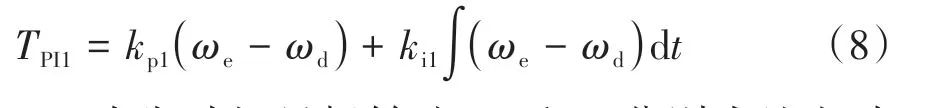
式中：ωd为发动机目标转速；kp1和ki1分别为纯电动模式下PI调节模块的比例、积分增益；Treq为输出轴需求转矩。Treq可基于结合汽车动力学平衡方程和PI控制的驾驶员模型求解，记为

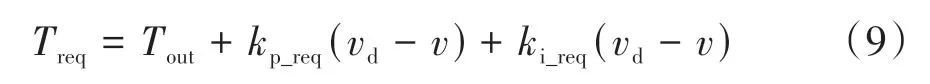
式中：kp_req和ki_req分别为PI控制模型的比例和积分增益；vd为目标车速。

该模式系统冲击度表示为

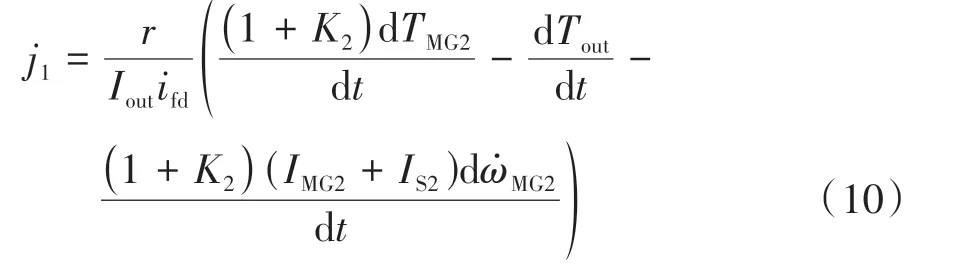
由式（10）可以看出，该模式系统冲击度受到TMG2、Tout以及MG2加减速行为的影响。由于S1与R2相连，MG2与MG1的转速成比例关系，又由于CR1锁止，发动机与MG1转速也成比例关系，因此，整车冲击还将受到MG1对发动机PI调速功能的影响。当该模式切换到下一模式前，发动机转速已达到目标转速，纯电动模式的PI调速模块输出转矩经过较长时间已经趋于稳定，发动机转速也趋于稳定，进而MG2转速也趋于稳定，转矩分配更多地表现为准稳态特性。在模式切换的瞬态过程，车速和加速度视为恒定，根据系统的转速耦合行为和准稳态转矩分配特性，系统模式冲击度也几乎为零。

2.2.2 双离合器协同滑摩模式

该模式下CR1和CR3同时处于滑摩状态，不同于前述纯电动模式后期的准稳态行为，该瞬态切换阶段离合器因滑摩传递输出转矩且各动力源转速持续变化，系统冲击度表示为

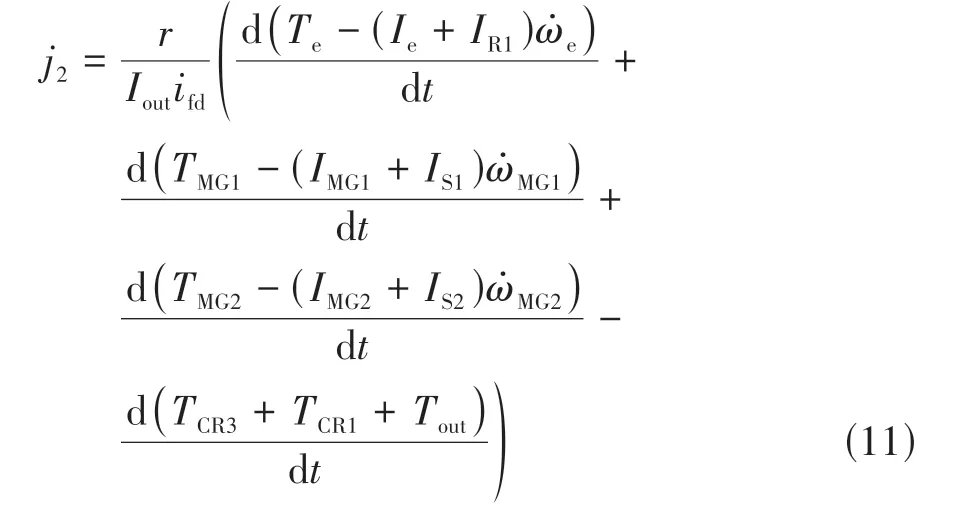
可以看出，该切换阶段系统冲击度将受到各动力源输出转矩以及不同行星排构件转速（各动力源转速）变化的影响。此时，由于瞬态切换车速变化不大，Tout可视为定值，而CR1和CR3均处于滑摩状态，CR1和CR3传递的滑摩转矩持续变化，如式（12）所示，仅按照能量管理策略的各动力源准稳态转矩分配将导致驱动轴实际输出转矩与需求转矩的失配，不同行星排构件转速（各动力源转速）持续变化。因此，为了减小输出轴的转矩波动，电机不仅需要提供目标车速和加速度下的驱动轴需求转矩，还需要补偿发动机的起动阻力矩和动力源加减速行为带来的转矩波动。进一步仍需协调离合器滑摩转矩，发动机转速可由离合器传递的摩擦转矩提升至怠速。为此，设计如式（13）所示的MG1和MG2输出转矩动态协调控制律。

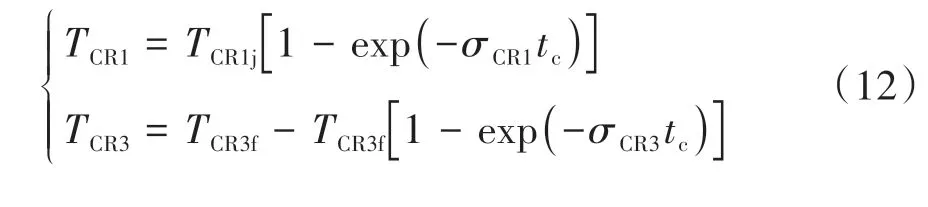
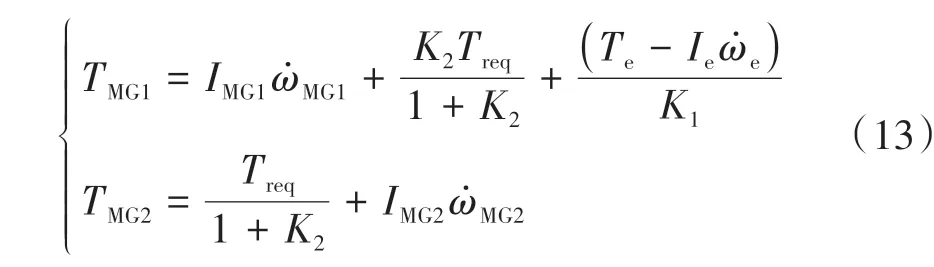
式中：σCR1和σCR3分别为CR1与CR3油路充油速度相关的系数；TCR1j为CR1接合时目标转矩；TCR3f为CR3刚分离时转矩，根据稳态转矩方程可得TCR3f=（K1+1）Te；Te为起动阻力矩，同样可根据发动机起动阻力数据通过BP神经网络进行训练预测。

CR1和CR3传递的摩擦转矩是造成该阶段各部件加减速和输出轴转矩波动的重要因素，为进一步减小由双离合器协同滑摩造成的影响，通过优化CR1和CR3摩擦转矩以提高该切换阶段的瞬态工作品质。基于表征模式切换品质的冲击度、滑摩功及切换时间3个指标建立加权优化目标，分别对CR1的接合目标转矩TCR1j以及CR1与CR3油路充油速度相关的系数σCR1和σCR3进行参数优化，其中，离合器CR1的目标转矩TCR1j仅需优化接合时主油路油压ps即可，具体优化模型描述为

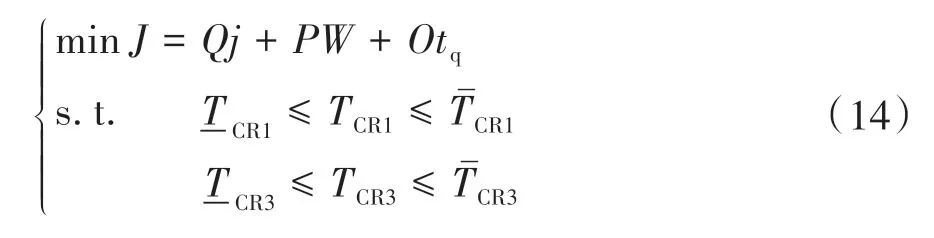
式中Q、P和O分别为冲击度、滑摩功和切换时间的权重系数。

模拟退火算法能够处理不同类型的优化设计变量，具有较强的全局收敛性和广泛的自适应性［17］，这种算法基于Metropolis准则重复进行“产生新解-计算目标函数误差-接受（舍弃）新解”，通过控制温度T使得固体内能E趋于最佳平衡状态，通常表示为

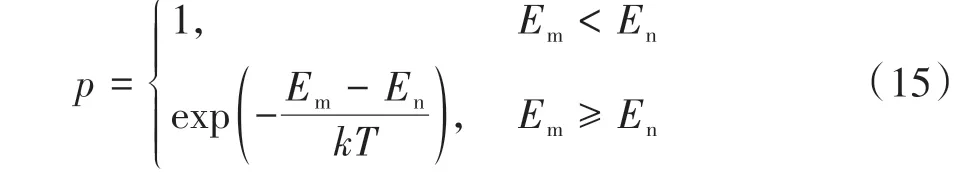
式中：p为出现能量差为dE的降温的概率；Em、En分别表示为新、旧时刻固体内能；T为固体温度；k为常数。

本文中结合模拟退火算法将离合器动作参数TCR1j、σCR1和σCR3当做算法的解，通过逐步降温并添加随机干扰得到最优的目标函数值。将离合器传递转矩限制在物理约束内，当其参数变化后得到的Jm小于Jn时，则接受该次变化，当参数变化后的Jm大于Jn时，则以一定概率继续移动且此概率随着时间而衰减。

2.2.3 混合动力模式

（1）切换冲击机理分析

该阶段CR1和CR2处于锁止状态，CR3和CR4分离，发动机参与驱动，双行星排动力耦合机构具有2自由度，在根据能量管理策略确定各动力源稳态转矩分配的基础上，分别对MG1和MG2增加基于PI控制的动态转矩调节模块，由MG1和MG2调节发动机转速，使发动机工作在目标转速。MG1和MG2输出转矩为

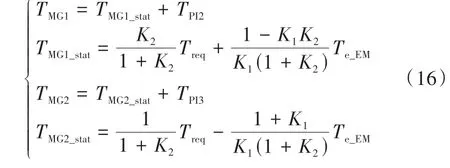
式中：TMG1_stat和TMG2_stat分别为MG1和MG2根据能量管理策略得到的稳态输出转矩；TPI2和TPI3分别为混合动力模式下基于PI控制的MG1和MG2动态调节转矩，PI转速调节模块的输入均为发动机理想转速与实际转速的差值。

混合动力模式下，输出轴冲击度为

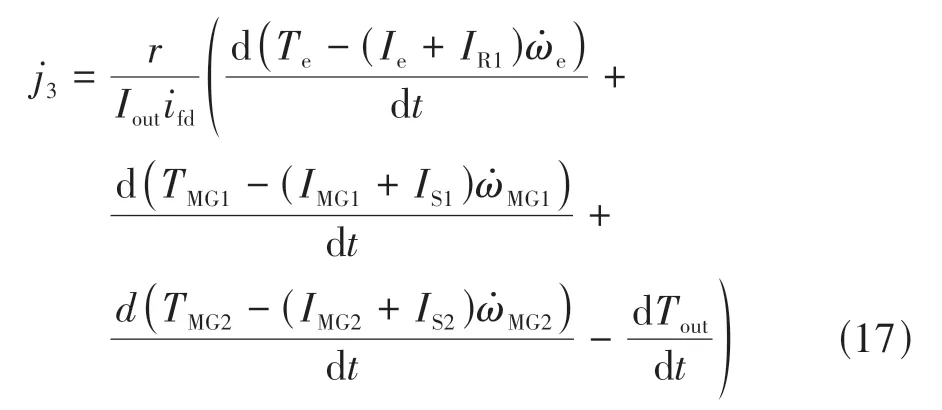
双离合器协同滑摩阶段切换到混合动力模式的初始阶段，发动机转速仍未达到目标转速，阶跃式的发动机转速跟踪使式（16）中MG1和MG2提供较大的动态调节转矩，即TPI2和TPI3均不为零，由于行星排转速耦合关系，发动机转速动态调节也使MG1和MG2转速随之时变。另一方面，在该模式初始阶段，发动机输出转矩由于响应迟滞尚未达到能量管理策略确定的稳态输出转矩，即dTe/dt不为零。因此，结合式（16）可知，该模式初始阶段产生的冲击不仅受到MG1和MG2对动力耦合机构调速功能的影响，也受到发动机响应迟滞特性的影响。

（2）自适应动态协调控制策略

针对发动机响应迟滞以及MG1和MG2调速导致的模式切换冲击，构建如图6所示的混合动力模式各动力源协调控制策略。在结合能量管理策略转矩分配［18］以及PI控制的转速调节的基础上，针对MG1设计自适应调节系数实现不同加速工况下的MG1输出转矩自适应调节，MG2输出转矩还需要提供额外的补偿转矩TMG2_com以弥补由于发动机响应迟滞导致的发动机实际输出转矩与理想转矩的差异。发动机转矩控制指令Te_EM由能量管理策略给定，本文中主要研究瞬态模式切换行为，稳态能量管理策略在此不再赘述［19］。

图6中，发动机响应迟滞补偿转矩可表示为

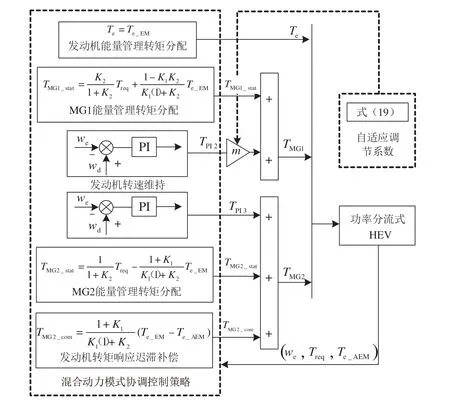
图6 混合动力模式协调控制策略

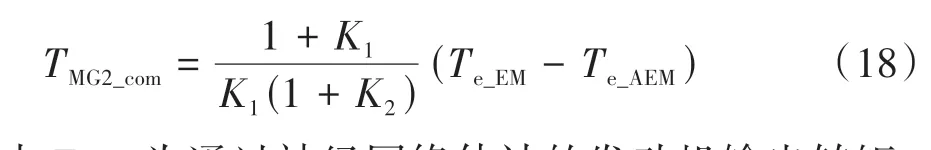
式中Te_AEM为通过神经网络估计的发动机输出转矩，可基于发动机动态响应输出转矩数据通过BP神经网络训练估计得到［20］。

由于驾驶汽车工况的复杂多变性，导致系统在切换至混合动力模式时发动机转速与目标跟踪转速并非定值，因此，固定的调速模块PI参数难以兼顾发动机转速调节性能和输出轴转矩波动的限制。图7对比了加速度分别为2、2.1和2.2 m/s2的不同加速工况下采用固定PI调节系数时的模式切换冲击度。当加速工况为2.2 m/s2时，最大冲击度为23.6 m/s3，超出我国限定的冲击标准（17.64 m/s3），而对于2 m/s2的加速工况，最大冲击度仅为8.8 m/s3，低于德国标准（10 m/s3），不同加速工况系统冲击度差异显著。这主要是因为，加速工况的改变使整车需求转矩发生变化，从切换阶段进入混合动力模式时，固定的PI调节系数使电机根据发动机转速提供固定的调节转矩，不随加速工况改变，因此在混动阶段初始时刻，各动力源转矩经过耦合后难以满足不同加速工况下的转矩需求，降低切换品质。

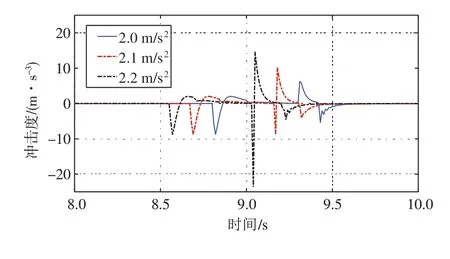
图7 不同加速工况下的冲击度

针对固定PI调节参数无法保证大范围工况下瞬态模式切换的高品质控制，提出MG1对发动机转速的自适应调节方法。由式（16）可知，当不考虑MG1调速时，MG1的输出转矩与总需求转矩Treq成正相关关系。结合式（17）的混合动力模式的冲击机理分析可知，通过保持MG1输出转矩与整车需求转矩成正相关的关系，就能够维持总输出转矩平缓变化。为此，当考虑PI调速时，需要自适应PI调节系数能够随着加速工况的变化不断调节参数使MG1输出转矩与整车需求转矩维持正相关的关系。因此，在某一加速工况下，通过优化选择最优的PI调节参数以兼顾转速调节性能且维持输出转矩平缓波动，并将此时的PI模块的输出转矩与总需求转矩之间的关系作为参考设计能实时调整的自适应调节系数。定义n为PI模块输出转矩与总需求转矩之间的关系，进而根据式（16）反向求解出自适应调节系数μ。

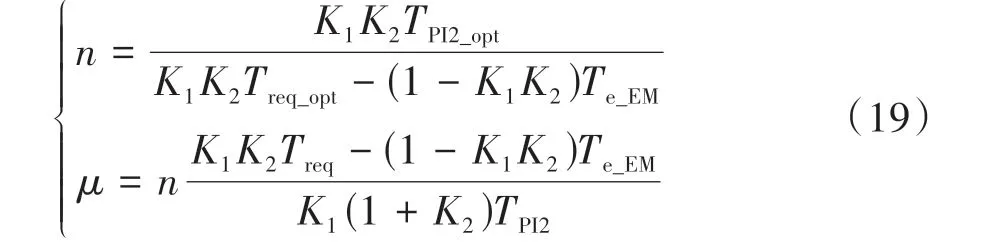
式中：TPI2_opt和Treq_opt均为通过某一工况下优化后得到的值；Te_EM在此瞬态中可视为定值。

结合式（16），混合动力模式下的各动力源输出转矩最终可表示为

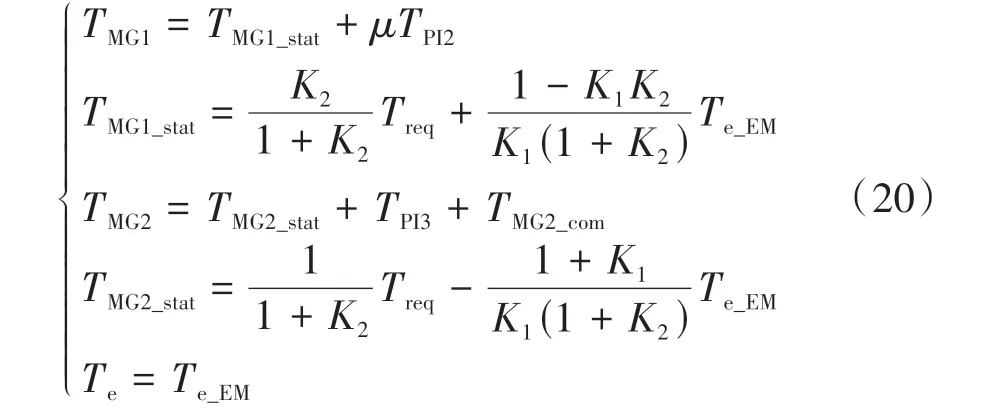
通过引入MG1调速模块的自适应调节系数μ即可实现MG1输出转矩面向不同加速工况的自适应调节，从而在实现发动机目标转速控制的同时保证大范围工况模式切换品质。

3 仿真结果与分析

为验证本文提出的控制策略的有效性，分别对既无离合器滑摩转矩优化也无发动机转速调节自适应的切换策略（策略A）、仅有发动机转速自适应调节（策略B）以及本文提出的动态协调优化策略（策略C）进行对比测试。通过前述动态协调控制方法选取1.8、2.3和2.8 m/s2的加速工况为测试工况，具体仿真参数如表2所示。

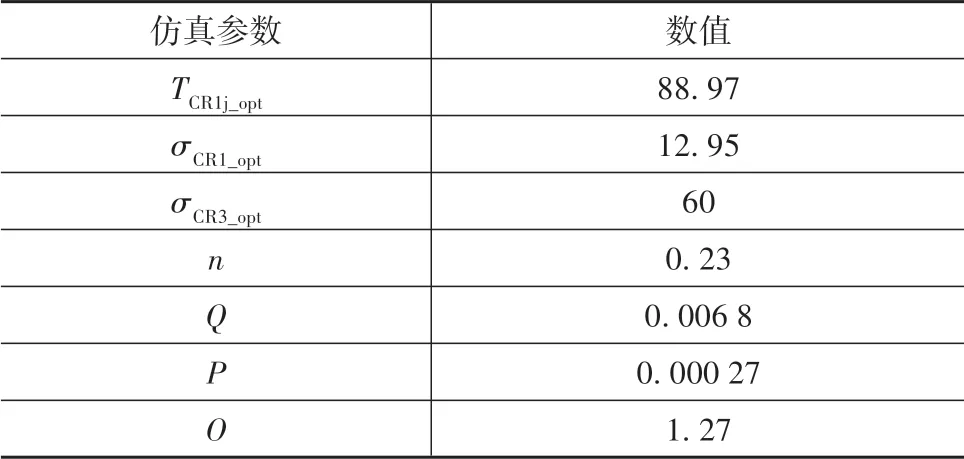
表2 仿真参数

表中：Q、P、O权值可通过权重系数除以基准值得到；冲击度、滑摩功和切换时间的基准值可设计为17.64、2 200和0.55；权 重 系 数 分 别1.2、0.6和0.7。

图8对比了不同控制策略下的模式切换评价指标，包括整车冲击度、离合器滑摩功和模式切换时间。由图8（a）可知，策略A未优化离合器参数，导致在模式切换过程中难以协调整车输出转矩，所产生的冲击度最大绝对值可达15.1 m/s3，策略B未采用本文设计的自适应调节系数，在加速度为2.3 m/s2以上的工况下效果良好，但在1.8 m/s2的加速工况下冲击度达到47.7 m/s3，无法适用于大范围加速工况，而策略C既通过模拟退火优化参数又采用自适应调节系数，其冲击度在不同的加速工况下均能保持在10 m/s3以内。图8（b）和图8（c）表明，策略B、C的滑摩功和切换时间一致，工况的变化仅影响到整车冲击，而且相较于策略A，离合器参数经过模拟退火优化后，降低了离合器的滑摩功和模式切换时间，以1.8 m/s2的工况为例，策略A的滑摩功和切换时间分别为2 411 J、0.59 s，大于策略B、C的2 120 J和0.52 s，分别提升12.1%和11.9%。随着加速工况的变化，切换时间也会随之呈正相关变化，当离合器参数确定后，离合器滑摩产生的能量损失将会随着切换时间降低而减小。

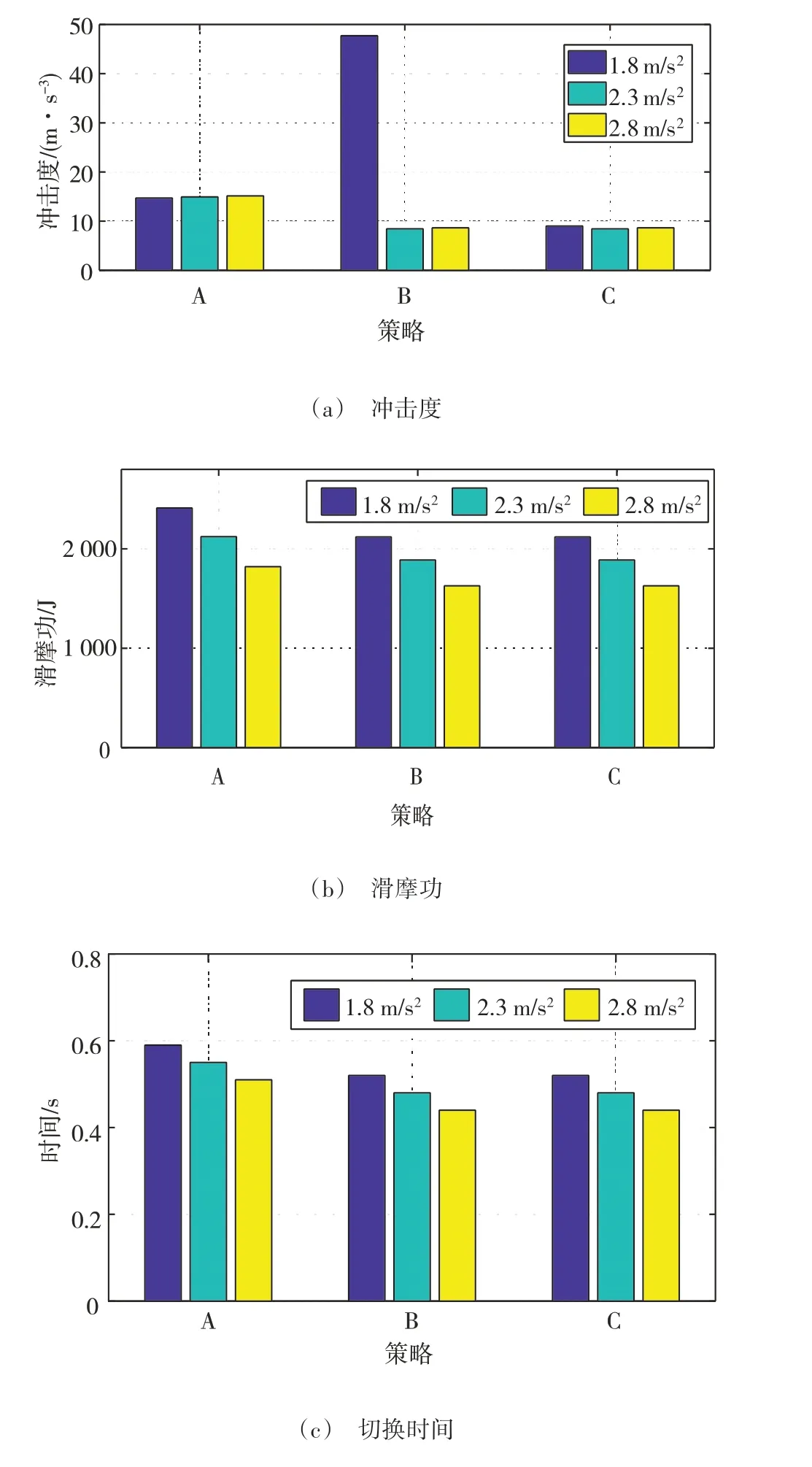
图8 评价指标

通过对比A、B、C 3种策略在不同加速工况下的结果，发现本文设计的动态协调策略C在整个模式切换过程中都能保持良好的切换品质。

图9给出了策略B、C下行星排混合动力系统不同部件转矩和转速的动态响应。由图9（a）可以看出，B、C 2种策略均能够在纯电动模式中将发动机转速维持在600 r/min附近，且可在混动模式下将发动机转速维持在经济转速区间。图9（b）和图9（c）表明在3种不同加速工况下C1与输出轴转速皆有较好同步效果。图9（d）和图9（e）分别为电机MG1与MG2的输出转矩，可以看出，当采用策略B时，在1.8 m/s2加速工况下整车由离合器滑摩阶段切换至混合动力模式的瞬间为9.6-9.7 s，电机MG1为了跟踪发动机的目标转速，产生较大的突变转矩，而采用策略C时，MG1输出转矩更加平缓，2种策略下的MG2输出转矩均比较平缓。

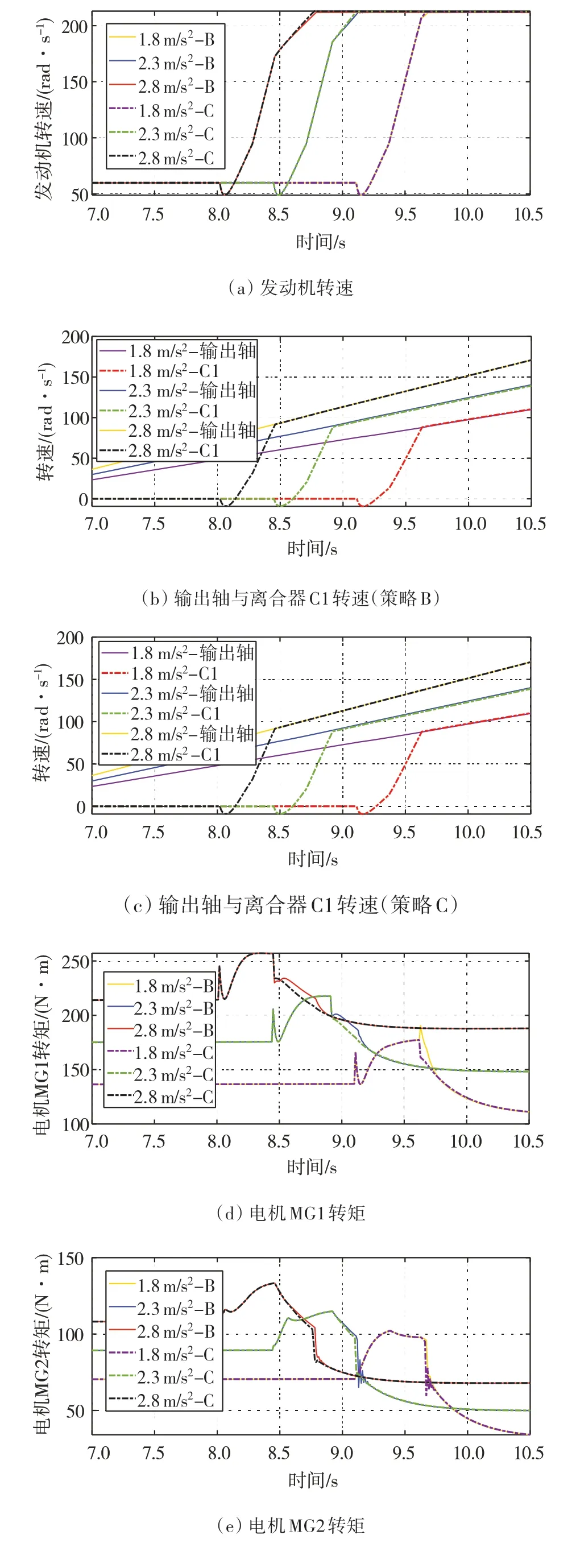
图9 动力源转矩和转速

4 硬件在环测试

通过硬件在环（hardware in the loop，HIL）测试进一步验证本文所提出的控制策略的性能，HIL测试原理如图10所示。HIL测试台主要包含上位机和HCU-HIL机柜，其中机柜主要由快速成型控制器（D2P）、包含各种板卡的NI实时仿真机、信号调理模块、总开关以及可编程电源等部件组成。控制器模型在Motohawk平台进行搭建，并利用Mototune下载至D2P控制器中，被控对象模型编译为dll文件并添加至NI Veristand中，同时添加实时目标机使得上位机IP地址与实时仿真机在同一子网段内，通过数据库CAN接口文件（DBC）进行软硬件I/O口映射，连接控制器与被控对象的输入、输出信号，根据以太网进行通信，实现控制器与被控对象之间的闭环连接，通过Veristand在线显示仿真结果［21］。最后，运行HCU-HIL机柜的总开关，实现NI实时模拟器底层数据到控制器的传输，HIL测试的模型参数与仿真保持一致。

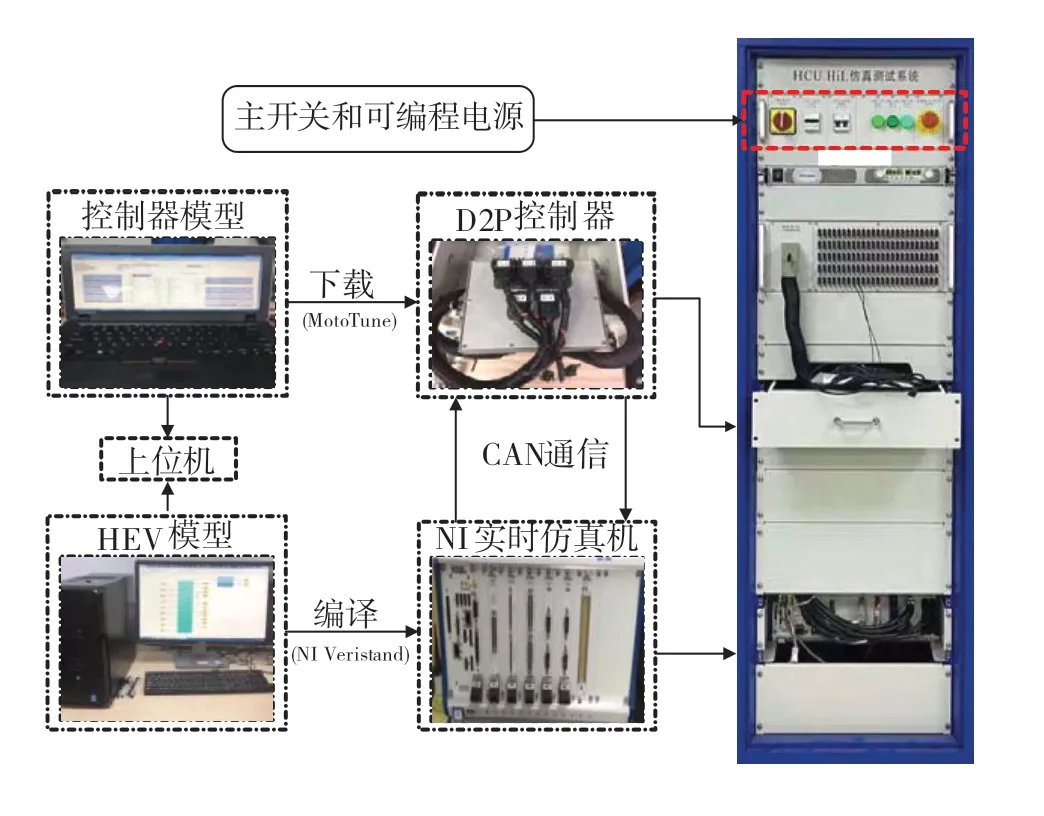
图10 HIL测试原理图

图11为本文设计的动态协调策略的仿真与HIL测试结果对比。图11（a）～图11（e）分别为发动机、电机MG1和MG2的转速、转矩和冲击度信号，由于HIL测试的硬件配置问题以及信号经过传输时存在误差，而且Motohawk平台中积分与微分模块计算能力相对仿真软件存在误差，HIL测试的整个切换过程相对实际仿真更快，关键零部件转速以及转矩也存在不同程度上的频繁波动，但其变化趋势基本一致，测试结果依旧在可接受范围内。从冲击度角度来看，不同加速工况下的最大模式切换冲击度为9.34 m/s3，仍小于德国标准（10 m/s3）。因此，HIL测试结果表明本文提出的动态协调策略不仅能够满足模式切换控制需求，提高模式切换品质，还具有较好的工况适应性。

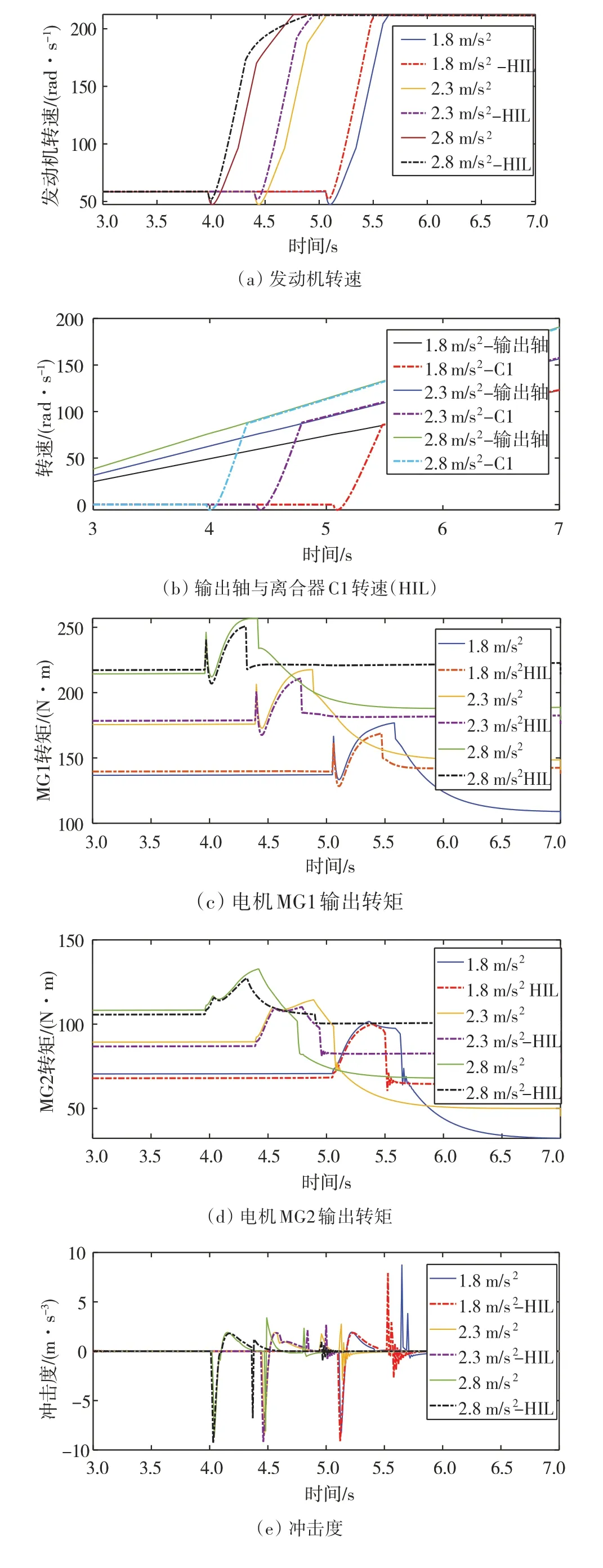
图11 仿真与HIL测试结果

5 结论

（1）针对一款集成多离合器的功率分流式HEV，根据杠杆法和矩阵法建立了涉及双离合器协同的纯电动模式切换至混合动力模式的切换阶段动力学模型，确定了模式切换序列和切换逻辑，制定了不同切换阶段各动力源和离合器动态协调控制策略。

（2）针对双离合器协调滑摩的切换阶段，基于模拟退火算法优化了考虑模式切换冲击度、滑摩功和切换时间的离合器滑摩行为，并设计了混合动力模式下适应不同需求转矩的发动机转速自适应调节策略，通过自适应动态调节电机MG1转矩提高大范围工况模式切换平顺性。

（3）在仿真分析的基础上，搭建了HIL测试平台，进行了所提出策略的试验验证，结果表明，发动机转速、输出轴端转速以及行星架C1转速均能够满足切换控制需求，而且不同加速工况下冲击度的绝对值都能够控制在10 m/s3下，能够提高大范围加速工况的整车行驶平顺性。