基于Copula的横断山区非平稳性气象干旱特征
刘瑞琳, 孙 鹏, 张 强, 卞耀劲, 马梓策, 邹逸凡, 吕胤峰
(1.安徽师范大学 地理与旅游学院, 安徽 芜湖 241002;2.江淮流域地表过程与区域响应安徽省重点实验室, 安徽 芜湖 241002;3.北京师范大学 地理科学学部, 北京 100875; 4.北京师范大学 环境演变与自然灾害教育部重点实验室, 北京 100875)
干旱发生的频次高、持续时间长、影响范围广,会对区域的自然生态环境,农业和社会生产等方面产生负面影响,引起了人们的广泛关注[1-3]。IPCC第五次报告中指出的全球变暖和温室气体排放量的增加,会导致极端气候的增多,各地区干旱风险都有可能增加[4-5],因此干旱事件得到了国内外学者的广泛关注。目前有很多的干旱监测指数,例如SPEI(标准化降水蒸发蒸腾指数)[6];SPI(标准化降水指数)[7];PDSI(Palmer干旱严重程度指数)[8-9];CI(综合气象干旱指数)等[10],但是对于某一指标来说,例如PDSI为固定的时间尺度,因此对发展或者减少中的干旱反映比较迟钝;SPI则是根据长期降水数据计算各种的时间尺度的降水序列,但是会忽略蒸发的影响,对于模拟干燥条件下的降水分布可能会产生较大差异;SPEI考虑了多时间尺度的地面蒸散对于干旱的影响,但是却对地面的增温过于敏感[11],随着全球气候变化,越来越多学者意识到干旱的趋势变化是一个非平稳的过程,例如鲁帆等基于极端降水等提出了非平稳的时间序列极值统计模型[12],Bazrafshan J等提出NRDI应用于南澳大利亚的气候[13],Liu Y等提出了基于物理的自校正的帕尔默干旱严重指数及其性能评价等[14]。对于干旱事件的干旱特征的概率分布可以利用单变量边缘分布函数进行估算,同一干旱事件的不同特征有一定的相关性[15],但是单变量边缘分布函数具有一定的局限性,通常采用Copula函数分析多变量的联合分布频率[16],例如王晓峰等利用Copula函数联合干旱历时和干旱烈度计算重现期对陕北地区干旱风险进行评估[17],姚蕊等利用Joe-Copula分析了淮河流域的水文干旱频率特征等[18]。
我国是干旱事件较为频发的国家,近几十年以来,极端干旱事件发生的频率增多[19-20],并有从西北向西南蔓延的趋势,横断山区位于我国青藏高原的东南缘,是我国西南纵向岭谷的重要组成部分,自然资源丰富,其自然环境、农业和社会生产生活等都受到极端干旱事件的制约[21-23],目前,对于横断山区干旱特征的研究主要包括在气温,降水[24],潜在蒸散发等[25]常规的单一要素方面,横断山区纵向岭谷的“通道—阻隔”效应对气候环境的影响[26],以及横断山区干旱河谷的干湿状况和影响因子等[27]。SPEI结合PDSI和SPI的优点,且具有多时间尺度,是目前较为成熟的干旱监测指数[28],NSPEI是在SPEI基础上的改进,适用于平稳性和非平稳性,克服了SPEI对温度过于敏感,以及对干旱程度和干旱历时的高估,同时经过平稳性检验后发现非平稳性主要在我国青藏高原和横断山区等地区,而目前的非平稳性指数,大多是基于GAMLSS模型或者气候因子建模,在算法上较为复杂,在气候因子的数据方面也有一定的局限性[11],因此本文基于NSPEI(非平稳性标准化降水蒸散发指数)分析横断山区干旱的时空分布特征,利用单变量边缘分布函数和Copula分布函数计算横断山区干旱历时和干旱烈度重现期,表征横断山区干旱的空间分布特征,为该地区的区域规划和干旱防控治理提供参考,以减少区域的自然和经济损失[29]。
1 资料来源与研究方法
1.1 数据来源
本文所涉及到的气象数据是由国家气候中心(NCC)和科考市州气象局提供的横断山区的94个气象站点(图1)的降水、蒸发、湿度、太阳辐射、日照时数、最低气温、最高气温、平均气温和风速等逐日数据。

图1 横断山区气象站点分布
1.2 研究方法
1.2.1 非平稳性的标准化降水蒸散指数(NSPEI) 本文采用的是在SPEI[11]基础上修正的非平稳的SPEI指数计算1961—2019年年逐日潜在蒸散量,与SPEI一样NSPEI具有多时相特征,可以考虑不同的干旱类型,NSPEI既考虑了降水也考虑了温度对于干旱影响,同时考虑了干旱过程的非平稳性,能够有效的增加对干旱事件的识别、提高预测的精度。
计算过程为:Dt指的是不同时间下的降水与蒸散发的差[11]。
Dt=Pt-PETt
(1)
式中:Dt是时间序列;P降水;PET是潜在蒸发量。
根据式(2)对Dt拟合,
(2)
式中:S为太阳辐射;t为时间;h为平滑参数;tmax为最高气温;tmin为最低气温;f为Dt的线性拟合函数。
时变的位置参数:
γDt=loess(Dt)
(3)
基于时变的Dt分布函数
(4)
式中:α,β,γ分别是尺度,形状,位置参数。本文采用经验频率的概率加权矩法(PWMS)估计参数α,β,γ,PWMS具体计算公式如下:
(5)
式中:ws是s阶的PWN,其中s=4;N是数据的长度。
Dt均值随时间序列变换,平滑样条函数拟合的趋势值即位置参数是不断变化的,只有当均值不变时,位置参数才保持不变,那么NSPEI和SPEI值保持一致,利用K-S判断是否符合Log-logistic分布。
(6)
(7)
式中:F为频率估计,当p≤0.5,P为累积概率,p=1-F(x);当p> 0.5,则p=1-P;其他参数为C0= 2.515 517,C1=0.802 853,C2=0.01028,d1=1.432788,d2=0.189269,d3=0.001308,计算NSPEI。NSPEI的干旱分类(表1)。

表1 NSPEI干旱等级划分
1.2.2 干旱的定量表征 干旱的定量分析主要是通过干旱事件的属性来进行表征的,本文主要指的是干旱强度、干旱频率[29],干旱强度Q主要表示的每月的干旱的严重程度,根据NSPEI干旱等级划分(表1),是指NSPEI<0时NSPEI的累计值(式8),
(8)
式中:NSPEIij为小于0的NSPEI值;i=1,2,3,…,12表示12个月;j=1961,1962,…,2019表示时间序列长度;
干旱频率P表示的不同程度的干旱事件在总的干旱事件的比例(式9),
(9)
式中:m为干旱事件的月数;M为总月数。
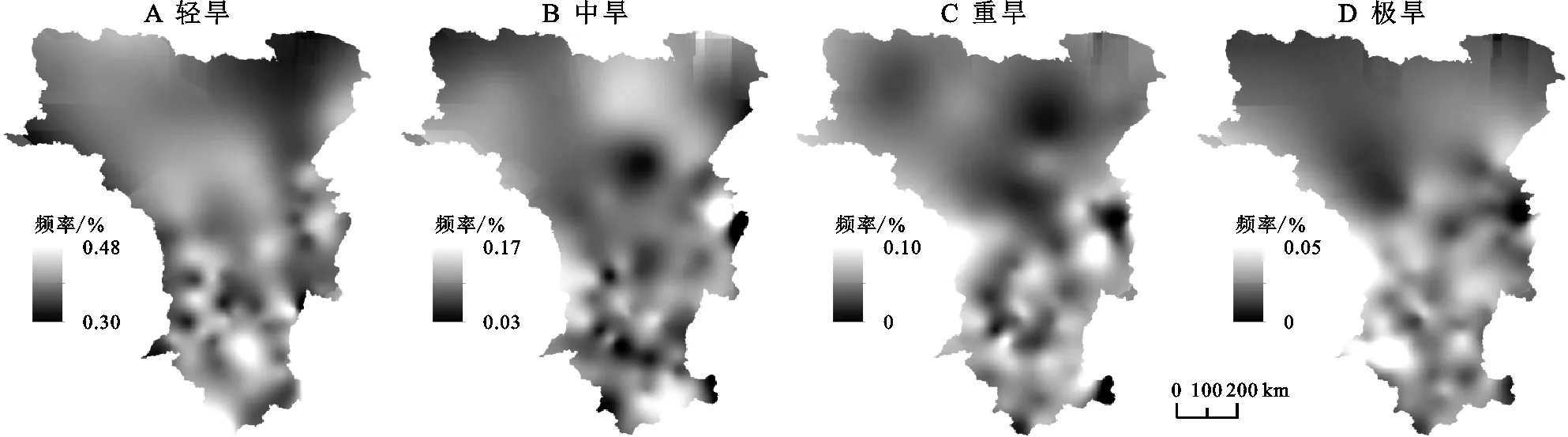
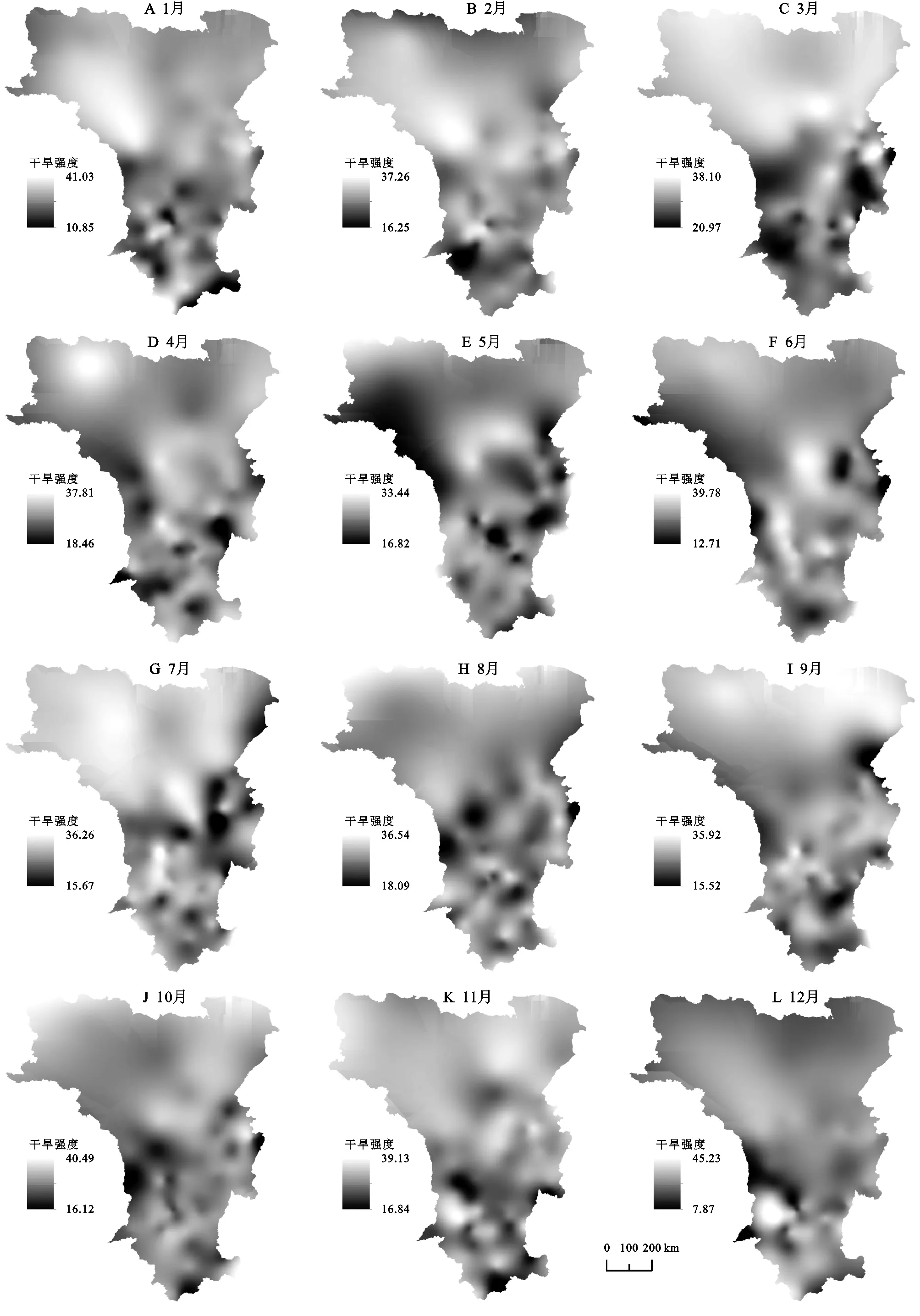
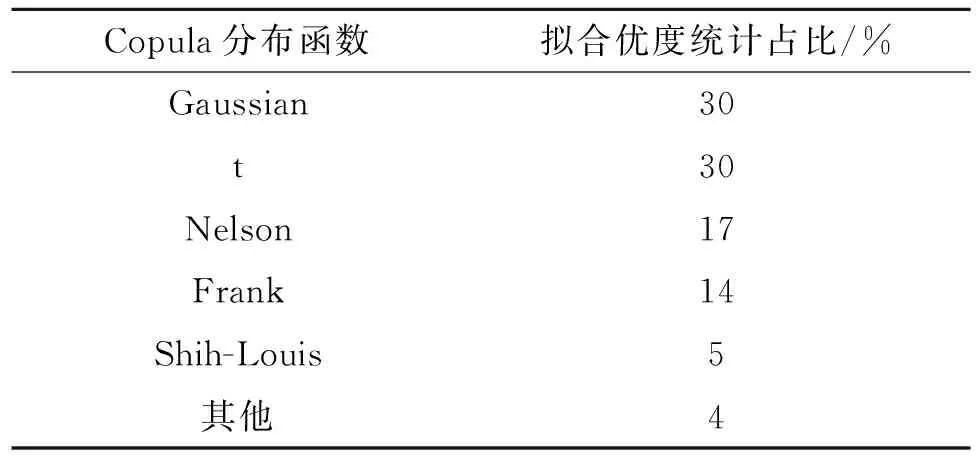
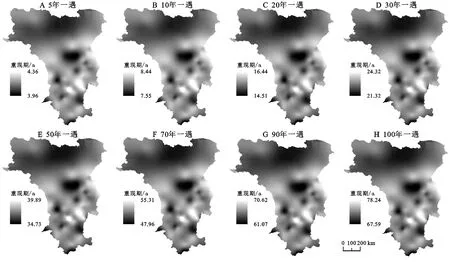
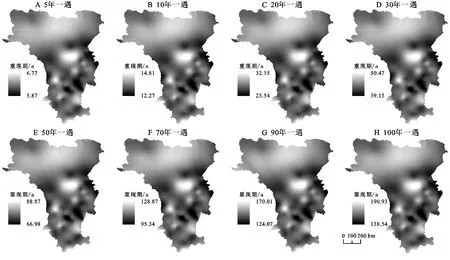
1.2.3 干旱特征的识别 游程理论是一种有效的时间序列分析方法[16],Yevjevich最早提出这一理论,可以用于识别干旱事件的干旱特征。由图2可知,根据NSPEI的干旱等级的划分(表1),确定R0为截取水平,用于识别干旱事件,当R 图2 游程理论干旱示意图 干旱历时D表示的一次干旱时间开始到结束的时间,即t2-t1;干旱烈度S表示的是一次连续的干旱时间的NSPEI的累计值(式10), (10) 式中:D为干旱历时;S为干旱烈度。 1.2.4 分布函数 单变量频率分布函数。建立联合分布之前需要先确定不同干旱特征的各自的边缘分布函数,根据游程理论确定的横断山区干旱事件的干旱特征,选取Birnbaum-Saunders,Exponential,Extreme value,Gamma,Generalized extreme value,Generalized Pareto,Inverse Gaussian,Logistic,Log-logistic,Lognormal,Nakagami,Normal,Rayleigh,Rician,t location-scale,Weibull这16种应用较为广泛的概率分布函数进行拟合,利用NLogL,BIC,AIC,AICc检验概率分布函数的拟合优度,当NLogL,BIC,AIC,AICc的值越小,拟合优度越高,利用线性矩来估计分布函数的参数,因为线性矩是最为稳健的参数估计方法[18]。 1.2.5 Copula函数 对于24种Copula分布函数Gaussian,t,Clayton,Frank,Gumbel,Independence、AMH,Joe,FGM,Plackett,Cuadras-Auge,Raftery,Shih-Louis,Linear-Spearman,Cubic、Burr,Nelsen,Galambos,Marshal-Olkin,Fischer-Hinzmann,Roch-Alegre,Fischer-Kock、BB1,BB5,利用max-Likelihood,AIC,BIC,RMSE,NSE检验分布函数的拟合优度[18]。 Copula是在[0, 1]区间上均匀分布的边缘分布函数,按照 Sklar定理,设H为一个n维的分布函数,F1,F2,…,Fn为其变量的边缘分布[23],那么一定存在一个n维的Copula分布函数C,使得对于任意x∈Rn都有: F(x1,x2,…,xn)=C[(F1(x1),F2(x2),…,Fn(xn)] (11) 如果变量的边缘分布F1,F2,…,Fn是连续的,那么C是唯一的,相反的,如果C是一个n维的,那么变量的边缘分布F1,F2,…,Fn就是其分布函数。 1.2.6 重现期计算 在气象干旱事件中,两变量的Copula联合分布,对于干旱特征中干旱历时(D)或干旱烈度(S)不超过某一特定值,即联合重现期T0;干旱特征中干旱历时(D)和干旱烈度(S)都不超过某一特定值[23],即同现重现期Ta计算公式分别为: (12) (13) 单变量干旱历时重现期和干旱烈度重现期: (14) (15) 图3表示的是横断山区1961—2019年不同等级干旱频率的空间分布状况,由图可知不同等级的干旱在研究区上存在差异性。从总体上来看,轻旱在横断山区内发生的频率最高,包括了横断山区的北部,中部和南部的大部分地区,轻旱、中旱发生的总频率最高可达65%,在空间分布上,横断山区北部呈现块状分布特征,中部和南部呈现南北向的带状和点状分布特征。 图3 1961-2019年各等级干旱发生频率分布 从不同等级的干旱事件上来看,轻旱发生于整个横断山区,即在1961—2019年横断山区都发生过干旱,轻旱发生的频率约30%~48%,轻旱频率的高值区主要分布在横断山区的北部的大部分地区,中部主要呈现的是两个南北走向的带状的分布,南部呈现块状和带状分布,高值中心的轻旱频率大约为48%;中旱在横断山区的东北部和中西部地区以及西南部地区发生的频率要明显高于其他地区,大约是在17%左右,即中旱频率与轻旱频率的空间分布具有相似性;重旱和极旱频率的空间分布和轻旱、中旱频率存在很大的差异性,尽管横断山区北部轻旱和中旱频率较大,但重旱和极旱频率很低,甚至在部分区域没有发生过重旱和极旱事件,重旱主要在横断山区的北部的西缘地区,即在青藏高原的边缘,除此以外,横断山区中部和南部的大部分地区发生重度干旱的概率大约在5%~10%,大致为南北向的带状分布;显然横断山区发生过极旱的地区相比于其他程度的干旱事件缩小很多,并且各地发生极旱的频率都很低,约为1%~4%。 图4表示是1961—2019年横断山区不同月尺度干旱的空间分布,从总体上来看,不同月尺度的干旱在空间分布上具有一定的差异性,横断山区北部在不同的月尺度下干旱的分布范围大于横断山区的中部和南部。 图4 1961-2019年干旱强度的月尺度空间分布 不同月尺度从空间上来看,1月份干旱的高值区位于横断山区的北部北纬28o以北的青藏高原区、中部山岭之间的河谷地区,以及横断山区的西南部;2月份横断山区北部干旱高值区的范围进一步向南扩大;3月份横断山区中部和南部干旱高值区的范围缩小;到4月份北部的干旱高值区范围减少,横断山区中部和南部干旱范围扩大,尽管干旱高值区仍占据了北部的大部分地区;5—6月份干旱高值区范围进一步缩小,在研究区的北部最为明显,干旱程度较于1—4月明显减弱;7月份,尽管北部的干旱高值区范围所有增加;8月份干旱范围在中部和南部进一步增加;9月份干旱高值区又开始缩小,主要集中在横断山区的北部和中部的部分地区;10—11月份干旱高值区在横断山区的西北部、东北部呈现块状分布,中部偏东、南部偏西则呈现条带状分布;12月份北部的干旱范围减少,中部和南部空间特征具有一定的一致性。不同月尺度的干旱程度的空间分布主要受到地形起伏的影响,导致气流移动过程受到的阻碍,形成特殊的屏障和通道[23],导致温度和降水分布的不均匀。 从数值上来看,10—1月、6—8月的干旱程度高于其他月份,干旱高值中的最高值和最低值相差12,说明冬夏季干旱的程度要高于其他季节,主要是因为冬季温度低,蒸发少,同时横断山区主要是受到季风气候、山地气候和高原气候的影响,冬季的降水量少,气温低,导致干旱程度的增加,夏季主要是因为温度高,虽然西南季风和东南季风带来的降水量大,但是由于横断山区青藏高原以及纵向山岭的阻挡,导致迎风坡降水多,背风坡降水少形成雨影区,容易在背风坡和河谷地区发生干旱。 总而言之,不同等级的干旱事件发生的频率在空间的分布上存在明显差异,轻旱、中旱的空间差异性不显著,表明在横断山区,虽然轻旱、中旱在不同的地区发生的频率都发生变化,但是总体来说发生的频率的空间分布差别不大,即各地都几乎不同程度发生过轻旱和中旱,随着干旱等级的增加,其空间分布的差异性逐渐明显,主要是随着干旱程度的增加,其空间分布的范围在逐渐缩小,即重旱、极旱并不是在所有的地区都发生过,各地区发生的频率明显不同。由此可见,横断山区地形的起伏和纵向山谷的分布特征所导致的降水量的不均匀和气温分布的差异,影响了不同干旱等级的空间差异性,致使干旱频率的空间分布具有一定的地域性。 不同区域和不同研究对象对于概率分布函数的选择是不同的,因此在决定频率分布函数之前进行分布函数拟合优度的分析是很有必要的。表2表示16种分布函数拟合优度的统计结果,干旱烈度中GEV为拟合最优的站点占总站点的91%其他的分布函数为最优分布函数的为9%,因此本文选择GEV来研究干旱烈度;干旱历时中GP为最优分布函数的站点占55%,其他分布函数为最优分布函数为45%,因此本文选择GP来研究干旱历时。 表2 94个站点干旱历时和干旱烈度16种分布函数拟合优度统结果 图5和图6分别表示的是干旱历时对应的单变量重现期和干旱烈度对应的单变量重现期。由图5可知,从空间上来看,干旱历时的重现期小于10年一遇,随着重现期的增加,干旱历时和干旱烈度的高值区范围也有所增加,从北部以中和南部的部分地区向横断山区的其他地区扩大,当重现其大于20年一遇,干旱历时的高值区随着重现期的增加,其空间分布保持一致,即在横断山区中部和南部呈现点状的分布特征,主要是受到特殊的地形和水文分布状况的影响,表明随着干旱重现期的增加,横断山区北部的青藏高原地区以及横断山去中部和南部的河谷和背风坡遇到长历时干旱事件要明显高于横断山区的中部和南部的山地迎风坡和河流流经地。 图5 横断山区94个站点干旱历时对应的单变量重现期 由图6可知,由于在空间分布上干旱历时和干旱烈度的空间分布具有一致性,即当重现期小于10年一遇时,干旱烈度的范围由北部向中部和南部逐渐扩大,小于百年一遇的重现期的干旱烈度在空间分布上几乎保持一致,即在同一重现期下,中西部和南部的部分地区发生强烈度干旱事件的概率要明显小于其他地区。同时,从数值上来看,横断山区的中西部干旱烈度的增加最为显著,大约增加了280,说明在百年一遇的情况下,横断山区的中西部相比于其他地区更难遇到强烈度的干旱事件。 图6 横断山区94个站点干旱烈度对应的单变量重现期 2.3.1 二维Copula函数的确定 不同的干旱特征具有一定相关性,尽管在气象干旱中采用Archimedean Copula函数是比较普遍的,但是不同的情况下也要考虑不同的Copula函数,因此为了重现期拟合的准确性,本文对24种Copula分布函数,利用贝叶斯理论和马尔科夫蒙特卡洛(MCMC)方法,根据AIC,BIC,NSE和maxi-Likelihood选择出最佳的Copula函数[18]。表3统计Gaussian和t分布函数在横断山区94个站点当中的为拟合最佳的概率相同且明显高于其他的Copula函数,本文采用的是Gaussian分布函数。 表3 横断山区干旱特征24种Copula分布函数检验统计结果 2.3.2 横断山区干旱特征的重现期分析 图7与图8表示了横断山区1961—2019年二维联合分布重现期和同现分布重现期,利用Copula函数中的Gaussian函数进行重现期的拟合。 从总体上来看,联合重现期<预定重现期,即研究区内发生长历时或者高烈度的概率较高;同现重现期>预定重现期,即研究区内发生长历时且高烈度概率很小,显然同现重现期要远高于联合重现期,即横断山区发生长历时低烈度或者短历时高烈度的概率要显著高于发生长历时高烈度的概率,在空间分布上,联合重现期和同现重现期的空间分布特征正好相反。从空间分布上来看,由图7可知,在不同的重现期下,研究区域的空间分布保持一致性,联合重现期高值区位于横断山区的中西部缘区和中南部的部分地区呈现点状分布的特征,联合重现期的低值区则位于横断山去的北部,即横断山区的北部发生长历时或者高烈度的干旱事件概率要高于横断山区的中部和南部大部分地区。由图8可知,同现重现期的空间分布也在不同重现期下保持空间上的一致性,但不同的是,其空间分布特征与联合重现期相反,即在横断山区原本部分的低值区成为高值区,高值区成为低值区,即联合重现期下,横断山区的北部要高于横断山区中部和南部的大部分地区。 图7 1961-2019年横断山区二维联合分布重现期 从时间上来看,由图7可以知,当预定重现期大于50年一遇时,联合重现期发生的概率减少的速度在明显减缓,在联合重现期小于50年一遇的时,在横断山区的南部干旱历时或者干旱烈度达到50年一遇的概率几乎都小于0.029,同时随着二维的联合分布重现期的增加,其发生的概率越来越低,当其联合重现期达到百年一遇时,其联合重现期发生的概率几乎小于0.015。图8可知,当预定重现期大于10年一遇时,同现重现期发生的概率减少的速度在明显减缓,在联合重现期小于10年一遇的时,在横断山区的北部干旱历时并且干旱烈度达到10年一遇的概率几乎都小于0.083,同时随着干旱历时和干旱烈度的联合重现期的增加,其发生的概率越来越低,当干旱历时和干旱烈度的联合重现期达到百年一遇时,其联合重现期发生的概率几乎小于0.007,整个横断山区百年一遇的同现重现期发生的概率最低甚至达到0.005,几乎不可能同时发生百年一遇的干旱历时且百年一遇的干旱烈度的事件。 图8 1961-2019年横断山区二维同现分布重现期 (1)横断山区1961—2019年干旱频率发生达到了60%以上,其中轻旱和中旱的频次占到了50%以上,总体上来看,横断山区的南部发生干旱的频次明显高于北部,即南部>北部,不同程度的干旱在横断山区发生的频率的空间分布具有一定的而差异性,重旱和极旱主要集中在南部,北部几乎不发生,轻旱和中旱几乎整个横断山区都发生过,但是依然南部高于北部。横断山区1961—2019年不同尺度的干旱程度空间上也有存在差异性,春季(3—5月),干旱重心由北向中部向南部转移,干旱程度也在逐步缓解,夏季(6—8月)干旱重心由南部向北部逐渐增加,干旱程度的变化不大,秋季(9—11月)干旱重心的空间分布变化不大,东北部、西北部、中部和南部的部分地区高于其他地区,冬季(12—2月)干旱重心由南部向北部转移,干旱程度在逐渐减缓,夏季和冬季的干旱程度普遍高于春秋季。 (2)对横断山区94个站进行分析,根据NLogL,BIC,AIC,AICc判断在16个单变量分布函数中GP对干旱历时的拟合最佳,GEV对干旱烈度的拟合最佳,根据max-Likelihood,AIC,BIC,RMSE,NSE判断在25个Copula函数中Gaussian函数为拟合效果最优的分布函数。 (3)干旱历时的高值区在重现期小于10年一遇时,随着重现期的增加,其范围也在逐渐扩大,大于20年一遇时,空间分布具有一致性,总体上来看南部>北部,即在同一重现期下,南部的出现长历时的概率要小于北部。空间上,干旱烈度与干旱历时几乎相同,即横断山区南部出现高烈度的概率要小于北部。联合重现期在不同的重现期下保持空间分布的一致性,横断山区的中西部缘区和中南部的部分地区联合重现高于横断山区的其他区域,同现重现期也保持了空间分布的一致性,但联合重现期与其空间分布特征正好相反。随着重现期的增加,联合分布与同现分布概率不断减小,并且同现分布概率要小于联合分布概率,说明发生长历时高烈度的干旱事件概率要明显低于长历时低烈度和短历时高烈度的干旱事件。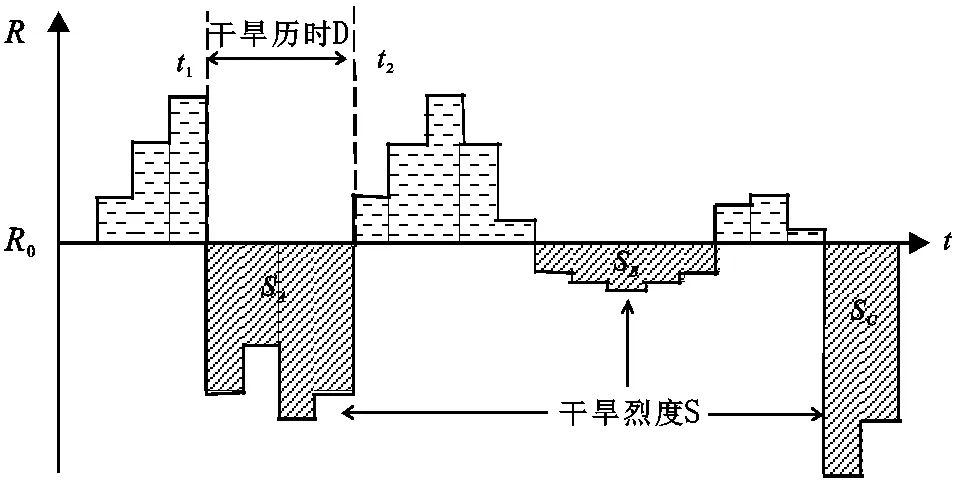
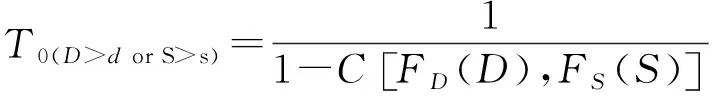
2 结果与分析
2.1 干旱特征的时空分布
2.2 干旱特征的单变量分析



2.3 二维Copula函数干旱特征频率分析
3 结 论

