基于宏弯损耗原理的光纤微力传感器

杨 毅

(湖北工业大学机械工程学院，湖北武汉 430068)

0 引言

微操作/微装配技术是先进智能制造领域内的关键技术，属于微观范畴的超精密加工操作，涉及微驱动、无损夹持、微力测量和视觉伺服等技术难点[1]。其中，微力测量为微操作/微装配提供接触作用力信息，是实现微操作/微装配的重要环节。目前，微力传感器主要有压电式[2-3]、电容式[4-5]、压阻式[6]和基于视觉[7-8]的微力传感器等，以上方式对于微操作/微装配都有一定的局限性。经过对比，发现光纤传感具有的高灵敏度、抗电磁干扰、高精度、耐高温、耐腐蚀及小巧等特点，非常适合微操作/微装配中微力的传感。

在设计上，可将光纤传感器嵌入微夹持臂实现微力感知，由此可利用光纤的宏弯损耗来实现微力传感，其原理见文献[9]，根据光纤随着弯曲半径减小而损耗增加的特性可实现微力传感，并且其结构简单，可集成到微操作/微装配系统中。

文中提出了基于宏弯损耗原理的光纤微力传感方法，根据光纤宏弯损耗特性，结合悬臂梁弯曲的力学模型，建立了光纤微力传感器测量微小力的测量模型，研制了基于阶跃单模光纤宏弯损耗的光纤微力传感器，并进行了测试。

1 传感器基本原理

1.1 传感器原理及结构

基于宏弯损耗的光纤微力传感器的原理与结构如图1所示，将单模光纤末端(如图1中B端)切平并去除涂覆层，并将光纤的A端固定即形成光纤微力传感结构。当垂直于光纤轴向的力F作用于B端时，光纤微力传感结构将产生弯曲，由于弯曲损耗，从B端反射回光电探测器的光功率PR将会下降。通过建立反射光功率PR与被测微小力F之间的关系模型，可实现微小力的传感。

图1 基于宏弯损耗的微力传感器结构示意图

1.2 传感器模型建立

为建立光纤微力传感器的微小力测量模型，首先根据传感结构和光纤宏弯损耗理论，建立光纤宏弯损耗与功率的关系模型；然后建立光纤宏弯损耗与曲率半径的关系模型；其次结合工程力学和材料力学建立光纤微力传感结构所受力与曲率半径的关系模型；在此基础上，建立基于光纤宏弯损耗的微力传感模型。通过探测功率变化，获得测量的微小力大小。

1.2.1 宏弯损耗与功率的关系

由光纤宏弯损耗理论[10]可知，弯曲损耗因子与传输光功率的关系为

(1)

式中：P为输入端光功率；ΔP为损耗的光功率。

为精确描述宏弯损耗因子，提出通过微元方法将受力的光纤传感结构划分为一定数量的微型弧段，如图2所示，设从光纤A端到B端，每一段微型弧段到A端截面的长依次为x1、x2、…、xn-1和xn，相应的各微型弧段的弯曲损耗因子依次为2α(x1)、2α(x2)、…、2α(xn-1)和2α(xn)，具体各段微型弧段的入射光功率依次为Pi0、Pi1、Pi2、…、Pin-1和Pin，而从B端到A端，各段微型弧段的反射光功率依次为Pr0、Pr1、Pr2、…、Prn-1和Prn，则根据式(1)可得：

(2)

将式(2)整理得：

(3)

由式(3)累乘推导：

(4)

设光纤微力传感结构AB弧段的宏弯损耗因子为2αAB，则有：

(5)

若使式(5)中n→∞，即将光纤微力传感结构划分为无限多个小弧段，则可以获得2αAB的精确表达式：

(6)

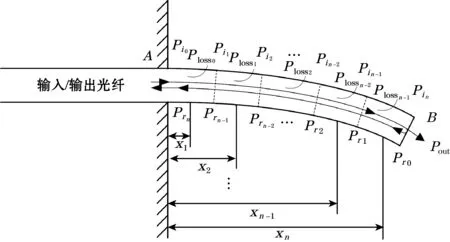
图2 光纤微力传感结构弯曲时的光传播示意图

光纤不发生弯曲时的反射光功率与发生弯曲后的反射光功率关系为：

(7)

式中：P0为光纤传感结构未弯曲时的反射光功率；PR为弯曲后的反射光功率；r为光纤截面反射率。

由于图2所示的微小力传感方法中，光纤悬臂微力传感结构发生弯曲前后的反射传输功率P0和PR是容易获得的，为了得到宏弯损耗因子2αAB，需要建立P0和PR与2αAB之间的关系，由式(5)和式(7)可得：

(8)

1.2.2 宏弯损耗与曲率半径的关系

由文献[11]可知，当光纤存在涂覆层时，光纤宏弯损耗随弯曲半径和光源波长的变化会产生振荡，考虑到微纳操作/微纳装配中力传感的稳定性，选择将光纤的涂覆层去除，以实现更好的力传感。

去除光纤涂覆层后，若将单模光纤绕成一个圆环，其宏弯损耗因子可表示为[10]

(9)

式中：a为纤芯半径；R为宏弯曲率半径；β为单模光纤传播常数；V为归一化频率。

参数k、γ和eυ定义为：

(10)

(11)

(12)

式中：υ为模式的阶数；n1、n2分别为光纤纤芯与包层折射率；k0为真空波数。

k0可表示为

(13)

式中λ为传输光波长。

在阶跃单模光纤中，β>n2k0，因本文采用SMF，只支持基模传输，所以υ=0，eυ=2，则V计算式为

(14)

综上所述，对于给定的阶跃单模光纤，当传输光波长λ确定，则2a和R存在对应关系。光纤传感结构弯曲时，距离A点长度为x的某点，其R应为x的函数，记为R(x)，则根据式(9)，该微型弧段的2α可表示为

(15)

式中ΔL为半径为R(x)微型弧段的弧长。

1.2.3 力与曲率半径的关系

根据图1，光纤在纯弯曲情况下，悬臂梁上任意一点的弯矩M(x)与施加于自由端B处的微小力F的关系可表示为

M(x)=F(l-x)

(16)

式中：l为光纤悬臂的长度，即光纤微力传感结构固定端A和自由端B之间的距离。

悬臂梁的曲率半径R与弯矩M有如下关系：

(17)

式中：I为光纤截面的惯性矩；E为弹性模量。

综上所述，悬臂梁上与固定端A的距离为x的点，其R(x)与自由端施加的微小力F存在对应关系：

(18)

1.2.4 基于宏弯损耗的微力传感模型

(19)

根据式(19)，可以通过光电探测器探测光纤弯曲前后的反射传输功率P0和PR来表征微小力F的大小。光纤微力传感器制作后，只要光纤微力传感器接触对象的位置确定，即l确定，即可由式(19)确定微小力大小。

由理论分析可知，影响阶跃单模光纤宏弯损耗因子2αAB的参数主要包括：光纤微力传感结构B端受到的力F；光纤微力传感结构固定端A和受力端B之间的距离l；激光波长λ；纤芯半径a。其中，F是被测量，l、λ和a都是可优化量。此外，E、I、n1、n2等参数的变化也会对2αAB造成影响，但这些参数是光纤本身固有特性决定的，当光纤确定时即为已知参数。

2 数值仿真与分析

光纤微力传感器的主要参数如表1所示，光纤微力传感器采用SMF-28单模光纤加工，仿真软件为MATLAB。

表1 光纤微力传感器的主要参数

根据表1参数以及微力传感原理模型(式(19))仿真得到的宏弯损耗和微小力与悬臂长度的关系曲线如图3所示。由图3可知，当力和悬臂长度其中之一为定值时，另外一个参数与宏弯损耗都为一一对应关系，为一条曲线。此外，力和悬臂长度的增加都会导致宏弯损耗的增大，符合实际的情况。

图3 宏弯损耗与力和悬臂长度关系仿真

为分析光纤结构参数对光纤宏弯损耗因子2αAB的影响，分别对a和λ与2αAB的关系进行了仿真。图4(a)给出了3、15、30 mN微小力作用下2αAB与阶跃单模光纤纤芯半径a之间的关系。从图4(a)可看出，在阶跃单模光纤纤芯半径范围内，宏弯损耗因子随着纤芯半径增加而非线性地下降，且相同纤芯半径情况下作用力越大，2αAB越大。图4(b)给出了3、15、30 mN微小力作用下宏弯损耗因子与激光波长之间的关系。根据图4(b)可以发现，2αAB随着激光波长的增加非线性缓慢增加。根据实际需求并结合图3、图4，选择合适参数可得到所需的基于光纤损耗的微力传感器。

3 实验及分析

测试时，研制的微力传感器悬臂长度l为480 μm，其表征P0的电压为4 420 mV，测试在恒温环境下进行。

根据理论模型(式(19))预测得到的微小力F与弯曲前后的传输功率比PR/P0之间的关系曲线如图5所示，同时图5也给出了试验得到的参考微小力FR与弯曲前后的传输功率比PR/P0之间的曲线关系，PR/P0通过对传感器施加不同的力时对应的表征电压得到。由图5可知，对同一种悬臂长度，试验测得参考微小力FR与理论模型得到的微小力F基本相等。由此表明了光纤微力传感器的理论模型的正确性。

在图5的实验数据基础上，将其转换为微小力F和2αAB的关系曲线，如图6所示。根据图6，当2αAB为0时，理论模型得到的微小力和测量得到的参考微小力也为0，表明光纤微力传感器未受到微小力的作用；对同一种悬臂长度的微力传感器，当2αAB增大时，微小力在增大，且微小力与2αAB之间有一一对应的关系。

(a)2αAB与纤芯半径a关系

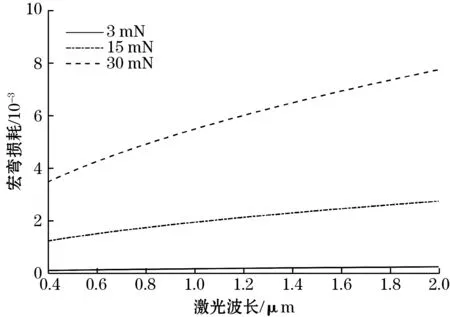
(b)2αAB与激光波长λ关系图4 不同微小力作用下宏弯损耗系数2αAB 与主要结构参数之间的关系仿真

图5 微小力F与弯曲前后的传输功率比PR/P0之间的关系曲线

总体上说，光纤微力传感器理论模型得到的微小力曲线和参考微小力曲线是非常吻合的，在光纤悬臂长度l为480 μm测试时，光纤微力传感器测量得到的微小力和参考微小力曲线的拟合度为99.98%。由式(19)可知，在理想情况下，光纤微力传感器测得的微小力F的分辨率取决于对反射传输功率的探测分辨率，而本实验中对应的基于宏弯损耗原理的光纤微力传感器分辨率为6 mN。

图6 微小力F和参考微小力与宏弯损耗之间的关系曲线

根据图5、图6及式(19)，光纤微力传感器为非线性传感器。由图5、图6可知，随着被测微小力量值的增加，微小力传感分辨率会随之提高。但是，提高传感器的分辨率会导致传感器测量范围的缩小。为了提高传感器分辨率，可以适当增加传感器的悬臂长度。由此得到表2中的传感器参数。

表2 悬臂长度480 μm微小力传感器特性参数

4 结束语

本文提出了一种基于宏弯损耗原理的光纤微力传感器，分析了悬臂梁状态下无涂覆层阶跃单模光纤的损耗，建立了光纤宏弯损耗与微小力的关系模型，测试得到悬臂长度为480 μm的光纤微力传感器的分辨率为6 mN。通过与理论对比，悬臂长度为480 μm的光纤微力传感器拟合度为99.98%。研究结果表明理论计算与测试结果一致，利用本文提出的基于宏弯损耗原理的光纤微力传感可以实现微小力的绝对测量，对微操作/微装配进行微力感知具有重要意义，并且其具有精确、灵敏、稳定等特点。