基于粒子群算法的车站列车进路搜索方法研究
方文雄,侯宇婷,蔡 煊
(成都工业学院汽车与交通学院,成都 611730)
目前,铁路信号机、岔道及轨道电路之间的制约关系广泛采用计算机联锁进行控制[1],进路搜索是计算机联锁的重要功能。文献[2]中提出了结合二叉树、四叉链表和高度原则的搜索算法,文献[3]中采用深度优先搜索方式,适用于道岔较少的车站。文献[4]中采用广度优先搜索方式,适用于股道较少的车站。文献[5]中基于站场型数据结构,提出采用高度搜索方法克服广度和深度优先算法的不足,并在规模较大站场(16股道、104组道岔)中测试了深度搜索与优化后的搜索方式的搜索耗时都在5 s左右。其实验数据说明当站场规模较大时,以上搜索算法无论是否进行优化,其搜索效率都大大降低,其原因在于,以上算法从搜索策略上均属于遍历搜索或是基于改进数据结构、优化约束条件而在局部范围进行的遍历搜索,一旦站场规模增大搜索量将呈几何增长。文献[6]依托智能优化型算法,提出基于遗传算法(Genetic Algorithm,GA)的概率型进路搜索方法,搜索结果以大概率朝全局最优结果演化,从而避免了对全局进行搜索,但没有解决智能优化型算法普遍存在易收敛局部最优的问题。粒子群算法(Particle Swarm Optimization,PSO)同属于智能优化型算法,各粒子之间通过信息共享朝向全局最优范围进行搜索,避免了对全局搜索。本文将粒子群算法应用于进路搜索,与遍历搜索型算法相比,在站场规模增大时对搜索效率的影响更小;与遗传算法相比,能够以更小的搜索种群与更少的迭代次数完成进路搜索,且采用迭代次数控制与精度控制相结合的方式解决了搜索过程中收敛局部最优的问题。
1 车站站场数据结构分析
如图1所示以典型车站平面布置为例,结合文献[7]构建站场型数据结构。考虑模型的简洁性,本文只考虑车站列车作业,调车作业进路搜索原理及数学模型参考列车作业。
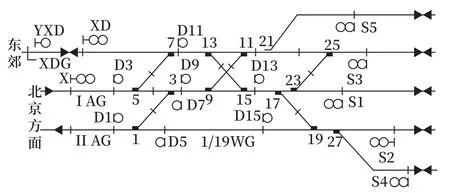
图1 车站平面布置Fig.1 Station layout
将选排进路中所途经信号机、道岔、轨道电路视为节点统一编号描述,编号原则为由下向上、由左向右的顺序对节点按序编号。在某一轨道电路上可能同时存在防护本轨道区段的信号机与道岔,即在同一轨道区段中包含3种信号设备节点,为了避免在同一位置冗余定义节点,在定义过程中优先选择道岔作为节点,再选择轨道电路,最后再考虑信号机。为了描述信号设备之间的前后位置联系,将其他节点与本节点的位置联系信息存储于本节点数据中,同时只考虑单向连接,即只在本节点存储与本节点相连的前一节点编号,不存储与本节点相连的下一节点编号。数据结构如图2所示。
图2中每一节点数据定义为(pf1,pf2,i),其中pf1为水平方向上所连接的前一节点的编号,pf2为渡线方向上所连接的前一节点的编号,若不存在则为0;i为本节点编号(i=1、2、3...)。在办理接车进路时,按搜索结果顺序输出途经节点。办理发车进路时,按照进站方向搜索,逆序输出途经节点。

图2 数据结构Fig.2 Data structure diagram
2 粒子群进路搜索算法建模
2.1 粒子群算法引入
粒子群算法是一种随机全局优化算法,通过粒子间的相互作用发现复杂搜索空间中的最优区域。算法描述为[8]在D维区域里存在m个粒子,如公式(1)~(6)所示。
第i个粒子的位置为一个矢量:

第i个粒子的速度为一个矢量:

第i个粒子搜索到的最优位置为:

整个粒子群搜索到的最优位置为:

第i个粒子在k次迭代时的速度为:

第i个粒子位置更新公式:

其中i=1, 2, 3…m;d=1, 2, 3…D;ω称为惯性参数;c1、c2称为学习因子;r1、r2为随机数;公式(5)中等号右边, 为历史速度的记忆、为个体认知部分、为社会认知部分。
2.2 改造粒子群算法建立模型
2.2.1 粒子编码
在标准的粒子群算法中,粒子的位置与速度是可以连续取值的,以单个粒子的移动在解空间进行搜索。而在进路搜索中由于节点位置是离散的,如果粒子位置离散取值,带来一定的困难,并且一个粒子的位置无法记录下一条进路中多个节点的位置。鉴于此,根据节点取值特点,使用二进制对节点选取进行表示。当一个节点取值为1,表示搜索的进路包含此节点,为0反之。现对搜索粒子做出新的定义:一个粒子代表一条可能满足要求的进路,表示为:x={x1,x2,x3...xD},其中xd(d=1...D)的取值表示第d个节点是否选中,D表示站场中节点的个数。如x20=1,表示编号为20的节点被选中。这样一来,一个粒子就是长度为D的0、1序列,就可以表示一条进路。进路搜索也就是在众多粒子中选择最优解问题。
2.2.2 进路搜索算法实现
设粒子种群为集合X,包含m个粒子xi={xi1,xi2,xi3...xiD},其中i=1, 2, 3…m。 表示一条可能满足要求的进路,通过不断改变粒子中的节点取值,搜索出满足要求的进路。基于粒子群算法的进路搜索算法流程如图3所示。
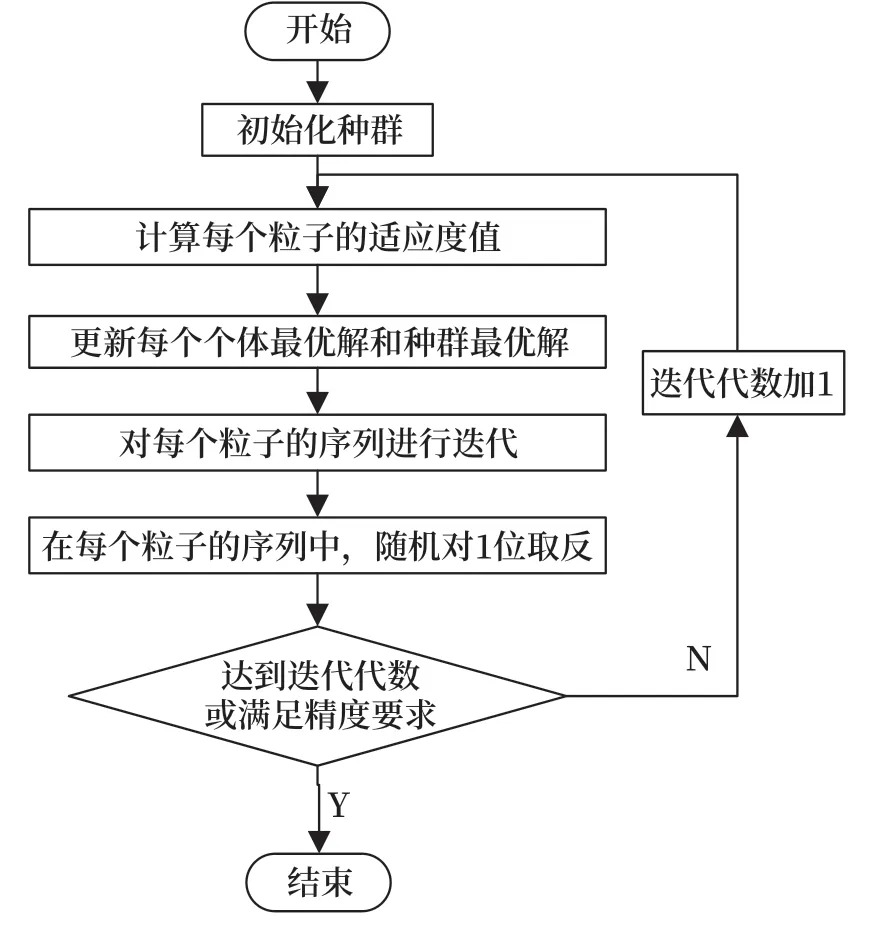
图3 算法流程Fig.3 Algorithm flow chart
由于进路搜索中粒子具有新的含义,所以要重新定义迭代公式,第i个粒子在第k次迭代如公式(7)~(9)所示。
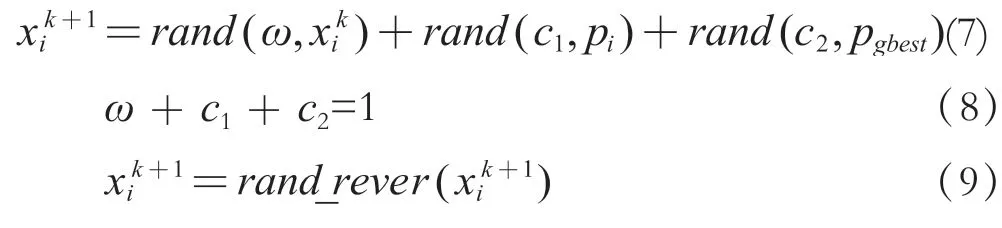
其中i=1, 2, 3…m,xi为第i个粒子的序列;Pi为第i个粒子的历史最优解序列;Pgbest为截止到第k代所有粒子中最优序列又称全局最优序列。ω为惯性参数;c1为历史最优参数;c2为全局最优参数,rand(a%,b)表示随机在b的0、1序列中,抽取占b中a%的序列。rand_rever(b)表示随机对b序列中某一位取反操作。
在公式(7)中通过rand(a%,b)的随机抽取操作,模拟标准粒子群算法中r1、r2随机数。3个参数与标准粒子群算法中类似,代表历史记忆、个体认知部分、社会认知部分所占权重,下一代粒子的序列来自于上一代粒子序列与该粒子历史最优序列和全局最优序列,并且这3部分所占比例分别为ω、c1、c2。因此这3个系数要受到公式(8)的约束。粒子群算法可能在搜索过程中陷入局部最优解,为提高粒子的搜索能力,在每次迭代过程中通过公式(9)随机对序列中某1位取反,产生突变,从而跳出局部最优解,改善进路搜索能力。
2.3 目标函数
一条合理的进路,应该是被选中的节点从始端到终端在站场位置上是相连的,即由一个粒子中值为1的节点所组成的子集,该子集的节点从始端到终端依次连接。在站场中还存在变更进路满足上述约束,为了能够选出基本进路,按照基本进路对车站作业影响最小的含义,约定所途经节点数目最小的为基本进路。所以做出约束为:在多个粒子同时满足其全为1子集的节点是相连的条件下,子集元素数目小的为基本进路。按照以上约束条件,结合适应度函数做出改进,提出目标函数如公式(10)所示。
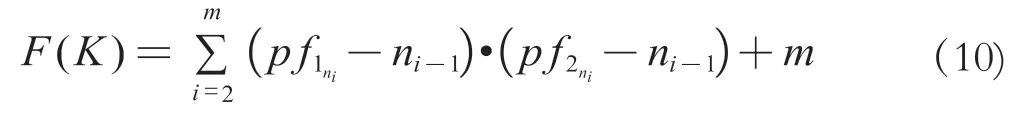
K为该粒子中取值为1的节点所构成的子集,n是K中节点对应的粒子编号集合,例如某粒子x={0, 1, 0…, 1, 0},对应的K={1, 1, 1, 1, 1}、n={2, 5,8, 9, 12}。m为K中元素的个数;ni表示n中第i个编号;pf1ni表示节点编号为ni的pf1值;pf2ni表示节点编号为ni的pf2值。
公式(10)中第一项只要本节点与前一节点相连差值就为0,当第一项中累加为0,表示能够构成所选节点相连的进路。第二项为K集合中元素的数目,用来区分基本进路与变更进路,所以当F(K)取值最小,对应的粒子为全局最优解,即搜索出能够满足约束要求的进路。
由于智能优化算法可能陷入局部最优解的普遍共性,为了确保进路搜索的准确性,必须要有精度控制的环节,即保证F(K)-m=0。单纯采用精度控制搜索结束丧失了一定的高效性,因为一旦陷入局部最优解时,需要一定时间等待跳出局部最优,再寻找到全局最优后结束搜索。为了兼顾安全性与高效性,采用迭代次数控制与精度控制相结合的方法结束搜索。先进行迭代控制,迭代N次后结束搜索,再检查搜索精度是否满足要求,如不满足要求重新执行搜索程序,重复上述过程。这样一来,一旦陷入局部最优,满足迭代次数时结束程序,重新搜索,避免长时间等待。
3 仿真与分析
3.1 实验仿真
以图1站场为例,选排北京方向下行至4G接车进路进行仿真分析。
1)初始化粒子种群数目为20个,并随机赋值粒子0、1序列,设置迭代数目30代。
2)输入搜索进路的始端、终端按钮编号2和21。
3)得出途经节点编号为{2, 4, 5, 8, 11, 12, 13,17, 21},搜索时间t=0.565 509 s,绘制目标函数收敛曲线如图4所示。

图4 目标函数收敛过程Fig.4 Objective function convergence process
4)实验结果表明:搜索算法能够正确、安全、高效地完成进路搜索,在第6代时找到全局最优解F(K)=9,且满足F(K)-m=0的精度要求。
3.2 参数最优取值范围分析
目前对于粒子群算法中,ω、c1、c23个参数合适的取值还没有科学的依据,大多凭借经验设置或动态改变取值[9]。为了确定使搜索效率最高的取值,采用控制变量法,将一个参数取定值等于0.1、0.3、0.5、0.7的情况下,改变另外两个参数取值,重复执行5次取平均搜索时间,进行参数最优范围测定。
3.2.1 控制惯性参数ω不变
测试参数c1、c2满足方程c1+c2=1-ω相对变化时的程序执行效率。结果表明:当ω在0.3~0.5时,整体搜索效果较好。测试结果如图5所示。
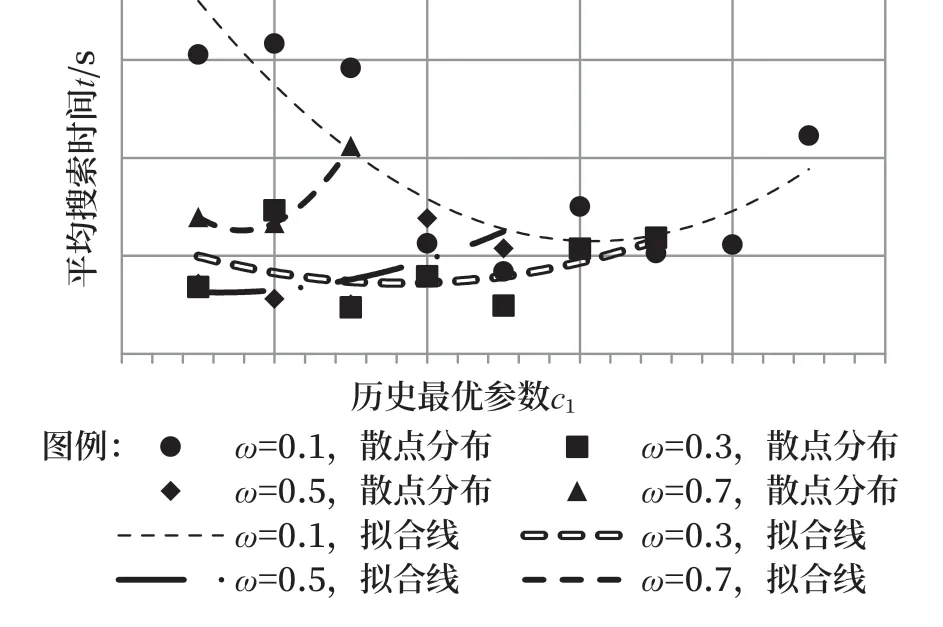
图5 ω不变,t随c1、c2取值变化Fig.5 ω does not change, and t changes with the values of c1 and c2
3.2.2 控制历史最优参数c1不变
测试参数c2、ω满足方程ω+c2=1-c1相对变化时的程序执行效率。结果表明当c2与ω差值较大时,搜索效率下降。c2在0.3~0.5时,搜索效果较好。测试结果如图6所示。

图6 c1不变,t随c2、ω取值变化Fig.6 c1 does not change, and t changes with the values of c2 and ω
3.2.3 控制全局最优参数c2不变
测试参数c1、ω满足方程ω+c1=1-c2相对变化时的程序执行效率。结果表明:当c2=0.5时,随c1增大搜索时间显著增大,c1在0.3~0.6时,整体搜索效果较好。测试结果如图7所示。

图7 c2不变,t随c1、ω取值变化Fig.7 c2 does not change, and t changes with the values of c1 and ω
3.3 参数最优统计
将被控制的参数在每一定值情况下的最短搜索时间进行统计,如表1所示。在任意被控制的参数取0.3,另外两参数之比为0.75时,具有较好的搜索效率。以表1中最少的搜索时间,给出参数最优取值为ω=0.3、c1=0.3、c2=0.4。

表 1 平均最低搜索时间t随两个参数比值变化情况Tab. 1 Average minimum search time t changes with the ratio of the two parameters
4 结束语
通过引入粒子群算法,并对粒子的含义与核心公式重新进行定义,实现了一种基于粒子群算法的新的进路搜索方法,为计算机联锁的进路搜索方法提供了新的思路。
通过精度控制与迭代次数控制相结合的方式,确保了进路搜索的准确性、安全性和高效性。进行实验统计分析,得到参数最优取值为ω=0.3、c1=0.3、c2=0.4,为基于粒子群算法的进路搜索方法工程应用提供了数据指导。
需进一步研究在其他进路锁闭情况下,进路的搜索方式,改进搜索模型,考虑在进路搜索完成后驱动信号灯、道岔状态变化。

