基于开机过程的水电机组机械振动状态评估方法

王卫玉，姚小彦，肖启志，何葵东，覃杰

（1.五凌电力有限公司，湖南长沙 410004；2.国家电力投资集团水电产业创新中心，湖南长沙 410004）

0 引言

水电机组在运行过程中由于摩擦、部件松动及疲劳等原因导致其机械振动状态发生退化，影响机组的安全稳定运行［1-5］。传统的水电机组机械振动状态分析采用离线变转速试验的方式，通过观察振动幅值及其随转速变化趋势判断机械振动状态。然而离线试验不仅需要特定的试验条件，不易频繁进行，并且耗费大量的人力和物力，而且不能实时跟踪机组长期运行下机械振动状态变化趋势。随着水电机组状态检修的需求和发展，电站往往希望实时掌握机组稳定性状态及长期运行下稳定性状态变化趋势［6-8］。因此建立水电机组机械振动状态评估模型，实现对其振动状态变化趋势实时跟踪评估及预警，对及早发现机组潜在机械故障、消除事故隐患、保障机组安全稳定运行、推进水电机组状态检修等具有重要的意义［9-11］。

水电机组开机动态过程是包含升转速、起励建压及同期的一系列过渡过程，与空载及负荷稳定运行等稳态工况相比，开机过程机组稳定性表现往往较差，但此过程监测数据却包含了丰富的机组稳定性信息，例如开机升转速阶段蕴含着机械振动在不同转速下的表现特征，对此特征进行分析挖掘可获取机械振动状态的丰富信息，不过也面临着变转速动态信号采集及幅频特征有效提取等问题。在开机过程稳定性特征提取方面，杨华［12］等在2017 年利用VMD 及HHT 结合分析了水电机组开机升转速过程振动信号，验证了VMD对升转速下振动信号频率特征提取的有效性。张海峰［13］在2007年基于HHT 研究了水电机组开停机过渡过程及稳定运行时振动信号，并利用神经网络延拓法对EMD 中存在的端点效应现象进行了改进。沈婷婷［14］在2016年针对硬件受安装场合限制的问题，提出了一种基于EMD分解和Hilbert分析的机组瞬时频率分析方法，并应用转子试验台数据进行了验证。丁光等［15］使用短时傅里叶变换分析了抽蓄机组开机过程振动、摆度、压力脉动信号的时频特征。在开机过程稳定性状态评价方面，彭兵［16］等在2007年提出了一种基于开机过程信息融合的诊断方法，基于SVM 进行了分类识别，并利用D-S 证据理论进行了结果融合诊断。肖剑［17］利用定性趋势分析及改进动态规整算法构建了一种针对开机过程性能的水电机组状态评估方法。张孝远［18］通过提取机组开机、停机过程中的振动、摆度信号的一倍频变化趋势，绘制Bode 图和Nyquist图，进行开机、停机过程该图像的对比分析，认为如果发生异常或故障，开机、停机过程Bode 图、Nyquist 图在同一转速处应存在明显差异。综合上述研究现状来看，多数是基于传统模式识别实现机组故障诊断的思路，针对水电机组开机过程的稳定性特征提取方法还需进一步结合水电机组实际情况进行改进，并且需要建立对开机过程数据深入挖掘以评价机械振动整体状态的方法。

针对水电机组机械振动状态实时跟踪评估问题，基于动态信号分析、数据挖掘及多元统计分析方法，开展基于开机升转速动态过程数据挖掘的水电机组机械振动状态评估研究。首先，提出了基于开机升转速过程的机械振动特征提取及样本构建方法，实现对水电机组机械振动幅值及阶次频率特征提取，建立机械振动状态样本；其次，引入数据挖掘中相似度度量方法，搭建了基于开机过程的水电机组机械振动状态评估模型，该模型一方面将反映振动总体剧烈程度的峰峰值作为稳定性特征变量，基于数据挖掘中距离度量方法，提出一种基于开机过程单元峰峰值变化趋势数据挖掘的机械振动状态评估方法；另一方面，为弥补峰峰值不能对振动能量在频域分布细节变化进行反映的缺陷，将动态信号分析、多元统计分析及相似度度量方法结合，进一步提出了基于多元特征阶次频率能量占比变化趋势数据挖掘的机械振动状态评估方法。最后，基于水电机组开机过程实测数据对模型的有效性及实用性进行了分析验证。

1 特征提取及样本构建

水电机组从结构上看由不同类型的部件构成，包括固定部件、支撑部件及转动部件，其中任一部件存在问题都可能引发机械振动。机械振动代表的频率成分主要为转频及其倍频。轴线不正引起的振动对转速不敏感，初始振动较大，而质量不平衡引起的振动则会随转速的增加而增大。在水电机组振动表现方面，健康状态下振动参数总是体现相近的表征，各个频率成分的幅值基本保持不变。当一些机械因素发生退化时，相应频率成分的能量值会有所增加，或在频谱中有新的频率成分产生。由此可知机械振动状态的退化，总体上体现在振动峰峰值的变化，细节上体现在振动频率成分能量上的变化。因此机组机械振动状态应包含振动信号总体幅值特征及频率成分细节特征两部分，如图1所示。

1.1 峰峰值趋势特征提取方法

机组转速的高低影响其机械振动幅值的大小，当机组转速发生变化时，机械振动信号的波形和能量也随之变化。在开机升转速过程前期转子没有励磁，在稳定性表现上可认为主要是机械因素的作用，为机械振动体现最为明显的工况。因此基于此过程状态监测数据分析挖掘可以获得机组在不同转速下机械振动状态表征信息。另外想要建立在线的机械振动状态实时评估模型，基于开机升转速过程获取机械振动稳定性特征也是唯一的途径。机械振动特征中峰峰值计算方法主要有文献［19-21］，图2为开机升转速过程中采用等角度间隔连续采样方式获得的机组主轴径向振动波形图。机组旋转每周采样256个点，对应采样频率为256fd（fd为机组当前转频）。在整个开机升转速阶段机组旋转了128周。对于开机升转速过程振动波形数据，若按照时段区间法，以8 个周期为一个计算区间，则只可得到16个峰峰值点，对峰峰值变化趋势特征描述不够细密。

图2 升转速过程振动波形图Fig.2 Vibration waveform during speed rising

针对机组开机升转速过程快速的特点，为更加丰富地提取振动峰峰值变化趋势特征，在相关标准及规程推荐峰峰值算法基础上，提出针对开机升转速过程的“97%置信度区间平移峰峰值”计算方法，主要步骤如下：

（1）如图3 所示，选取波形信号前8 个周期数据作为第一个计算区间，第二个计算区间为第一个计算区间沿时间方向右移一个周期，依次类推。

图3 峰峰值计算区间选取Fig.3 Selection of peak to peak calculation interval

（2）为防止可能存在的随机与干扰噪声对峰峰值计算结果的影响，对计算区间内数据加97%置信度处理。如图4所示，对计算区间内数据进行概率统计，剔除波形最小及最大各1.5%数据。

图4 计算区间波形数据概率统计Fig.4 Calculate interval data probability statistics

（3）计算第一个区间内置信度处理后波形数据最大值与最小值差值，作为第一个峰峰值。以此类推，得到开机升转速过程振动波形所有峰峰值数据。

针对图2 中包含128 个周期数据的升转速过程波形，利用“97%置信度区间平移峰峰值”计算方法则可以获得121个峰峰值数据，实现更加丰富地提取开机升转速过程振动峰峰值变化趋势特征。假设升转速过程采集的数据对应的旋转周期数为T，则利用开机升转速过程“97%置信度区间平移峰峰值”能够得到的峰峰值点数为T-7。

1.2 特征阶次频率幅值提取方法

在水电机组开机升转速过程中，机组处于变转速状态下，若仍采用等时间间隔采样的话，会出现频谱模糊现象，无法准确地获得振动特征信息。为获取升转速动态过程振动信号阶次频率特征，通过硬件阶次跟踪与阶次分析结合，构建了针对水电机组开机升转速过程的机械振动阶次频率特征提取方法，主要流程如图5 所示。在开机过程中，根据键相传感器测得的转速信息，由频率计数器及比例合成器产生与机组转速成比例的信号，一方面将其用于设定采样频率使其与转速同步，另一方面将其用于跟踪滤波器截止频率的动态设定，防止频率混叠。由此实现振动角度域平稳信号的获取，即每个机组旋转周期内获取相同的振动采样点数。

图5 基于升转速动态过程的振动特征阶次频率特征提取流程Fig.5 Vibration feature order frequency feature extraction process based on Speed-up dynamic process

在对升转速过程振动信号进行分析时，由于已通过阶次跟踪技术获得角度域平稳信号，因此可利用FFT 进行分析。分析过程中与时间域等间隔采样获得信号不同的是时间域等间隔整周期采样FFT 分析是以等时间间隔对应的频率分辨率为基准，获得幅频谱，而对于等角度采样所取信号利用FFT 进行分析是以等圆周角度对应的机组转频为基准，获得阶比幅频谱，其中阶次对应振动波动次数与机组旋转次数的比值，由此实现对升转速动态过程振动转频及其倍频的阶次特征提取。转速频率为第一阶次，相应转速下特征阶次频率为：

式中：f0(i)为第i阶频率；n为机组转速。

对于角度域平稳信号进行傅里叶分析获取其阶次幅值特征公式如下：

式中：x(kt)为实际等角度采样离散信号值；X(n/Nθ)为阶次谱上对应谱线幅值；N为信号采样点数；θ为采样角度域间隔；n为频谱离散值序号；k为时域离散值序号。

1.3 机械振动状态样本构建

稳定性状态样本作为水电机组机械振动状态评估的输入，其相关特征量的选取是否合理关系到评估的最终结果的准确性。针对机组开机升转速过程及机械振动特征，建立基于单元振动峰峰值变化趋势及多元特征阶次频率能量占比变化趋势的机械振动状态样本。

对于水电机组第i次开机过程下振动参数Xj（j=1，2，…，n），在机组升转速过程t（t=1，2，…）时刻（不同转速）采集的信号时域波形数据，构建基于单元振动峰峰值变化趋势的机组机械振动状态样本。在任一开机过程获得的振动稳定性参数Xj单元峰峰值变化趋势样本表示为：

式中：N为升转速过程振动峰峰值点数，其值等于T-7，T为升转速过程振动波形数据对应机组旋转周期数。

由此得到任一开机升转速动态过程所有振动参数单元峰峰值变化趋势整体样本表示为：

式中：i为机组某次开机序号，i=1，2，…，m。

基于升转速过程振动等角度采样信号波形数据，每个振动参数在该转速下的特征由提取的V个特征阶次频率能量占比变量描述，则开机升转速过程任一转速下振动参数Xj多元特征阶次频率能量占比样本表示为：

式中：t=1，2，…，N，表示开机动态过程某一时刻转速；j=1，2，…，n，表示不同振动参数。

由此也可得到单一振动参数在升转速过程的多元特征阶次频率能量占比变化趋势表征向量：

式中：N为升转速过程样本点数；V为稳定性参数特征变量维度，形成稳定性参数Xj在开机升转速动态过程的样本点空间。

式中：N为升转速过程样本点数；V为稳定性参数特征变量维度；i为某次开机序号，i=1，2，…，m。

2 机械振动状态评估模型

在获得水电机组机械振动总体幅值及特征频率能量占比趋势样本基础上，将数据挖掘中距离判断理论引入水电机组机械振动状态评估研究，基于计算机械振动状态健康样本与监测样本的距离来度量样本的相似度，由此实现对水电机组机械振动状态的定量评估，并建立机组机械振动状态归一化评估指标（Normalized Degradation Index of Mechanical Stability，NDIMS），状态监测样本与健康样本距离越小，NDIMS值越小，说明机组当前状态越好，反之说明机组稳定性状态发生退化，甚至故障。这样不仅可实现对水电机组机械振动状态定量评估，也可实现对机械振动状态分级评价。

2.1 模型整体结构

基于开机升转速动态过程的水电机组机械振动状态评估模型结构如图6所示，模型包括两部分：①机械振动状态样本数据；②机械振动状态跟踪评估模型。模型整体实现步骤如下：首先利用状态监测系统实现对升转速过程机组稳定性状态数据采集并存储，机组长期运行后获得大量开机升转速过程机组稳定性样本；其次，基于开机升转速过程的机械振动特征构建机械振动状态评估样本，将基于机组刚大修后稳定性表现较好时升转速过程稳定性状态监测数据分析提取的样本作为机械振动状态健康样本，机组后期运行过程中产生的样本作为机械振动状态监测样本；最后，将基于单元峰峰值变化趋势及多元特征阶次频率能量占比变化趋势的机械振动状态评估方法相结合，实现机械振动整体状态变化趋势评估。

图6 水电机组机械振动状态评估模型Fig.6 Evaluation model of mechanical vibration state of hydropower unit

2.2 基于单元峰峰值变化趋势的机械振动状态评估方法

水电机组振动峰峰值是机械振动信号特征常用的表征量，为机械信号中所有频率成分整体幅值的综合，从总体上反映了机组振动的剧烈程度。因此采用稳定性参数峰峰值作为特征变量，提取开机升转速过程峰峰值变化趋势特征，将数据挖掘中距离评判理论引入机组机械振动健康状态评估中，提出了一种基于单元峰峰值变化趋势及欧氏距离的水电机组机械振动状态评估方法。实现流程如下：

步骤1：利用97%置信度区间平移峰峰值计算方法，计算得到机械振动状态单元峰峰值变化趋势样本。如式（8）及（9）所示，将利用机组大修后初期数据分析获得的机械振动状态健康样本表示为X0，机组后期历次开机运行过程中提取的机械振动状态监测样本表示为Xi。为衡量同一转速下机组稳定性表现，对健康样本及监测样本数据起点及终点进行统一处理，分析数据起点统一为50%转速，终点为额定转速，由此实现对相同工况区间内机械振动稳定性表现对比分析。

式中：i为机组某次开机序号，i=1，2，…，m。

步骤2：基于单元峰峰值变化趋势数据挖掘的水电机组机械振动状态评估方法中，由于特征参数只有峰峰值，不存在量纲差异对评估结果引起较大影响的问题，因此直接计算机械振动健康样本与实时监测样本的平均欧氏距离，公式如（10）所示，欧氏距离计算示意如图7所示。

图7 基于单元峰峰值变化趋势的欧氏距离计算Fig.7 Calculation of Euclidean distance based on variation trend of ptp

步骤3：基于机械振动健康样本与x轴平均欧氏距离（机械振动升转速过程平均能量），将步骤2得到的机械振动状态监测样本与健康样本的平均欧氏距离值归一化处理，得到第i次开机过程基于单元峰峰值数据挖掘的机械振动状态指标值NDIMSptp(i)，如式（11）所示。依次计算机组每次开机机械振动状态指标，实现对机组长期运行过程机械振动状态变化趋势监测评估。

2.3 基于多元特征频率能量占比变化趋势的机械振动状态评估方法

基于多元特征频率能量占比变化趋势的水电机组机械振动状态评估方法，具体实现步骤如下：

步骤1：基于阶次跟踪获得的开机升转速过程稳定性参数角度域平稳信号波形数据，利用升转速信号阶次分析方法对各个转速下振动波形数据进行分析得到各个特征频率成分能量值，分别计算1/4fn～1/3fn（开机过程水力不稳定），1fn（转子不平衡或角度不对中特征），2fn（转子裂纹或平行不对中），3fn（转子碰磨），8fn（轴瓦数倍频），13fn（转轮叶片数倍频），24fn倍频（导叶叶片数倍频），>24fn（卡门涡等高频）特征频率成分能量，并基于当前转速下信号总能量进行归一化处理，将计算结果作为机组机械振动多元特征，分别用v1～v8表示。由此针对某一振动测点数据，分析获取的机械振动状态健康样本矩阵X0及监测样本矩阵Xi如式（12）及式（13）所示：

式中：g表示特征变量编号。

步骤3：对机械振动状态监测样本矩阵与健康样本矩阵中所有特征变量平均欧氏距离进行计算，并取其期望值，得到基于多元特征频率能量占比变化趋势的机械振动状态指标值NDIMSmul(i)。在机组运行一段时间后，若开机升转速过程机械振动监测样本频率成分能量结构基本无变化，则与机械振动状态健康样本距离较小；若频率成分能量结构发生明显变化，则会在样本整体距离中有所体现。由此实现考虑多元频率结构特征的机械振动状态评估。

3 实测数据验证

将提出的基于开机过程数据挖掘的水电机组机械振动状态评估模型应用于某水电站机组稳定性状态评估中。电站4号机组在2018 年3 月6 日完成了A 级检修，对水轮机转轮及发电机等进行了更换，机组容量从50 MW 增至55 MW。基于此机组2018 年3 月至2019 年2 月开机过程稳定性状态监测数据，验证所提出的方法的有效性及实用性。

3.1 基于单元峰峰值变化趋势的机械振动状态评估

根据稳定性状态监测数据库数据存储情况，剔除其中因传感器损坏等因素造成的异常数据，得到可供分析开机升转速过程稳定性状态监测样本总计88 个。各个月样本数量如表1 所示。下文将以下导X向主轴径向振动（下导X向摆度）状态进行评估研究的步骤及结果为例进行展示。

表1 机组大修后各个月样本个数Tab.1 Number of samples in each month after unit overhaul

分别计算机组在大修后每次开机升转速过程中下导X向摆度峰峰值变化趋势，获得该过程机组下导X向振动状态单元峰峰值变化趋势特征样本。经分析发现在升转速过程中每个样本趋势类似，但在幅值上有差异，即体现出振动能量的不同，以3 月份15 个样本及5 月份两个样本分析结果为例进行展示，如图8所示。其中图8（a）中黑色实线为3月份前7个样本，红色实线为3 月份后8 个样本。可以看出在升转速过程机组下导X向摆度幅值从140 μm 左右上升到250 μm。在机组刚检修完时，峰峰值变化趋势比较接近。但3月份最后两个样本在升转速中部时峰峰值明显较大，比3 月份前7 个样本大了约70 μm 左右。图8（b）为5月份样本，5月份机组两次开机过程下导X向摆度幅值150 μm 上升到340 μm 左右，5月份与3月份对比可以看出摆度最大幅值增加了接近100 μm，值得进一步关注。

图8 下导X向摆度单元峰峰值变化趋势特征样本Fig.8 Characteristic sample of PtP variation trend of lower guide X-direction swing

以电站大修后机组稳定性状态较好的前3次开机升转速动态过程监测样本的均值作为机组此测点机械振动状态健康样本。如图9所示，图9中黑线为前3次开机升转速过程下导X向摆度峰峰值变化趋势，红线为此测点振动状态健康样本。除此3 个样本之外的85 个样本作为此测点机械振动状态监测样本。分别计算机械振动状态监测样本与健康样本平均欧氏距离，并利用健康样本与X轴平均欧氏距离（代表升转速过程健康样本振动能量平均水平）进行归一化处理，得到各次开机过程基于单元峰峰值数据挖掘的机械振动状态指标NDIMSptp。依次计算机组每次开机对应的机械振动状态指标，实现对机组长期运行过程机械振动状态变化趋势监测评估。

图9 机械振动状态健康样本Fig.9 Mechanical vibration state health sample

4 号机组大修后NDIMSptp值变化趋势如图10 所示。从图10 中可以看出在3 月份机组刚大修完时，此测点机械振动状态较好。3 月之后机械振动状态指标值有增大趋势，最大值达到0.48，状态指标值增大可能与此阶段机组运行水头偏离额定水头程度逐渐增加有关。在8 月到11 月机组运行水头较平稳，状态指标NDIMSptp值略呈下降趋势，在1 月至2 月稳定在0.2 左右。可以看出，基于单元峰峰值的水电机组机械振动状态评估方法，实现了对机组长期运行过程机械振动状态变化趋势监测评估，对掌握机组稳定性状态及了解机组稳定性状态的变化趋势方面有较好的效果。

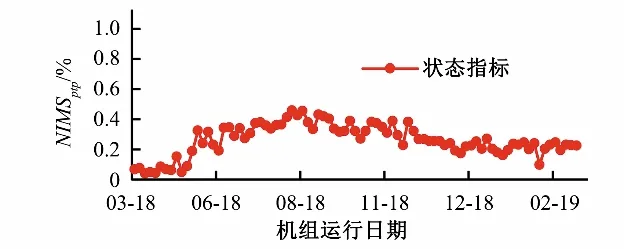
图10 机械振动状态变化趋势评估结果Fig.10 Evaluation results of change trend of mechanical vibration state

3.2 基于多元特征频率能量占比变化趋势的机械振动状态评估

基于相同样本，验证基于多元特征频率能量占比变化趋势的水电机组机械振动状态评估方法的有效性和实用性。

选取机组大修后第1次开机升转速过程状态监测数据分析得到的机械振动多元特征阶次频率能量占比变化趋势样本作为健康样本。提取机组运行历程后87 次能量占比变化趋势样本，作为此测点机械振动状态监测样本，形成机械振动状态矩阵。分别计算每个机械振动状态监测样本与机械振动状态健康样本中特征频率变量v1～v8平均欧氏距离，并取其期望值，得到基于多元特征频率能量占比变化趋势的机械振动状态指标值NDIMSmul。

对机组大修后机械振动状态样本矩阵中各个特征频率变量单独计算得到的机械振动多元评估指标变化趋势如图11 所示。从图11 中可以看出，整体上一倍频状态指标值波动最大，低频成分波动次之，其他频率成分幅值波动较小。机械振动低频评估指标在2018 年6 月份及2019 年2 月份左右幅值波动较大，机械振动状态1 倍频评估指标变化趋势与基于单元峰峰值的机组机械振动状态评估结果变化趋势类似，说明了引起峰峰值变化的主要原因是1倍频。转频及其以上频率成分状态指标在机组运行过程中比较平稳，说明在机组运行中没有异常振动频率成分出现。

图11 机械振动状态变化趋势（特征频率）Fig.11 Variation trend of mechanical vibration state（characteristic frequency）

计算得到各个机械振动状态监测样本基于多元特征频率能量占比变化趋势的水电机组机械振动状态评估综合指标值，结果如图12 所示。可以看出按照基于多元频率能量归一化占比数据分析得到的机械振动综合评估指标来看，长期运行历程中机械振动状态表现相对平稳，频谱能量分布结构较为稳定。整体分析结果表明机械振动状态在频谱能量分布结构方面没有明显异常发生，机械振动状态较好。

图12 基于多元频率特征的状态指标变化趋势Fig.12 Change trend of state index based on multivariate frequency characteristics

4 结论

本文提出了基于开机变转速过程单元峰峰值变化趋势及多元特征频率能量占比变化趋势的水电机组机械振动状态评估方法。

结合某电厂4号机组大修以来机械振动状态变化趋势进行了实际应用，分析结果表明该方法可以有效地评估机组在大修后运行历程中机械振动状态，在量化水电机组机械振动状态变化趋势方面具有良好的效果和实用性，实现了在机组开机早期发现可能存在的安全隐患，保障机组的安全稳定运行。