考虑不同服装热阻的层式通风供暖运行优化研究

白 燕，汪庭祥，申一凡

(1.西安建筑科技大学 信息与控制工程学院，西安 710055；2.西安建筑科技大学 理学院，西安 710055)

0 引言

如今，人们80%～90%的时间在室内度过，近65%的时间在办公楼里度过[1]，室内人员的工作效率很大程度上取决于他们对室内环境的满意度[2]。一直以来，气流组织对营造舒适健康的室内环境起着至关重要的作用。合理的气流组织不仅可以为室内人员提供舒适的热环境，还可以降低空调系统的能耗以及改善室内空气质量[3]。因此，在过去的几十年中，许多研究学者致力于一系列关于新型气流组织形式的研究，例如个性化通风[4]、碰撞射流通风[5]和竖壁贴附通风[6]等。

层式通风是一种适用于中小房间的新型气流组织形式，其最初提出是为了适应供冷工况中较高的室内空气温度[7]，因此以往关于层式通风的研究主要集中在夏季供冷工况。有研究表明，对于供冷工况，与混合通风和置换通风相比，层式通风能够以较低的能耗营造令人满意的室内热环境[8]。近年来，层式通风用于冬季供暖已被证实具有一定的潜力。由于受到热浮力的影响，层式通风供暖工况下的气流流动显得更为复杂[9]。因此，合理的控制供暖送风参数对于营造舒适的室内热环境和降低能耗至关重要。Zhang等采用数值模拟分析不同送风参数对层式通风供暖的通风性能的影响，发现送风温度对热舒适性的影响最显著，送风角度对能量利用效率的影响程度最显著，送风速度对空气质量的影响最显著[9]。程勇等采用数值模拟研究分析不同送风角度对层式通风供暖效果的影响，发现水平向下30° 送风角度可获得较好的室内热舒适和较高的能量利用效率[10]。

在以往对于气流组织形式的研究中，常使用静态服装模型(即将服装保温设置为固定值)来评估操作参数对通风性能的影响[9,11]。该值参考了美国[12]，欧洲[13]和国际[14]热舒适性标准，即供冷季节和供暖季节的服装热阻分别为0.5 clo和1 clo。根据标准ASHRAE 55-2013，服装隔热是影响居住者热舒适度的重要因素之一(其他因素包括：空气温度，空气速度，相对湿度，平均辐射温度和代谢活动)[12]。基于人体热平衡，较低的室内温度会导致人体消耗更多的热量，这让人感觉到寒冷从而选择添加衣服来维持自身的热平衡。有研究表明，在冬季时，中国的室内温度低于欧美国家，中国人的室内服装热阻高于欧美人群，且范围最广[15]。因此，若服装热阻设为固定值而不考虑室内人员的实际服装热阻，则很有可能导致送风参数设置不合理。

本研究基于实验数据验证的CFD数值模拟，以PMV、垂直温差、空气龄以及能量利用效率为优化目标，在考虑不同服装热阻的前提下，通过改进逼近理想解排序(TOPSIS)法对送风参数进行优化。在优化过程中，本研究采用中心复合设计响应面法得到通风性能与设计参数间的函数关系并用于送风方案评估，显著地降低数值模拟的计算成本，同时可为层式通风供暖工程设计提供指导。

1 数值模拟

1.1 物理模型

本研究是以西安地区某一典型的办公室为基础物理模型，房间尺寸为长4.1 m(X)×宽3.2 m(Z)×高2.7 m(Y)，如图1所示。

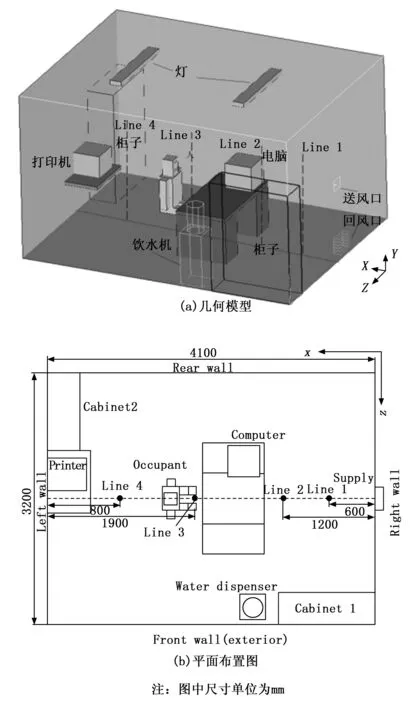
图1 实验环境几何模型和平面布置图

房间的前墙为外墙，其余的墙面、地面和屋面均为内墙，在数值模拟过程中内墙可以设置为绝热壁面[9-10]。为简化计算模型和提高计算网格质量，使用接近人体实际形状的矩形节段模型来代替复杂的人体[16]。一个百叶送风口安装在右墙上，距离地面高约1.3 m，尺寸为：长0.25 m×高0.25 m，送风角度可以通过改变百叶的角度进行调节。回风口位于送风口正下方，距离地面约0.2 m，其尺寸为：长0.3 m×高0.3 m。经过加热的暖风通过送风口直接输送至工作区，待其与室内较冷空气混合后，再经过回风口排出。房间共布置4条测量线(Line 1～Line 4)用于数据采集，分别在水平方向上距离送风口中心位置0.6 m、1.2 m、2.2 m和3.3 m。

1.2 CFD模型

为了简化模型方便计算，本研究做以下基本假设：

1)室内空气为不可压缩、稳定的湍流气流且满足Boussinesq假设；

2)房间为密闭空间，无其他气流的渗透；

3)房间外墙温度为常壁温。

除此之外，采用Discrete Ordinates(DO)辐射模型来计算不同表面(外墙、人体表面、灯、电脑、打印机等)之间的热传递。文献[11]表明标准k-ε两方程湍流模型能够更好的预测通风空调房间的空气流动。因此，本研究采用标准k-ε两方程湍流模型。本研究使用Airpak 3.0.16建立层式通风空调房间的几何模型，如图1(a)所示。为了保证数值模拟预测结果的精度，本研究采用六面体结构化网格对模型进行网格划分，并对送风口、排风口、人体、电脑等处进行局部网格加密处理。使用有限体积法线性化微分方程组，其中，标准压力项、动量项、湍流能项、湍流耗散项均为二阶格式。采用SIMPLE-C算法耦合速度和压力。能量和空气龄收敛残差设置为10-6，其余参数收敛残差均设置为10-4。

1.3 初始条件和边界条件

在CFD数值模拟中，边界条件设置详情如表1所示。

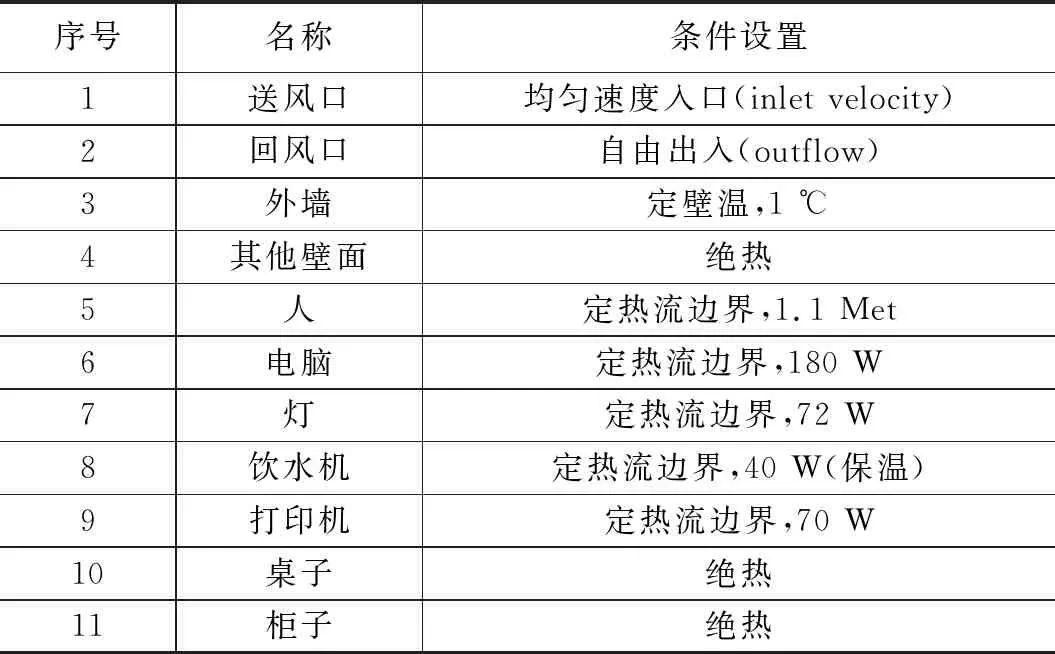
表1 数值模拟边界条件设置

1.4 网格独立性检验

为了确定CFD仿真模型的网格数量，本研究对网格数量为354 756(网格1)、567 998(网格2)和956 712(网格3)的3种网格进行网格独立性检验。对以上3种网格进行数值模拟，在Line 1(X=0.6 m，Z=1.6 m)的空气速度和温度的数值模拟预测值如图2所示。通过比较可以看出，网格2的空气速度和温度的数值模拟预测值与网格3非常接近，而网格1的空气温度预测值和网格3的温度预测值存在较大偏差。一般来说，网格划分越精细，网格密度就越大，数值仿真结果与流场的实际情况越接近。然而网格密度过大会造成数值计算的迭代次数的快速增加，从而导致数值模拟的时间成本大大增加[17]。考虑到数值模拟的预测精度和时间成本，本研究选择采用网格2。

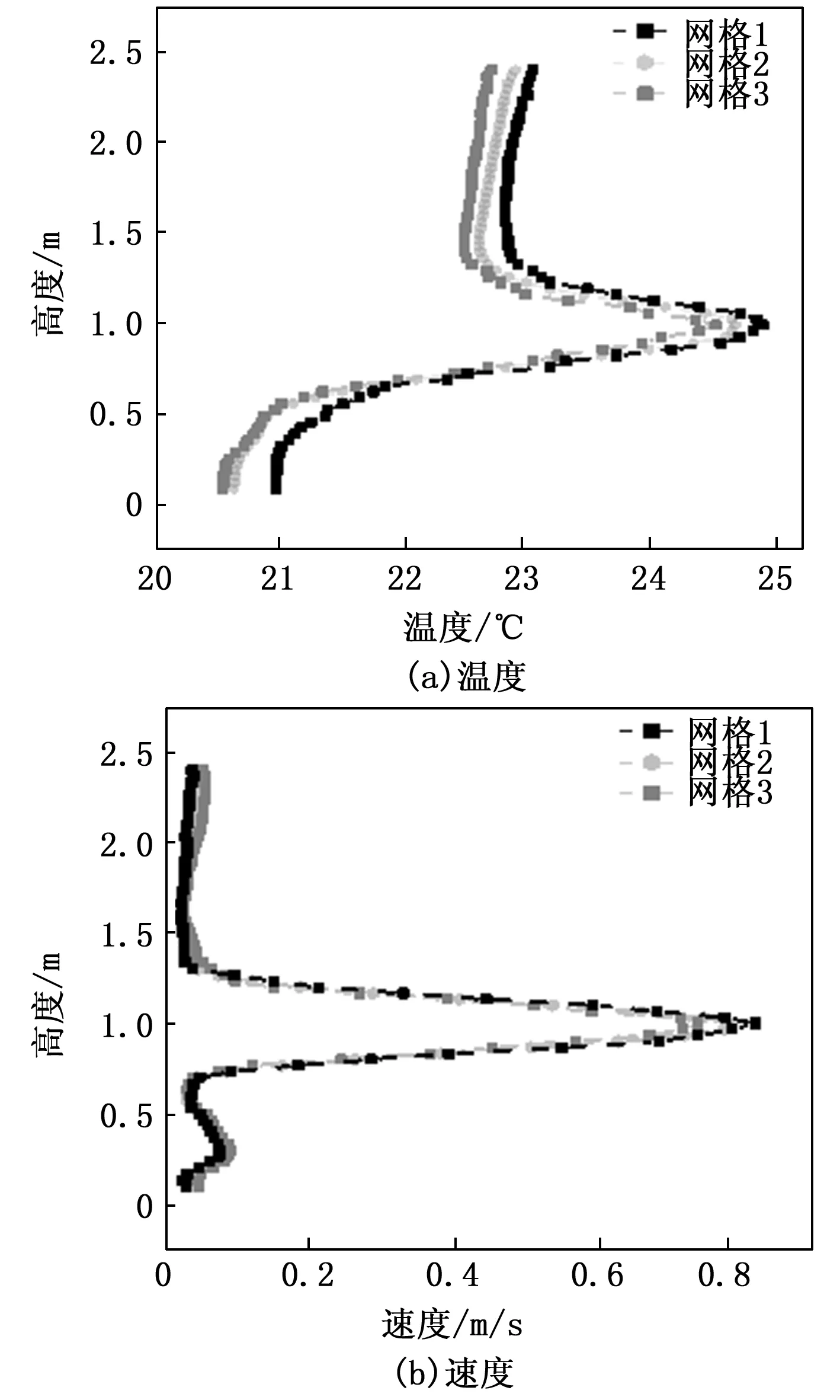
图2 网格独立性检验

1.5 数值模拟的验证

为了确保数值模拟方法的可靠性，本研究对CFD模型进行实验对比验证。在房间设置了一面内墙，并在该墙上安装层式通风的送风口和回风口，且风口的位置、尺寸与CFD模型保持一致，如图3所示。

图3 通风系统的风口设置

本研究在4条测量线上距离地面0.3 m、0.5 m、0.7 m、0.9 m、1.1 m、1.3 m、1.5 m、1.7 m和2.1 m高度处设置测点。在采集实验数据时，采用风速仪测量各个测点处的空气速度，采用温湿度变送器测量各个测点处的空气温度，采用K型热电偶测量围护结构的表面温度，仪器及参数详情如表2所示。每个测点的数据采集时长为5 min，间隔10 min逐一完成每个测量线上所有测点的空气温度和速度的数据采集。为防止实验仪器的测量结果出现系统误差，在实验测量开始前，采用参数对比的方法对仪器进行检查，若仪器出现误差，则对其进行参数校准。

表2 实验仪器具体参数

图4为实验测量结果与模拟预测结果的对比，由图可知数值模拟预测值与实验测量值的大小相近、变化规律基本一致。为评估数值模拟的准确性，本研究采用平均绝对误差(MAE)和均方根误差(RMSE)对所有测点处的数值模拟值与实验测量值进行误差分析。经计算，所有测点的空气温度数值模拟值与实验测量值之间的MAE与RSME分别为0.21 ℃和0.22 ℃，空气速度的数值模拟值与实验测量值之间的MAE与RSME分别为0.03 m/s和0.04 m/s，表明数值模拟预测结果具有一定的准确性。因此，该CFD数值模拟可以较好地模拟层式通风供暖工况。

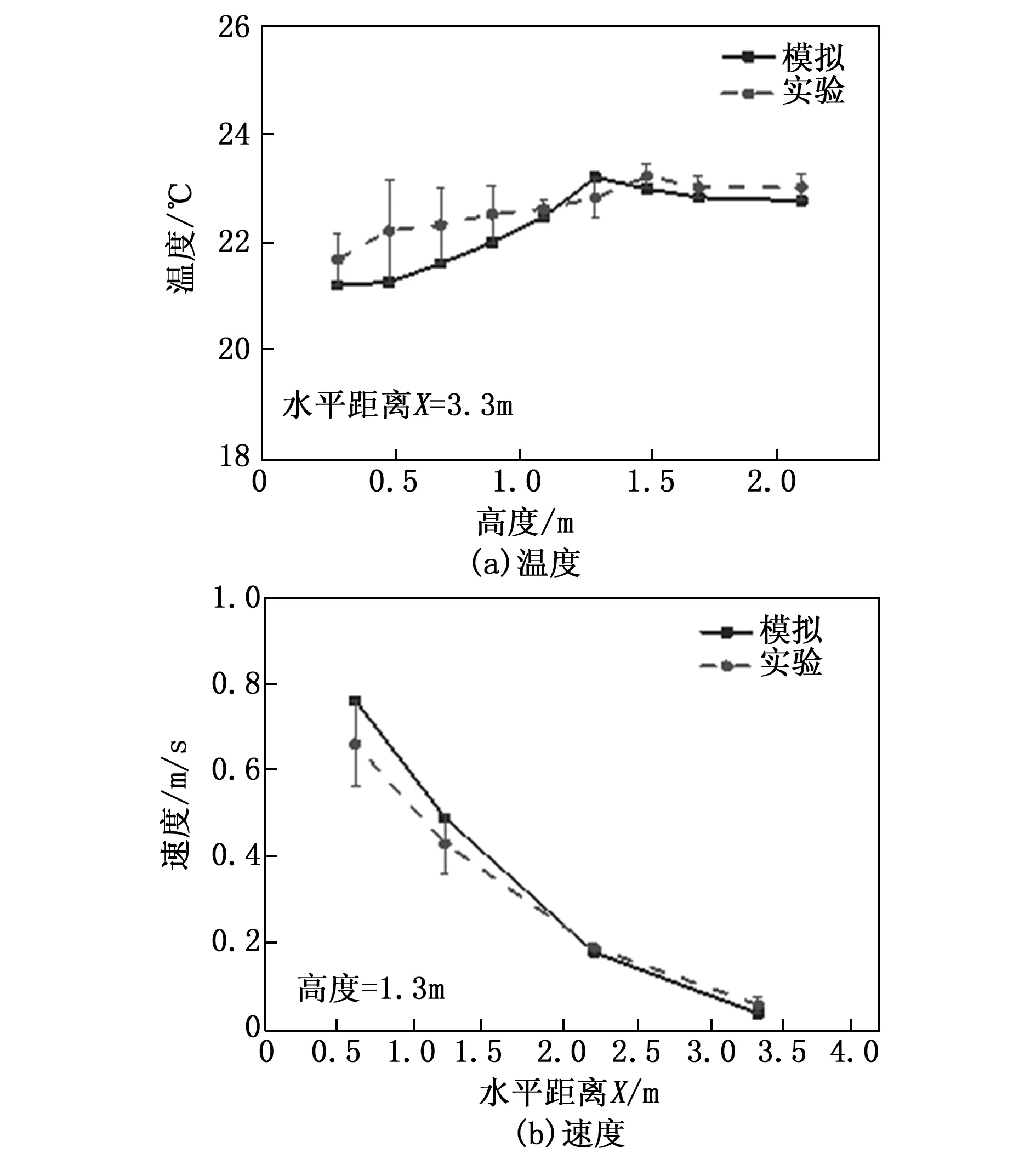
图4 比较实验测量与数值模拟的空气温度和速度

2 研究方法

2.1 通风性能评价指标

本研究采用以下评价指标对层式通风的能量利用效率、空气质量和热舒适进行评价。

1)能量利用效率(EUC)；

2)空气龄(MAA)；

3)垂直温差(ΔT)；

4)预测平均热感觉投票/预测不满意百分比(PMV/PPD)。

能量利用效率(EUC)用来评估层式通风输送至房间的暖风热量的利用效率[18]。由于本模型中的人体为坐姿，因此工作区主要包括距离地面1.3 m高度以下的区域[11]。EUC数值越大，则说明送往室内工作区的暖风得到充分利用。其计算公式为[18]：

(1)

式中，EUC代表能量利用效率，Te为排风温度(℃)，Ts为送风温度(℃)，Tn为工作区空气平均温度(℃)。

空气龄(MAA)为室内空气质量的评价指标，其定义为室内保留一定数量的新鲜空气的时间长度[19]。本研究的MAA值在人员呼吸高度(距离地面以上1.1 m)取得[20]。预测平均热感觉投票/预测不满意百分比(PMV/PPD)为全身热舒适的评价指标。由于相对湿度的变化对热感的影响很小，因此可以忽略不计[21]。在计算PMV/PPD时，将相对湿度设置为50%，活动水平设置为1.1 Met[11]。垂直温差(ΔT)为局部热舒适的评价指标，其值为室内人员的头部(距离地面以上1.1 m)和脚踝部(距离地面以上0.1 m)两处的空气温度之差。

2.2 改进TOPSIS法

本研究采用的通风性能评价指标涉及热舒适、空气品质和能量利用效率3个方面，彼此之间可能存在矛盾，即某个送风方案会使得一项评价指标变好，却使得另一项指标变差。因此，改善多个通风性能评价指标可看作为多目标决策问题。TOPSIS法是解决该问题的一种常用的方法，其原理是根据现有的方案与理想目标的接近程度按照优劣进行统一的排序[22]，评估现有方案并筛选出最佳方案。然而，TOPSIS法存在不可忽视的不足之处：与正理想解的欧式距离接近的方案很有可能也与负理想解的欧式距离接近[23]。为了解决这一问题，本研究使用集对分析中的联系向量距离对TOPSIS法进行改进。由于考虑对立集合的存在，因此在计算方案与理想解的联系度时，将会在一定程度上克服TOPSIS法的不足之处，从而具有了“与正理想解的联系向量距离更近，与负理想解的联系向量距离更远的方案”的性质[24]。

假设方案A={A1，A2，…，Am}由m个方案组成，评价指标C={C1，C2，…，Cn}由n个指标组成，xij为方案Ai在指标Cj下的指标值(i=1，2，…，m；j=1，2，…，n)，则改进TOPSIS方法的计算过程如下：

1)构造初始数据矩阵X。

(2)

式中，xij为方案Ai在指标Cj下的指标值。

2)初始数据矩阵正向化。

对于区间型(在某个区间内最优)指标：

(3)

M=max{a-min{xi},max{xi}-b}

对于极小型(数值越小越优)指标：

(4)

对于中间型(越接近某个值越优)指标：

M=max{|xi-xbest|}

(5)

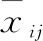
3)正向化矩阵归一化。

i=1,2,3,…m;j=1,2,3,…n

(6)

式中，yij为方案Ai在指标Cj下规范化后的评价指标值。

4)构建权重矩阵。

fj=1-Mj

(7)

式中，Mj为指标Cj的信息熵；fj为指标Cj的信息离散度；λj为指标Cj的权重。

5)构建加权归一化矩阵。

zij=λjyij,i=1,2,3,…，m;j=1,2,3,…，n

(8)

式中，zij为方案Ai在指标Cj下的指标值加权后的归一化数据。

6)确定正理想解Z+和负理想解Z-。

正(负)理想解是由加权归一化矩阵中每一列的最优(劣)值组成：

Z+={zi1max,zi2max,zi3max,…,zinmax}

(9)

Z-={zi1min,zi2min,zi3min,…,zinmin}

(10)

7)计算方案Ai与正理想解Z+和负理想解Z-的联系度。

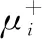
(11)

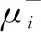
(12)

式中，ai,bi和ci依次分别为方案Ai和理想解Z的同一度、差异度和对立度[24]，ai+bi+ci=1；p是差异相应系数，在[-1, 1]区间视不同情况取值；q是对立相应系数，其取值为-1[24]；μij为方案Ai的指标Cj与理想解Z的联系度。

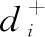
(13)

(14)

9)计算方案Ai与理想解的相对贴近度。

(15)

相对贴近度Ci越大，则说明方案Ai就越接近于理想解。因此，本研究通过计算各送风方案的相对贴近度并根据大小进行优劣排序，其中，最接近1的方案就是最佳方案。

2.3 响应面法试验设计

一般来说，现有的送风方案数量越多，基于改进TOPSIS法就越可能选出更加合理的最佳送风参数。然而送风方案数量的增加势必导致CFD数值模拟的时间成本增加[11]，因此有必要建立通风性能的近似数学模型来代替CFD数值模拟，用于通风性能评价指标的分析与预测。响应面法(RSM，response surface methodology)作为一种常用的数学建模方法，其采用二次回归方程，通过最小二乘回归法确定设计变量与输出响应之间的映射关系[25]，具有计算精度高、预测性能好的优点[26]。为构建通风性能响应面模型，首先要选择合适的试验设计方法，进行试验设计与模型检验，从而构建出通风性能响应面模型。响应面试验设计方法有很多种，如Box-Behnken试验设计、中心复合试验设计(CCD，central composite design)和Hybrid试验设计等[27]。由于CCD试验设计具有合适的轴点坐标，能够保证试验设计的可旋转性和序贯性，并且能够在等距点上预测恒定方差和改善预测精度[28]，因此本研究采用CCD试验设计。

本研究选取送风角度(A)、送风速度(B)、送风温度(C)以及服装热阻(D)作为CCD试验的设计变量。其中送风角度、送风速度和送风温度的参数范围分别为0～60 °、0.6～1.2 m/s和22～28 ℃，服装热阻的参数范围为0.8～1.4 clo，以表示室内人员在冬季供暖时的不同的着装。为保证CCD试验设计的可旋转性和序贯性，本研究的轴向点极值(α)的取值需遵循α=2t/4(t为变量数目)，在每个变量的参数范围内选择5个不同值进行试验，变量实际值与水平编码值对应情况如表3所示。

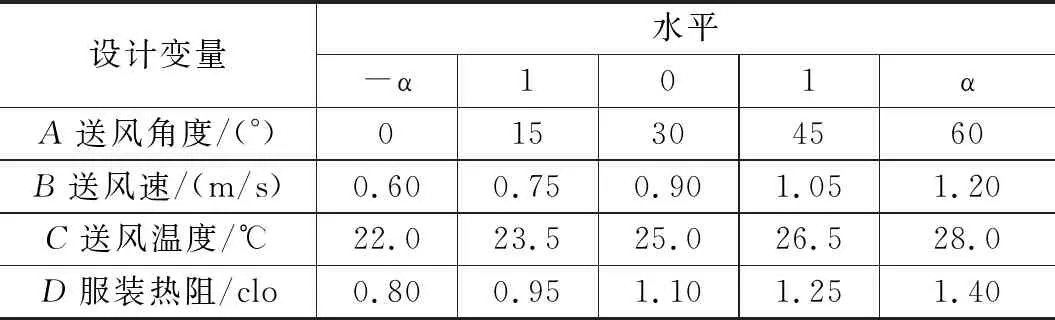
表3 CCD试验变量、水平及实际值

基于表3中不同设计变量与水平，根据CCD试验设计形成30组试验工况，以PMV、ΔT、MAA和EUC为输出响应，按照不同试验工况分别进行数值模拟，结果如表4所示。

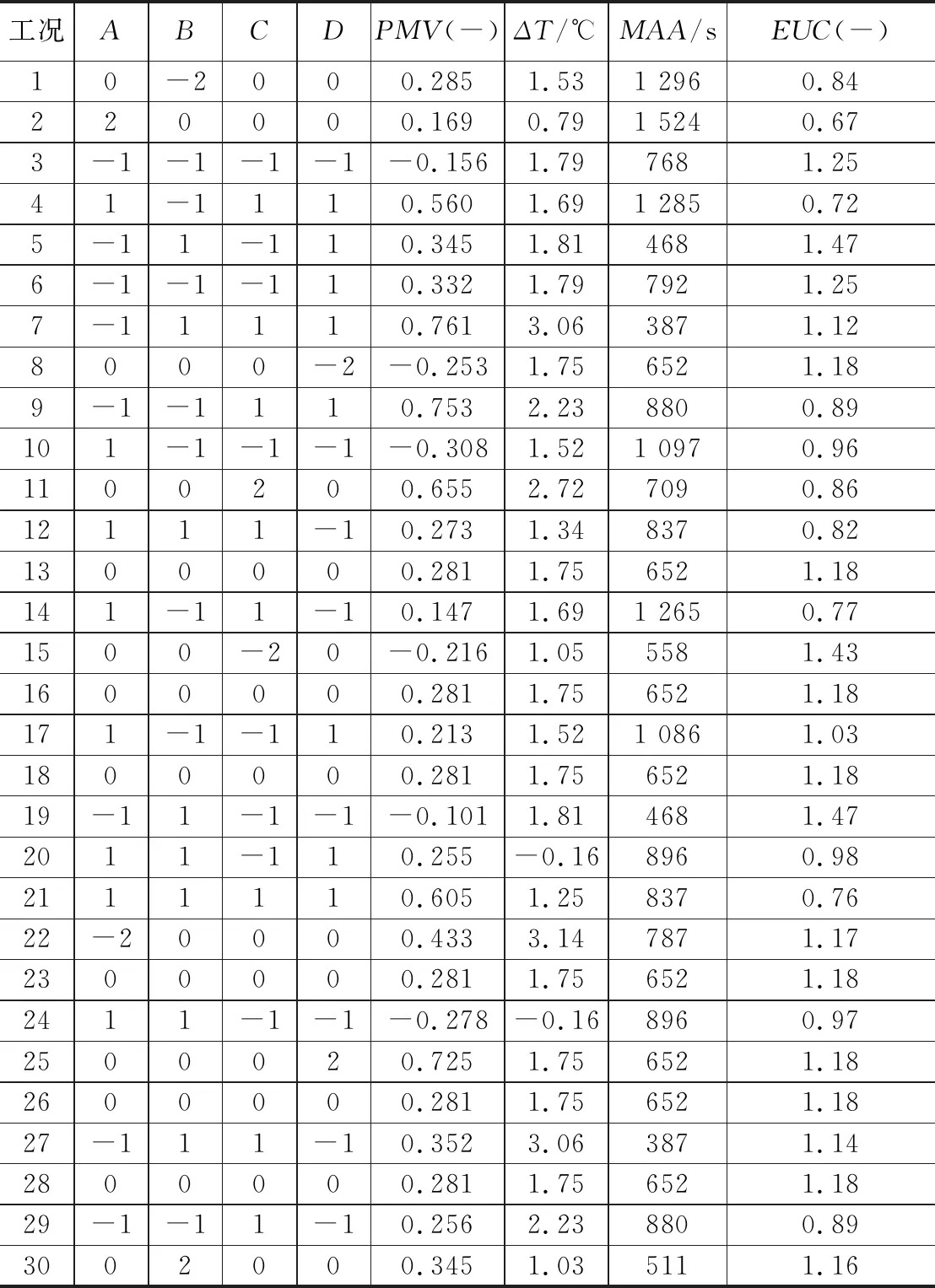
表4 试验工况及模拟结果

3 结果与分析

3.1 通风性能的响应面模型

考虑到所有线性项、平方项和设计变量间的交互作用[28]，本研究采用二阶多项式模型构建通风性能与设计变量之间的函数关系。二阶多项式模型的数学表达式如式(16)所示:

(16)

式中,n为设计变量的数量；y为预测的响应值；c0、cr、crr分别为偏移项、线性项和平方项系数；crs为交互作用系数。

为确定设计变量与输出响应的映射关系，本研究在构建响应面模型过程中，采用二次多项式逐步回归—后退法，剔除显著性较小的项，以提高模型的稳定性与准确性。根据表4的30组数值模拟结果，利用Design-Expert 12软件[30]对进行回归拟合，通过式(16)获得PMV、ΔT、MAA和EUC的响应面模型，如式(17)～(20)所示:

PMV=-13.723-4.453×10-3A+0.149B+0.673C+

5.371D-9.361×10-2CD-8.545×10-3C2-0.671D2

(17)

ΔT=15.986+9.293×10-2A-17.726B-0.813C-

0.157AB+1.217BC-1.8×10-4A2-4.979B2

(18)

MAA=-893.28-43.741A-662.29B+210.53C+

9.53AB+0.586AC-235.278BC+0.557A2+

2768.403B2

(19)

EUC=-1.82-6.194×10-3A+5.122B+0.153C-

2.417×10-2AB+1.472×10-3AC-3.08×10-4A2-

2.194B2-5.833×10-3C2

(20)

式中，A为送风角度(°)；B为送风速度(m/s)；C为送风温度(℃)；D为服装热阻(clo)。

图5为CFD数值模拟值与响应面(RSM)模型预测值的分布，横轴为CFD数值模拟值，纵轴为RSM模型预测值。由图可以看出，响应面(RSM)模型预测值与CFD数值模拟值基本一致，绝大部分数据点都分布在直线y=x上。说明了建立的通风性能响应面模型较为精确有效。

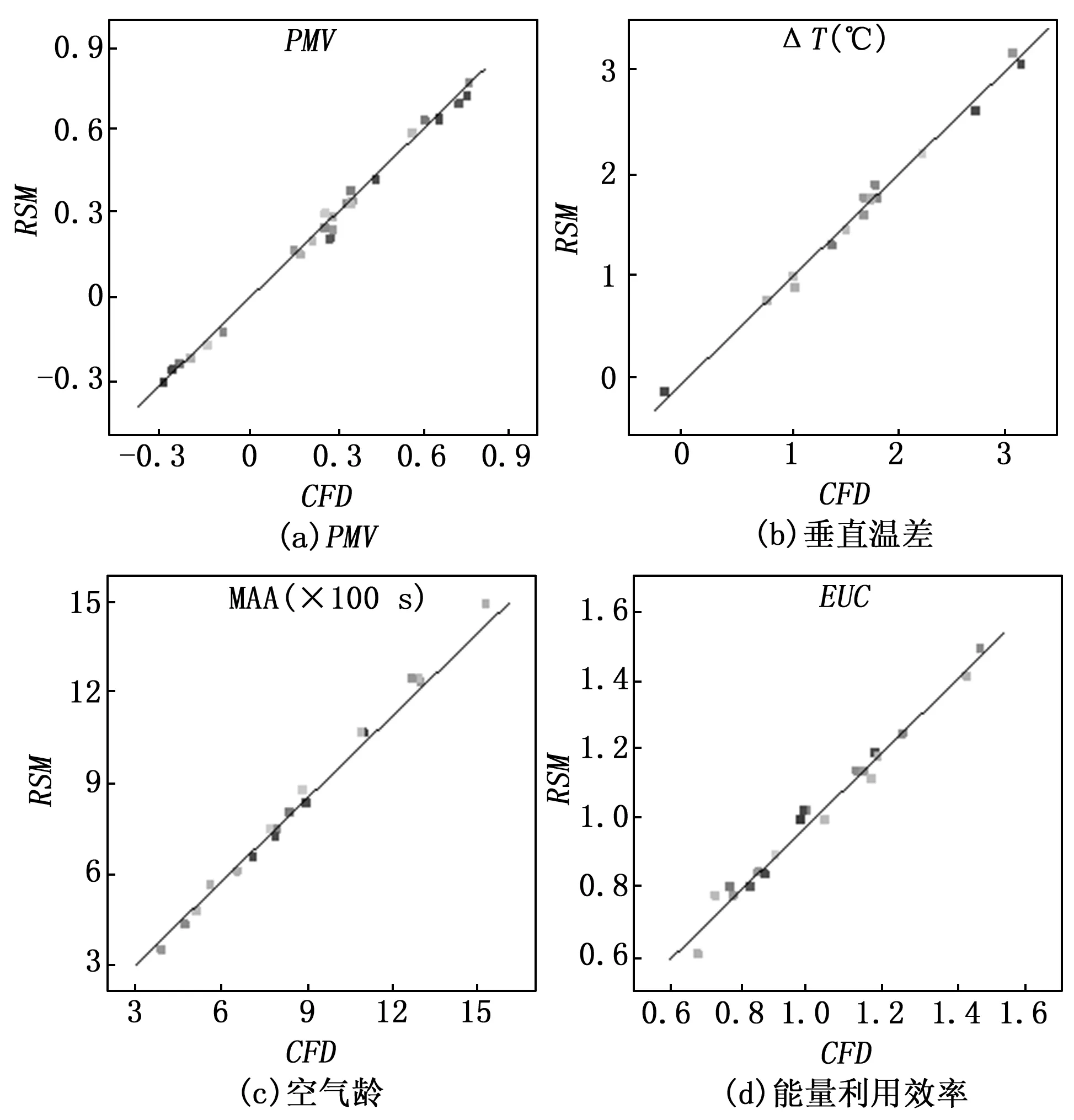
图5 RSM模型预测值与CFD数值模拟值分布图

对以上通风性能响应面模型进行方差分析，以确认模型能否有效地反映输出响应与设计变量的映射关系。如表5所示，4个模型的p值均小于0.000 1，表明模型在统计学上具有重要意义。

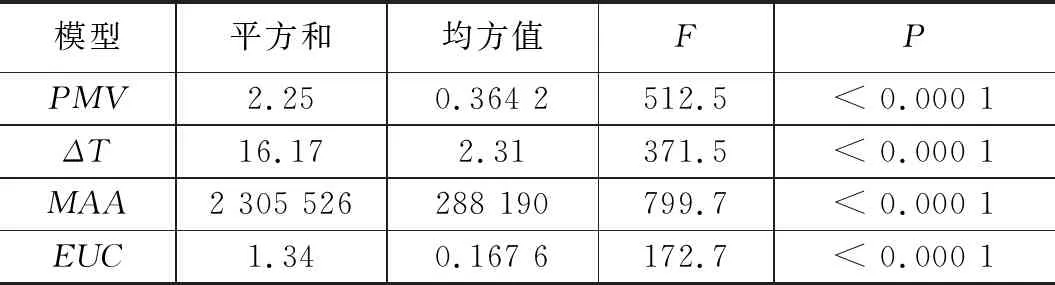
表5 模型方差分析

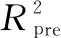
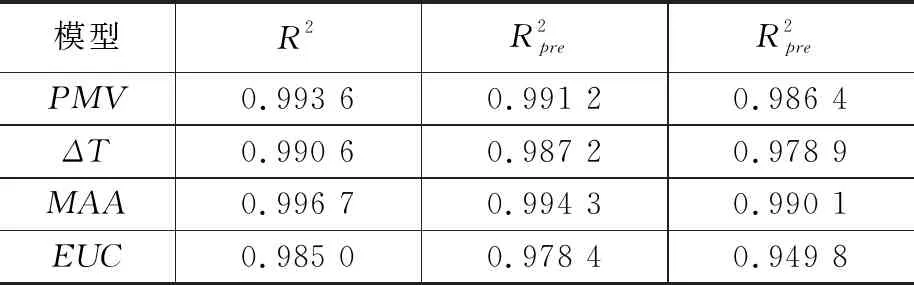
表6 模型决定系数分析

基于构建的通风性能响应面模型，通过改变4个变量中的1个变量的编码值，得到各通风性能评价指标与变量水平编码值的对应关系，结果如图6所示。图中各变量的斜率陡峭程度可反映出该变量对输出响应的影响程度，斜率越陡则表明影响程度越大。

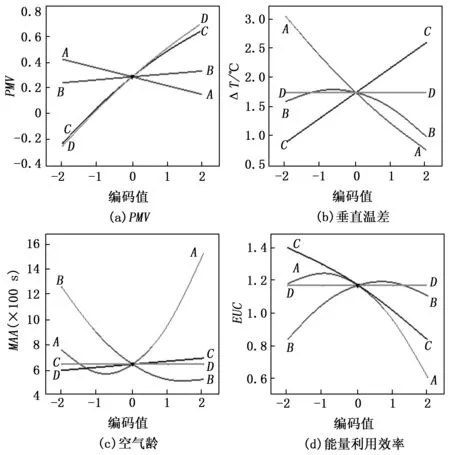
图6 通风性能与变量编码值关系

由图6(a)可知，在4个变量中，服装热阻(D)斜率最陡，然后是送风温度(C)、送风角度(A)和送风速度(B)，说明对PMV的影响程度从大到小为：服装热阻、送风温度、送风角度和送风速度，因此有必要针对室内人员在不同着装的情况下进行送风参数优化。同理，由图6(b)可知，4个变量对ΔT的影响程度从大到小为：送风角度、送风温度、送风速度和服装热阻；由图6(c)可知，4个变量对MAA的影响程度从大到小为：送风角度、送风速度、送风温度和服装热阻；由图6(d)可知，4个变量对EUC的影响程度从大到小为：送风角度、送风温度、送风速度和服装热阻。此外，由图6可以看出，各项通风性能指标随着设计变量并非呈现单调一致性变化。因此，在对层式通风供暖进行优化时，需要考虑各变量对通风性能的综合影响，使层式通风供暖的综合性能达到最佳状态。

3.2 基于改进TOPSIS的通风性能多目标优化

本研究总共考虑了6 859种送风方案，由19种送风温度、19种送风速度和19种送风角度组成，分别在相应的参数设计范围内等间隔设置。同时，在参数的设计范围内等间隔地设置13种服装热阻，用以研究室内人员着装情况对送风参数优化的影响。每个送风方案的通风性能评价指标可由式(17)～(20)计算得到。若没有响应面模型，则需要进行6 859次CFD数值模拟，意味着需要花费大量的时间来完成这项工作，而本研究仅进行30组实验方案的CFD数值模拟，因此通风性能响应面模型的建立，可以在节约计算成本的同时，较为精准预测各送风方案的通风性能。

在优化过程中，根据式(7)可计算出各项通风性能评价指标的权重，经计算PMV、ΔT、MAA和EUC的平均权重分别为0.392、0.235、0.207和0.166，表明室内热舒适是进行送风参数优化时最重要的指标。基于建立的通风性能响应面模型，采用改进的TOPSIS法可得到针对不同服装热阻的最佳送风参数。以服装热阻为0.8 clo为例，利用改进TOPSIS法可得到每种送风方案与正负理想解的联系向量距离和理想解的相对贴近度，如表7所示。其中，相对贴近度最接近1的方案，即为室内人员服装热阻为0.8 clo时的最佳送风方案。

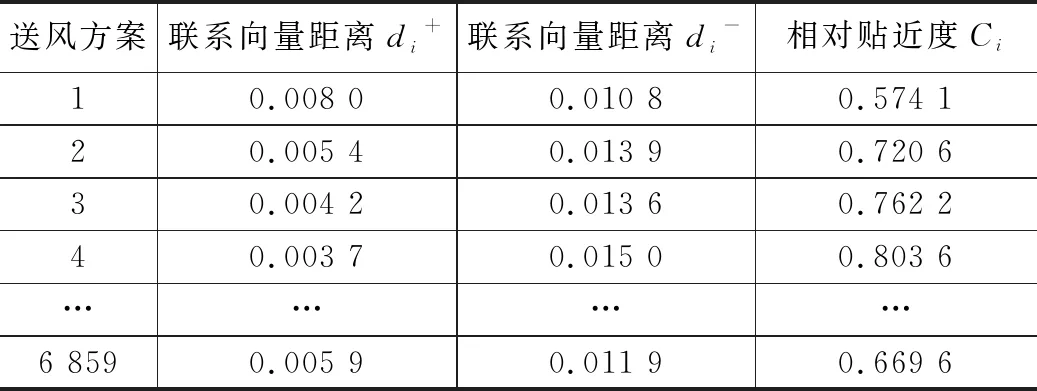
表7 联系向量距离和相对贴近度

本研究通过Design-Expert 12的Numerical Optimization模块和传统TOPSIS法也分别获得针对不同服装热阻的最佳送风参数，将3种方法所得到最佳送风参数进行比较，如图7所示。

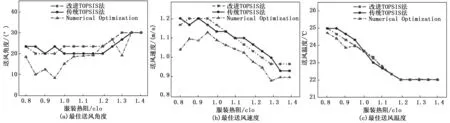
图7 不同服装热阻下的最佳送风参数

由图7可以看出：1)改进TOPSIS法与传统TOPSIS法优化的送风参数的大小和变化趋势基本一致;2)Numerical Optimization模块所获得的最佳送风温度与前两者相近，最佳送风角度和速度却差别较大;3)随着服装热阻的增大，最佳送风角度总体呈增大趋势，而最佳送风温度和速度呈下降趋势;4)当服装热阻大于1.3 clo时，最佳送风参数趋于稳定，基于改进TOPSIS法优化的最佳送风温度为22 ℃，最佳送风速度为0.97 m/s，最佳送风角度为30 °。

为了量化优化效果，本研究设置了一个基准方案作为优化前的送风方案，即在变量设计范围内取中间值，文献[11]证实了该量化方法的可行性。因此本研究中基准方案为：送风角度为30 °，送风速度为0.9 m/s，送风温度为25 ℃。为了衡量PMV的改善效果，本研究使用PPD代替PMV[11]。由图8可以看出，通风性能各项指标的优化效果显著，其中的舒适性指标PPD和垂直温差ΔT均达到ISO 7730的舒适性要求[14]。基于改进TOPSIS法与传统TOPSIS法优化后的通风性能最接近，而基于Numerical Optimization模块优化后的ΔT与前两者有较大差别，其值在部分供暖工况中出现大于优化前的ΔT，这是因为较大的EUC往往会导致室内出现较大的温度梯度。

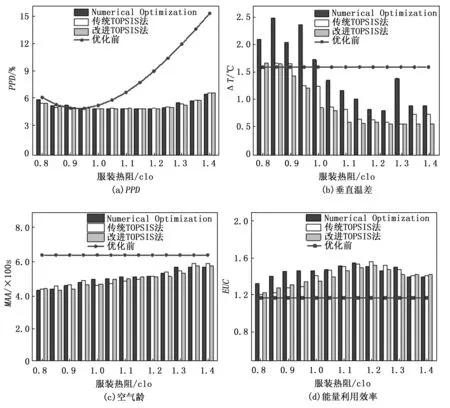
图8 优化前后的通风性能对比

表8为各项通风性能评价指标的平均优化效果。通过比较3种方法的平均优化效果可知，基于改进的TOPSIS法的优化效果最佳，PPD、ΔT和MAA分别平均降低了37.08%、48.17%和22.46%，EUC平均提高了20.42%。改进TOPSIS法的优化效果与传统TOPSIS法略有差别，这是因为在计算送风方案与理想解的联系度时考虑了对立集合的存在，在一定程度上克服了传统TOPSIS法的不足之处，从而使得计算结果更加可信。

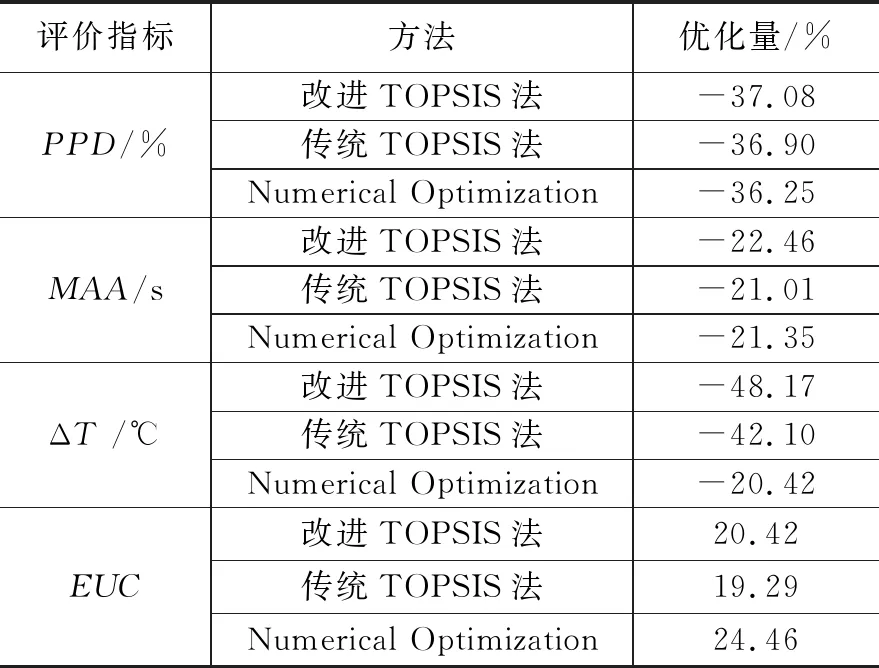
表8 通风性能评价指标的平均优化效果

4 结束语

为了满足室内人员在不同着装时对室内热环境的热舒适需求，同时改善空气质量、提高能量利用效率，本研究基于实验数据验证的CFD数值模拟，采用改进TOPSIS法对送风参数进行优化。详细结论如下：

1)各设计变量对通风性能各项指标的影响程度不一致，对PMV的影响程度从大到小为：服装热阻、送风温度、送风角度和送风速度；对ΔT的影响程度从大到小为：送风角度、送风温度、送风速度和服装热阻；对MAA的影响程度从大到小为：送风角度、送风速度、送风温度和服装热阻；对EUC的影响程度从大到小为：送风角度、送风温度、送风速度和服装热阻。

2)随着服装热阻的增大，最佳送风角度总体呈增大趋势，而最佳送风温度和速度呈下降趋势。此外，当服装热阻大于1.3 clo时，最佳送风温度为22 ℃，最佳送风速度为0.97 m/s，最佳送风角度为30 °。

3)基于改进TOPSIS法的送风参数优化显著地改善了层式通风供暖的通风性能，PPD、ΔT及MAA分别平均降低了37.08%、48.17%和22.46%，EUC平均提高了20.42%。其中的舒适性指标PPD和垂直温差ΔT均达到ISO 7730的舒适性要求。

4)建立通风性能评价指标与设计参数之间的函数关系可以在节约计算成本的同时，较为精准预测各送风方案的通风性能，还可以用于指导层式通风供暖工程设计。

5)基于改进TOPSIS法与传统TOPSIS法优化的送风参数的大小和变化趋势基本一致，说明了改进TOPSIS法具有可信性。