基于激光雷达的多关节机器人姿态自动控制研究
莫 毅,卿启新
(1.广西工业职业技术学院 电子信息学院,南宁 530001; 2.广西科技大学 自动化学院,广西 柳州 545006)
0 引言
激光雷达是一种特殊雷达系统,能够借助激光束探测目标对象所处位置,可以将速度、频率等特征量测量指标反馈回控制主机。与其他类型的雷达探测系统相比,激光雷达设备可以根据探测激光束与目标回波之间的差异性,获取与测量目标相关的参数信息。无论目标对象处于静态或动态运动态势,控制主机都能对其进行准确地跟踪与识别[1]。激光雷达探测系统由激光发射器、光学接收设备、信息处理平台等多个结构组成。激光发射器元件将输入电脉冲信号转换成光脉冲信号发射出去,光学接收设备再将所接收到的光脉冲信号还原成初始电脉冲信号,以便于显示器设备可以完整表现出探测对象的存在状态[2]。
多关节机器人也叫关节机器人或关节机械手臂,其各个连接关节的运动形态都是转动的,故而整体形态与人的手臂极为类似[3]。当某个关节出现转动时,其与核心连杆在空间方向上会产生一个相对移动量,若相对移动量的取值相同,则机器人关节的转动角度数值也相同,由于机器人运动姿态会随着转动角数值的变化而发生改变,所以一台多关节机器人需要由多台计算机设备进行控制。为了保持机器人运动行为的稳定性利用模型降阶与链式结构的机械臂位姿控制算法将整个控制过程划分为多个阶段,根据被动连杆姿态角的变化幅度确定中间姿态角的当前转动数值,再联合目标姿态角偏转程度的求解结果,判断多关节机器人是否出现明显的运动晃动情况[4]。然而此方法并不能有效控制机器人坡面行进步长与平坦地形直行运动步长之间的差值水平,在维持机器人运动稳定性方面的能力不足以满足实际应用需求。
为解决上述问题,设计基于激光雷达的多关节机器人姿态自动控制方法。
1 激光雷达定位导航技术
利用激光雷达实现多关节机器人姿态的定位与导航涉及如下两方面问题:1)如何掌握机器人在雷达地图中的具体位置;2)根据激光脉冲光束的传输情况,制定合理的运动路线。激光雷达定位导航技术要求在指定运动空间内设置多个目标位置节点,在每个节点上装配反射板结构[5]。机器人在移动时,激光雷达设备对反射板进行集中扫描,导航主机自主选择并记录三个以上反射板所处位置,再通过几何计算的方法对相关运动参数进行解析,通常情况下的定位导航遵循“三角法”原则,具体参考图1。
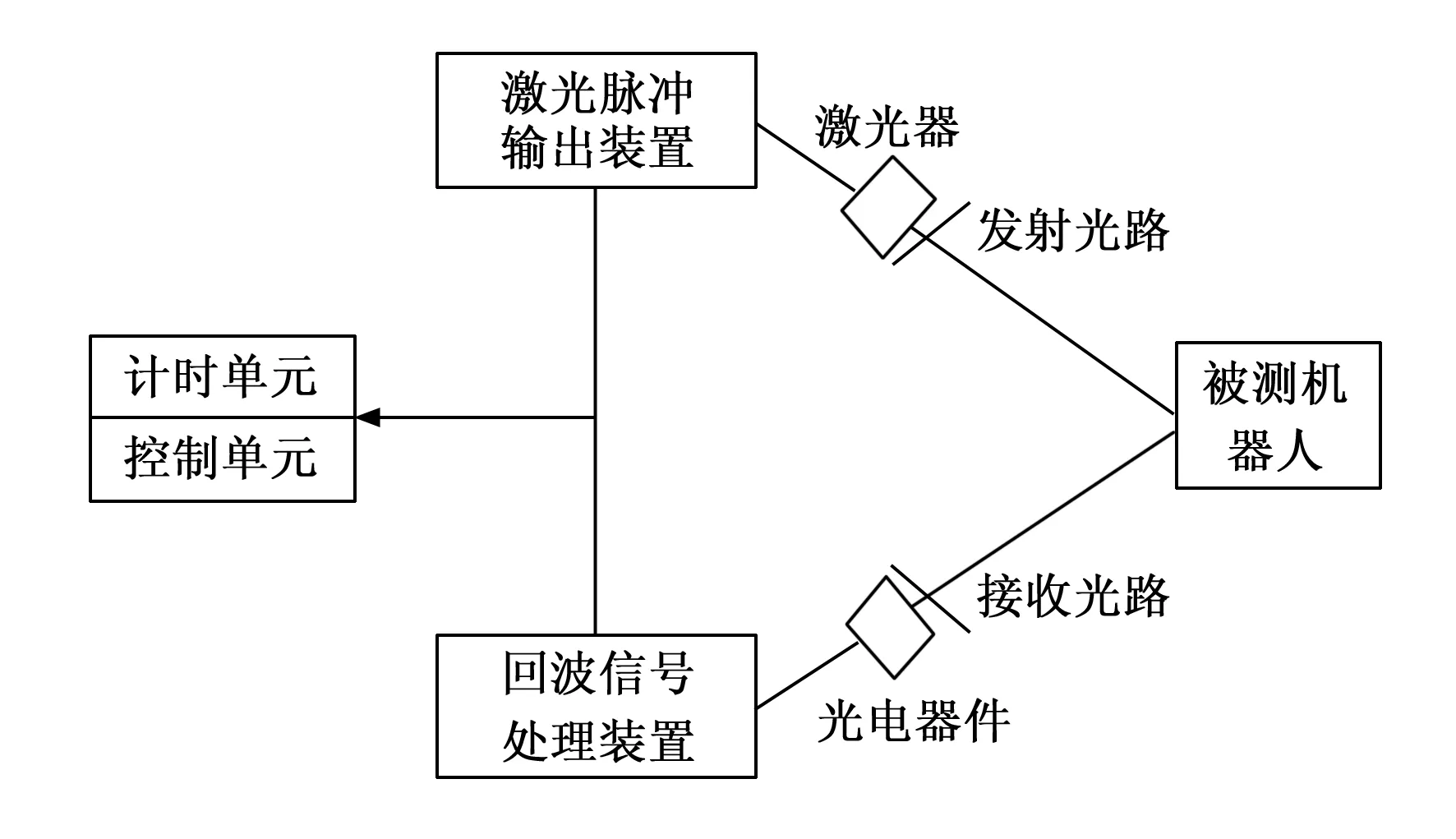
图1 激光雷达定位导航原理
激光脉冲输出装置借助激光器元件将光波信号发射至被测机器人所处位置,而回波信号处理装置则借助光电器件对电量信号进行聚合处理,当回收信号强度达到既定数值标准之后,计时单元、控制单元开始统计激光雷达传输回路中的信号输出与回收总量,直至导航主机能够准确定位被测机器人的位姿形态[6-7]。
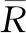
(1)
由于电脉冲输出信号不可能被完全转换成光脉冲回波信号,所以激光雷达传输回路中,光波信号的利用效率不会等于100%。
2 多关节机器人运动姿态
在激光雷达定位导航技术的支持下,完善CPG单元振荡器模型,再通过优化足结构参数的处理方式,生成完整的机器人行进路线,以此开展机器人运动姿态。
2.1 CPG单元振荡器模型
CPG单元振荡器为多关节机器人提供了运动过程中的动力支持。在机器人行进过程中,关节设备的变化状态由弯曲、伸展两种形式组成,故而CPG单元振荡器模型的运行状态也由包含两个部分。
2.1.1 关节设备弯曲
当机器人关节设备呈现弯曲状态时,激光信号快速输入信号集成设备之中,此时电量信号由振荡器回路“+”级传输至“-”级,振荡设备中生成大量的雷达射线,且这些射频信号的传输方向始终与电量信号的传输方向保持一致[8]。
2.1.2 关节设备伸展
当机器人关节设备呈现伸展状态时,已存储激光信号由集成设备继续向外传输,此时电量信号传输方向虽然由振荡器回路“+”级指向“-”级。由于所有传输信号的波动能力都相对较弱,故而振荡设备中的雷达射线不能继续向外传输,只能借助振荡器模型底层的CPG单元回路反馈给机器人足结构,从而使得机器人的运动步频与步长得到有效控制[9]。
完整的CPG单元振荡器模型连接回路如图2所示。
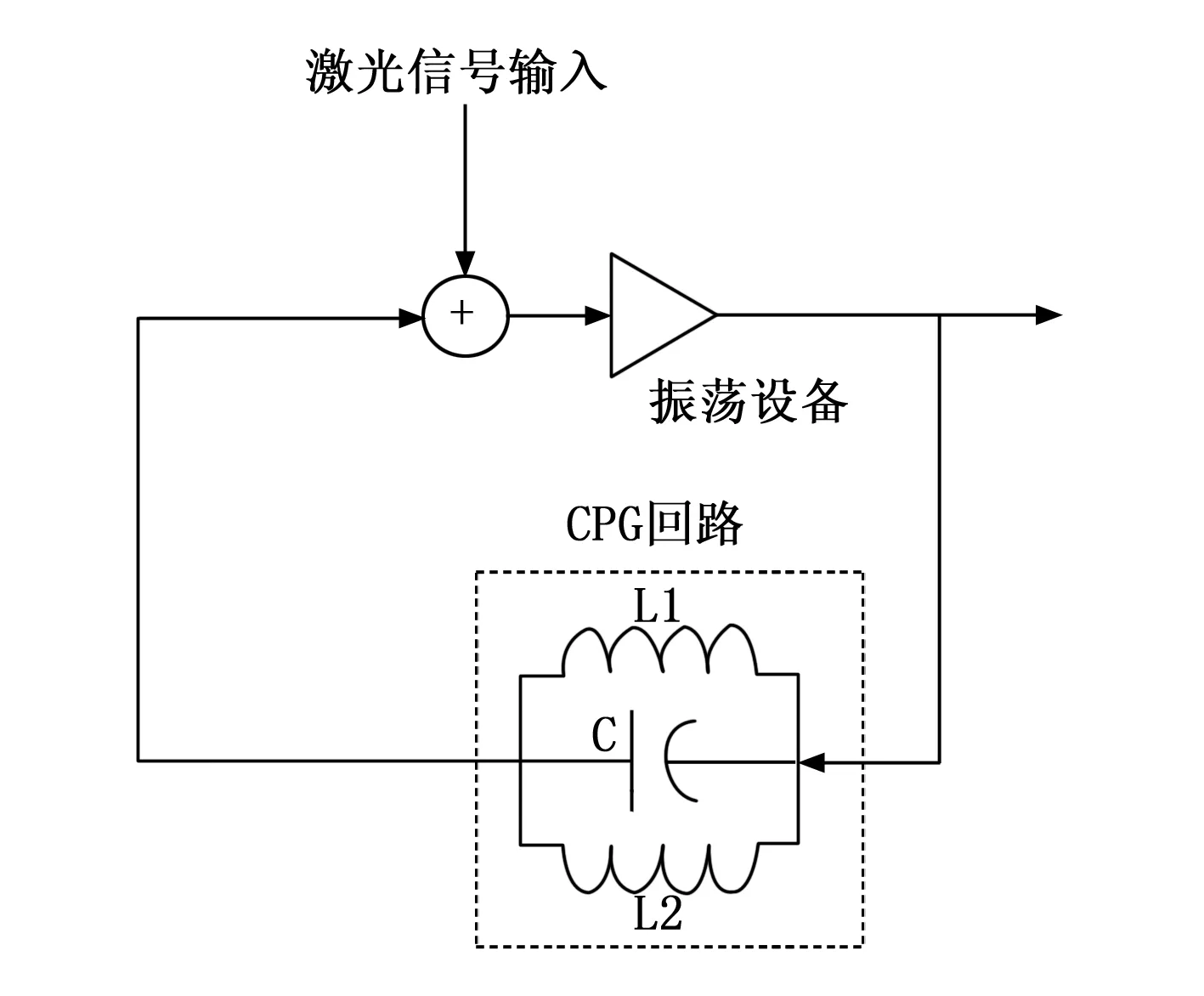
图2 CPG单元振荡器传输回路
CPG单元振荡器模型表达式为:
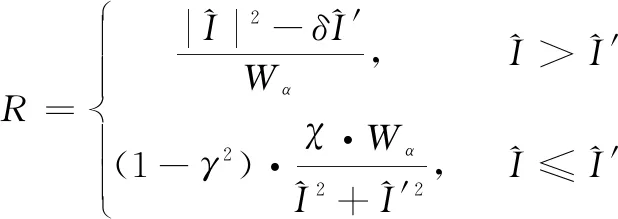
(2)
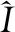
2.2 足结构参数优化
多关节机器人的工作环境较为复杂,故而利用激光雷达设备实现对机器人运动姿态的自动控制,此时要求机器人足结构具有较好的地形适应性与运动稳定性[10]。由于CPG单元振荡器结构是一个串并联并存的混合应用设备,所以当机器人足结构处于自由度较多的复杂运动环境中时,要求关节设备必须满足最基本的足结构运动性能。在CPG单元振荡器模型的支持下,以多关节机器人足结构作为研究对象,并对足结构尺寸参数进行优化处理,从而使得控制主机能够精准捕获处于同一运动平面内的机器人运动姿态节点[11]。设r1,r2,…,rn表示n个处于同一运动平面内的机器人关节姿态节点,γ1,γ2,…,γn分别表示与r1,r2,…,rn匹配的运动转向系数,U表示复杂度标记特征,联立上述物理量,可将多关节机器人足结构运动参数求解表达式为:
(3)
联立式(2)、式(3),可将足结构参数优化结果表示为:
(4)
其中:umax表示激光波振荡系数的最大取值,umin表示激光振荡系数的最小取值,ΔT表示单位运动周期。为避免复杂数据处理环节的出现,在划分单位运动周期时,要求机器人足结构运动形态应保持一致。
2.3 运动步态生成
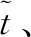
(5)
式中,ι表示目标姿态节点标记系数,iι表示目标位置处的机器人关节点坐标,i0表示机器人关节点的初始坐标,λ表示独立步态周期内的机器人运动强度。在激光器、光电元件所处位置保持不变的情况下,激光雷达信号传输路径也不会发生改变,这也是机器人运动步态路线内不会出现反向排布的姿态节点的主要原因。
3 机器人姿态自动控制实现
根据已生成的机器人运动步态行进路线,设定姿态参数指标,通过转换运动坐标的方式,求解动力学方程表达式,从而完善反馈控制器连接形式,实现基于激光雷达的多关节机器人姿态自动控制。
3.1 姿态参数设定
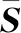
(6)
在式(6)的基础上,假设gx表示机器人运动姿态在X轴方向上的数值分量,gy表示Y轴方向上的数值分量,gz表示Z轴方向上的数值分量,且gx≠0、gy≠0、gz≠0的不等式条件同时成立,μ表示关节角标记系数。
多关节机器人的姿态参数设定表达式为:
(7)
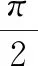
3.2 运动坐标转换
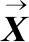
(8)
当待处理姿态节点不处于同一运动平面内时,需要根据平面转向角取值,建立两个关联平面之间的映射关系,将原节点在另一运动平面内的对应映射节点标记出来。按照姿态参数设定原则,判断当前节点之间的映射关系是否能够满足激光雷达光波的稳定传输需求。在此基础上进行运动坐标转换处理,直至所得结果能够清晰反映出机器人关节姿态节点的排列形式[17]。
3.3 动力学方程
机器人关节姿态动力学方程构建包括简化与分解、非线性耦合项参数化处理两个部分,本章节研究将针对上述内容展开。
3.3.1 简化与分解
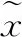
(9)
由于激光雷达光波在X轴、Y轴、Z轴方向上的投影长度不一定完全相同,所以当定义姿态坐标侧重方向不同时,所得动力学方程的简化与分解处理结果也会有所不同。
3.3.2 非线性耦合项参数化
非线性耦合项参数化注重对机器人运动姿态的方向转角进行度量,可以在动力学方程简化与分解表达式的基础上,限定位姿角的偏转情况,从而使得处理主机能够对偏转角参量进行更为细致的划分,也可有效抑制激光雷达光波变化[20-21]。设θx表示机器人运动方向角的X轴转向分量,θy表示Y轴转向分量,θz标准Z轴转向分量,ΔL表示机器人关节姿态的单位位移量,联立上述物理量,可将动力学方程非线性耦合项参数化处理结果表示为:
(10)
其中:ϖx表示X轴方向上的运动步长值,ϖy表示Y轴方向上的运动步长值,ϖz表示Z轴方向上的运动步长值。在机器人运动过程中,若关节姿态节点不存在跨越激光雷达光波传输平面的动力学行为,则非线性耦合项参数化处理结果不会出现变化。
3.4 反馈控制器
反馈控制器是一个完整的信号闭环结构,可以根据动力学方程表达式,标记机器人关节所处实时运动位置,将已记录节点与激光雷达光波的入射节点进行对比,以确定步长值向量的实际取值结果[22-23]。由于动力学方程非线性耦合项参数化结果并不能直接影响激光雷达光波的传输行为,所以建立反馈控制器闭环时,默认激光雷达光波的传输方向只在X轴、Y轴、Z轴方向上存在波长分量。设m1,m2,…,mn表示n个不相等的运动步幅向量,v表示关节角运动速度,b表示位姿角定义系数,ζ表示关节角偏转向量,σ表示位姿角偏转向量,联立式(10),可将基于激光雷达的多关节机器人姿态反馈控制器闭环表达式定义为:
(11)
多关节机器人姿态反馈控制器闭环设计过程中,除了要考虑激光雷达输出光波的定位能力外,还要确保反馈控制器结构呈现出完整的闭环连接状态,以此实现对于多关节机器人姿态自动控制。
4 实验结果与分析
4.1 实验准备
选择R6-0205型号的多关节机器人作为实验对象,如图3所示。

图3 多关节机器人实验设备
将其置于5.0~34.0 V的电压环境中,调节陀螺仪测量设备,使得MTi-G-700姿态传感器对于机器人关节角节点的控制精度保持为1。
表1记录了相关技术指标的实际取值范围。
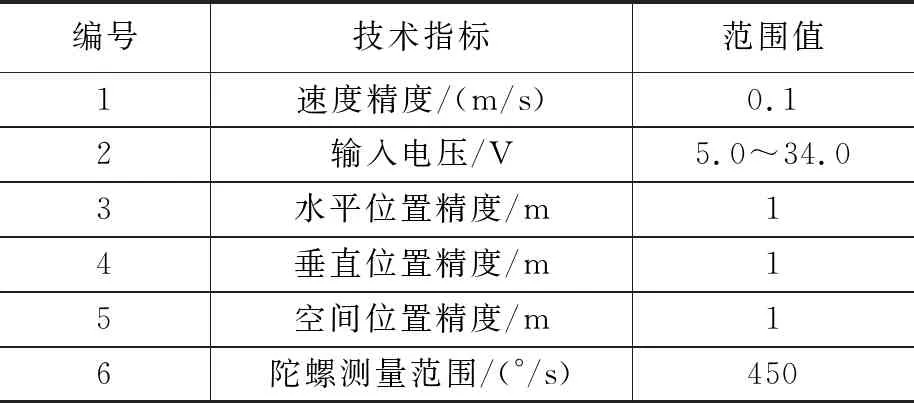
表1 技术参数表
实验组为基于激光雷达的多关节机器人姿态自动控制算法方法,对照组为基于模型降阶与链式结构的机械臂位姿控制方法,分别利用上述方法监测多关节机器人的坡面行进姿态,再将所得步长值数据与机器人平坦直行步长进行对比。机器人运动行为的激光雷达图像如图4所示。
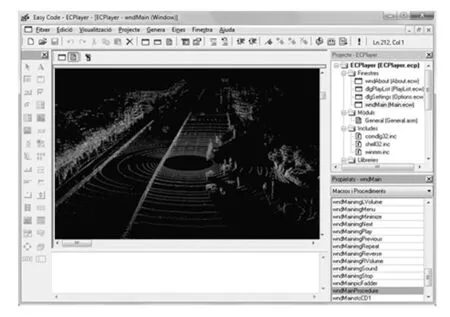
图4 机器人运动行为的激光雷达图像
监测机器人坡面行进姿态时,为避免关节角出现过度偏转的情况,应控制机器人运动速率保持较为稳定的数值状态。
4.2 数据处理与结果分析
机器人坡面步长与平坦直行步长之间的差值可以用来描述机器人运动行为的稳定性。一般来说,步长差值越小,就表示机器人的运动行为越稳定。对于多关节机器人设备来说,当其关节偏转角达到90°时,整个机械臂呈现水平状态,此情况下激光雷达的传输光波容易被主臂体结构遮挡,故而本次实验过程中,只记录关节角处于15~75°时,机器人坡面步长的数值变化情况。
图5反映了机器人上、下坡步长与平坦直行步长的数值对比情况。
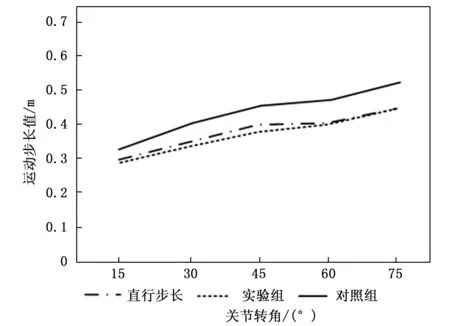
图5 机器人上坡步长
分析图5可知,随着关节转角数值的增大,机器人平坦直行步长呈现出不断增大的数值变化状态。当关节转角等于75°时,实验组上坡步长与当前情况下的平坦直行步长完全相等,二者之差为0;当关节转角等于45°时,实验组上坡步长与当前情况下的平坦直行步长差值最大,达到了0.02 m,即实验组上坡步长与平坦直行步长之间的数值最大误差为5%。当关节转角等于75°时,对照组上坡步长与当前情况下的平坦直行步长差值最大,达到了0.07 m,即对照组上坡步长与平坦直行步长之间的数值最大误差为15.6%,高于实验组误差水平。
分析图6可知,当关节转角等于15°、30°、45°、75°时,实验组下坡步长与当前情况下的平坦直行步长完全相等,二者之差为0;当关节转角等于60°时,实验组下坡步长与当前情况下的平坦直行步长差值最大,达到了0.03 m,即实验组下坡步长与平坦直行步长之间的数值最大误差为7.3%。当关节转角等于60°时,对照组下坡步长与当前情况下的平坦直行步长差值最大,达到了0.26 m,即对照组下坡步长与平坦直行步长之间的数值最大误差为61.9%,远高于实验组误差水平。
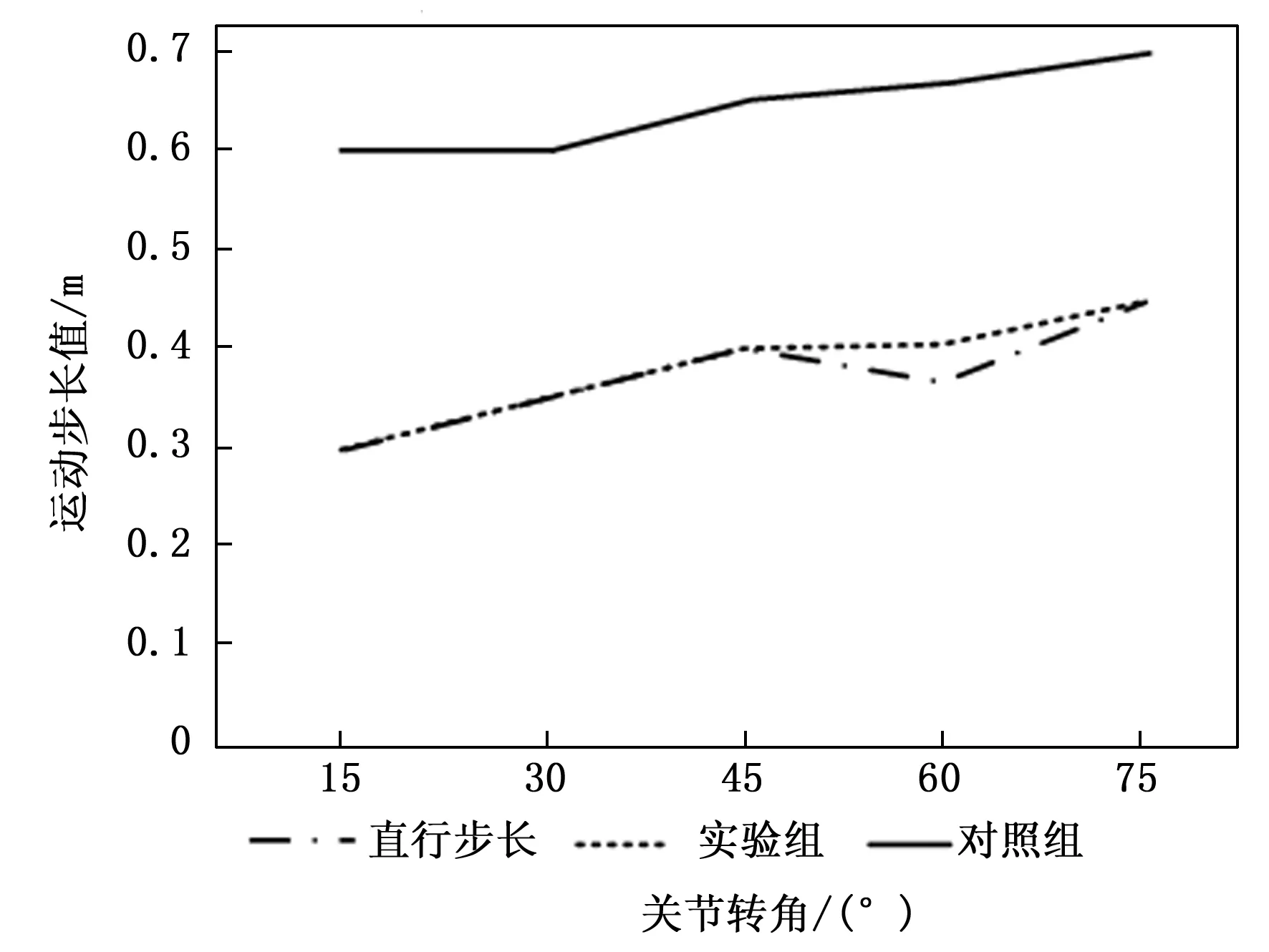
图6 机器人下坡步长
整个实验过程中,实验组机器人步长的数值状态明显更加稳定,这就表示在该控制算法作用下,机器人不会出现明显的晃动情况。
综上可知,本次实验结论如下:
1)基于模型降阶与链式结构的机械臂位姿控制方法在坡面运动状态下,不能有效控制实际步长与平坦直行步长之间的差值,不满足维持机器人稳定运动行为的实际应用需求;
2)基于激光雷达的多关节机器人姿态自动控制方法能够较好控制上、下坡步长与平坦直行步长之间的差值水平,对于维持机器人稳定运动行为能够起到明显的促进作用。
5 结束语
本文在激光雷达定位导航技术的基础上,建立CPG单元振荡器模型,又根据运动步态路线表达式,求解动力学方程,再按照运动坐标转换原则,调节反馈控制器闭环的连接状态。与基于模型降阶与链式结构的机械臂位姿控制方法相比,本文所设计的方法能够避免机器人坡面行进姿态与平坦地形直行姿态出现较大偏差,更符合维持机器人稳定运动行为的实际应用需求。此外,这种新型控制算法还能够准确辨别出机器人的上坡与下坡运动行为,并对其进行分别控制,这也是机器人在整个运动过程中不出现明显晃动行为的原因。

