琴键堰泄流能力数值模拟研究

王翔宇，池丽敏，刘学德，邵雨辰

（南京市水利规划设计院股份有限公司，江苏 南京 210001）

0 引言

很多专家学者对琴键堰进行了专门研究。中国水科院的耿云生与孙双科对琴键堰进行了模拟试验，郭新蕾等得出一个琴键堰的流量系数公式。随后李国栋等对琴键堰其他的条件进行了研究，指出了琴键堰可优化的方向。李珊珊等使用了全三维紊流数值模拟方法，对琴键堰的各个流量断面的泄流量进行了分析。姜铎等用三种上下游倒悬比不同的琴键堰进行了过流试验。于此，在前人研究基础上开展对琴键堰泄流能力数值模拟研究。先确定影响琴键堰泄流能力的一些参数，再通过FLOW-3D来模拟不同的来流流态、堰顶水头、泄流系数、消能率等参数对琴键堰泄流的影响规律。经过琴键堰泄流能力的数值模拟研究，可以更为深入地了解琴键堰泄流能力，探索改善琴键堰泄流能力的有效措施，为实际工程提供依据。

1 FLOW-3D软件的基本原理和基本方程

1.1 基本控制方程

FLOW-3D 软件求解流体运动方程采用先进数值计算技术，导入制作好的模型和初始调节输入即可模拟流体流动。

1.1.1 连续方程式

1.1.2 动量方程

将流体流速（u，v，w）在x，y，z三个方向的运动方程添加到N-S方程上：

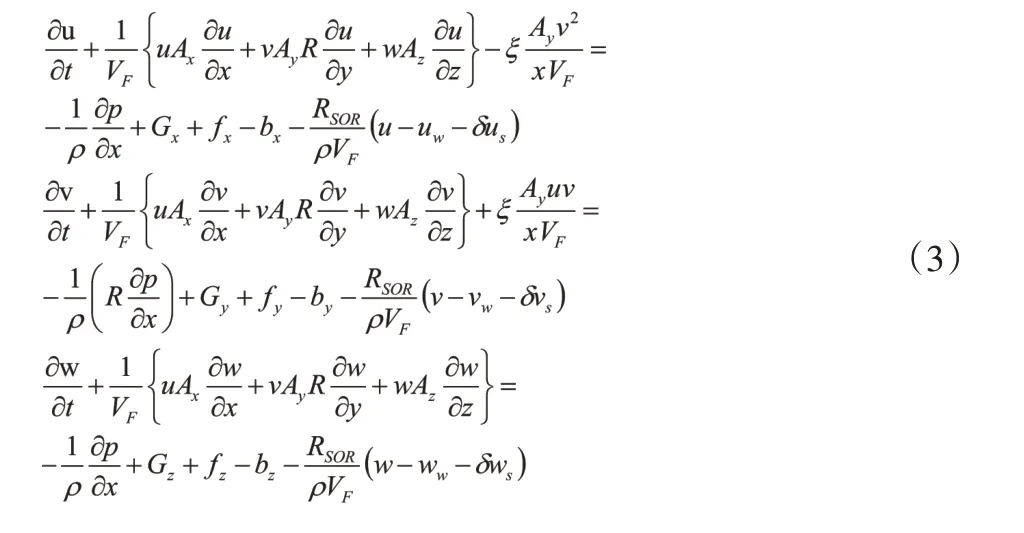
其中：Gx，Gy，Gz—为流体的加速度在x，y，z三个方向上的数值；bx，by，bz—经过导板或多孔介质的流体损失；fx，fy，fz—粘性加速度。

2 流场数值计算基本方法

流场数值解法一般分为耦合解法和分离解法两种。压力求解法是分离解法的一种，其本质就是迭代。每次计算时都要给出一个初始压力值，然后推断出速度初始值，最后再进行修正。之后循环这样的计算，就可以得出其收敛解。

FLOW-3D网格使用最简单矩形单元划分，易于生成网格，且需要空间较少，但数值精度较高。

边界条件是限制水流或是计算区域的条件。只有边界条件设置合理，符合模型适应的条件，才能计算正确流场解。进口边界条件所有的变量都是已经知晓的固定值。一般来说，进口断面一般取速度或者水深作为进口边界条件。上述的进口边界条件为第一类边界条件，而出口边界条件则是第二类边界条件。模型下游为自由出流，压力设置为0。壁面边界条件一般为所需研究的模型中的底板、边墙等。如果想要求得壁面边的流速，在壁边生成一个面，就可以在这个面上得到流速。一般在所有存在空气的边界处都定义为大气压强。

3 琴键堰泄流能力数值模拟研究

3.1 几何模型的建立

利用FLOW-3D 制作几何模型。首先用AutoCAD 画出三维模型，再保存为stl.格式。然后利用FLOW-3D 软件来模拟流体。所用的模型是借鉴文献中已有的模型来计算的，如图1所示。试验中将采用三种不同进出口宫室宽度WO、Wi的琴键堰模型各三种水深来验证。

图1 琴键堰模型示意图

基础模型数值数据见表1。

表1 琴键堰模型各种参数表

三种进出口宫室宽度WO、Wi不同的模型数据见表2。

表2 三种不同琴键堰模型的进出口宫室宽度表

3.2 网格的划分

鉴于Flow-3D建模能力不是很强，需要在AutoCAD中建立需要模型，然后将stl格式图档导入到Flow-3D中，再进行网格划分。Flow-3D的优点是在划分网格时可以使用矩形网格块，把要模拟的模型包裹在矩形块中。基本模型网格划分大约为694 000 个，第二模型网格划分大约为666 000 个，第三模型网格划分为666 000个，网格划分见图2。

图2 网格划分图

3.3 边界条件及算法

入口边界条件以水深为基础条件，上游为指定的水深水体，下游为自由出流，左右和底边都为墙，上面为与空气接触的自由水面。算法是有限体积法来隐式求解；速度压力的耦合采用GMRES法。

3.4 计算结果分析

模拟中进口宫室宽度Wi分别为2.40、3、2.10 cm，出口宫室宽度WO分别为2.40、2、2.60 cm 三种宽度计算和这三种模型深度为11、11.50、12 m来计算，从流态、堰上水头、泄流系数、效能率方面分析此次数值模拟计算结果。Flow-3D 可以自动将计算结果转换成图像，能更加直观地反应水流流动。

3.4.1 水流流态分析

以进口水深11 m，进出口宫室宽度2.40 m 为例分析水流流态。初始时整个琴键堰内没有过水，图3为水流在开始30 s内的整个流动过程及每隔3 s时的流速矢量图。

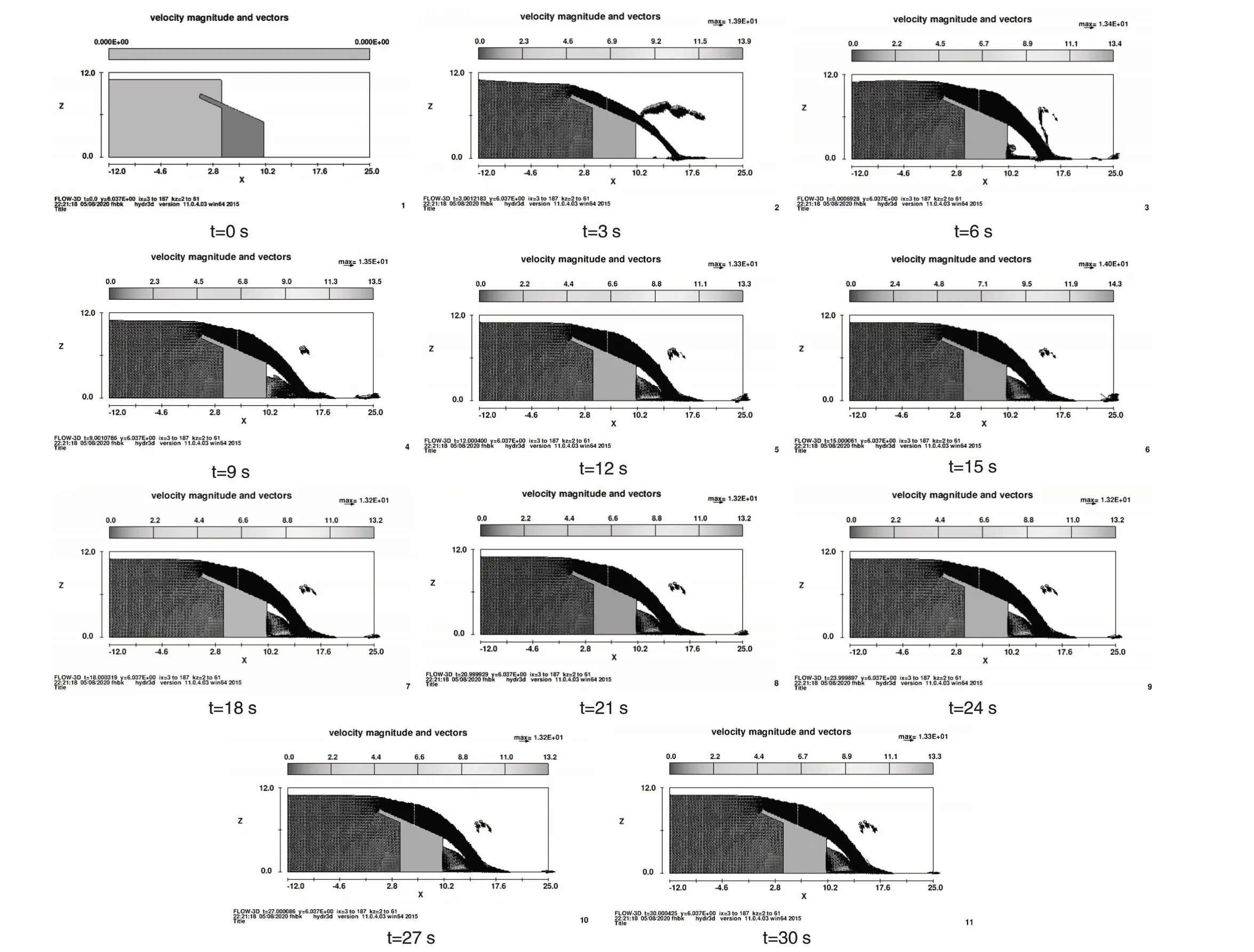
图3 水流30 s内的整个流动过程及每隔3 s时的流态图

琴键堰在过水时，水流呈现三元流，进口宫室的水流在开始时比较平稳，但是在通过琴键堰后水流急剧变化，使水流自由跌落至下游处。而出口宫室的水流为急流，来自上游处过堰水流和来自出口宫室两侧的进口宫室流入的水流，以射流的方式进入下游处，是为淹没水流。

3.4.2 堰顶水头分析

列表计算水深11 m三种不同进出口宫室宽度模型的堰顶水头。见表3。

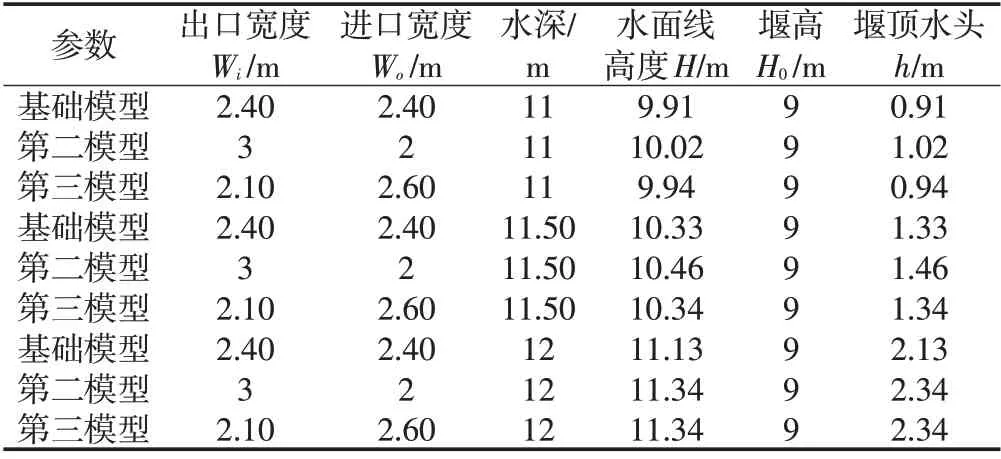
表3 不同进出口宫室宽度在三种水深下的琴键堰堰顶水头表

当Wi=Wo=2.40 m 时，得出x=1.09 时，求得水面线高度H1为9.91 m，此时堰高为9 m，所以堰上水头为9.91-9=0.91 m。

当Wi=3 m，Wo=2 m时，得出x=1.10时，求得水面线高度H1为10.02 m，此时堰高为9 m，所以堰上水头为10.02-9=1.02 m。

当Wi=2.10 m，Wo=2.60 m 时，得出x=1.10 时，求得水面线高度H19.94 m，堰高9 m，所以堰上水头为9.94-9=0.94 m。

表3 可知，进出口宫室宽度2.40 m 时堰顶水头最小，琴键堰泄流量合理。

3.4.3 泄流系数分析

分析三种不同的进出口宫室宽度琴键堰模型在水深为11、11.50、12 m时的泄流系数见表4。琴键堰的流量系数与m，H，B，Q有关。

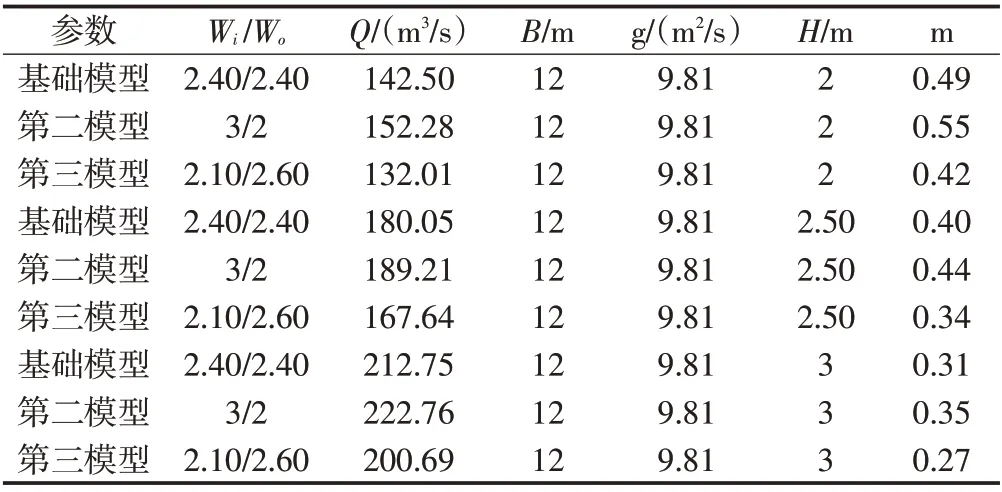
表4 不同进出口宫室宽度在不同水深下的流量系数表

来计算其流量系数。B，g为固定值，H有三种情况，m，Q有九种情况。

由表4得出，当琴键堰的总宽度B一定时，琴键堰的尺寸也不变时，随着堰上水头的增加，它的流量也随之增加，得到其流量系数减小；反之，当琴键堰的总宽度B一定时，琴键堰的尺寸也不变时，随着堰上水头的减小，它的流量也随之减小，得到其流量系数增大。当其总宽度B和堰上水头H一定时，随着进口宽度变大，出口宽度变小，则它的流量就增大，其流量系数就增大。

3.4.4 消能率分析

利用上游和下游能量守恒定律来计算琴键堰消能率。使用FLOW-3D 的时候得出其流速。然后根据得出的流速来计算琴键堰上游截取断面和下游截取断面的总能量。消能率的计算方法是用两能量之差比上游截取断面的能量即：

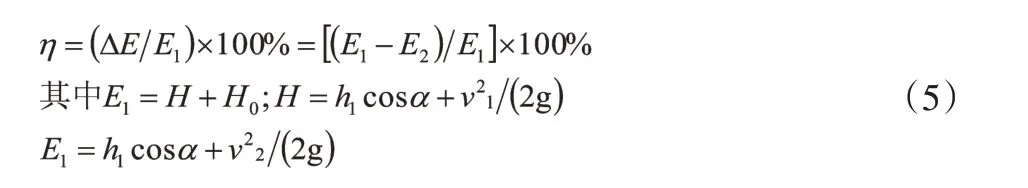
式中：ΔE为琴键堰上游所取断面和下游稳定后断面的能量差；E1是上游所取断面的总能量，E2为下游稳定后所取断面的总能量；H为琴键堰开始断面的水深势能和动能之和；H0为开始断面和结束断面的高差；h1为上游所取断面的水深，h2为下游稳定后断面的水深；α为宫室底边的倾角；v1为上游所取断面的流速，v2为下游稳定后断面的流速；g为重力加速度。

三种进出口宫室宽度不同琴键堰消能率见表5。

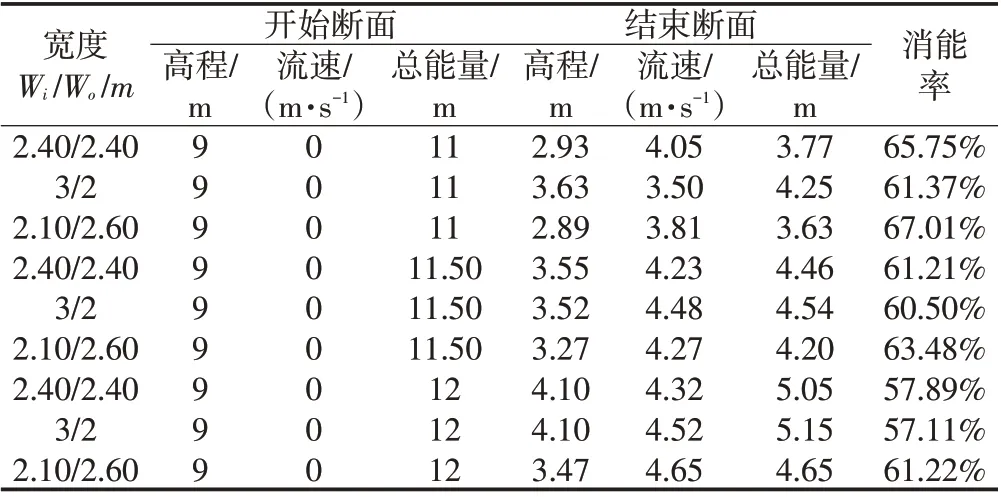
表5 三种不同进出口宫室宽度的琴键堰消能率表

4 结语

①琴键堰过水时，水流呈现三元流，进口宫室水流开始时比较平稳，通过琴键堰后水流急剧变化，使水流自由跌落至下游处。而出口宫室的水流为急流，来自上游处过堰水流和来自出口宫室两侧的进口宫室流入的水流，以射流方式进入下游处，是为淹没水流。②当进出口宫室宽度都为2.40 m时，则堰顶水头最小，其泄流量合理，此时最适合泄流。③当琴键堰的总宽度B一定时，琴键堰的尺寸也不变时，随着堰上水头的增加，它的流量也随之增加，得到其流量系数减小；反之，当琴键堰的总宽度B一定时，琴键堰的尺寸也不变时，随着堰上水头的减小，它的流量也随之减小，得到其流量系数增大。当其总宽度B和堰上水头H一定时，随着进口宽度变大，出口宽度变小，则它的流量就增大，其流量系数就增大。④当堰上水头一定时，进口宫室宽度变小时，它的消能率随之增加；当琴键堰尺寸不变时，其堰上水头越高，则消能率越低。