基于枚举法和遗传算法的农田有压管道系统优化设计

曹风华

（温陈街道农林水综合服务中心，山东 聊城 252131）

1 引言

近年来，许多专家学者针对供水成本展开研究。陕永杰等人基于数学模型，对某地区供水系统进行优化，以控制其用水量和成本。高淑会等人利用成本分摊方法，对某调水过程的供水成本进行计算，分析出水量的变化规律。姬鹏程等人对某工程的供水成本进行分析，并根据其工程实际情况，提出相关建议，以控制供水成本。马婧等人基于LCC方法，分析供水管网的全生命周期成本，结合实际工程案例，确定其最优方案。谢永刚等人以某地区湿地为研究对象，针对其实际情况，提出相关供水成本优化方案。选取某地区农田有压管道，基于枚举法和遗传算法，对比分析不同管网布置方案下的供水成本，选取最优灌溉方案。

2 有压管道模型的建立

2.1 目标函数

以某地区农田有压管道为研究对象，建立其优化模型，以优化其灌溉成本。为达到最低灌溉成本，以此为目标函数，建立优化模型。灌溉成本主要包括固定资产折旧费和运行成本，二者之和除以灌溉水量即为灌溉成本。

2.1.1 固定资产折旧费

灌溉过程中主要使用的设备为泵站和管网，折旧费主要根据泵站工程的建设费用（W1）和管网工程的建设费用（W2）计算，其计算公式如式（1）、式（2）：

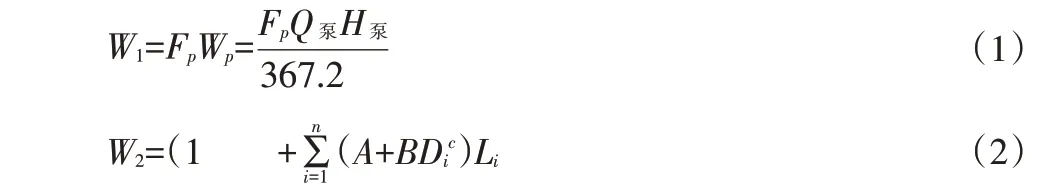
式中：Fp为泵站平均装机容量所需金额，元；Wp为泵站容量，kW；η装为装机效率，Q泵为设计流量，m3/s；H泵为设计扬程，m。θ为设施费占比，τ为人工费、机械费占比，Di为管道内径，mm；Li为管道长度，m；A、B、c为造价系数。

根据泵站工程建设费用和管网工程计算工程固定资产（W），计算公式如式（3）：

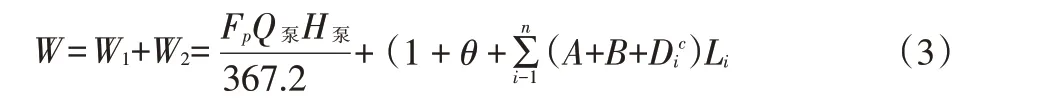
根据上述工程固定资产计算公式，计算固定资产折旧费（F）如式（4）：

式中：；T为灌水周期，d；t为每天灌水时间，h。

根据工程固定资产和折旧费计算公式，推导出灌溉成本计算公式，如式（9）所示：

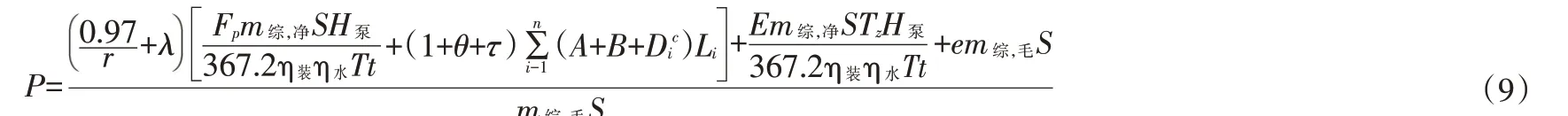
2.2 约束条件

2.2.1 管径约束

管径的约束应复合式（10）：

式中：Hk为工作水头，m；Hc为最大压力，MPa。

3 数学模型求解

3.1 管道布置优化

根据农田所在地区的相关情况，在农田布置给水栓。为优化管道布置，首先需要根据给水栓的位置，对管网整体进行优化。根据水流速度，方向和该地区的地理位置、地貌特征，选取灌溉的最短路径。

在管网连接图中，共有10个供水节点，根据该地区的实际情况和每个供水节点的需水情况，对10个供水节点进行编号，并且确定各供水节点之间的关系，如图1所示。由于供水管道路径的复杂性，其供水方案较多。例如，管段［1］、［3］、［4］、［12］、［13］、［21］、［24］、［26］、［28］可为一组供水方案。针对上述方案，采用枚举法进行分析，将供水方案的数据作为矩阵进行分析，由于计算量巨大，且计算过程繁杂，采用C++进行计算，以得出优化方案。

3.2 管径优化

3.2.1 编码

由于供水管道的内径尺寸具有冗余性，所以采用取整的方法对其进行编码。研究共有11 种供水管道，其管径分别为［200，180，225，90，125，160，140，110，110，90］，对其进行取整编码，则可得［8，7，9，2，4，6，5，3，3，2］。根据以上对供水管道的编码，采用遗传算法，对供水管道的内径尺寸进行分析。

3.2.2 遗传算子

以轮盘赌选择作为选择算子，采用两点交叉法，取其较差概率为0.70，其结果如下。

交叉前：［2丨528丨912］ ［2丨316丨912］

交叉后：［1丨316丨711］ ［1丨528丨711］

对交叉后的算子进行变异处理，取变异系数为0.10，变异后结果如下：

变异前：［2，3，1，6，9，12］ 变异后：［2，2，1，6，9，12］

4 工程案例

灌区位于山东省内，采用有压管道进行引水，根据灌区该地区的实际情况和每个供水节点的需水情况共设置9 个供水节点，对9 个供水节点进行编号，并且确定各供水节点之间的关系，如图1所示。管网各节点的数据如表1所示。农田灌溉系统的相关参数如表2所示。

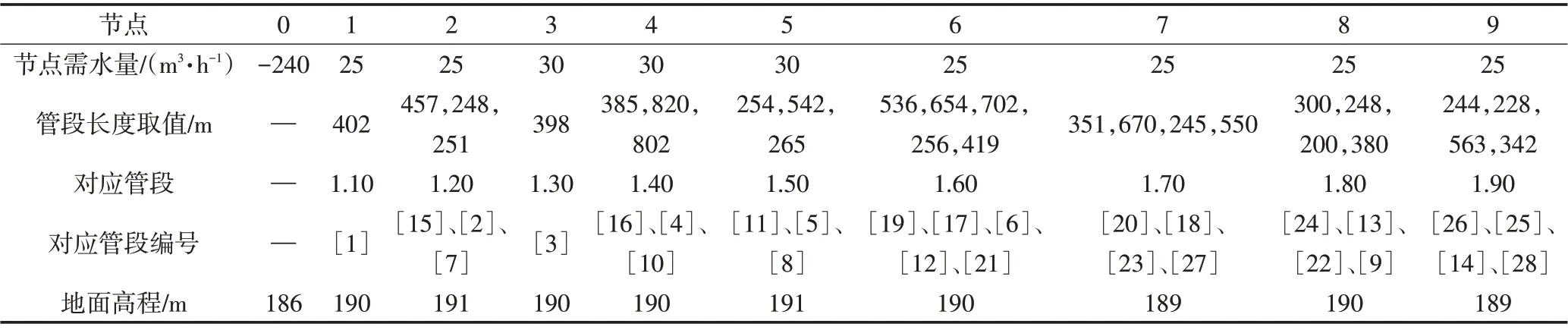
表1 管网各节点与管段数据表

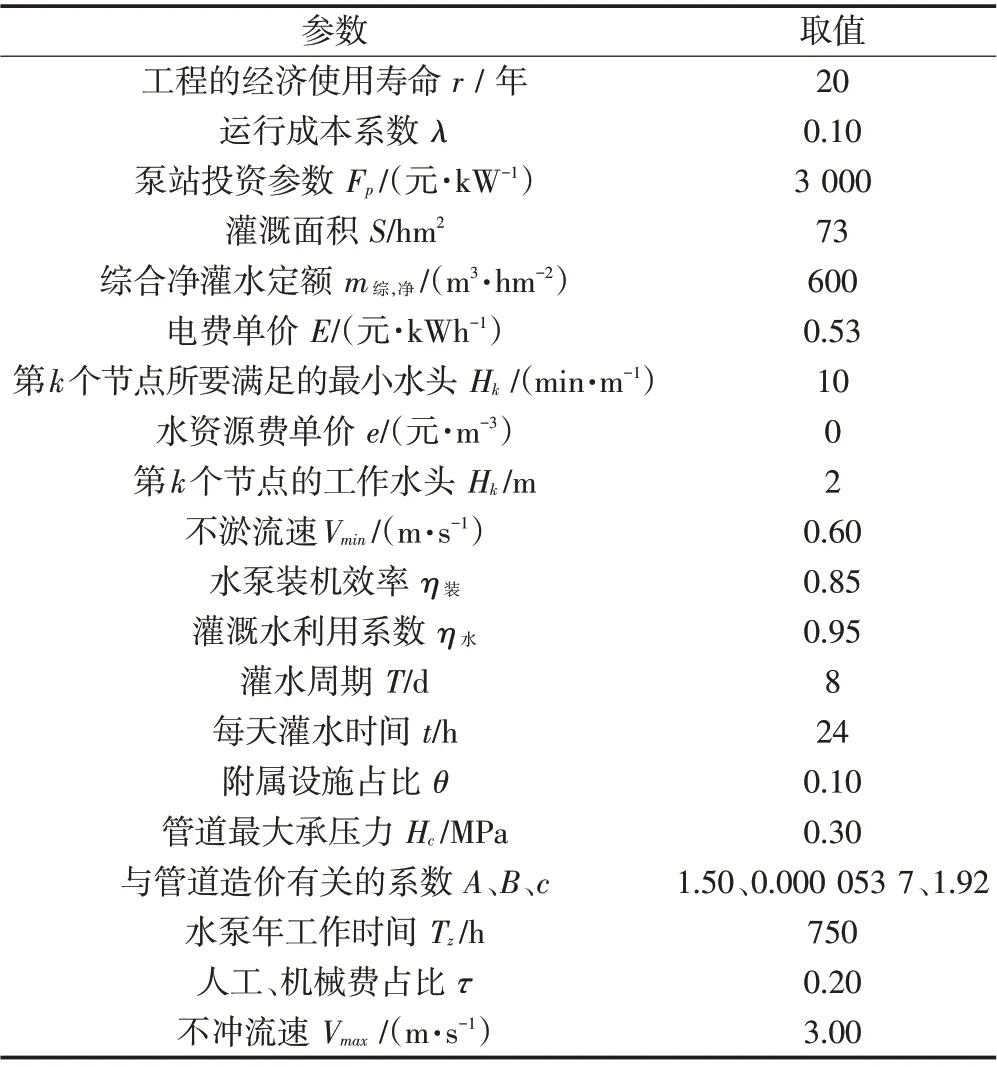
表2 农田灌溉系统相关参数表

5 结果分析

共有9个供水节点，根据该地区的实际情况和每个供水节点的需水情况，对9 个供水节点进行编号，并且确定各供水节点之间的关系，如图2所示。

图2 供水节点关系图

根据上述分析可得，取管网长度为2 865 m，所需灌水成本为每立方米0.49元。采用C++对管网进行优化设计分析，程序相关参数如表3所示。

表3 程序相关参数表

采用Matlab R2014 a对优化设计后的数据进行编程，编程相关参数如表4 所示。通过Matlab R2014 a 进行处理后，得到其最优管网布置形式如图3所示。

表4 Matlab R2014 a相关参数表

图3 最优管网布置形式图

为了有利于对比分析，图3 所示的供水方案有所重叠，所以在其中选取农田灌水成本最低的方案，不同管网优化方案如表5所示。

表5 管网优化方案表

由表可知，方案9的供水成本最小，为0.314 2 元/m3，方案6的供水成本最大，为0.515 3 元/m3，所以选取方案9时有最小灌溉成本，为最优管网方案。再此方案中，对应管段管径为75，200，90，75，75，180，75，110，75；所包含的管段为［1］、［2］、［3］、［16］、［11］、［12］、［23］、［24］、［25］；水泵扬程为20.40 m；管网总长度为2 721 m。

不同管网布置方案对应的供水成本如图4 所示。由图可知，供水成本与遗传代数呈负相关关系，随遗传代数的增大，供水成本逐渐减小。当遗传单数大于20 时，供水成本变化趋势趋于平稳，逐渐趋于一个定值。当管网总长度为2 620 m时，供水成本最大，当管网长度为2 721 m时，供水成本最小，此时为最优农田有压管道灌溉方案。

图4 供水成本变化曲线图

5 结论

以某地区农田有压管道为研究对象，根据该地区的实际情况和每个供水节点的需水情况，对9 个供水节点进行了编号，并且确定了各供水节点之间的关系和布置形式。同时基于枚举法和遗传算法，对比分析不同管网布置方案下的供水成本，对其进行优化，选取最优灌溉方案。结论如下：①方案9的供水成本最小，为0.314 2元/m3，方案6的供水成本最大，为0.515 3元/m3，所以选取方案9时有最小灌溉成本，为最优管网方案。再此方案中，对应管段管径为75，200，90，75，75，180，75，110，75；所包含的管段为［1］、［2］、［3］、［16］、［11］、［12］、［23］、［24］、［25］；水泵扬程为20.40 m；管网总长度为2 721 m。②供水成本与遗传代数呈负相关关系，随遗传代数的增大，供水成本逐渐减小。当遗传单数大于20时，供水成本变化趋势趋于平稳，逐渐趋于一个定值。当管网总长度为2 620 m时，供水成本最大，当管网长度为2 721 m时，供水成本最小，此时为最优农田有压管道灌溉方案。