基于混合模型的云平台资源弹性伸缩方法
贺敬伟,戚林成,杜元翰,张世杰,刘继东
(1.江苏电力信息技术有限公司,江苏 南京 210000;2.国网江苏省电力有限公司信息通信分公司,江苏南京 210000)
混合模型是集中不同应用模型的组合体表现形式,其允许所研究项目向着最有效的路径发展。除随机误差条件外,也可定义为固定效应、随机效应两类基本的统计分析原则。在统计学范畴中,混合模型代表了原始大群体中存在子群体的数学概率,一般来说,与混合模型匹配的数据集合空间越大,子群体被应用主机直接采纳的可能性也就越大[1-2]。若将统计推断条件考虑在内,则可认为随着子群体数量值水平的增大,混合模型的原始包含空间也会不断扩大,但由于随机误差量的存在,子空间对于原始空间的数值影响条件也会随之不断改变。
在云平台环境中,为了从根本上保障云服务的质量水平,应对资源数据存储条件进行及时适量的匹配。传统高斯负载型数据伸缩方法通过计算正向超量时延系数的方式,确定云平台资源数据的实时存储条件,再根据既定的残差值分析标准,实现对数据信息的拉伸与收缩处理。然而此方法的最小压缩与最大拉伸能力有限,并不能实现对云资源数据传输体积的及时调整。
为解决此问题,提出基于混合模型的云平台资源弹性伸缩方法,根据资源数据的初始定位条件,确定云平台主机需求的实际变化趋势,再通过资源数据采集与融合的处理方式,完善已定义的弹性扩容与伸缩扩容条件。
1 基于混合模型的云数据定位
基于混合模型的云数据定位由聚类混合系数计算、初始定位条件确定、云数据优选残差加权量分析三个处理环节共同组成,具体研究方法如下。
1.1 聚类混合系数
聚类是将已知云数据特征矢量全部划分至不同模型类别中,再将所得模型集合体按照一定标准混合,以便于后续协方差计算。协方差指标能够约束云平台资源在单位时间内的传输能力,一般情况下,混合模型的初始数值空间越大,已存储资源信息之间的协方差指标数值水平越高[3-4]。
设i0代表最小的云数据存储系数,in代表最大的云数据存储系数。其中,n表示聚类处理的实际执行次数。在由i0、in决定的云数据存储空间中,混合模型所涉及的云数据信息总量值越大,最终计算所得的聚类混合系数值也就越精准。联立上述物理量,可将聚类混合系数表达式定义为:

其中,w1代表第一个应用模型聚类条件,wn代表第n个应用模型聚类条件,代表待存储云平台资源数据特征值,代表聚类模型的混合特征均值。
1.2 初始定位条件
初始定位条件是混合模型建立的关键,可在已知聚类混合系数结果基础上,限定云平台资源数据所能达到的传输与存储位置[5]。由于混合模型存在相对复杂的数据信息存储限定条件,在考虑聚类作用的情况下,随着云平台资源数据传输速率的加快,相关信息参量的存储位置也会逐渐发生改变。为更好适应上述资源信息变化情况,应选取多个不同云平台数据作为聚类参考条件。一方面,借助混合模型对相关信息参量进行整合,另一方面也可较好控制模型主体在单位时间内的具体变化情况[6-7]。设m1、m2、…、mn分别代表n个不同云平台资源数据信息,λ表示混合模型的单位聚类条件,联立式(1),可将混合模型的初始定位条件表示为:

其中,u0代表最小的资源数据传输速率值,un代表最大的资源数据传输速率值,R代表标准的平台资源数据聚类系数项。
1.3 云数据的优选残差加权量
云数据的优选残差加权量从随机解角度出发,通过寻优迭代处理的方式,确定混合模型的最优解数值,再借助适应度函数,评价云平台资源的存储与应用价值,从而实现对混合模型执行环境的有效完善。在已知初始定位条件的前提下,通过聚类处理等方式所获得的优选残差加权量计算结果,能够从强弱度、分离度等多个角度分析云平台存储环境的稳定性水平[8-9]。云数据优选残差加权量作为一种正值误差特征量,在参量选取与计算过程中,只能将其视为一种估算值应用结果。
设表示云平台环境中资源数据信息的残差优选系数,代表与混合模型匹配的强弱度参量值,β代表与混合模型匹配的分离度参量值,联立式(2),可将云数据的优选残差加权量计算结果表示为:

其中,An代表云数据信息的残差量最大值,Aˉ代表云数据信息的残差量均值,ΔY代表单位时间内的云平台资源数据传输变化量。
2 云平台资源的弹性伸缩方法
在混合模型支持下,按照平台主机需求变化趋势分析、资源数据采集与融合、弹性扩容与伸缩扩容条件计算的处理流程,完成云平台资源弹性伸缩方法的设计与应用。
2.1 平台主机需求变化趋势
针对云平台所有特定资源数据的弹性伸缩变化策略,需要根据平台主机的需求制定条件,且由于混合模型的存在,数据信息参量在实际存储过程中,始终保持较强的感应性传输能力[10-11]。不同存储时刻,云平台资源数据具备的弹性伸缩适应能力也有所不同,在已知优选残差加权量计算结果的情况下,待存储的资源数据量越大,云平台主机所具备的信息传输能力也就越强。在单位传输时间内,云平台资源数据始终保持连续转存的物理变化形式,即随着平台运行时间的延长,资源数据的转存量水平也会不断增大,反之则不断减小[12]。
设θ1、θ2分别代表两个不同的云平台感应需求条件,在资源数据查找量等于β的情况下,联立式(3),可将云平台主机的需求变化趋势定义为:

其中,f代表云平台环境中的资源数据转存系数,代表单位时间内的云平台资源查找均值量,η代表资源数据的传输效率,k0代表数据信息的初始存储量数值。
2.2 资源数据的采集与融合
云平台资源数据采集与融合是信息参量处理的关键环节,其可在已知混合模型的基础上,安排弹性伸缩控制指令的执行强度,实现对弹性扩容与伸缩扩容条件的准确计算。从宏观角度来看,资源数据采集与资源数据融合是两个相互独立的执行流程,前者负责在云平台环境中分析资源数据所处的实时位置,并结合混合模型对主机中暂存的信息参量进行按需提取;后者则主要负责将散乱分布的资源数据整合成包状传输形式,从而实现对弹性收缩控制指令的有效分配与调节[13-14]。采集与融合流程如图1所示。

图1 云平台资源数据的采集与融合流程
2.3 弹性扩容与伸缩扩容条件
弹性扩容条件决定了云平台资源数据的最大存储能力,一般来说,资源数据的采集与融合情况越完整,弹性扩容条件的计算结果也就越精确[15]。设ξ表示既定的云平台资源数据采集系数,j表示单位时间内的资源数据融合处理系数,联立式(4),可将弹性扩容条件表示为:

其中,h代表单位时间内云平台资源数据的最大采集量。
伸缩扩容条件决定云平台资源数据的最小存储能力,该项物理条件与弹性扩容条件之间的差值水平越大,云平台空间的实际稳定性能力也就越强[16]。设d代表云平台资源数据的实时容量系数值,μ代表数据信息的弹性伸缩目标向量,联合上述所有已知条件,可将伸缩扩容条件表示为:
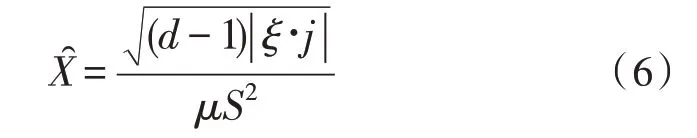
至此,完成各项物理系数值的计算与处理,实现云平台资源弹性伸缩方法的研究。
3 实例分析
在云平台环境中,最大拉伸值、最小压缩值都能反映主机设备所具备的资源数据处理能力。理想情况下,云平台资源最大拉伸值的理想变化区间为5~13 bit(如图2 所示),且数值结果越大,达标拉伸处理行为越明显,其理想情况如图2 所示。

图2 最大拉伸值的理想变化情况
将与理想拉伸值结果对应的时间节点作为时间取样点,绘制实验组、对照组最大拉伸数值的实际变化曲线。其中,实验组采用基于混合模型的云平台资源弹性伸缩方法,对照组采用高斯负载型数据伸缩方法[17-19]。
对比图2、图3 可知,实验组、对照组的最大拉伸值曲线始终与理想曲线保持相同的变化趋势,但实验组均值水平明显更高,变化区间范围由5~13 bit 扩大为8~16 bit;对照组均值水平则显著降低,变化区间范围由5~13 bit缩小至3.5~11.5 bit。

图3 最大拉伸值的实验记录结果
综上可知,在混合模型作用下,云平台资源的最大拉伸数值会明显增大,对于扩大云主机的数据信息存储能力具有较强促进作用。
表1 记录了实验组、对照组云平台资源最小压缩值及理想数值的实际变化情况。
分析表1 可知,实验组最小压缩值、对照组最小压缩值、理想数值均保持相同的物理变化趋势。从平均量角度来看,实验组的变化区间为[0.200 bit,0.317 bit],对照组的变化区间为[0.5 bit,0.8 bit],理想数值的变化区间为[0.31 bit,0.45 bit],其变化区间大小顺序为实验组<理想组<对照组。

表1 最小压缩值的实验记录结果
综上可知,在混合模型作用下,云平台资源的最小压缩值会出现持续缩小的变化形式,这在一定程度上,可实现对云主机数据信息下限存储能力的有效促进。
4 结束语
与高斯负载型数据伸缩方法相比,新型弹性伸缩方法可在混合模型的作用下,通过定义初始定位条件,计算得到云数据优选残差加权量,且由于平台主机始终处于相对变化的发展趋势,资源数据的采集与融合结果可对弹性扩容与伸缩扩容条件提供有效的保障。从实用性角度来看,混合模型支持下,云平台主机的最大拉伸值结果更大,最小压缩值结果更小,可在实现云资源数据与平台主机存储条件最大化匹配的同时,确保云服务质量水平的可行性,具备较强的实际应用价值。

