短基线无源多站时差定位精度分析及快速计算方法
蔡春霞,王堃,成章,江 威
(电子信息控制重点实验室,四川成都 610036)
无源时差定位由于具有隐蔽性强、定位精度高、易组网实现、对宽带低谱密度信号适应能力强等优点,近年来在军事领域被广泛应用[1-5]。文献[6-11]指出,多站时差定位中影响定位精度的因素有布站形式、基线长度、时差测量误差、站址测量误差等,并指出当构型形式一定时,基线越长,定位精度越高;时差测量误差越小,定位精度越高;站址测量误差越小,定位精度越高。但这些结论仅是定性地给出了规律,没有给出参数变化量对定位精度变化的定量分析。
文中基于无源多站时差定位数学模型,先对定位精度影响因素进行理论分析,然后针对短基线远距离定位场景,对时差测量误差、站址测量误差进行了定量分析,并给出了几何精度因子(Geometric Dilution Of Precision,GDOP)的快速计算方法,最后通过实例仿真比较了快速计算GDOP与理论GDOP之间的误差。
1 无源多站时差定位数学模型
与文献[6-15]相同,假设无源多站时差定位系统由一个主站和N(N≥3)个辅站组成。在三维空间直角坐标系中,各站的坐标为(xi,yi,zi),i=0,1,…,N,其中i=0 表示主站。目标辐射源的坐标为(x,y,z),结合工程实际,引入WGS-84 地球模型,则有如式(1)所示的双曲线定位方程组,求解方程组即可得到辐射源位置。

2 无源多站时差定位精度分析
对式(1)方程组两端求全微分可得:
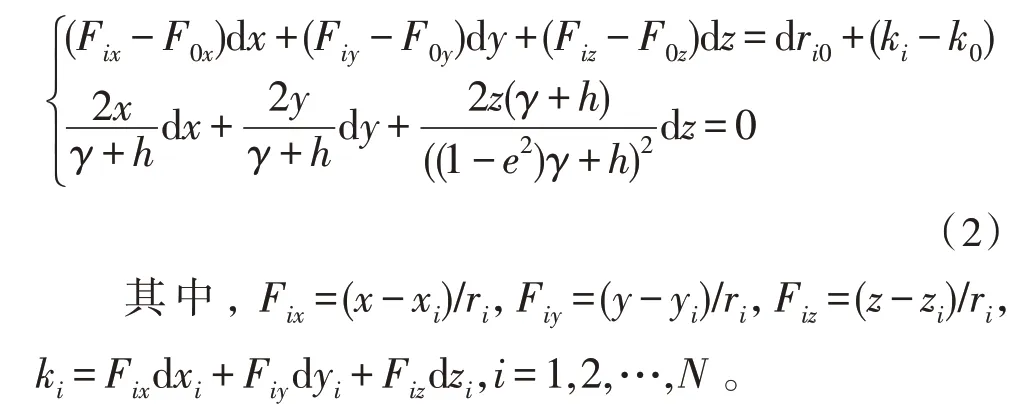
将式(2)写成矩阵形式得FdX=dR+dS,在系数矩阵F满秩的情况下,由最小二乘法得到dX=(FTF)-1FT(dR+dS),其中F表征各测量站相对于目标位置的方向余弦,与目标位置和布站形式有关:

dX=[dx,dy,dz]T表征定位误差;dR=[dr10,…,drN0,0]T=c[dτ10,…,dτN0,0]T=cdT表征距离差测量误差或者TDOA 测量误差;dS=[k1-k0,…,kN-k0,0]T表征站址测量误差。
由于距离差测量误差与站址测量误差相互独立,则定位误差的协方差矩阵为:
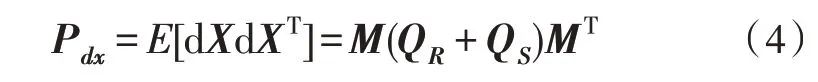
式中,M=(FTF)-1FT,QR=E[dRdRT] 为距离差测量误差的协方差矩阵,QS=E[dSdST] 为站址测量误差的协方差矩阵。将Pdx代入GDOP=可得定位精度。
下面着重分析在短基线远距离定位场景下,TDOA 测量误差、站址测量误差对GDOP 的影响。假设各测量误差经系统修正后是零均值的,站址误差在每次测量过程中的标准差保持不变,且站址误差各元素之间以及各站址误差之间不相关。
2.1 计算距离差测量误差的协方差矩阵QR
设是距离差测量误差方差,是TDOA 测量误差方差,ηij为dτi0与dτj0之间的相关系数,当i≠j时取ηij=0,则有:
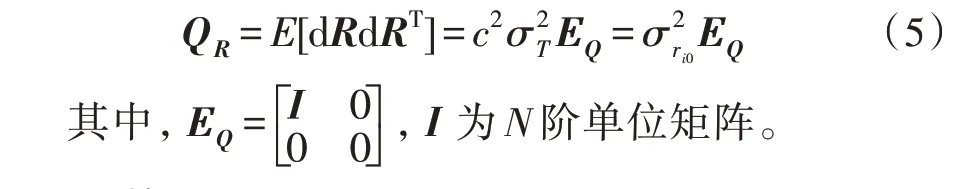
2.2 计算站址测量误差的协方差矩阵QS

在短基线远距离定位构型中,当i≠j时,各定位站到辐射源的距离近似相等,即r0≈ri≈rj,又主站和辅站i之间的距离ri0与主站到辐射源的距离r0相比非常小,即:

可用绝对位置误差协方差矩阵QAS和相对位置误差协方差矩阵QBS表示QS:
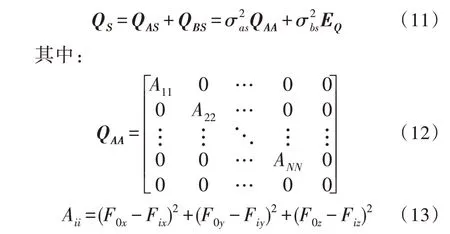
由式(5)、(11)可得,在短基线远距离定位场景中,若考虑主站和辅站之间的相对位置误差时,定位误差的协方差矩阵为:

综上可知,绝对位置误差对GDOP 的影响远小于时差测量误差和相对位置误差对GDOP 的影响,GDOP 与时差测量误差、相对位置误差均近似呈线性关系。在短基线远距离定位工程应用中,由于项的,且绝对位置误差σas不超过百米量级,因此项对GDOP 的贡献很小,可以忽略。
3 GDOP定量分析及快速计算方法
若定位构型不变,则与位置有关的参数和矩阵F、M、QAA等均为定值。在短基线远距离定位场景中,忽略绝对位置误差,则有记常数矩阵MEQMT为PEQ,此时GDOP 可表示为:
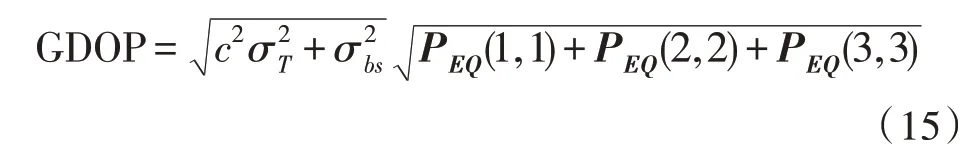
在式(15)的基础上进行推导,可得式(16)所示的GDOP 的快速计算公式。当TDOA 测量误差变化ΔT、相对位置测量误差变化Δσbs后,根据式(16)可快速得到新的定位精度GDOP'。
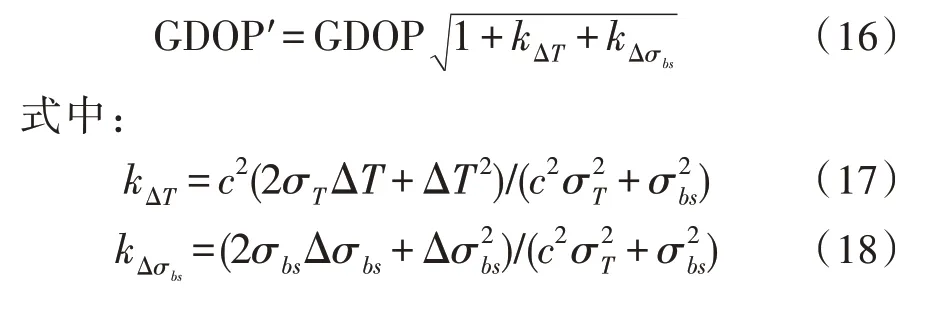
4 仿真分析
下面通过仿真分析,比较使用快速计算公式得到的GDOP 与理论GDOP 的误差。
文献[13-19]指出,在四站时差定位中要获得最佳精度的构型为T/Y 构型或者倒T/Y 构型,针对远场目标,在时差定位体制下,在二维平面中,辅站传感器在以主站传感器为圆心,某固定值为半径的圆上均匀分布时定位误差可达最小;在三维空间中,辅站传感器在以主站传感器为圆心,某固定值为半径的圆球上均匀分布。因此,不失一般性,下面以四站时差定位为例,定位构型取为等边倒Y 构型,如图1(a)所示,三个辅站在以主站为圆心,基线长度D为半径的圆上均匀分布,呈倒Y 结构。
定位精度算法在地心直角坐标系下进行运算,需要将东北天坐标系的ENU 坐标转换到地心直角坐标系下的三维直角坐标。不失一般性,取主站经纬高坐标为(90°,30°,50 km),如图1(b)所示,在ENU坐标系下,基线长度D=5 km,主站到目标的投影距离L0=300 km,投影高H=50 km。

图1 等边倒Y定位构型
仿真一:改变TDOA 测量误差初值σT0及其误差变化量ΔT
参数设置如表1 所示,TDOA 测量误差初值σT0范围为[5 10∶10∶40]ns,误差变化量ΔT范围为[0∶5∶100]ns,绝对位置误差σas取30 m,相对位置误差σbs取1 m。
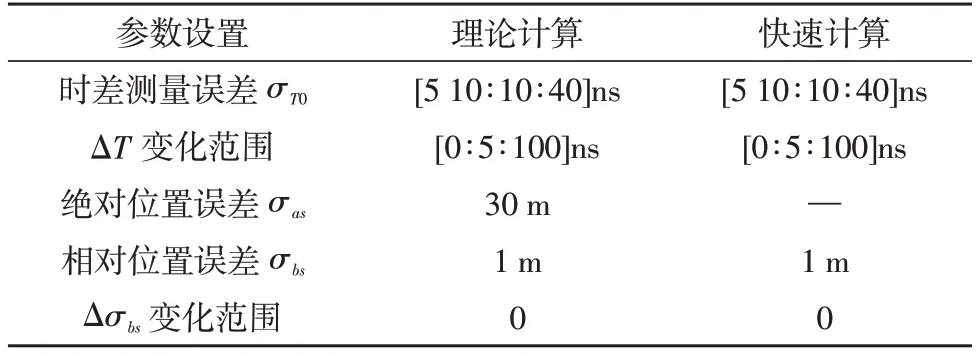
表1 仿真一参数设置
根据式(14)可得理论GDOP 仿真结果如图2 所示,根据式(16)可得快速计算的GDOP 仿真结果如图3 所示,两者差值如图4 所示,两者差值/理论GDOP 的比例如图5 所示。

图2 理论GDOP(改变σT0 和ΔT)
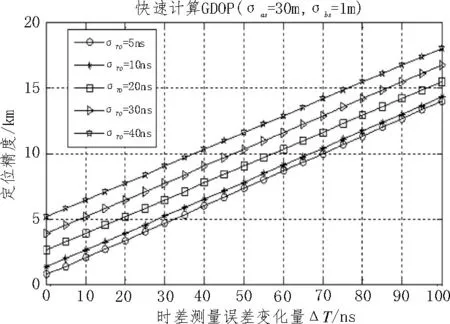
图3 快速计算GDOP(改变σT0 和ΔT)
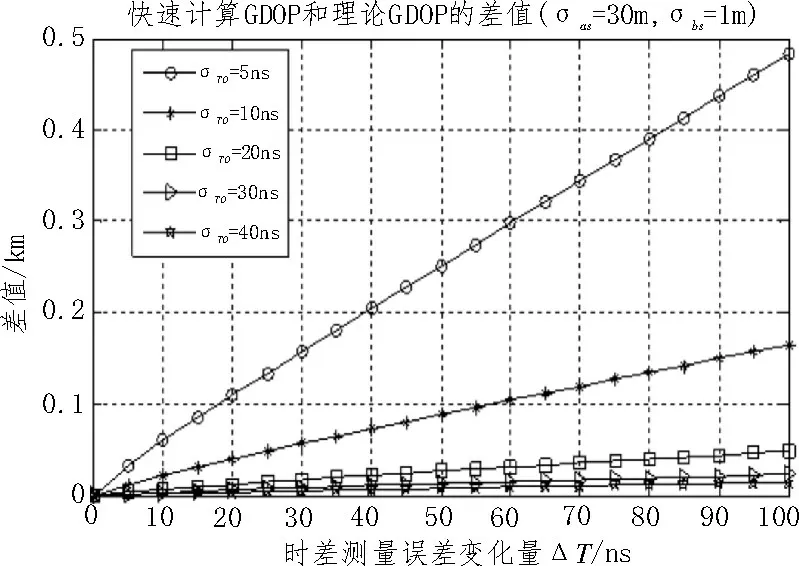
图4 快速计算GDOP与理论GDOP的差值(改变σT0 和ΔT)
从图2 可以看出,TDOA 测量误差与GDOP 近似呈线性关系,和前文公式推导的结论一致。从图5可以看出,初值σT0越大,快速计算GDOP 与理论GDOP 的误差越小,当σT0≥5 ns时,误差小于4%;当σT0≥20 ns时,误差小于0.3%。

图5 两者差值与理论GDOP的比例(改变σT0 和ΔT)
仿真二:改变相对位置误差初值σbs及其误差变化量Δσbs
参数设置如表2 所示,TDOA 测量误差σT取30 ns,绝对位置误差σas取30 m,相对位置误差初值σbs范围为[1 5 10 20 30]m,误差变化量Δσbs范围为[0:5:50]m。

表2 仿真二参数设置
根据式(14)可得理论GDOP 仿真结果如图6 所示,根据式(16)可得快速计算的GDOP 仿真结果如图7 所示,两者差值如图8 所示,两者差值/理论GDOP 的比例如图9 所示。
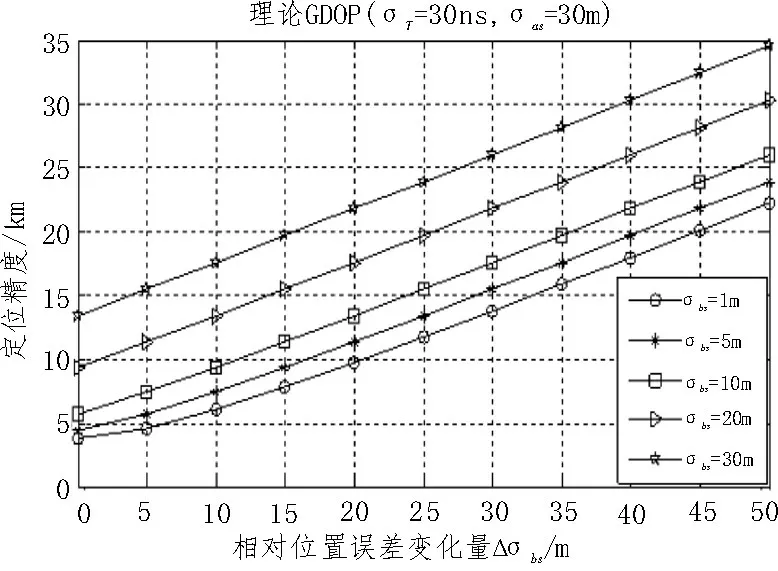
图6 理论GDOP(改变σbs 和Δσbs)
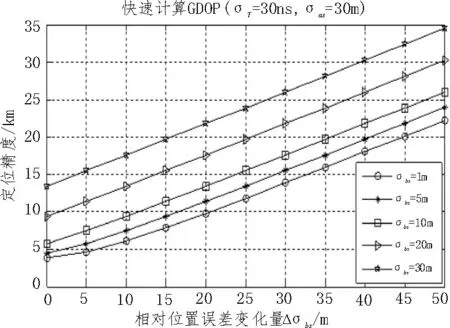
图7 快速计算GDOP(改变σbs 和Δσbs)

图8 快速计算GDOP与理论GDOP的差值(改变σbs 和Δσbs)
从图6 可以看出,相对位置误差与GDOP 近似呈线性关系,和前文公式推导的结论一致。从图9 可以看出,初值σbs越大,快速计算GDOP 与理论GDOP的误差越小,当σbs≥1 m时,快速计算GDOP 的误差小于0.2%。

图9 两者差值与理论GDOP的比例(改变σbs 和Δσbs)
以上的定量分析和仿真结果均考虑了主站和辅站之间的相对位置误差,如果不考虑主站和辅站之间的相对位置误差,那么站址测量误差协方差矩阵为:

对应的定位误差的协方差矩阵为:
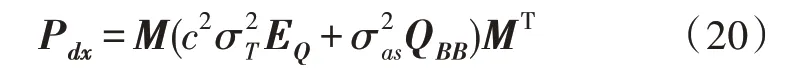
在相同的仿真条件下,比较有无考虑主站与辅站之间的相对位置误差对GDOP 的影响。仿真参数设置如表3 所示,计算结果也在表3 中给出,考虑σbs时的GDOP为3.89 km,不考虑时的GDOP为13.60 km,可以看出,前者定位精度远优于后者。

表3 有无考虑相对位置误差时的仿真参数设置及对应的理论GDOP结果
在不考虑主站与辅站之间的相对位置误差时,对应的GDOP 快速计算公式如式(21)所示,因为没有忽略任何项,所以其理论GDOP 和快速计算GDOP一致。
当TDOA 测量误差变化ΔT、绝对位置测量误差变化Δσas后,可得:

5 结论
基于无源多站时差定位数学模型,分析了定位精度的各个影响因素,针对短基线远距离定位场景,给出时差测量误差、站址测量误差对GDOP 精度影响的定量分析及对应的快速计算方法,可以快速计算出参数变化后的GDOP。
通过实例仿真可知,在考虑主站与辅站之间相对位置误差的情况下,当TDOA 测量误差初值为5 ns时,快速计算的误差小于4%;当TDOA 测量误差初值在20 ns 以上时,快速计算的误差小于0.3%;当相位位置误差σbs≥1 m时,快速计算GDOP 的误差小于0.2%。
由于快速计算的误差很小,在实际工程应用中,尤其是在试验外场等不具备仿真环境又必须根据现有的定位构型快速得到改变时差测量误差或站址测量误差后的定位精度时,快速计算得到的GDOP 有重要的指导意义。
此外,通过仿真比较可知,考虑主站与辅站之间的相对位置误差时的GDOP 远优于不考虑时的GDOP。同时给出了在不考虑主站与辅站之间的相对位置误差时的GDOP 快速计算方法。在工程条件允许时,推荐考虑主站与辅站之间的相对位置误差,可获得更高的定位精度。

