基于Beta-Negative Binomial的膨胀分布推广及应用
——以新冠病毒肺炎感染人数为例
李春玉,安博文,王浩东,牛丽娜
(1.河北经贸大学 数学与统计学学院,河北 石家庄 050061;2.华侨大学 经济与金融学院,福建 泉州 362021;3.新疆理工学院 理学院,新疆 阿克苏 843000)
新型冠状病毒肺炎现存确诊人数是评估疫情发展形势的重要指标,对于我国疫情防控工作开展具有重要意义.关于新冠病毒肺炎确诊人数的研究多集中在传播和预测方面.严阅等[1]率先基于时滞动力学系统建立新冠病毒传染病动力学模型,通过反演模型参数模拟了湖北省疫情的发展趋势.白宁等[2]根据湖北省疫情发展相关数据建立动力学模型,并通过MCMC 算法估计得到相关参数,对湖北省未来疫情的发展趋势作出评估预测.林秋实等[3]结合湖北省确诊病例的协变量信息,采用双重稳健模型对缺失数据进行填补,提高了动力学模型的估计预测精度.黄森忠等[4]基于SEIR 模型厘清了新冠疫情的流行病学基本参数,评估了疾控策略的效率.王霞等[5]构建了离武汉较近城市的新冠疫情传播网络模型,分析了武汉及周边地区复工复产的可能时间点.郭尊光等[6]基于反应扩散方程采用最小二乘法估计得到新冠病毒传染率,发现累计确诊人数会随传染率和扩散速率的增大而逐渐增加.丁志伟等[7]基于Back-projection模型推算得到我国部分地区新冠病毒肺炎的感染曲线,并给出了每日新增感染人数的期望值和置信区间.
在考察新冠疫情的传播途径与速度之余,充分了解当前现存确诊人数的分布状况也同等重要.Ali等[8]首次将Poisson 分布引入传染病人数研究中,白永昕等[9]构造慢性病发病率和风险差时将传染病确诊人数假定服从Poisson 分布,王维贤等[10]也基于Poisson 分布构造了慢性病相关差的置信区间.Poisson 分布是Negative Binomial 分布的极限分布, 意思就是在样本量巨大的情况下,NegativeBinomial 分布与Poisson 分布是渐进等价的[11].当考察我国34 个地区新冠病毒肺炎确诊人数的分布情况时,样本量为34,样本量较少,此时假定现存确诊人数服从Poisson 分布不免出现偏差,因此需要采用更为合适的Negative Binomial 分布.田茂再等[12]基于Negative Binomial 分布构造了发病率的置信区间,并且模拟效果良好.之前学者研究新冠疫情的感染率时发现,确诊病例的感染率不尽相同,意味着Negative Binomial 分布中的感染率参数p 不再是一个恒定不变的常数,而可能是一个服从某种统计分布的随机变量.借鉴Lee 等[13]和Wang 等[14]的研究思路, 假定感染率p 服从Beta 分布, 那么现存确诊人数便服从Beta-Negative Binomial 分布,本文就基于Beta-Negative Binomial 分布展开研究.
与此同时,考虑到我国疫情防治工作效果明显,部分地区现存确诊人数持续为0 或持续为1,而且这样的地区占比较高,这种情况与Lambert 等[15]提出的0 膨胀分布十分相近,也与Melkersson 等[16]提出的0-1 膨胀分布非常相近.从目前我国34 个地区现存确诊人数的样本数据来看,现存确诊人数可近似看作一种膨胀分布.可将现存确诊人数假定服从0 膨胀Beta-Negative Binomial 分布,也可将现存确诊人数假定服从0-1 膨胀Beta-Negative Binomial 分布,对于分布中的参数可以借助EM算法进行求解.Zhang 等[17]采用极大似然估计下的Fisher 信息矩阵和EM算法估计了0-1 膨胀分布的参数;Tang 等[18]借助隐变量写出了0-1 膨胀的似然函数,并基于EM算法给出了参数的极大似然估计值,肖翔[19]又在此基础上提供了0-1 膨胀参数估计的EM算法和M-H 抽样算法.
综合之前学者的研究成果,本文将基于Beta-Negative Binomial 分布研究我国34 个地区新冠病毒肺炎现存确诊人数的分布情况.本文其余部分的布局如下:第1 部分依次构建基于Beta-Negative Binomial的新冠肺炎感染人数分布、基于0 膨胀Beta-Negative Binomial 的新冠肺炎感染人数分布和基于0-1 膨胀Beta-Negative Binomial 的新冠肺炎感染人数分布;第2 部分对构建的3 种分布进行参数估计,并给出拟合分布相对最优的检验方法;第3 部分对理论结果进行数值模拟,分析估计算法的收敛性与精度;第4 部分对我国2021年1月1日~6日的新冠肺炎感染人数分布情况进行拟合;第5 部分给出研究结论.
1 分布构建
本部分针对新冠病毒肺炎现存确诊人数构建以下3 种分布,分别为:基于Beta-Negative Binomial 的新冠肺炎感染人数分布(简记为BNB 分布)、基于0 膨胀Beta-Negative Binomial 的新冠肺炎感染人数分布(简记为ZIBNB 分布)以及基于0-1 膨胀Beta-Negative Binomial 的新冠肺炎感染人数分布(简记为ZOIBNB 分布).
用X 表示单个人的新冠病毒肺炎感染概率,当现存确诊人数Y 服从Negative Binomial 分布时,则有YNB~NB (r ,x ),其概率质量函数为

随着现存确诊人数变动的复杂化,单一的Negative Binomial 分布并不能全面揭示全国34 个地区现存确诊人数的分布状况.若假设单个人肺炎病毒感染概率X 服从Beta 分布,即X~Beta(α,β),则对应的概率密度函数为

此时,现存确诊人数Y 便服从具有分层性质的离散分布,即Beta-Negative Binomial 分布,记为~BNB (r ,α,β),根据式(1)和式(2)可以写出Y 与X 的联合质量函数,为

通过对式(3)中的X 从0 到1 积分便可得到现存确诊人数YBNB的概率质量函数,为

为刻画较多地区现存确诊人数为0 的情况,参考Tang 等[18]的研究方法,引入隐变量B~B(1,p ),令YZIBNB=YBNB(1−B),则现存确诊人数Y 便服从0 膨胀Beta-Negative Binomial 分布,记为YZIBNB~ZIBNB (r,α,β,p ),其中p 表示0 膨胀参数,概率质量函数为
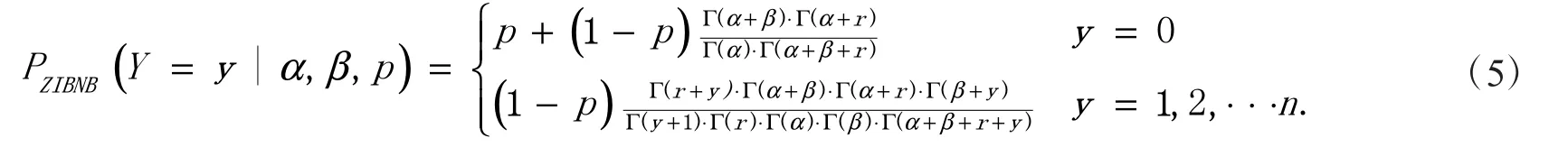
式(5)的具体证明过程可仿照文献[20]中定理1 的证明.
为进一步刻画部分地区现存确诊人数为1 的情形, 因此在0 膨胀Beta-Negative Binomial 分布的基础上再引入隐变量C~B(1,q ),令YZOIBNB=YZIBNB+B(1,−C)则现存确诊人数便服从0-1 膨胀Beta-Negative Binomial 分布,记为YZOIBNB~ZOIBNB (r,α,β, p ,q ),其中q 表示1 膨胀参数,概率质量函数为

式(6)的具体证明过程可仿照文献[20]中定理2 的证明.下面将对本节建立的3 种分布进行参数估计.
2 参数估计
2.1 点估计
假设有n个地区,现存确诊人数的数据结构为y=(y1,⋅⋅⋅,yn),决定0膨胀的隐变量B 数据结构为b=(b1,⋅⋅⋅,bn),决定1膨胀的隐变量C数据结构为c=(c1,⋅⋅⋅,cn),这里采用极大化似然法依次对上述3种分布的参数进行估计.
基于Beta-Negative Binomial 的新冠肺炎感染人数分布的对数似然函数为
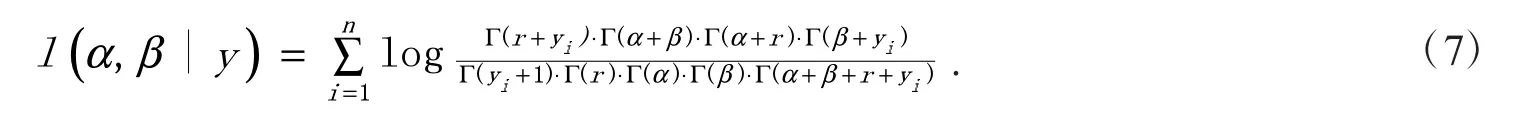
由极大似然估计原理可知,式(7)最大化下的估计值α和β即为方程组(8)的解.

式(8)中:ψ(•)表示对数伽马函数的导数,即.经过后续的数值模拟发现,与同类计算非线性方程组的迭代算法比较(例如Newton-Raphso 迭代),不动点迭代更适用于求解式(8),因此这里采用不动点迭代计算式(8)的数值解.对式(8)进行等价变形,有

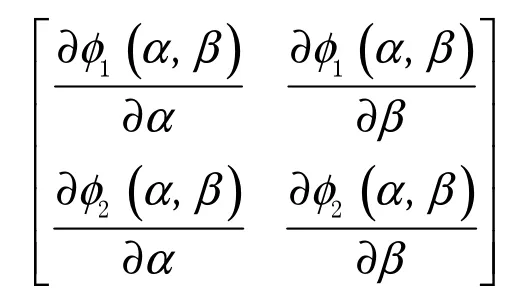
的谱半径.由不动点定理可知,当谱半径ρ(φ′ ) <1时,式(8)具有收敛的数值解,由此可以得到λ的取值.
最终计算出的数值解表示为

式中t 表示迭代次数.
基于0 膨胀Beta-Negative Binomial 的新冠肺炎感染人数分布的对数似然函数为

式(9)中含有隐变量,因此采用EM算法求解似然的最大化.E 步计算隐变量B 的期望,为

式中隐变量B 数学期望的具体计算过程详见文献[20]中命题1 的证明.M 步计算似然函数最大化,式(9)最大化下的估计值α、β和 p分别为方程组(10)和方程(11)的解.


由式(11)解得

式(10)的求解方法与式(8)同理,最终的数值结果表示为

式中t 表示迭代次数.
基于0-1 膨胀Beta-Negative Binomial 的新冠肺炎感染人数分布的对数似然函数为
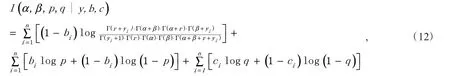
式(12)中含有隐变量,因此采用EM 算法求解似然的最大化.E 步计算隐变量B 和隐变量C 的期望,为

式中隐变量B与隐变量C 数学期望的具体计算过程详见文献[20]中命题2 的证明.M 步计算似然函数最大化,式(12)最大化下的估计值α、β、p和 q分别为方程组(13)和方程(14)的解.
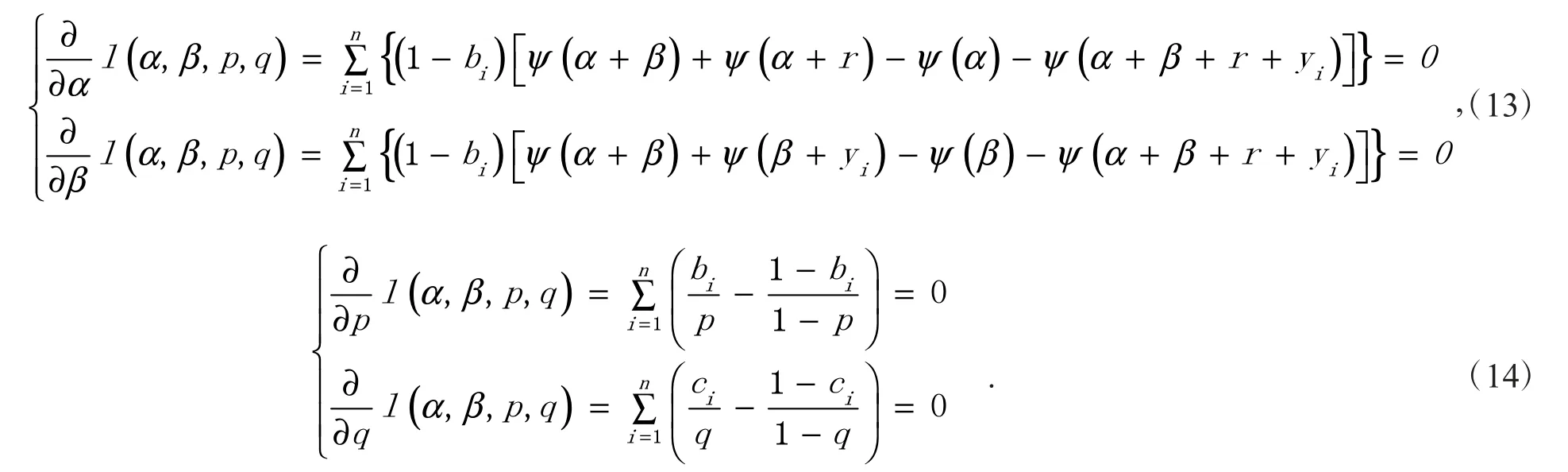
由式(14)解得

式(13)的求解方法与式(8)同理,最终的数值结果表示为

式中t 表示迭代次数.
2.2 置信区间构造
2.1 中计算出了分布参数的点估计值,由此可以分别写出3 种分布不含隐变量的对数似然函数.用n0表示现存确诊人数为0 的地区个数,用 n1表示现存确诊人数为1 的地区个数,为了方便利用Matlab 编程计算,分别记
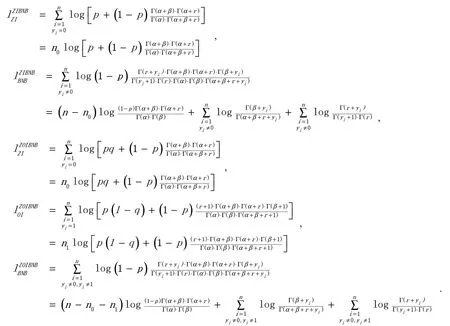
基于Beta-Negative Binomial 的新冠肺炎感染人数分布的对数似然函数为

基于0 膨胀Beta-Negative Binomial 的新冠肺炎感染人数分布的对数似然函数为

基于0-1 膨胀Beta-Negative Binomial 的新冠肺炎感染人数分布的对数似然函数为

用l*表示各个分布的对数似然函数,依次取为lBNB、lZIBNB和lZOIBNB,使用Matlab 软件分别计算3 种分布对数似然函数对参数的二阶偏导,进而求得3 种分布对应的Fisher 信息矩阵.考虑如下形式的Fisher信息矩阵,将第(假设所有参数个数为 k,则i= 1,⋅⋅⋅,k)个参数 oi对应的Fisher 信息矩阵记为,其中,

由此,可以计算出回归系数 oi的方差为
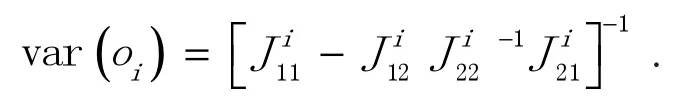
从而,回归系数 oi的(1−α)置信区间为

式(15)中:zα2表示标准正态分布的分位点.
2.3 分布比较
本文构建了3 种新冠肺炎感染人数的分布,在实际情况中仅需要选择一个相对最优分布解释现实问题.基于此,这里给出一种相对最优分布的比较办法.分布的比较原则为:当两个分布所含有的信息量差别不大时,分布参数越少则分布越优.分布的信息量可以通过似然函数进行反映,那么分布的比较就转化为似然函数差别的比较,因此构造似然比检验(LR 检验)统计量进行假设检验[11].
ZIBNB 分布与BNB 分布比较.原假设为两个分布的信息量差别不大,即选择BNB 分布;当拒绝原假设时,说明ZIBNB 分布所含信息量要远高于BNB 分布,即ZIBNB 分布.构造的LR 检验统计量为

其中,kZIBNB表示ZIBNB 分布的参数个数,kBNB表示BNB 分布的参数个数.
ZOIBNB 分布与BNB 分布比较.原假设为两个分布的信息量差别不大,即选择BNB 分布;当拒绝原假设时,说明ZOIBNB 分布所含信息量要远高于BNB 分布,即ZOIBNB 分布.构造的LR 检验统计量为

其中,kZOIBNB表示ZOIBNB 分布的参数个数.
ZOIBNB 分布与ZIBNB 分布比较.原假设为两个分布的信息量差别不大,即选择ZIBNB 分布;当拒绝原假设时,说明ZOIBNB 分布所含信息量要远高于ZIBNB 分布,即ZOIBNB 分布.构造的LR 检验统计量为

为了方便编程计算,分别记

则有

3 数值模拟
下面采用Matlab R2016a 编程进行数值模拟.
3.1 Beta-Negative Binomial 分布
产生40 个随机样本.假设地区数为n=40;生成单个人肺炎病毒感染概率X~Beta(4,9),再生成Negative Binomial 分布随机数Y~NB(8 ,x );最后生成现存确诊人数YBNB~BNB(8,4,9).将现存确诊人数YBNB和r=8作为已知条件进行参数估计,估计结果见表1.

表1 BNB 分布参数的数值模拟结果Tab.1 Numerical simulation results of BNB distribution parameters
表1数值模拟结果显示,当观测样本量为40 时,估计值的相对误差大小均控制在1%左右,且真实值都落入95%置信区间,说明估计精度较高.图1展示了参数估计值50 次迭代过程的轨迹图,可以发现,参数估计值均在迭代10 次之内收敛,说明估计结果的收敛性较强.
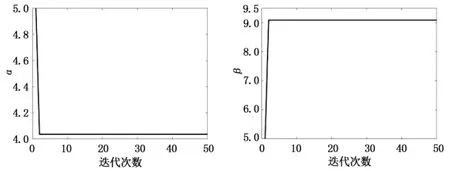
图1 BNB 分布参数估计的迭代轨迹图Fig.1 Iterative trajectory diagram for parameter estimation of BNB distribution
3.2 0 膨胀Beta-Negative Binomial 分布
产生40 个随机样本.在3.1 的基础上,生成决定0膨胀部分的隐变量B~B(1,0.3),进而生成现存确诊人数YZIBNB~ ZIBNB (8,4,9,0.3).将现存确诊人数YZIBNB和 r=8作为已知条件进行参数估计,估计结果见表2.

表2 ZIBNB 分布参数的数值模拟结果Tab.2 Numerical simulation results of ZIBNB distribution parameters
表2数值模拟结果显示,当观测样本量为40 时,估计值的相对误差大小均控制在5%以内,且真实值都落入95%置信区间,说明估计精度较高.图2展示了参数估计值50 次迭代过程以及隐变量估计值49 次迭代过程的轨迹图,可以发现,分布参数和隐变量的估计值均在迭代10 次之内收敛,说明估计结果的收敛性较强.

图2 ZIBNB 分布参数和隐变量估计的迭代轨迹图Fig.2 Iterative trajectory diagram for parameters and hidden variable estimatesof ZIBNB distribution
3.3 0-1 膨胀Beta-Negative Binomial 分布
产生40 个随机样本.在3.2 的基础上,生成决定1膨胀部分的隐变量C~B(1,0.4),进而生成现存确诊人数YZOIBNB~ZOIBNB (8,4,9,0.3,0.4).将现存确诊人数YZOIBNB和r=8作为已知条件进行参数估计,估计结果见表3.

表3 ZOIBNB 分布参数的数值模拟结果Tab.3 Numerical simulation results of ZOIBNB distribution parameters
表3数值模拟结果显示,当观测样本量为40 时,估计值的相对误差大小均控制在5%以内,且真实值都落入95%置信区间,说明估计精度较高.图3展示了参数估计值50 次迭代过程以及隐变量估计值49 次迭代过程的轨迹图,可以发现,分布参数和隐变量的估计值均在迭代20 次之内收敛,说明估计结果的收敛性较强.

图3 ZOIBNB 分布参数和隐变量估计的迭代轨迹图Fig.3 Iterative trajectory diagram for parameters and hidden variable estimatesof ZOIBNB distribution
4 新冠病毒肺炎感染人数的分布拟合
这部分对我国34 个地区2021年1月1日~6日新冠病毒肺炎现存确诊人数的分布状况进行拟合,样本数据来源于国家及各省、市、自治区卫健委,数据截止日期为2021年1月7日0 时.
4.1 样本数据描述
本文选取的数据指标为新冠病毒肺炎现存确诊人数(Y,单位:人),作出2021年1月1日~6日每一天的现存确诊人数分布状况,如图4所示.从1月1日~6日的数据比较来看,香港的现存确诊人数最多,湖北、新疆、江西、重庆、甘肃、海南、吉林、贵州、宁夏、澳门、青海和西藏的现存确诊人数持续为0,湖南、安徽和广西的现存确诊人数持续为1.其中,1月1日有13 个地区现存确诊人数为0,有3 个地区现存确诊人数为1,二者占比为47.06%;1月2日、3日、5日和6日有12 个地区现存确诊人数为0,有4 个地区现存确诊人数为1,二者占比为47.06%;1月4日有12 个地区现存确诊人数为0,有3 个地区现存确诊人数为1,二者占比为44.12%.我国34 个地区现存确诊人数中0 值和1 值占比较高,这也间接证明了构建膨胀分布描述现存确诊人数分布状况的必要性.

图4 2021年1月1日~6日现存确诊人数条形图Fig.4 Bar chart of the number of existing confirmed cases from January 1 to 6,2021
4.2 估计结果分析
假定新冠病毒肺炎现存确诊人数依次服从Beta-Negative Binomial 分布、0 膨胀Beta-Negative Binomial 分布和0-1 膨胀Beta-Negative Binomial 分布,根据前文推导的理论公式分别对3 个分布的参数进行估计,以下结果均采用Matlab R2016a 编程得到.
采用Matlab 计算数值解时发现,若假定现存确诊人数服从Beta-Negative Binomial 分布,Matlab 编程结果一直报错,这就意味着无法得到数值结果,说明不能找到Beta-Negative Binomial 分布对应的相关参数,即现存确诊人数不会服从Beta-Negative Binomial 分布,也就是说无法用Beta-Negative Binomial 分布描述现存确诊人数的分布状况.出现这一计算结果其实并不意外,从5.1 的数据结构分析中就可以了解到,每一日现存确诊人数中0 值和1 值的占比均超过40%,甚至其中有5 天时间现存确诊人数接近50%,因此需要用膨胀的Beta-Negative Binomial 分布进行拟合.当然这也是本文所作的主要工作,将Beta-Negative Binomial 分布推广到了0 膨胀Beta-Negative Binomial 分布和0-1 膨胀Beta-Negative Binomial 分布.
表4给出的是0 膨胀Beta-Negative Binomial 分布和0-1 膨胀Beta-Negative Binomial 分布的参数估计结果,并给出了这两种分布的比较检验结果.由LR 检验结果可知,每一日的LR 检验均在5%显著水平下拒绝原假设,即0-1 膨胀Beta-Negative Binomial 分布更适合描述我国新冠病毒肺炎现存确诊人数的分布状况.1月1日现存确诊人数服从ZOIBNB(8,1.22,2.54,0.46,0.84),1月2日现存确诊人数服从ZOIBNB(8,1.22,2.60,0.46,0.77),1月3日现存确诊人数服从ZOIBNB(8,1.38,3.33,0.46,0.76),1月4日现存确诊人数服从ZOIBNB(8,1.27,2.82,0.43,0.82),1月5日现存确诊人数服从ZOIBNB(8,1.42,3.79,0.47,0.76),1月6日现存确诊人数服从ZOIBNB(8,1.29,3.34,0.46,0.76).

表4 分布参数的估计结果Tab.4 Estimation results of distribution parameters
通过比较1月1日~6日的分布参数可以发现,决定肺炎感染概率的参数α和β变化最大,连续6 天α变动的标准差为8.32%、β变动的标准差为49.46%;决定1 膨胀的参数 q变化次之,连续6 天变动的标准差为3.56%;决定0 膨胀的参数 p变化最小,连续6 天变动的标准差为1.37%.由此可见,新冠病毒肺炎感染概率每日波动较大,但由于我国疫情防治工作一直有条不紊的开展,我国近一半地区现存确诊人数持续为0 或持续为1,且波动情况较小.
5 小结
本文将Beta-Negative Binomial 分布推广到0 膨胀Beta-Negative Binomial 分布和0-1 膨胀Beta-Negative Binomial 分布,分别构建新冠病毒肺炎现存确诊人数BNB 分布、ZIBNB 分布以及ZOIBNB 分布;采用EM算法给出分布参数的点估计值,此部分工作的重点在于M步选用了不动点迭代算法,之前学者多采用Newton-Raphso 迭代算法[20-21],但经过数值模拟发现,Newton-Raphso 迭代无法计算出最终结果,因此这里选用不动点迭代,使迭代算法更适用于本文所提到的3 个分布;基于Fisher 信息矩阵计算估计参数的方差,进而给出参数的区间估计值;基于LR 检验给出BNB 分布、ZIBNB 分布和ZOIBNB 分布中相对最优分布的遴选方法.通过数值模拟发现,本文给出的估计算法收敛性很强、精度较高.新冠病毒肺炎感染人数分布的拟合结果显示,ZOIBNB 分布更适用于描述我国34 个地区现存确诊人数的分布情况,通过比较2021年1月1日~6日现存确诊人数的分布参数发现,单个人的每日病毒感染率波动较大,我国有近一半地区现存确诊人数为0 或为1.

