基于机器学习的烟草生丝水分智能控制模型

史成云 崔文波 崔汝念 邹欣延

（红塔烟草（集团）有限责任公司昭通卷烟厂，云南 昭通 657000）

1 数据驱动预测控制框架

本研究从烟草制造企业生产过程执行管理系统中提取大量的历史实际生产与检测数据，结合机器学习相关算法、控制算法和参数设置经验，分析入口水分、出口水分和车间温湿度等可控影响因素与天气情况等不可控影响因素对烟草生丝水分造成的影响。利用相似度计算法筛选出合格的历史生产数据结果作为烟草生丝水分控制的参考标准，采用数据驱动的预测控制算法降低烟草生丝水分的误差控制范围，最终得到烟草生丝水分控制后的结果。

本框架采用多元非线性回归的机器学习算法[1]，从历史数据中学习加水量控制模型和出口水分预测模型，实际生产过程中由控制模型计算加水量，根据计算得到的加水量用预测模型预测出口水分，如果预测值满足工艺要求则采用计算值，否则使用优化函数寻找优化方向，再次计算加水量直到预测出口水分满足工艺要求。并根据一段时滞后监测到的实际出口水分数据作为反馈输入调整优化函数。模型框架如图1 所示。

图1

2 数据趋势分析

加水量和出口水分之间的数据趋势关系如图2所示。

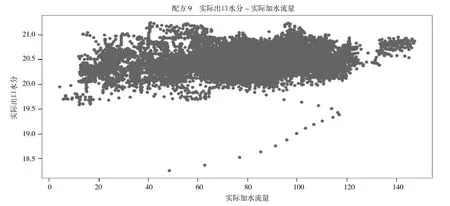
图2

从图2 可以看出，除部分离群点外，数据聚集为一个巨大的簇，特征之间没有明显的线性关系。考虑到实际生产过程中，烟叶生丝的含水率除了受到可控因素影响外，还受到不可控的诸如环境温湿度等的影响，是一个复杂的多正交系统[2]，针对这一数据特点我们采用多元非线性回归的方法构建水分预测模型和加水量计算模型，针对不同配方分别进行训练。

3 模型训练和评估

将历史数据按照配方号进行分割，采用2022 年8月1 日之后的数据进行训练（和现场工控工程师及数据采集人员交流，此时间后采集的数据较为稳定）。

3.1 水分预测模型

输入特征：’实际加水流量’，’加水瞬时量’，’加水累计量’，’实际热风温度’，’实际循环风温度’，’蒸汽累计量’，’蒸汽实际流量’，’蒸汽瞬时量’，’实际入口水分’，’环境温度’，’环境湿度’，’电子秤实际流量’，’电子秤累计量’，’电子秤瞬时量’。

输出：’实际出口水分’。

随机选取70%的数据作为训练数据，剩余30%的数据作为测试数据。经过多次迭代拟合阶次为5 时模型决定系数超过0.99，拟合效果可以接受。（如图3）

图3

3.2 加水量计算模型

输入特征：’实际出口水分’，’加水瞬时量’，’加水累计量’，’实际热风温度’，’实际循环风温度’，’蒸汽累计量’，’蒸汽实际流量’，’蒸汽瞬时量’，’实际入口水分’，’环境温度’，’环境湿度’，’电子秤实际流量’，’电子秤累计量’，’电子秤瞬时量’。

输出：’实际加水流量’。

随机选取70%的数据作为训练数据，剩余30%的数据作为测试数据。经过多次迭代拟合阶次为5 时模型决定系数超过0.99，拟合效果可以接受。（如图4）

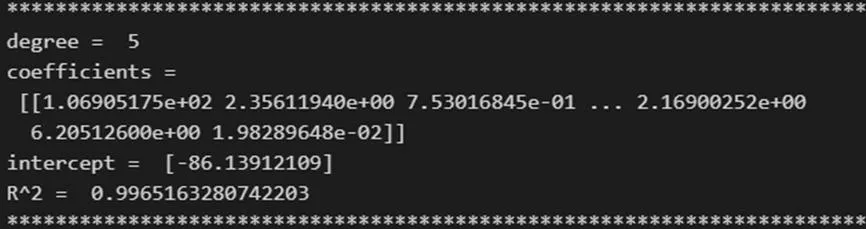
图4

3.3 判定函数

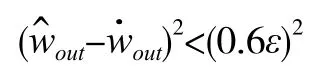
3.4 优化函数

烟叶从经过电子秤到出口有时滞，PID 设备和传感器的采集频率为每2 秒1 次，PID 设备读数和传感器检测值不可避免地存在误差[4]，从数据看误差表现出不稳定性，这和烟叶生丝生产过程中受到多种因素综合影响的认识是一致的，为了更好地对加水量进行优化，我们采取一段时滞后的出口水分平均值作为优化依据。

目标优化函数：

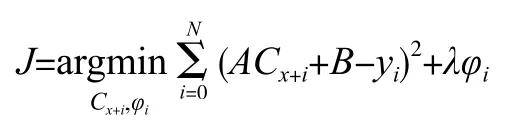
Cx+i表示时滞内的加水总量，yi表示时滞内的出口水分平均值，φi≥0 表示天气等不可控因素，λ表示不可控因素在模型中的权重[5]。h=ACx+i+B令代入上式可得：

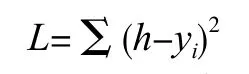
对函数L 求导，当导数为0 时取得最小值：

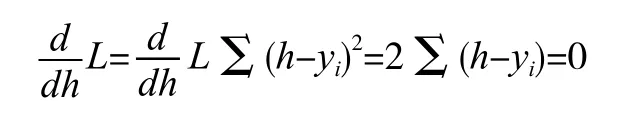
利用最小二乘法对目标优化函数J中的∑(ACx+i+Byi)2求解。

3.5 模型结果分析

使用设备改造完成后30%的数据量作为测试数据，分别对加水量计算模型和出口水分预测模型进行测试，依据平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和均方根误差（RMSE）三个指标进行评 估。MSE 值≤0.045，MSAE 值≤0.029，RMSE 值≤0.062，满足工艺要求。出口水分预测和真实值对比图如图5 所示。

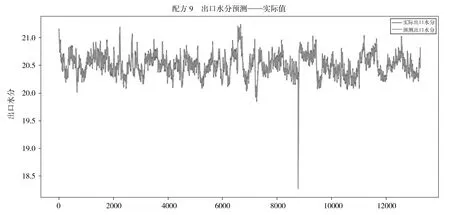
图5

从图5 中可以看出，模型从现有数据中很好地习得了历史数据中的加水经验，并可以较为准确地预测给定加水参数条件下的出口水分。