应急情况下供应商的理想订购与转运方案

陈云露，黄豪杰，虞辰洋，张海良

（台州学院 电子与信息工程学院，浙江 临海 317000）

0 引言

一家企业生产需多种原材料，每年生产总时间t周，需提前t周制订原材料的订购和运输计划。在满足企业基本生产和经营条件情况下分析相关数据，对以下3个问题展开讨论：

1.结合给定数据，对402个供应商的供货特点进行量化分析，建立一个能反映保障企业生产重要程度的数学模型，得出企业最主要的50个供应商。

2.结合给定数据，以满足生产需求为目标选择最少供应商。以最经济为目标，决策未来t周原材料的订购计划。基于原材料订购计划，满足在损耗量最小的情况下，制订相应的转运方案并分析它们的实施效果。

3.为降低生产成本，企业增加某类原材料、降低另一类的采购量，在满足降低运输存储成本和减少转运损耗率两个目标的前提下，建立全新订购和转运方案模型并分析其实施效果。

1 模型的建立与求解

1.1 供应商选择的模型建立与求解

1.1.1 供应商供货特征的量化分析过程与结论

对402个供应商供货进行量化分析，将供货特点分为4类：持续供货能力、供货能力承载度、供货可靠性和供货选择性。

持续供货能力：根据给定数据统计供应商供货量的持续周数，发现其中35家供应商在240周内可以连续供货，其余大多只能持续5～8周。

供货能力承载度：由给定数据计算每个供应商单周最大供货量，发现单周最大的供货量主要集中在1 m3到1 601 m3，零散分布区间大，最大值为36 972 m3，最小值为1 m3。

供货可靠性：将供应商供货量和企业订货量的商定义为供货满足率，观察分布规律后发现供货满足率0～0.1为第一类，0.1～0.2为第二类，0.3～0.4为第三类，0.5～0.6为第四类，0.7～1.37为第五类，其中第五类占比最大。

供货选择性：分析得知3大类原材料A、B、C的供应商分别为A类146家、B类134家、C类122家。

1.1.2 基于熵权法的TOPSIS模型的建立与求解

结合供应商供货特点得出影响企业生产重要性的供货满足率等14个指标，如表1所示。

表1 14个指标说明表

预处理数据：模型既能保障企业生产又明晰了m个供应商的重要性。根据影响企业生产重要性确定n个指标，针对m个供应商计算第m个供应商的第n个指标的指标值xij(i=1,2,3,...,m;j=1,2,3,...,n)，结合指标值xij构造初始决策矩阵A=(xij)m×n，即

标准化处理：影响企业生产重要性的n个指标存在正反向指标，所以需要对矩阵A=(xij)m×n进行标准化处理，得到标准化矩阵B=(yij)m×n，即

指标好坏判断标准如下：

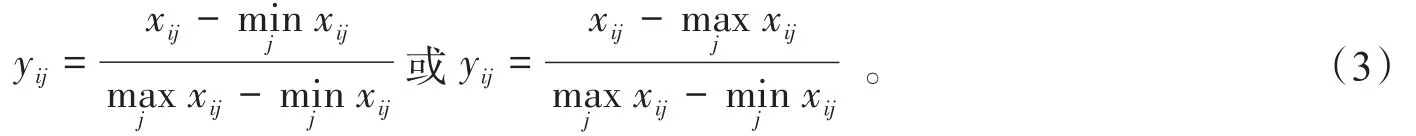
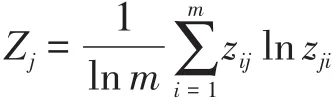
确定熵权：n个指标的熵权wj为

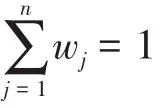
加权计算：由熵权法确定的权重和标准化矩阵B=(yij)m×n相乘可得到一个加权标准化矩阵C=(cij)m×n，cij=yij×wj，其中，wj是熵权法确定的权重。

正负理想解：加权标准化矩阵C=(cij)m×n将正向指标j+的最大值和负向指标j-的最小值构造后得到正理想解M+；将正向指标的最小值和负向指标的最大值构造后得到负理想解M-。即

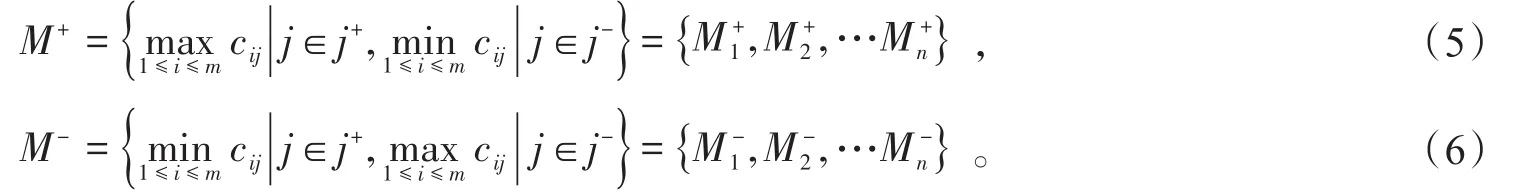
402个供应商重要程度到正负理解的欧氏距离如下：

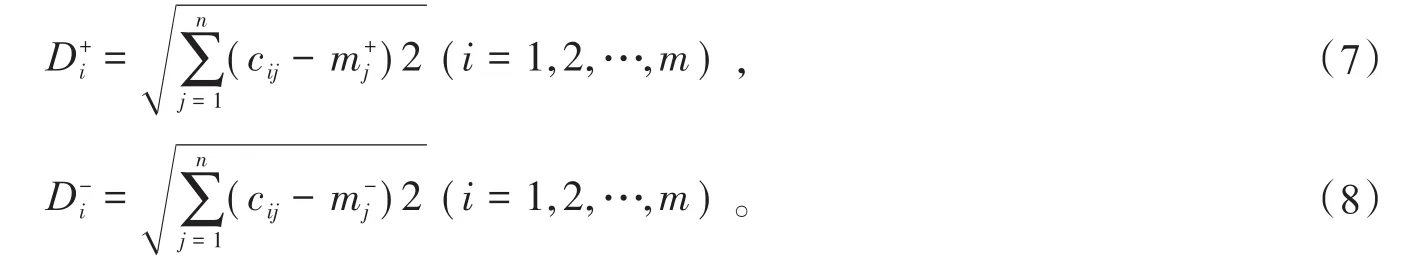
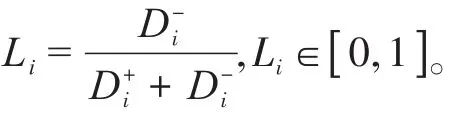
1.1.3 基于熵权法的TOPSIS模型求解结论

结合供应商的供货特点计算影响企业生产重要性的14个指标的指标值。利用熵权法将原始指标值数据进行归一化处理，应用公式（4）得到每个指标的熵权，如表2所示。

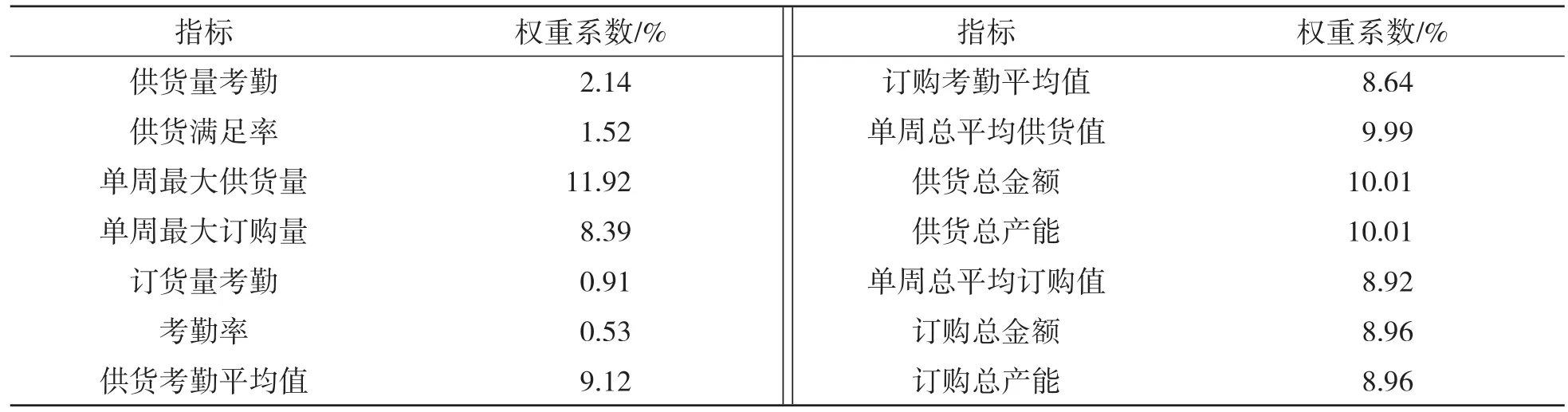
表2 14个指标的权重表

相对贴近度越接近1排名越高，由排名的高到低筛选最主要的50家供应商，结果如表3所示。

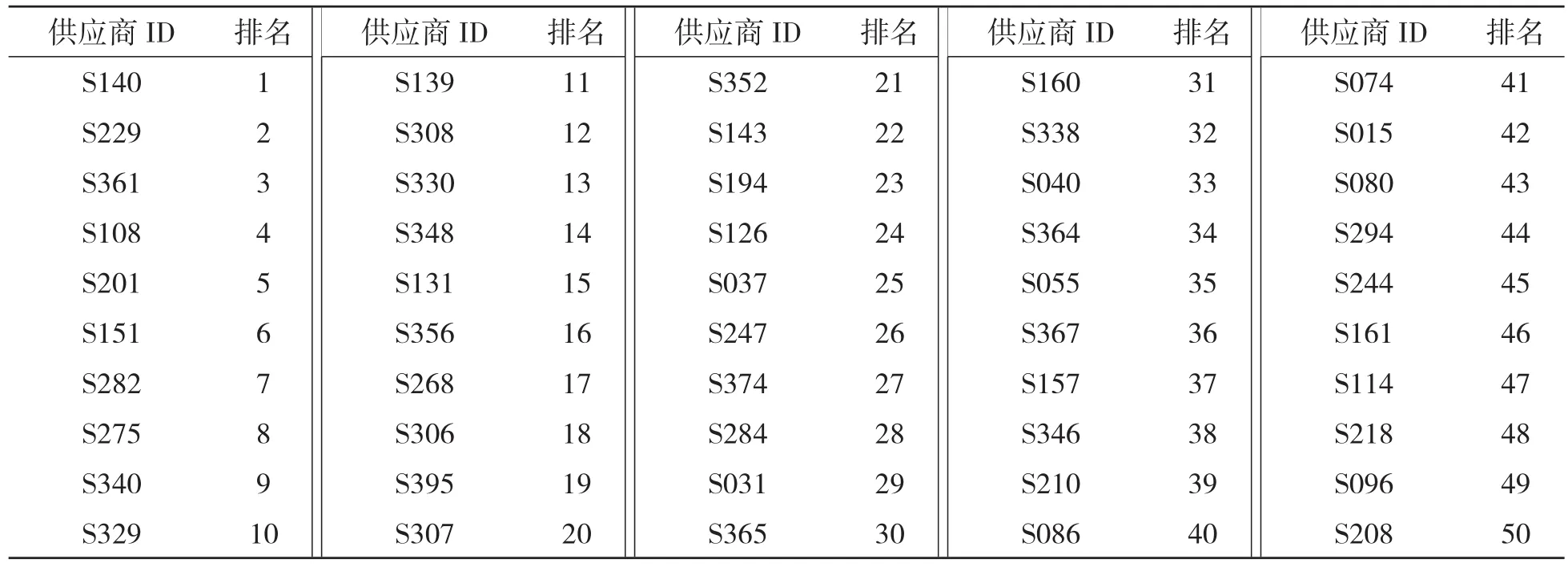
表3 50家最主要的供应商

1.2 正常生产的模型建立与求解

1.2.1 一般线性规划模型的建立与求解

结合筛选后的50家重要供应商，将正常生产需求问题分为3个规划问题和1个实施效果检测问题。一是在订购量满足“两周原材料库存大于生产量”和“每周产能为2.82万m3”的前提下，求出最少供应商的数量。二是制订一个花费成本最低的订购计划，并设置如下规定［3］：将损耗率设为平均值2%，第1周企业订购量为5.755万m3，第2～24周为2.878万m3。

接着对50家主要供应商再进行筛选，将最大订货量排名靠前、持续供货能力强而供货频率高的应急供应商放置在第1周，以应对订购量翻倍的突发情况，第2～24周安排长期合作供应商。车辆配送安排：第1周8个转运商全部转运，最大转运量为4.8万m3；其余各周对6个转运商（转运商平均值）进行转运。设αi是每个供应商的订购量，v是每周购买成本，xn是某类供应商的数量，yn是某类供应商的原料价格，得到第1周目标函数及约束条件：

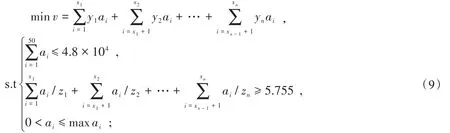
第2～24周与第1周目标函数相同，但约束条件不同，即

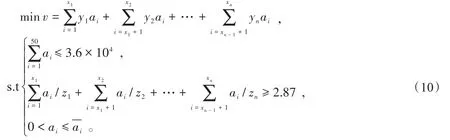
1.2.2 一般线性规划模型的求解结论

由以上两个线性规划模型得出未来24周的订购计划如表4所示。企业第1周向S126、S151和S374这3家供应商订货，材料均为C类，订购量分别为3 050 m3、21 260 m3和23 690 m3；第2～24周向28家供应商订购原材料，材料为A、C两类。综上可知，24周共需31家供应商。

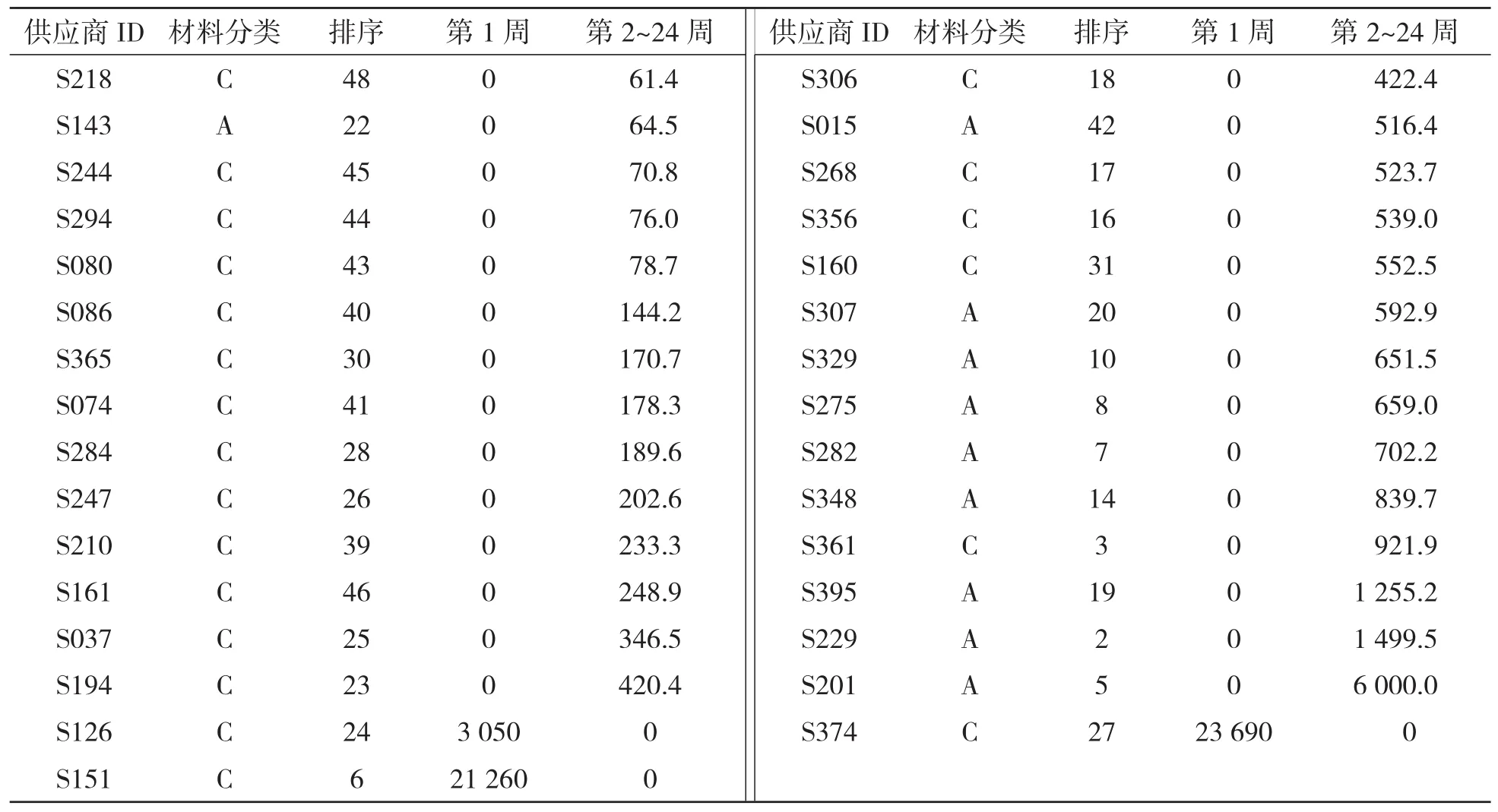
表4 正常生产未来24周原材料最佳经济订购方案

1.2.3 多维度线性规划模型的建立与求解

根据原材料类别，建立3类最低损耗量表，具体样式以表5为例。Ti是第i个转运商，i代表转运商总数；SAj表示某类第j个供应商，j表示A类供应商总数。αij表示第i个转运商对这类第j个供应商提供原材料的转运量。

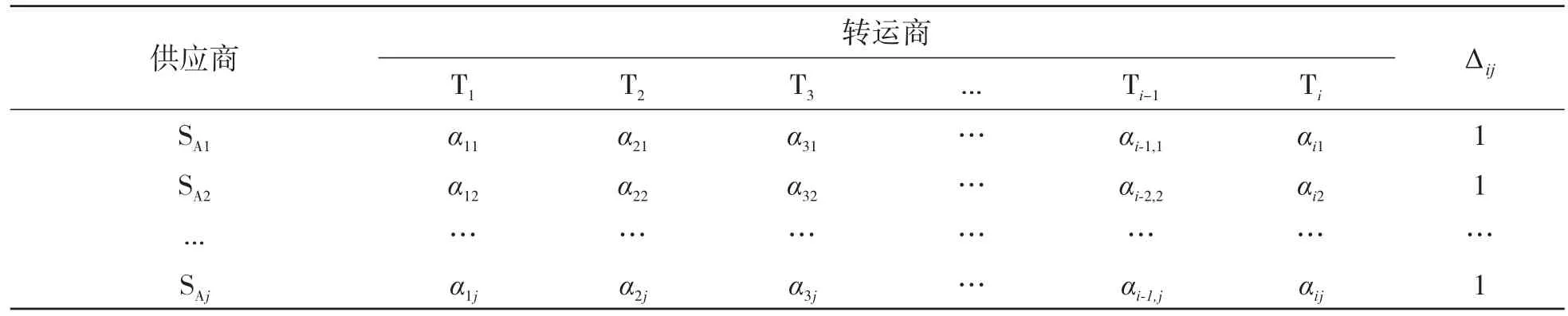
表5 A类转运方案结构表

因为一个供应商只能有一个转运商，所以得出约束条件：

每周最低损耗量的多维线性规划模型为：设第i个转运商对第一类第j个供应商提供原材料的转运量为αij，对第二类为βij，对第n类为σij，m为一运输过程中的最大量，τ是每周产能，μ是平均损耗量。

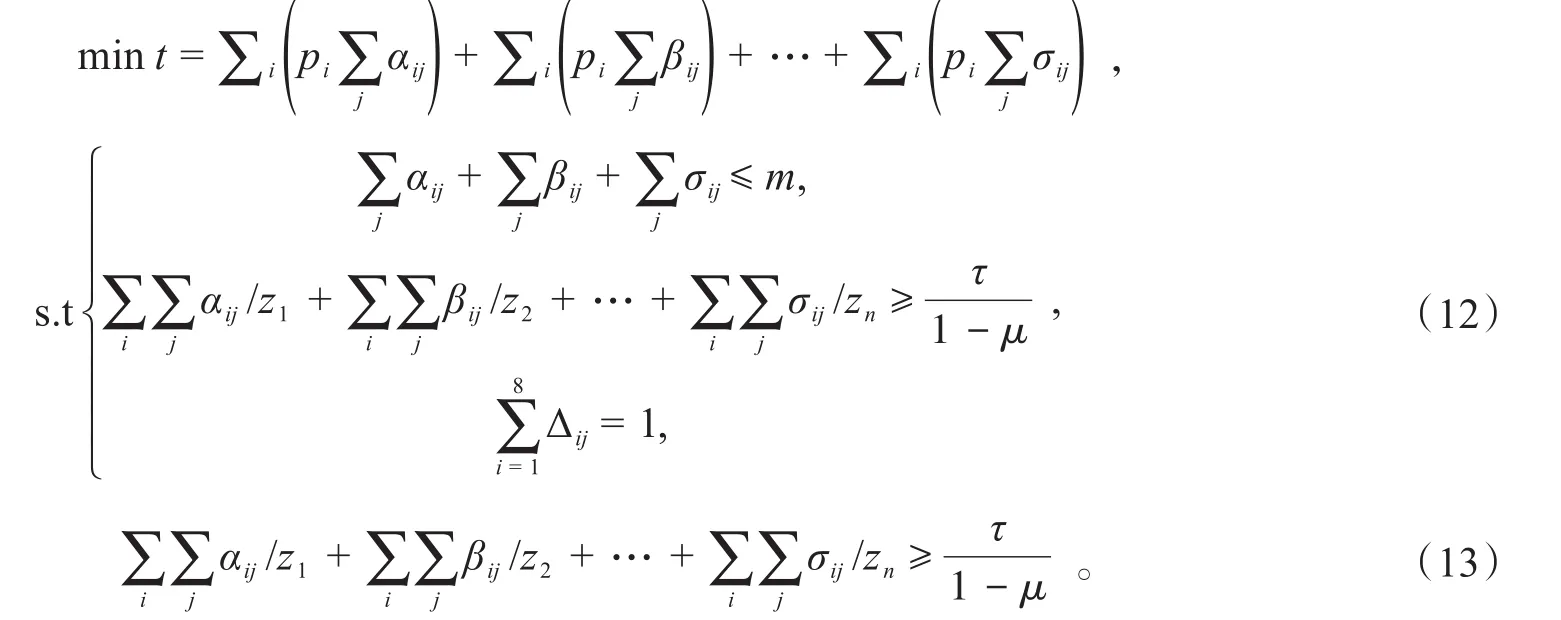
由订购方案可得第1周有3家C类供应商，第2～24周供应商A类10家、B类0家、C类18家。T1～T8每家转运商平均损耗率ρi分别为 0.019 0、0.009 2、0.000 9、0.015 7、0.028 9、0.005 4、0.020 8、0.010 1。

每周最低损耗量的多维线性规划模型及第1周最低损耗量的多维线性规划模型［4］如下：

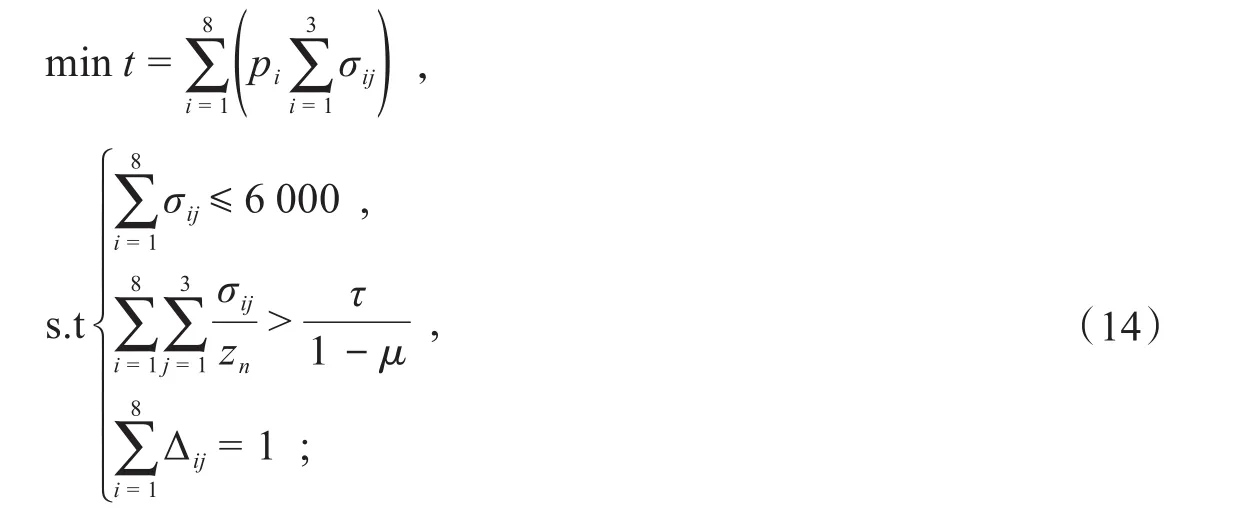
第2～24周每周最低损耗量的多维线性规划模型如下：

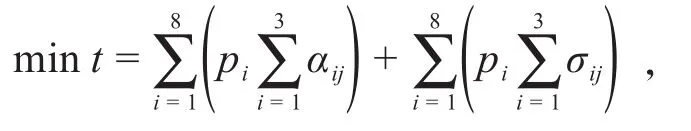
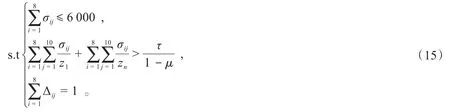
将每周最低损耗量分为第1周和第2～24周两类。第1周派8家转运商即全体转运商工作，损耗率为定值；第2～24周每周派6家转运商，因为不同转运商损耗率ρi不同，存在损耗率最低的约束条件。为使转运情况符合实际，基于MATLAB软件，参照每个转运商的转运概率，模拟转运商8选6进行随机转运。

根据已知数据发现240周订购量遵循6周一循坏的规律，因而转运方案也6周一循环，第1周属于特殊情况，由第2～7周的循环得到第8～24周的数据。

1.2.4 多维度线性规划模型的求解结论

根据多维度线性回归模型得到未来24周的转运方案，由于在第2～7周后以6周为一个循坏，本文仅展现第1～7周转运方案和转运损耗情况，如表6和表7所示。第1周派8家转运商即全体转运商工作，每家转运6 000 m3原料，预计将损失660 m3原料。第2周派转运商1、2、3、6，总损失97.0 m3原料；第3周派转运商 2、3、4、6，总损失 96.2 m3原料；第 4 周派转运商 2、3、4、6，总损失 96.2 m3原料；第 5 周派转运商1、2、4、5、6，总损失 185.5 m3原料；第 6 周派转运商 1、2、5、6，总损失 207.6 m3原料；第 7 周派转运商 1、2、6、8，总损失151.9 m3原料。可以发现每家转运商都参与原料转运，但损耗率低的转运商转运量和次数都更多。

表6 正常生产第1周转运方案和各转运商平均损失率表

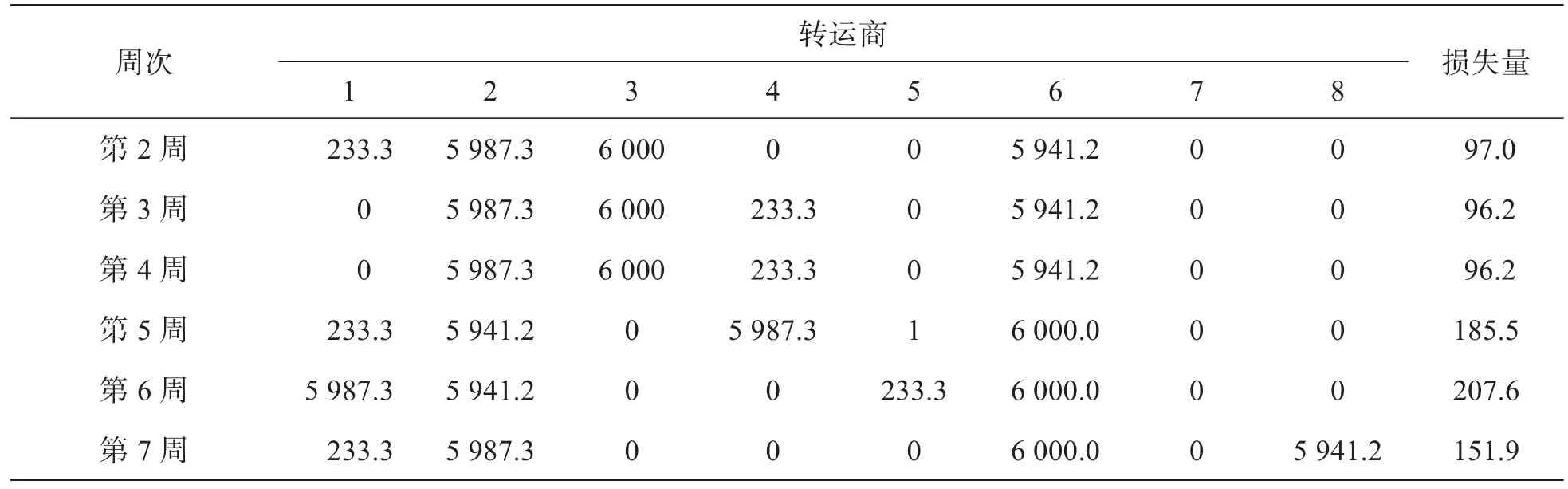
表7 正常生产第2～7周转运量和转运损失情况 单位：m3

1.3 压缩生产的模型建立与求解

1.3.1 多目标线性规划模型的建立与求解

为了达到减少运输存储成本和降低转运损耗率的目标，影响手段为增加A类订购量和减少C类订购量。将转运损耗率分为ρA、ρB和ρC，转运总量分为ζA、ζB和ζC。在已知条件中无目标重要性的特殊规定，默认成本和损耗率权重均为50%。第1周两大目标实现的多目标线性规划模型如下：

其中，Ψ是两大目标总和，λ是转运损耗量，ζi是每个供应商给予转运商的转运量，v是企业每周的购买成本。

第2～24周目标函数与第1周相同，但约束条件不同，即

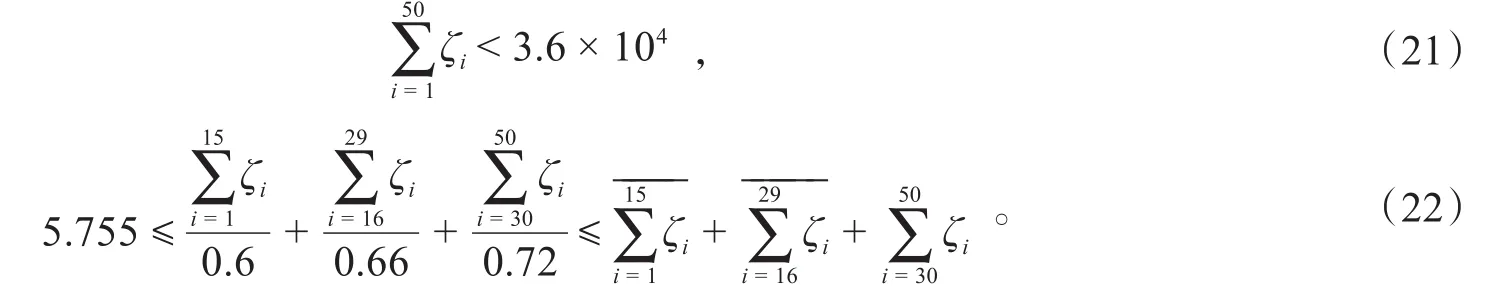
1.3.2 多目标线性规划模型的求解结论

基于多目标线性规划模型，得到在减少运输存储成本和降低转运损耗率两个目标下未来24周的订购计划。企业未来第1周仅需向3家供应商订购，分别为S126、S151和S374，材料均为C类，具体订购量分别为3 050 m3、21 260 m3和23 690 m3。企业未来第2～24周向33家供应商订购，材料仅有A、C两类，A类15家，C类18家。根据多目标线性回归模型的未来24周转运方案，第2～7周后以6周为一个循坏，主要展现第1～7周转运方案。

1.3.3 正常生产和压缩生产两种情况下订购和转运方案的实施效果

将给定条件中240周分成10份，每份24周记半年。统计得到每半年订货总体积、订货总产能、进价总花费、总损耗量，将正常生产时的订购转运方案与压缩生产规模后的订购转运方案进行对比，如表8所示。

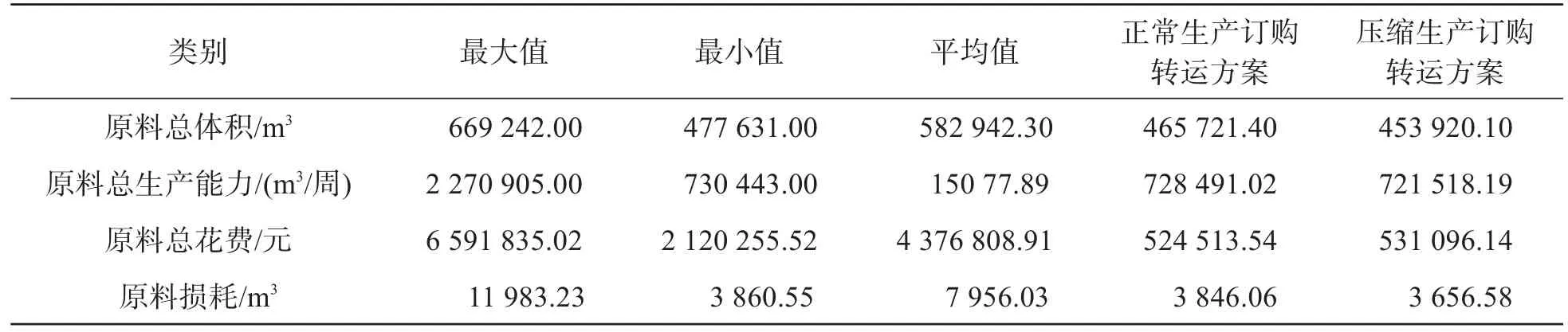
表8 正常生产和压缩生产订购转运方案中各类数据对比

在正常生产情形下，订购转运方案订购原材料得465 721.4 m3原料，较小于半年最小值477 631 m3，保证在生产前提下企业花费的存储费用最小，满足了每周生产2.82×104m3的基本要求和剩余两周生产需求的原材料库存量。本方案挑选的前31家供应商各个能力指标较强，所以按本方案订购原材料，供货量约等于订货量，稳定了日常生产；并且应急供应商供货天数基本大于100天且总供货量与最大供货量大于一般供应商，所以应急供应商有23周的时间准备供应；同时通过模拟实际得出转运方案的原料损耗量低于前5年的平均损耗量。

在压缩生产规模情形下订购转运的订购转运方案订购原材料，得到453 920.1 m3原料，略大于正常生产的465 721.4 m3，因为C类原料单位消耗体积小于A类原料，所以减少C类原料，总体积会变大；在保证生产的前提下使得花费的存储费用最小，满足每周生产的基本要求和剩余两周生产需求的原材料库存量。本方案选择了37家供应商，大于上一方案中的31家供应商，证明上一方案最少供应商是合理的；同时也继承了上一方案应对突发状况的做法和规定，最后用于原料的花费依旧低于前5年的平均值。

2 结语

本文从生产成本、收益和稳定性出发，设计出一套基于存在应急情况的多个供应商理想订购转运方案。基于熵权法的TOPSIS模型可以对各个指标进行权重的赋值，客观地反映供应商的重要程度。通过概率模拟构建的转运方案模型更贴合实际，对于该类型问题的求解及解决实际生活中的许多问题具有一定的借鉴意义。