巧动手，助解题——浅谈六年级数学解题技巧

文/中山市小榄镇绩东二小学 冯蔼玲

在教学六年级数学时，笔者发现讲过的题目还是有很多学生不会。即使有些题反复讲了几次，还是有学生不会解答。所以解题时，学生从何处入手，如何解题显得格外重要。通过实践，笔者认为进行有效的“动手”，对解题有很大的帮助。

一、巧动手之圈关键词

在解题时，有些关键词能够给我们解题方向。

例1：一个圆柱形粮囤，从里面量得底面半径是1.5米，高2米。如果每立方米玉米约重750千克，这个粮囤能装多少吨玉米？

此题，“立方米”三字告诉我们解题方向。立方米是体积单位，想到此题和体积有关。所以要求能装多少玉米，必须先求出粮囤的体积。此时提醒学生圈出“立方米”关键词，并注明“体积”二字。

关键词除了能告诉我们解题方向，还能帮助我们准确解题。例1中“圆柱”“半径”“千克”和“吨”等关键字词，保证了解题的正确性。求体积时，“圆柱”要和“圆锥”区分；而“半径”要和“直径”、“周长”相比较，很多题目会在这三个条件中随机切换；最后还要注意条件中单位“千克”和问题“吨”不同，所以还要进行单位转化。因此，解题时学生圈出“圆柱”、“半径”“千克”和“吨”等关键词，解题时就能够引起学生注意并提高正确率。

圈关键词这个方法，很多题目都适用。例如：表示数量关系的“一共”、“少”、“倍”；图形与几何中的“长方体”、“正方体”“圆锥”；行程问题的“相向而行”、“相背而行”等。找到对应关键词，相当于找到了它们隐藏的特征，能有效帮助学生解题。

二、巧动手之补充隐含条件

有时，学生动笔找出关键词，也找不到解题方向，怎么办呢？可以试试这个方法：补充隐藏条件，还原题目庐山真面目。

例2：一件衣服原价100，现价80，降价百分之几？

这道题求的是百分之几，就是求分率。求分率有两种题型：“求一个数是另一个数的百分之几”、“求一个数比另一个数多（少）百分之几”。例2属于哪种题型呢？第一眼看不出来。我们可以动动笔，还原题目的庐山真面目。关键词“降价”改为易懂的“少”，也就是少百分之几。条件中知道现价比原价少，所以补充隐藏条件后，改为“一件衣服原价100，现价80，现价比原价少百分之几？”隐含的条件对题目有了更充分的补充，使条件和问题更清晰。学生马上就能想到数量关系式：（大数-小数）÷单位“1”，找到解题的方向，打开学生的思路，帮助学生更快更准确解题。

三、巧动手之写数量关系

而单纯的写出数量关系式，在解决分数或者百分数题目时尤为适用。

学生通过分析，可知单位“1”是鸡的孵化期。将题目改为：鸭的孵化期是鸡的（1+），可以写出数量关系：鸡的孵化×（1+）=鸭的孵化期，代入数据即可求出鸭的孵化期。

补充隐藏条件，写出数量关系式在分数应用题中尤为适用。例如补充“单位1”，补充“成活率”，和扇形统计图结合在一起的百分数解决问题等等。补充完整题意后，写出数量关系式，问题就迎刃而解了。

四、巧动手之画图分析

如果题目条件较多，理不清数量关系；或者条件较相似，找出关键词后还找不到解题思路，这时可以试试画图分析。

例4：一装有水的圆柱形容器，底面直径10厘米，高12厘米。一不规则石块浸没在水中后，水面上升3厘米。求石块的体积。

这道题圈出关键词“圆柱”、“直径”、“上升”、“体积”后，虽然明白是求石块的体积，可是这不规则的石块又和圆柱有什么关系呢？我们可以通过画图分析题目。

通过画图（图1）可以知道，原圆柱形容器的水是图形黄色部分。加入石块后，水面升高了3厘米，也就是图形红色部分。所以要求石块的体积，就是求图中红色部分小圆柱的体积。也就是求已知直径10厘米，高3厘米的圆柱体积。

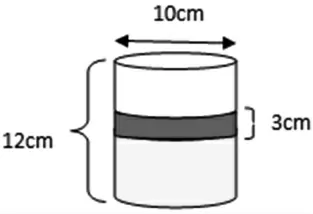
图1

根据题目，巧妙动笔动手，在圈画、剪拼的过程中，打开思维，找到解题方向和思路，都能够有效帮助大家解题，提高做题的正确率。