UN-U3Si2复合燃料的多尺度蠕变行为研究

杨青峰谢哲骁陈 平张 静高士鑫丁国琛周 毅尹春雨丁淑蓉何 梁孙 丹

1（中国核动力研究设计院核反应堆系统设计技术重点实验室 成都 610213）

2（复旦大学航空航天系力学与工程仿真研究所 上海 200433）

自福岛发生核事故以来，开发具有更高安全性的燃料一直是核领域关注的焦点。耐事故燃料应能提升反应堆在严重事故工况下的安全性，同时也能保持甚至提升正常运行状态下的性能［1−2］。与传统的UO2燃料相比，UN、U3Si2等燃料不仅具有更高的铀密度和更高的热导率，且其热导率随着温度的升高而增加［3−4］。UN、U3Si2燃料的高导热性能不仅保障了燃料棒在正常运行时具有较低的热储能，而且在事故工况下可以较快地导出衰变热；高铀密度则提高了中子经济性，可全面提高反应堆的运行利润［5−8］。因此，UN、U3Si2高铀密度燃料及其复合燃料是极具研发潜力的耐事故燃料。

UN-U3Si2复合燃料芯块在服役过程中会产生复杂的辐照-热-力耦合行为，其宏观蠕变性能直接影响其安全性。燃料的蠕变会引起应力松弛效应，影响复合燃料芯块内部的力学场及芯块与包壳之间的力学相互作用［9−10］。在不同的应力和辐照条件下，UN-U3Si2复合燃料的宏观蠕变应变及其内部主导的蠕变机制将会产生变化，与UN和U3Si2多晶燃料的蠕变性能密切相关。因此，对复合燃料的多尺度蠕变行为进行研究非常重要，可以为复合燃料芯块的优化设计及性能分析奠定基础。

已有的燃料蠕变性能研究主要针对UO2燃料展开，关于UN、U3Si2高铀密度燃料蠕变的理论及实验研究较少，关于UN-U3Si2复合燃料的蠕变模型研究尚未见报道。Zeisser等［11］对UN燃料进行了辐照条件下的单轴压缩蠕变试验，获得了温度520~1 050℃、应力5~63 MPa范围内的实验结果，但未进一步建立蠕变率模型。Hayes等［12］通过对UN高温压缩蠕变实验数据进行拟合，得到了UN蠕变率模型，此模型已被应用于爱达荷国家工程和环境实验室开展的UN燃料堆内热-力学行为的计算模拟。此外，Brucklacher等［13］也针对UN燃料开展了蠕变实验研究，得到了不同条件下的实验数据，但未进一步发展蠕变率模型。Mercado［14］对U3Si2进行了高温下的单轴压缩蠕变试验，获得了温度范围为850～1 050℃，应力范围为30～80 MPa下的实验数据，并拟合得到了与温度、应力相关的蠕变率模型；Freeman［15］也利用Mercado得到的实验数据，采用另外的函数形式得到了新的蠕变率模型；Yingling等［16］进一步考虑了晶粒尺寸的影响，得到了与温度、应力和晶粒尺寸关联的蠕变率模型，并引入U3Si2-SiC燃料堆内热-力学行为的数值模拟研究。Metzger［17］基于已有的蠕变变形主导机制的分析，提出了U3Si2的蠕变率模型，尚未得到实验的验证。目前的这些蠕变率模型是经验公式，没有综合考虑辐照蠕变及热蠕变的贡献，也没有全面考虑不同应力及温度条件下的蠕变机制进行建模，因此需要结合已有报道的所有实验结果建立新的蠕变率模型。

利用文献中已有的蠕变实验数据，基于不同条件下的主控蠕变机制建立了UN和U3Si2的蠕变率模型，并基于均匀化理论获得UN-U3Si2复合燃料的宏观等效蠕变应变与各组分贡献的关联模型。建立了组分随机分布的有限元模型，计算模拟了UN-U3Si2复合燃料辐照条件下的拉伸蠕变实验，获得了各组分对宏观蠕变应变的定量贡献及主控的蠕变机制，并考察了燃料辐照肿胀对复合燃料多尺度蠕变行为的影响。

1 UN和U3Si2燃料的辐照热-力学性能模型

UN-U3Si2复合燃料由UN和U3Si2组成，本节给出其弹性性能和辐照肿胀模型。

1.1 弹性常数

UN的弹性模量（EUN）和泊松比（νUN）分别为［12］：

式中：ρ是理论密度比，%，本文取100；T是温度，K。

U3Si2的弹性模量（EU3Si2）和泊松比（νU3Si2）分别为120 GPa和0.177［14］。

1.2 辐照肿胀模型

UN和U3Si2的辐照体积肿胀采用如下经验模型描述［18−19］：

式中：Bu表示燃耗，单位为FIMA（Fissions Per Initial Heavy Metal Atoms）。

2 复合燃料的多尺度蠕变模型

2.1 多晶材料相的蠕变率模型

由于目前缺乏完善的UN和U3Si2蠕变率模型，本研究结合文献报道的实验结果，综合考虑辐照蠕变和热蠕变的贡献，并基于不同应力及辐照工况条件下的蠕变机制分析，建立两种组分材料的新蠕变率模型。

UN和U3Si2均为多晶材料，多晶材料的蠕变变形主要有以下几种典型机制［20］：空位扩散机制［21］、位错攀移辅助滑移机制［22］、位错湮灭机制［23］。这些机制与晶粒内部各类缺陷的运动以及晶粒之间的相互作用有关，在不同条件下的主导蠕变机制不同，也因材料而异。

对于UN材料，根据实验结果［11−12］获知，在中低温下空位扩散蠕变机制主控；在低温下主要发生辐照蠕变，在中等温度下辐照蠕变和热扩散蠕变均有贡献；在高温下以位错蠕变机制为主，不受裂变率的影响。通过蠕变率与应力之间的关系可以判断，高温蠕变主要由位错湮灭机制所导致。空位扩散机制下，蠕变率与应力成正比关系，与晶粒尺寸的平方成反比关系；位错湮灭机制下，蠕变率与应力的4.5次方成正比关系，与晶粒尺寸无关。基于这两种蠕变机制的典型特征，结合实验结果建立如下等效蠕变率模型：

式中：ε̇cr是宏观蠕变 率，s−1；ḟ是裂变率，fissions·(cm3·s)−1；R是理想气体常数，取8.314 J·(mol·K)−1；σ是应力，MPa；d是晶粒尺寸，μm；A1=6.592 6×10−23，A2=1.613 8×10−2，QA=114 007 J·mol−1，B1=2.285 6×10−3，QB=329 040 J·mol−1。

对于U3Si2材料，根据实验结果［16］分析得出，其蠕变变形由空位扩散机制和位错攀移辅助滑移机制共同作用，且在低温下主要来自于辐照蠕变。对于这种燃料，其空位热扩散蠕变和位错攀移辅助滑移蠕变两部分均受裂变率和温度的影响［24］。目前缺乏U3Si2燃料的辐照蠕变实验数据，根据文献［17］得出，特定裂变率下的辐照蠕变率可由转变温度下的热蠕变推导得到。空位扩散机制下，蠕变率与应力成正比关系，与晶粒尺寸的平方成反比关系；位错攀移辅助滑移机制下，蠕变率与应力的3次方成正比关系，与晶粒尺寸无关。所以，结合实验结果得到了如下的等效蠕变率模型：

式中：A1=6.524 8×10−23，A2=4.792，QA=172 647 J·mol−1，B1=3.361 6×10−29，B2=3.578 6×10−6，QB=171 453 J·mol−1。

式（5）和式（6）中的各系数均通过文献中的蠕变实验数据［11−12，16］及反推的辐照蠕变数据拟合得到，为解决多参数拟合的问题，针对低温和中高温区采用了分批次拟合的方法。在低温下，温度相关项的量级远小于辐照相关项，所以先拟合出与温度无关的辐照主导项的系数，再利用中高温下的实验数据，将总蠕变率减去辐照相关项的贡献后，得到热蠕变率，进一步拟合得到温度相关项的系数。

图1（a）、（b）分别展示了采用式（5）和式（6）计算得到的UN和U3Si2蠕变率，并同时给出了文献上的实验结果［11−12，16］。其中的实验结果包含了辐照条件下的数据及堆外蠕变实验结果，也具有不同晶粒尺寸的核燃料试样的蠕变实验结果。可以看出，模型计算结果与实验结果吻合较好，证明了所建立模型的合理有效性。

图1 UN蠕变(a)和U3Si2蠕变(b)模型计算值与实验值的对比情况（彩色见网络版）Fig.1 Comparison of the calculated and experimental values of the UN creep model(a)and the U3Si2 creep model(b)(color online)

2.2 复合燃料的宏观等效蠕变模型

在宏观外载作用下，UN-U3Si2复合燃料试样的宏观蠕变变形来自于UN和U3Si2的蠕变贡献。可以基于均匀化理论［25−27］，通过选取代表性体元模拟单轴拉伸蠕变实验，通过对细观非均匀分布的蠕变应变进行体积平均，计算得到复合燃料的宏观等效蠕变应变，并同时获得UN和U3Si2两相对复合燃料宏观蠕变的定量贡献及主控蠕变机制。

对于计算模拟中的每个增量步，以增量步起始时刻的构形作为参考构形，各应变增量满足：

式中：Δεij为复合燃料芯块的总应变增量；(Δεij)f和(Δεij)m分别为弥散相U3Si2和基体相UN对各自体积所平均得到的总应变增量；fν和fm分别为弥散相和基体相的现时体积分数。

由于蠕变应变为偏斜张量，而辐照肿胀应变为球形张量，则复合燃料的宏观体积变化主要来自各组分材料辐照肿胀的贡献。由于弹性应变的贡献可以忽略，可得复合燃料拉伸方向（x方向）的宏观等效蠕变应变增量满足：

3 复合燃料单轴拉伸蠕变实验模拟的有限元模型

基于§1中的UN和U3Si2燃料弹性模型和辐照肿胀模型，以及§2.1中建立的UN和U3Si2多晶燃料蠕变率模型，建立了旋转坐标系下的三维大变形增量本构关系，推导了应力更新算法和一致刚度模量，并编写了UMAT子程序，在ABAQUS有限元计算平台实现了UN-U3Si2复合燃料的单轴拉伸蠕变实验的有限元模拟。

目前，UN-U3Si2复合燃料芯块主要是U3Si2和UN粉末共同烧结制备而成［28］，芯块的金相结构剖面如图2所示［28］。UN-U3Si2复合燃料可以视作以U3Si2为弥散相、以UN为基体相的弥散型核燃料，在结构上类似颗粒复合燃料，但U3Si2颗粒的形状不规则、大小不均匀，在UN基体中也呈现非均匀分布。

图2 UN-U3Si2复合燃料芯块组织Fig.2 Microstructure of UN-U3Si2 composite fuel pellets

根据复合燃料的微观结构特征和两相分布情况，暂不考虑孔隙的存在，本文针对立方体形代表性体元发展了如下的随机建模方法：

1）将整个立方体体元划分均匀的六面体网格；

2）在计算前，借助外部程序进行随机建模，获得两相材料的空间分布情况，并输出文本文档；

3）在计算开始时刻，通过UMAT读取上述文本文档和单元积分点坐标，根据积分点坐标判断材料属性，并记录材料状态变量；

4）在每一个增量步开始时，读取最初记录的材料状态变量，并调用对应的材料子程序。

图3展示了通过外部程序进行随机分布建模的流程示意图。20%弥散相含量的复合燃料随机分布有限元模型如图4所示。

图3 弥散相随机分布建模的流程示意图Fig.3 Flowchart diagram of random distribution modeling

图4 随机分布模型示意图Fig.4 Schematic diagram of random distribution model

根据细观力学的思想，复合燃料在宏观上由代表性体元周期性排列得到。在宏观外载作用下，代表性体元的变形亦周期性分布［27］。对于内部弥散相随机分布的代表性体元，由于其没有几何上的对称性，所以需要施加位移约束使其满足边界条件的周期性。周期性位移边界条件可表示为［29］：

其中：如图5所示，N0和Nj（j=1，2，3）是4个主节点和是相对面上的对应点，正负号代表相应点所在面的外法线方向沿坐标轴的正向或负向。uj+、uj−、Uj、U0分别是对应点和主节点的位移。将主节点N0设置为固定，约束主节点Nj在其他两个方向上的位移，用于约束刚体平动和转动。以x方向为拉伸方向，体元在法线为x方向的两个面上分别施加大小为P的均布拉力。需要指出，由于需要同时满足位移周期性条件，虽然在周期性边界上施加了均匀拉力，周期性边界上的实际应力非均匀分布且满足应力的周期性。

图5 代表性体元的周期性边界条件及施加载荷示意图Fig.5 Schematic diagram of periodic boundary conditions and applied loads for cube-shaped voxels

4 结果与讨论

4.1 辐照肿胀对复合燃料多尺度蠕变行为的影响

本文模拟复合燃料辐照条件下的单轴拉伸蠕变实验，考虑了两种材料的辐照肿胀贡献，以更好地模拟复合燃料的辐照效应。虽然在计算宏观等效蠕变应变时，已经去除了辐照肿胀所引起的体积应变贡献，但是各组分材料的辐照肿胀会影响复合燃料细观的应力状态，进而影响多尺度的蠕变变形。为了研究辐照肿胀对复合燃料多尺度蠕变行为的影响，本文也对不考虑组分材料辐照肿胀的算例进行了计算模拟，获得了在均布拉力50 MPa、温度500 K、裂变率1020fissions·m−3·s−1条件下的结果。

图6给出了考虑与不考虑辐照肿胀两种情况下的宏观等效蠕变应变随时间的演化结果。可以看到，考虑辐照肿胀情况下的结果略大于不考虑辐照肿胀下的结果，其相对偏差随着燃耗的增长而逐渐增大。在裂变密度达到4.32×1027fissions·m−3时，考虑辐照肿胀计算得到的等效蠕变应变为0.037 78，不考虑辐照肿胀计算得到的等效蠕变应变为0.035 772，偏差为5.2%，总体上差别不大。

图6 考虑与不考虑辐照肿胀情况下宏观等效蠕变应变的对比Fig.6 Comparison of macroscopic equivalent creep strain with and without irradiation swelling

图7（a）和（b）分别给出了考虑与不考虑辐照肿胀计算得到的细观von Mises等效应力分布图，为复合燃料在裂变密度达到4.32×1027fissions·m−3时的结果。可以看到，对于考虑辐照肿胀的情况，由于弥散相和基体相均会产生肿胀，且体积肿胀不一致，导致两相的界面处发生强烈的力学相互作用，最大的von Mises应力近300 MPa，大约为施加的外部均布拉力的6倍；最小的von Mises应力约为30 MPa，低于外部施加的均布拉力。对于不考虑辐照肿胀的情况，两相的von Mises应力基本呈均匀分布，大小接近于施加的外部均布拉力。

图7 裂变密度达到4.32×1027 fissions·m−3时的von Mises应力云图（剖面图）(a)考虑辐照肿胀，(b)不考虑辐照肿胀Fig.7 Von Mises stress contourplots(section view)at the fission density of 4.32×1027 fissions·m−3(a)With radiation swelling,(b)Without radiation swelling

图8分别针对考虑与不考虑辐照肿胀两种情况，给出了裂变密度达到4.32×1027fissions·m−3时的细观等效蠕变分布云图。可以看到，对于考虑辐照肿胀的情况，非均匀分布的von Mises等效应力导致了等效蠕变的非均匀分布，等效蠕变应变的最大值约为最小值的3.2倍。对于不考虑辐照的情况，等效蠕变应变虽然也非均匀，但最大和最小值相差不大。

图8 裂变密度达到4.32×1027 fissions·m−3时的等效蠕变云图（剖面图）(a)考虑辐照肿胀，(b)不考虑辐照肿胀Fig.8 Equivalent creep contour plots(section view)at the fission density of 4.32×1027 fissions·m−3(a)With radiation swelling,(b)Without radiation swelling

结合以上结果可知，由于两相材料的辐照肿胀不同，两相材料之间需要变形协调，导致两相之间存在较为强烈的力学相互作用。但由于离开界面处的基体应力及颗粒相的应力被削弱了，所以两相材料的辐照肿胀对复合燃料宏观等效蠕变的影响可以忽略。

4.2 复合燃料宏观蠕变应变的细观主导机制分析

通过均匀化方法，可以得到弥散相和基体相对总蠕变应变的贡献，也可以得到不同机制蠕变的占比情况，分别如图9、10所示。可见，基体相对总蠕变的贡献较大。裂变密度达到4.32×1027fissions·m−3时，基体蠕变在总蠕变中的占比约为79%，这主要由于基体相在复合燃料的体积分数较大。由图10可以看出，辐照扩散蠕变占主导，其占比随时间逐渐减小；辐照位错蠕变也产生了可观的贡献，其占比随时间逐渐增大，这主要是由于组分材料的辐照肿胀使得复合燃料内部产生了越来越强烈的力学相互作用；热扩散蠕变和热位错蠕变基本没有贡献。本研究所考虑的温度较低，热蠕变基本可以忽略，所以在本文的条件下辐照蠕变机制占主导。

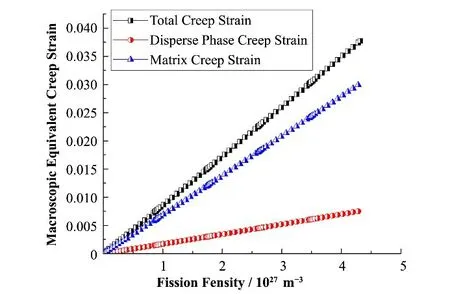
图9 弥散相和基体相对总蠕变应变的贡献Fig.9 Contribution of dispersed phase and matrix to total creep strain

图10 各蠕变贡献的占比Fig.10 Proportions of different creep contribution

5 结语

本文基于已有文献中的蠕变实验结果，综合考虑了辐照蠕变及热蠕变的贡献，通过分析各种条件下的主导蠕变机制建立了UN和U3Si2多晶燃料的蠕变率模型，证明了模型的合理有效性；同时利用均匀化理论建立了UN-U3Si2复合燃料宏观等效蠕变和两相贡献的关联模型；并发展了随机建模方法，实现了UN-U3Si2复合燃料辐照条件下的单轴拉伸蠕变实验的有限元模拟，获得两相材料在复合燃料宏观蠕变中的定量贡献，并分析了主控的蠕变机制。同时，考察了组分材料的辐照肿胀对复合燃料多尺度蠕变行为的影响，得到的主要结论如下：

1）考虑和不考虑辐照肿胀的计算结果表明：由于组分材料的辐照肿胀行为的差异性，导致复合燃料的颗粒和基体相产生了强烈的力学相互作用，在裂变密度达到4.32×1027fissions·m−3时的最大von Mises应力约为外部均布拉力的6倍；由于同时存在细观应力被削弱的区域，组分材料不同的辐照肿胀对宏观等效蠕变应变的影响很小，可以忽略。

2）在均布拉力50 MPa、温度500 K、裂变率1020fissions·m−3·s−1的条件下，基体相对总蠕变的贡献较大，在裂变密度达到4.32×1027fissions·m−3时，拉伸方向的基体蠕变在总蠕变中的占比约79%；在此参数范围内，辐照扩散机制蠕变占主导，其占比随燃耗的增长逐渐减小；而辐照位错蠕变的占比随燃耗的增长逐渐增大，归功于组分辐照肿胀对细观应力场的影响；热扩散机制蠕变和热位错机制蠕变基本没有贡献。

作者贡献声明杨青峰：论文整体设计，起草文章；谢哲骁：起草文章，模型计算；陈平：对文章作批评性审阅，研究经费支持；张静：模型计算指导；高士鑫：对文章作批评性审阅；丁国琛：模型计算指导；周毅：论文整体设计；尹春雨：论文整体设计；丁淑蓉：研究指导，论文修改；何梁：数据处理；孙丹：数据分析。