基于“大概念”的高三复习课探索——以“隐形圆问题”为例

冯宇斌 翟荣俊

(江苏省无锡市洛社高级中学 214187)

1 背景描述

单元教学是落实数学核心素养的有效途径．其中，“大概念”起到引领的作用．所谓“大概念”，是指能将众多数学知识联成一个整体的数学学习核心，它可以是一个具体的上位概念、重要命题或原理，也可以是一个数学主题、观点或思想方法．例如，平面向量是一类重要的数学对象，沟通了几何与代数，是解决问题的有力工具，可以视作知识型大概念；换元法是代数变形的常用方法，起到简化结构、突出实质的作用，在函数、数列、不等式中都有体现，可以视作方法型大概念；转化与化归是数学解题的依据和导向，同时也是重要的数学思想方法，可以视作思想型大概念．

图3

点评具体破解时，可以从“数”的性质角度，通过坐标法来分析；或从“形”的特征角度，通过几何法来处理．

高三数学试卷讲评课，要依据高考复习背景与试卷讲评的课型特征和学生实际，选择恰当的教学策略，提升数学关键能力，优化应试策略，为情境而教、为素养而教．

2 教学设计

例1已知Rt△ABC的斜边为AB，且A(-1,0)，B(3,0)．

(1)直角顶点C的轨迹方程为；

(2)直角边BC的中点M的轨迹方程为．

解(1)设AB中点为D(1,0)，则CD=2，故C的轨迹是以D为圆心、2为半径的圆(不含A,B)，方程为(x-1)2+y2=4(y≠0)．

(2)设DB中点为N(2,0)，则MN=1，故M的轨迹是以N为圆心、1为半径的圆(不含D,B)，方程为(x-2)2+y2=1(y≠0)．

(也可以设M(x,y)，则C(2x-3,2y)，代入(1)中的方程，同样得出结果，注意不含D,B)

小结 ①定点(圆心)和定长(半径)是确定圆的两个几何要素；②根据具体问题，舍去一些不符合条件的点．

变式 (多选题)已知圆C的方程为x2+y2-4x=0．若直线y=k(x+1)上存在一点P，使过点P所作的圆的两条切线相互垂直，则实数k的可能取值是( )．

A．1 B．2 C．3 D．4

设计意图学会通过几何分析，确定定点和定长找出隐形圆．同时注意“增点”问题，加深对曲线方程这一概念的理解．

思考 ①确定圆的几何要素，除了圆心和半径，还可以是什么？(CA⊥CB，或者说AB是圆的直径)

②已知A(x1,y1),B(x2,y2)是圆的一条直径的两个端点，求圆方程．

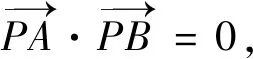
该方程称为圆的直径式方程，简称直径圆方程．

例2已知点A(-1,0)，B(1,0)均在圆C:(x-3)2+(y-4)2=r2外，且圆C上存在唯一一点P满足AP⊥BP，那么半径r的值为．

小结 垂直这一几何条件，往往隐含直径圆．

小结 本题从几何角度难以直接得出点P的轨迹，通过设点用代数方法求出P的方程．并且有如下结论：平面内到两个定点的距离之比是定值(不等于0,1)的点的轨迹是圆，称为阿波罗尼斯圆．

变式1 已知两定点A(-3,0)，B(1,0)， 若直线l:x+ay-2=0上一点M满足MA2+MB2=16，则实数a的取值范围是．

设计意图例3及其变式的处理方法都是设点、列式、化简，这是求轨迹方程的一般方法．同时学生意识到背景条件虽有变化，背后都是隐形圆，轨迹意识得到强化．

例4(拓展)已知圆O:x2+y2=1，C:(x+1)2+y2=9，直线l与圆O相切，与圆C相交于A,B两点，分别以点A,B为切点作圆C的切线l1,l2，设直线l1,l2的交点为P，则OP的最小值为．

设计意图例4及其变式可视作隐形圆问题的延伸．例4是综合问题，不仅要求学生具备较强的“动点找轨迹”意识，同时要熟悉基本模型；变式可以用常规解三角形的方法去做，较繁琐．抓住条件CA+CB=3c=12>AB，本质上是一个隐椭圆问题，从而建立坐标系巧妙求解．

课堂小结，如图1所示．

图1

3 教学反思

“大概念”组织高三复习课，更容易揭示知识间的联系，提高学生解决综合问题的能力．对于高一、高二的新授课，我们常提到单元教学、大概念……而对于高三复习，笔者认为更应当去强化、去落实．高三学生具备了相当多的知识，积累了一定的方法和经验，但缺乏整体性的认识，高三复习需要解决知识、方法的孤立问题．先确定大概念，再精心选择内容相近、方法类似、本质相同的问题，学生的数学视野一旦打开，能力、素养也会得到相应的发展．例如，以多变量问题作为大概念去组织素材，消元、固元、基本不等式、函数思想等都可以容纳进去．

“大概念”组织高三复习课，有助于解题方法的优化和取舍，提升思维的深刻性．一题多解是高三复习课常采用的方式，能够帮助学生打开思路．实际操作过程中，有一个问题常被忽视，就是如何引导学生对多种解法进行评价、选择、优化，甚至取舍．同时也并不是所有问题都应当或值得去追求多解的．用“大概念”的观点看待这个问题，就是要区分该方法是否是一般方法，其适用范围是否广泛．有了这样的认识，我们才可能做到善于选择，大胆舍弃，而不是刻意寻求多种解法，降低课堂效率的同时浪费宝贵的时间．

编者按为密切编辑部与中学的联系，本刊编委第28次“走进课堂”，于2022年9月15日赴江苏省句容高级中学观课议课．江苏省句容高级中学由句容文化名人丁宣孝先生创建于1926年，建校以来，虽历经风雨涤荡，几易校名，但终能弦歌不辍，薪火相续．近百年砥砺风雨，学校积淀了丰富而深厚的文化底蕴．学校秉承“诚·毅”校训，大力打造“诚毅果行，守正出新”的精神文化，形成了“爱国、守纪、勤奋、健美”的校风，“敬业、奉献、求实、创新”的教风和“奋发、探索、团结、进取”的学风．学校曾获“江苏省文明单位”“江苏省实施素质教育先进学校”等多项省部级集体荣誉．近几年来，承载着创建“高品质示范高中”的梦想，全校上下立足新起点，瞄准高目标，坚持“以人为本，立德为先，民主和谐，全面发展”的办学理念，着眼于校园文化建设，在努力使所有学生得到充分发展的同时，积极促进教师素质的全面提升，争取大幅度提高教育教学质量，以期使学校综合办学绩效获得社会的更广泛认可．