关于简支组合梁的应力研究与分析

张洪霞，邹雪

（攀枝花学院土木与建筑工程学院，攀枝花 617000）

组合梁通常是通过栓钉、预埋件和焊接等连接方式将两层及以上的单梁组合在一起，多由两种或两种以上的材料组成。在工程实际运用中，常采用螺栓固定的方式使得原本独立的构件形成一个整体。试验通过采用四根螺栓对称布置的方式将原本独立的两根或三根单梁固定成一个整体。通过反复的试验，观察不同层数和不同材料相组合的整梁在连续加载过程中构件纯弯曲段应变的变化规律，以及对于强度、刚度等方面发生的变化，结合理论分析对组合梁纯弯曲应力—应变规律进行一个分析归纳并总结。

1 理论分析

在纯弯曲条件下，将不同材料、尺寸一致的单梁经螺栓固定形成的双层矩形截面组合梁作为力学模型。其中，上部梁的弹性模量为E1、截面面积为A1；下部梁的弹性模量为E2、截面面积为A2，A1=A2。

考虑图1所示的组合梁，由四根螺栓紧密连接，假设两根梁之间相互接触密合且摩擦力可略去不计，则梁受力变形之后，两梁在相互接触面之间不可发生相对滑移，此时可将组合梁视作一个整体。

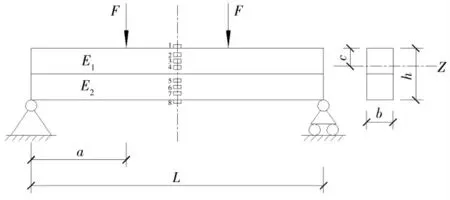
图1 双层组合梁力学模型简图Fig.1 Mechanical model of double-layer composite beam

1.1 几何、物理与静力学关系分析

1.1.1 几何关系

研究横截面梁不同位置的y与正应变的变化规律，根据平面假设变形，线应变[1-5]：

注：y表示测点离中性层的距离；ρ表示中性层的曲率半径。

1.1.2 物理关系

研究横截面梁不同位置的y与正应变的变化规律，不考虑梁纵向的相互挤压，则认为理想条件下截面各点都处单向受力状态，根据该状态下的胡克定律，正应力

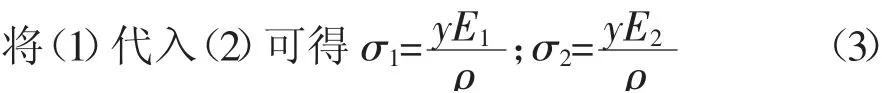
注：σ1，σ2为上下梁的正应力。

1.1.3 静力学关系

在纯弯情况下，横截面上的轴力FN=0，对y轴的力矩My=0

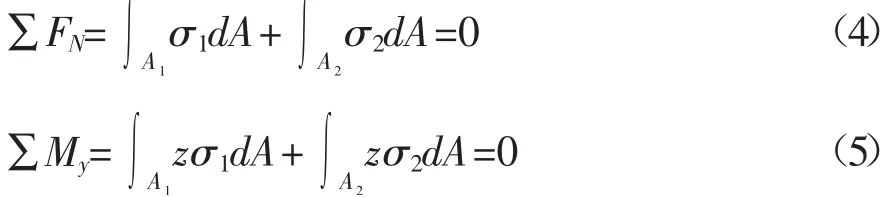
整个横截面内力系仅存在对z轴的力矩Mz：

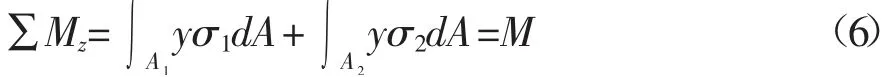
1.2 确定中性层的位置

同时令

即E1S1+E2S2=0（5）

注：S1、S2为截面部分面积A1、A2的静距。

设中性层离整梁上边缘的距离为C[6]，截面A1、A2的形心纵坐标分别为

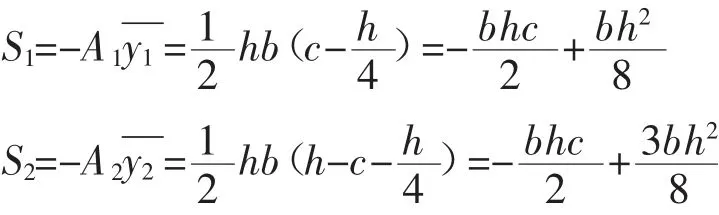
1.2.1 正应力推导

将（3）代入（6）

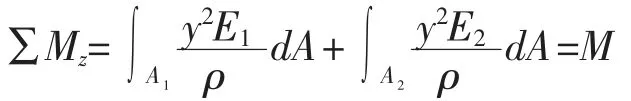
1.3 三层组合梁推论

同理可得，在三层矩形组合梁力学模型中（见图2所示），仅考虑纯弯曲情况下，整理得出三层矩形组合梁理论计算公式。其中，上、中、下梁弹性模量为E1、E2、E3；截面面积为A1、A2、A3，A1=A2=A3；整梁的长、宽、高分别为L、b、h。

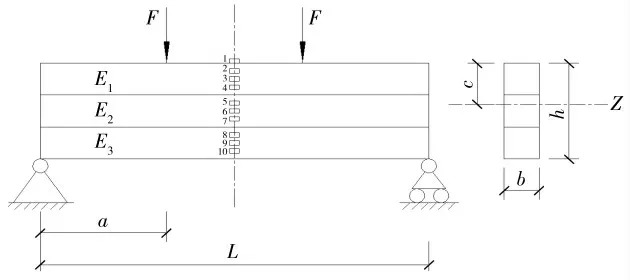
图2 三层组合梁力学模型简图Fig.2 Mechanical model of three-layer composite beam

1.3.1 中性层位置的确定

1.3.2正应力的公式

根据上述两层与三层组合梁在纯弯曲条件下，推导出了组合梁的中性层理想位置和正应力理论公式，为了运用于实际工程，理论结合实际，需要通过不同形式、材料的组合梁的内力分布测试实验来验证理论的准确性。

2 实验测试

实验利用电测技术[7-9]，在符合材料力学中试件承受纯弯曲变形的前提下，将硬铝和低碳钢两种材料进行不同组合方式的叠放，形成三层硬铝组合梁、三层铝-钢-铝组合梁、双层低碳钢组合梁以及双层硬铝组合梁，然后对梁上均匀分布的各点进行实测。以此验证实测数据是否符合理论上的应力-应变变化规律。

2.1 实验设备

包括程控静态应变仪、多功能力学实验台（见图3）、游标卡尺。

图3现场实测构件图Fig 3 Field measured component diagram

2.2 实验基本原理

实验试件单梁尺寸为440×36×18（mm），将试件在纯弯曲部分沿高度方向按h/4平行于中性层布置应变片，从上至下依次标记测点如图1和图2所示，应变片的电阻值为120 Ω，灵敏系数为2.08，在适当位置放上对应材料的温度补偿片[10-11]。然后使用程控静态应变仪，按惠斯登1/4桥路对选择点采用连续等间隔加载的方式（加载初始载荷以及加载间隔如表1所示）进行测量，得出实验数据。

表1初始载荷F及等间隔加载ΔF情况Table 1 Initial load F and equal interval loadΔF

试验的两种材料弹性模量分别为低碳钢210 GPa，硬铝70 GPa，由各测点处于单向应力状态下，由胡克定律可求得各测点实测应力值：Δσi=EΔεi（注：试验采用等间隔连续加载，平均应变差值计算实验应力。）

3 结果比较与分析

3.1 测点的应力值及误差

将理论公式推导计算得到的各测点理论应力值和根据胡克定律Δσi=EΔεi得出的各测点实验应力值以及根据相对误差公式求得的相对误差值列于表2～表5中，相对误差=（σ测-σ理）/σ理×100%。

表2双层低碳钢组合梁Table 2 Double-layer low carbon steel composite beam

表3 双层硬铝组合梁Table 3 Double-layer hard aluminum composite beam

表4 三层铝-钢—铝组合梁Table 4 Three-layer aluminum-steel-aluminum composite beam

表5 三层硬铝组合梁Table 5 Three-layer hard aluminum composite beam

3.2 测点的应力值分布图

将各种组合下的组合梁理论应力值和实验应力值分布及对比如图4~图7所示（其中横坐标代表各测点位置，纵坐标代表应力值）。

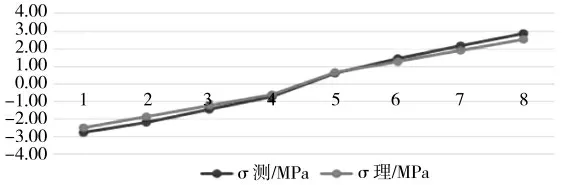
图4 双层低碳钢组合梁Fig.4 Double-layer low carbon steel composite beam

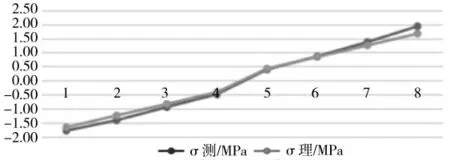
图5 双层硬铝组合梁Fig.5 Double-layer hard aluminum composite beam

图6 三层铝-钢-铝组合梁Fig.6 Three-layer aluminum-steel-aluminum composite beam

图7 三层硬铝组合梁Fig.7 Three-layer hard aluminum composite beam

从图及表中可以得出以下结论：

（1）由实验数据可知，不同材料、不同组合方式的等截面的组合梁应力分布都呈线性规律分布，分布规律与理论值正应力分布图基本吻合，且与单根梁分布规律类似。

（2）双层和三层的同种材料组合梁中应力值都成线性分布，螺栓固定处未发生应力跳跃，中性层大致沿截面高度方向对称，故可将螺栓固定的双层和三层组合梁看成一根整梁。在三层不同材料的钢铝钢组合梁中，螺栓固定处未发生应力跳跃，也是成线性分布，故选取合适的不同材料经螺栓固定可看作一根整梁。

4 结论

梁在工程中应用十分普遍，特别是对于一些大工程，常采用将其叠合后用螺栓对称固定的方式，而不同的叠合方式对梁的应力和抗裂性会有很大影响，所以在不同的叠合方式中应将弹性模量较小、峰值拉应变较大的材料放在下层以提高其抗裂性能[12]。由不同材料组合而成的梁，可以充分利用不同材料的性能，从而在强度、刚度、耐腐等方面具备单根梁无法比拟的优点，并具有良好的经济性，因而在工程中有着广泛的应用[13]，例如应用在汽车的叠板弹簧、重车大梁、双金属板储能弹簧、特殊组合梁等[14-20]。与整梁相比，组合梁的强度和刚度都有所减弱，但具有较好的弹性变形能力，工程中较适宜作弹性消能构件[21]。