高填方土质路基稳定性分析与填筑技术研究

潘 磊,徐申力

（1.丽水市城投基础设施建设有限公司,浙江 丽水 323000; 2.浙江大学建筑设计研究院有限公司,浙江 杭州 310012）

0 引言

随着国内基础交通网络的逐渐完善，各种等级的道路工程建设规模扩大，边坡灾害现象也越来越多。尤其是道路穿越地势起伏较大的山地丘陵地区时，路基填土高度大，不可避免地会出现各种高边坡。工程师在处治高填方路基时，一般是套用相似项目的通用图表，对路基的变形规律认识不够深入，选择的处治方案过于保守，导致工程造价过高。而且高填方路基边坡失稳破坏机理复杂，影响因素较多，计算理论尚不完全成熟，如果对其稳定性分析不当，可能导致道路在运营期间出现滑塌失稳，引起人员伤亡及经济损失[1]。因此，进一步研究高填方土质路基稳定性与填筑技术具有十分重要的工程意义。

1 高填方土质路基稳定性影响因素及分析方法

1.1 高填方路基稳定性影响因素

在城市道路项目建设中，将填土高度＞20 m的边坡定义为高填方路基。由于高填方路基填土压实困难，在设计时必须对其稳定性进行计算，并正确评价边坡的变形特点和破坏形式[2]。

1.2 高填方路基稳定性分析方法

路基边坡稳定性分析技术不断发展，已经由最初的地质现场测绘、工程类比等定性分析方法，发展至各种极限平衡法、数值模拟等量计算方法。

1.2.1 极限平衡法

极限平衡法假设土质高填方路基稳定性为平面应变问题，即先假定滑动面位置及形态，把具有滑动趋势的边坡沿着滑动面按一定的规则划分成若干个特定尺寸块状体，并借助各块状体的平衡条件计算出边坡的整体稳定性。该方法计算模型简单、需要参数少、精确度较高，在工程中应用十分广泛。根据边坡滑动面形态和假设条件的不同，极限平衡法主要包括瑞典圆弧法、简化Bishop法、Janbu法等，各计算方法的特点见表1[3]。

表1 不同极限平衡法特征

根据《城市道路路基设计规范》（CJJ 194—2013），高填方土质路基边坡推荐采用的极限平衡法为简化Bishop法，安全系数Fs计算见式（1）～（2）：

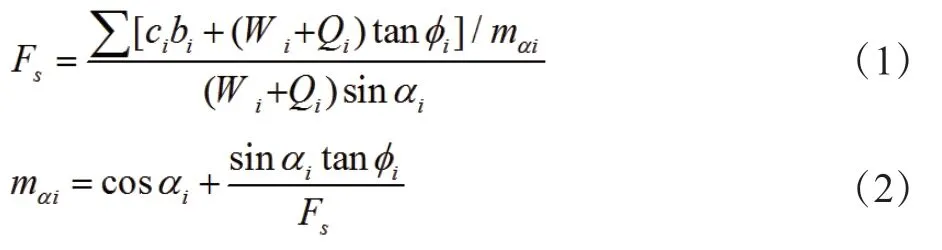
式中，ci——第i个土条所在土层黏聚力（kPa）；φi——第i个土条所在土层内摩擦角（°）；bi——第i个土条的宽度（m）；Wi——第i个土条的重力（kN）；Qi——第i个土条垂直方向外力（kN）；αi——第i个土条底滑面倾角（°）；mαi——计算系数。

1.2.2 数值模拟法

随着计算机运算能力的飞速提升，数值模拟对真实岩土工程问题的模拟运算效率和精确度越来越高。路基边坡稳定性分析中常用的数值模拟方法主要有有限元法、离散单元法、拉格朗日差分法等。相对于极限平衡法，数值模拟法具有成本低、可重复性好的特点，可以在有限的空间和时间内开展大量工况计算，精确控制所研究问题的各个变量，能帮助工程师或科研人员明确岩土体内部的应力应变变化规律机理[4]。

2 不同工况下高填方路基稳定性计算

该文拟采用有限元软件Abaqus2022和理正岩土6.5中内置的极限平衡法来共同分析不同工况下高填方土质路基边坡稳定性，其中有限元法计算是以塑性区贯通状况为失稳判据。

2.1 边坡工程概况

2.1.1 计算参数

该文以某市政快速路为研究对象，路线处于丘陵地带，山高坡陡，沟壑纵横，地形起伏较大。该道路设计速度为100 km/h，路基宽度为34 m，沥青路面结构厚74 cm，所处区域属亚热带湿润区，多年平均气温20.5 ℃，雨水较充足，年平均降雨量为968 mm，主要集中在7—10月份。

高填方土质高边坡段落为K15+225～K15+680，研究断面桩号为K15+660，最大填高28 m。根据地质测绘、钻探、室内土工试验数据等，地基土从上到下分别为粉质黏土、碎石土、基岩，填料为性能良好的砂砾土，不同岩土体的主要物理力学参数为：①粉质黏土容重19 kN/m3、黏聚力23 kPa、内摩擦角20°；②碎石土容重20.5 kN/m3、黏聚力23 kPa、内摩擦角22°；③基岩容重25 kN/m3、黏聚力36 kPa、内摩擦角42°，岩体结构完整，节理裂隙不发育；④砂砾填料容重20 kN/m3、黏聚力5 kPa、内摩擦角 35°。

2.1.2 设计方案

一级、二级和三级边坡坡率分别为1∶1.5、1∶1.75、1∶2，边坡坡面采用拱形骨架防护，右侧采用衡重式挡土墙护脚；边坡两侧设置矩形排水沟，每级平台均设平台截水沟，防止地表水冲刷坡面和下渗；护脚墙墙体设置仰斜式排水孔，如图1所示。

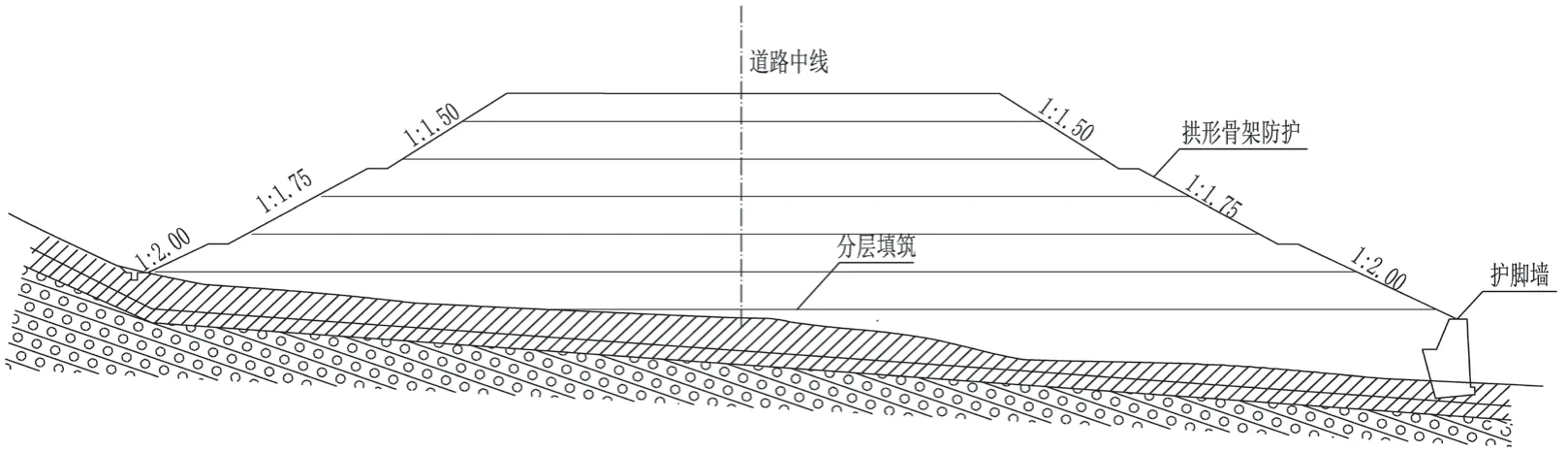
图1 高填方路基边坡设计图

2.2 计算模型建立

2.2.1 极限平衡法计算模型

可将高填方路基的图纸在AutoCAD中另存为DXF文件，导入到理正岩土中即可识别。需要注意，DXF文件中的路基模型线条必须是直线段，不得采用多段线、样条曲线等线条。

2.2.2 有限元模型

单元及屈服准则[5]：道路属条形建筑物，将高填方路基简化为二维模型，利用Abaqus软件中内置的实体solid单元模拟边坡岩土体，屈服准则采用Drucker-Prager本构。同时，采用分层加载的形式模拟高填方路基的分层填筑。

网格划分：在兼顾计算精确度和计算速度的原则下，边坡岩土体采用正四面体网格，坡面单元网格适当加密，尺寸取0.5 m，其他部位网格尺寸取1 m，共划分出1 236个单元，1 574个节点。

边界条件：边坡顶面设置为降雨入渗边界（自由边界），其变形不受约束；模型底部约束x、Y方向位移，模型左右边界约束X方向的位移。

2.3 天然状态下高路基边坡计算结果

2.3.1 不同计算方法下高边坡安全系数

为了验证该边坡设计方案的可行性，笔者利用有限元软件Abaqus和理正岩土计算了天然状态下高填方路基边坡的安全系数，计算结果见表2。

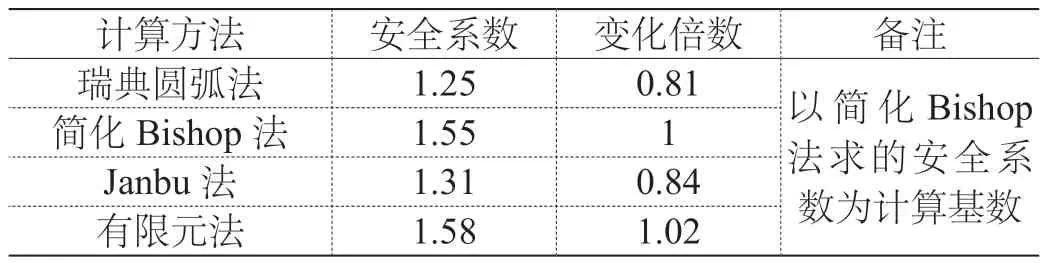
表2 不同计算方法下高边坡安全系数

由计算结果可知，在相同工况下，不同计算方法所得到的高填方路基安全系数并不完全相同，大小顺序为：有限元法＞简化Bishop法＞Janbu法＞瑞典圆弧法。这说明，瑞典圆弧法和Janbu法用于高边坡路基设计偏于保守，可能造成较大的资源浪费。同时，有限元法和简化Bishop法的计算结果相差不大，均满足《城市道路路基设计规范》（CJJ 194—2013）要求。在开展高填方设计时，为了提高验算结果的可靠性，可以采用两种方法对计算结果相互校核。

2.3.2 不同降雨条件下高填方路基安全系数

相关研究表明，80%以上的路基边坡病害都与降雨有关，因此该文也利用有限元法研究了连续降雨条件下高填方路基的稳定性。降雨历时分别为0 h、12 h、24 h、48 h、72 h，降雨强度分别为20 mm/d、50 mm/d、100 mm/d。不同降雨条件下高填方路基安全系数如图2所示。

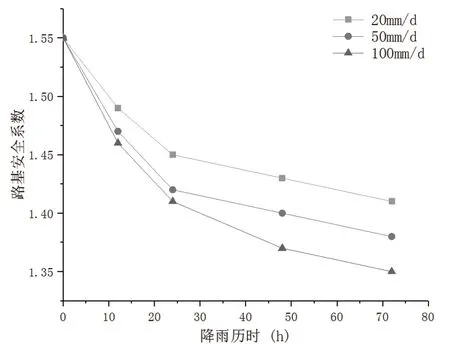
图2 不同降雨条件下高填方路基安全系数

由图2可知：在不同降雨工况下，高填方路基边坡安全系数均大于1.35，满足规范要求，说明原设计方案是合理可行的。此外，在降雨强度相同的条件下，高填方路基边坡的安全系数均随着历时的增加而减小，但减小速率逐渐变缓。当降雨历时＜24 h时，路基边坡安全系数降低速率较快，可达0.004 2/h；当降雨历时＞48 h时，路基边坡安全系数降低幅度不明显。出现上述现象的原因在于[6]：一方面，降雨沿着坡面渗入路基本部，增加填料自身重力，降低填料抗剪强度，即增加边坡下滑力的同时降低了其抗滑力；另一方面，降雨初期，非饱和土会产生渗流动水力，降低边坡稳定性。

3 高填方土质路基填筑技术探讨

高填方土质路基的稳定性与填筑质量密切相关，而含水率和压实度是控制路基填筑质量的关键指标。

3.1 填筑含水率控制

由击实试验可知，土体含水率对其击实效果有很大影响。土体含水率较低时，水分一般是以强结合水的形式存在（水膜较薄），使得土颗粒间的分子引力和摩擦阻力较大，阻碍土颗粒间的相互移动；反之，土体中自由水较多，击实时土颗粒间存在孔隙水压力，削弱击实能量。因此，为了提升高填方土质路基压实质量，提高压实机械工作效率，降低施工成本，应确保路基填料的含水率≈最佳含水率±2%。

路基填料的含水率会随取土区域、季节和降雨量的变化而变化。在降雨量较小的季节，填料含水率＜最佳含水率，路基施工前可通过补水来增加填料含水率。当不存在补水可能或补水成本过高，为了达到规范要求的路基压实度，笔者建议采用路基压实时降低土层摊铺厚度、增加碾压机械能量和碾压次数等方法；在降雨量较大的季节，填料含水率＞最佳含水率，需要翻挖晾晒或掺入水泥、石灰等无机结合料。

3.2 压实度控制

高填方土质路基的压实质量受压实机械及碾压程序的影响较大。

压实机械选择：宜根据填料的类型及抗压强度来选择合适的压实设备，如黏土黏性较强，含水率较高，为了避免出现弹簧土，通常选择轮胎式压路机或凸块压路机；砂土黏性差，水分压实时易进入颗粒孔隙，宜选择静压式压路机；碎石、砂砾土等颗粒间镶嵌效果好，宜采用振动压路机。

碾压程序：为了提升高填方土质路基的施工质量，可采用“三阶段、四区段、八流程”的流水作业方式。路基在碾压过程中应坚持“先慢后快，先边后中，先轻后重”的原则。同时，为防止路基出现漏压现象，相邻两轮道宜重合轮宽的1/3。

3.3 铺筑土工格栅

土工格栅具有强度大、变形小、重量轻等特点，使用在高填方土质路基中可有效分散土体上作用的附加应力，提高其抗剪强度，避免土体出现局部变形过大，可大幅提升高填方路基的整体稳定性。土工格栅铺筑时应保持平整顺直，不得皱折、重叠，两侧宽度与路基同宽。

4 结语

该文研究了高填方土质路基的稳定性影响因素、计算方法、填筑质量控制要点等，并以某道路高填方路基为研究对象，计算了不同工况下的安全系数，主要得到以下结论：①高填方路基稳定性计算可视为平面应变问题，主要计算方法有瑞典圆弧法、简化Bishop法、Janbu法、有限元法等；②高填方路基安全系数会随着降雨强度和降雨历时的增加而减小。瑞典圆弧法计算出的安全系数偏于保守，有限元法和简化Bishop法的计算结果相差不大，可在设计时相互校核；③高填方土质路基填筑时应严格控制填料含水率和压实度，条件允许时可分层铺筑土工格栅提高整体稳定性。