基于合作博弈的产销者社区分布式光伏与共享储能容量优化

王再闯 陈来军 李笑竹 梅生伟,,

基于合作博弈的产销者社区分布式光伏与共享储能容量优化

王再闯1陈来军2李笑竹3梅生伟1,2,3

（1. 新疆大学电气工程学院 乌鲁木齐 830046 2. 青海大学新能源光伏产业研究中心 西宁 810016 3. 清华大学电机工程与应用电子技术系 北京 100084）

含共享储能的分布式光伏产销者社区是提高储能和光伏利用率，降低产销者投资成本的有效途径。社区内部共享储能和分布式光伏的容量配置方案不仅要考虑投资的经济性，还需计及社区内部不同投资主体的利益交互带来的影响。针对上述挑战，提出了基于合作博弈的共享储能与分布式光伏容量协同规划方法。首先，在合作博弈框架下构建分布式光伏产销者、共享储能运营商多方参与者的策略合集与支付函数；其次，分析各参与者在不同合作模式下的均衡策略，利用改进Shapley值法辨识不同参与者对合作收益的贡献度；最后，基于某地实际的光伏数据进行了算例仿真，表明所提模型能够实现博弈各方利益在均衡意义下的最大化，同时保证资源综合及高效利用。

分布式光伏产销者 共享储能 合作博弈 优化配置 分配策略

0 引言

随着“双碳”政策的推动与光伏技术的发展，以产销者社区为主的新型光伏消纳主体得到迅速发展[1-2]。光伏产销者社区不仅可以降低用户的用能成本，还可以促进光伏的就地消纳[3-4]。目前，光伏产销者社区内部投资主体单一，多以配置独立储能为主，造成光伏及储能的实际利用率较低、投资成本较大。利用不同类型产销者的能量产销差异性及充放电需求差异性进行内部电力互补和储能共享，可以进一步提高光伏和储能的利用率，降低投资成本。因此，在投资规划阶段考虑多主体的利益交互与协调互补特性进行分布式光伏与共享储能的容量配置，对推动光储系统的协调发展具有重要的指导意义。

目前，国内外对光伏产销者社区光储容量优化配置已展开了大量研究，根据分布式光伏与储能的结合，大致可以分为以下两种情况。对已有分布式光伏进行储能容量优化配置方面，文献[5]基于内部供需比定价的基础上分别对光伏产销者社区分布式储能和集中式储能进行容量优化配置。文献[6]为解决光伏产销者单独配置储能容量过大问题，建立了两阶段储能容量优化配置方法。在分布式光伏与储能协同规划方面，文献[7]以负荷缺电率为指标，考虑当地的辐照度及环境温度，对独立光伏系统中光储容量进行优化配置。文献[8]在对光伏、储能老化机制评估的基础上，通过经济指标确定光伏-储能的最佳容量配置。以上文献以光伏产销者社区为研究对象，对产销者社区分布式光伏与储能容量优化配置展开研究。其中，储能均是作为被动的调度单元，无法体现储能的独立决策能力。同时，对于储能均是针对光伏产销者独立配置为主，投资成本大，利用率低。为此，亟须研究提升储能灵活性与经济性的新运营模式。

共享储能利用其规模性以及不同用户储能需求的时空互补性，分时复用，有效提升储能的灵活性与经济性[9]。文献[10]提出了共享储能在发电侧应用的一种方法，通过储能的共享来提高各风电场储能资源的灵活性及经济性。文献[11]以共享经济为出发点，探讨了现货市场中储能资源共享情况，并通过非合作博弈的方法建立了共享储能的通用模型。文献[12]借鉴航空等领域的超售运营策略，建立了共享模式下社区分布式光伏与储能的联合运行模型，从而提高储能资源的利用率及社区内用户的用电经济性。文献[13]提出了共享场景下计及用户和储能供应商投资效益的双层储能配置和运营方法，通过容量租赁的方法提高储能资源利用的灵活性。将共享储能作为独立的决策主体引入到产销者社区内部光储容量优化配置中，可以提高分布式光伏及共享储能的利用率，降低产销者的投资成本。然而，随着光伏产销者社区内部产销者类型的增多，各参与者作为独立的决策主体参与分布式光伏与共享储能投资规划时，不同投资主体的利益交互对光储容量的优化配置具有重要的影响。为此，亟须研究兼顾多方利益诉求的分布式光伏与共享储能协同规划方法。

博弈论可准确反映多个决策主体利益交互下的智能决策行为，被广泛地应用于电力系统运行规划中[14-16]，是剖析分布式光伏与共享储能协同规划中多方参与者利益交互的有效手段。文献[14]在点对点交易模式下，通过合作博弈和非合作博弈的方法分析了买方与卖方之间的利益交互关系。文献[15]以微电网缺电率作为可靠性约束，通过非合作博弈和主从博弈的方法优化微电网内部各参与主体的容量配置。文献[16]以光伏微电网群为对象，提出了合作博弈的市场交易模型，以实现不同光伏微电网之间的利益交互问题。

基于上述分析，针对光伏产销者社区内共享储能与分布式光伏容量协同规划时不同投资主体的利益交互问题，建立了合作博弈的光储容量协同规划模型。在光伏产销者社区中引入共享储能和分布式光伏产销者联盟机制，综合考虑不同类型光伏产销者之间充放电需求差异和能量产销特性差异，研究不同投资主体（共享储能投资商-不同类型的光伏产销者）利益交互情况下光储容量的协同规划问题，进一步分析了各参与者不同合作模式下的均衡策略。对联盟的合作收益，考虑各参与者对联盟利益的贡献度，采用改进Shapley值法进行分配。最后，通过仿真验证了本文所提分布式光伏与共享储能协同规划模型的可行性和合理性。

1 社区共享储能系统构建

1.1 分布式光伏产销者社区共享储能系统框架

本文考虑的光伏产销者社区共享储能框架如图1所示。共享储能作为一个独立的决策主体与产销者社区的若干个分布式光伏产销者组成联盟，联盟内的分布式光伏产销者包括居民型光伏产销者、工业型光伏产销者或者商业型光伏产销者。不同类型的光伏产销者利用彼此间的源-荷差异性进行电力交互，同时通过各自充放电需求的互补性与共享储能进行功率交互。

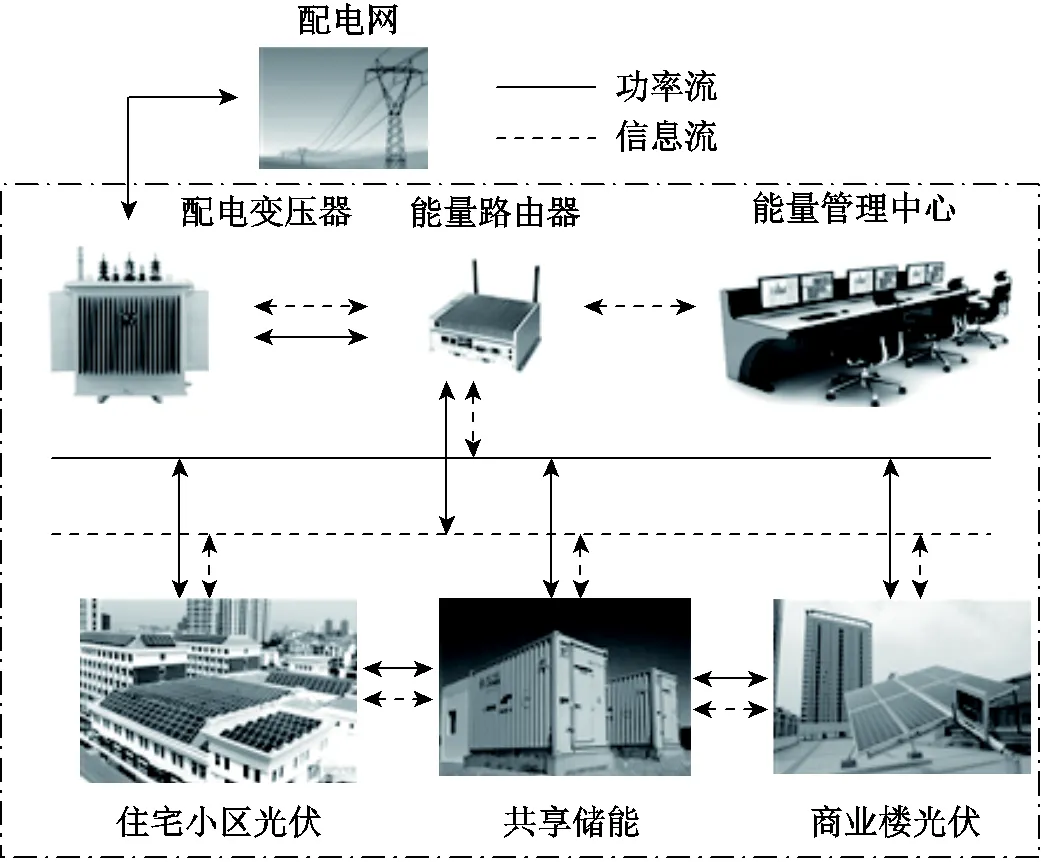
图1 分布式光伏产销者社区共享储能示意图

由图1可知，在光伏产销者社区内部，储能运营商建立一个集中式储能来满足各分布式光伏产销者的储能需求，通过满足不同时刻充放电需求进行获利。联盟内部通过建立自己的电力交易价格机制来约束各参与者的电力交易行为，具体的电力交易由产销者社区的能源管理中心执行。

1.2 含共享储能的分布式光伏产销者社区运行策略

合理的运行策略有助于提高分布式光伏产销者社区的光伏就地消纳能力及储能的利用率。光伏产销者社区内部，每个光伏产销者及储能运营商均配备了智能电能表，用来记录社区内部光伏产销者与储能运营商之间的电量交易情况。产销者与产销者之间，产销者与共享储能之间存在着双边电量交易。不同类型的光伏产销者社区建立各自的光伏发电系统（住宅小区光伏产销者或者商业楼光伏产销者），在满足自身负荷需求后，如果有盈余，首先将多余的电量在其他产销者社区之间进行出售，然后将剩余的功率出售给储能运营商进行充电，最后将剩余的功率出售给电网。同样当产销者出现功率缺额时，首先从其他产销者处购电，其次是储能运营商，最后才是从电网购电。分布式光伏产销者社区具体的运行策略见附录。

2 产销者社区共享储能与分布式光伏产销者电量交易模型

2.1 产销者社区内部电量交易价格设定

在电力交易的过程中，通过交易的价格来约束交易之间的先后顺序。售电时约束为

购电时约束为

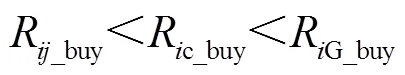
本文的电价采用三段式电价。在峰-平-谷每个时段的购、售电价格都要遵循此价格约束，本文设定电力交易之间的价格差为0.1。

2.2 分布式光伏产销者电量交易模型

分布式光伏产销者的电量交易包括购电和售电两种情况，为了方便下文的表述，设定

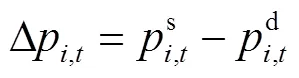
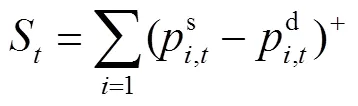
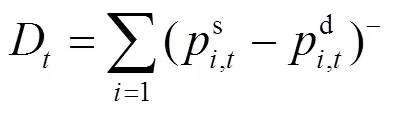
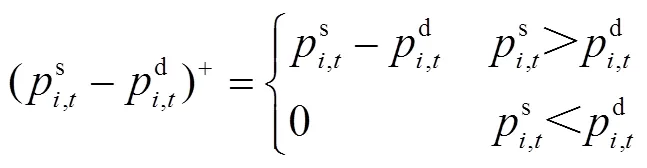
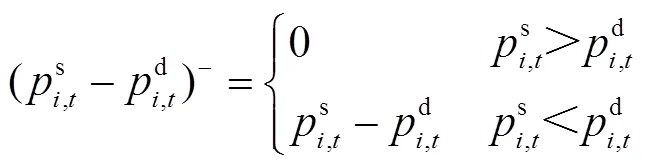
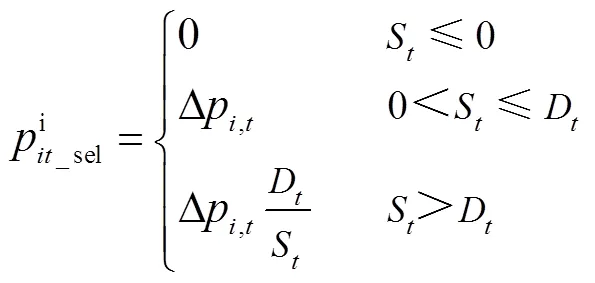
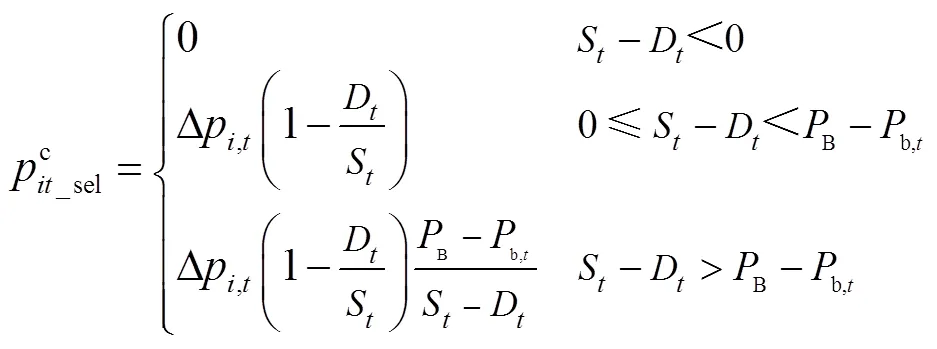
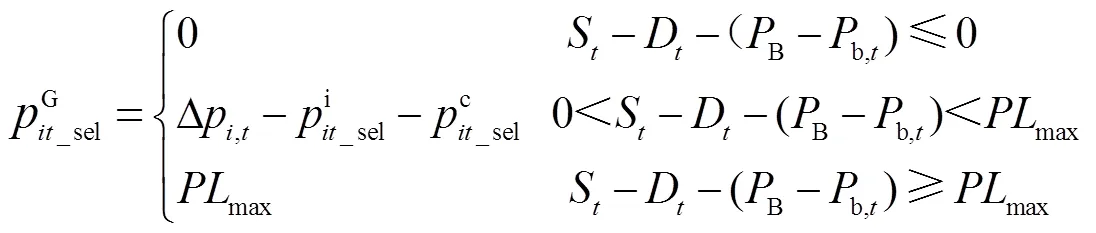
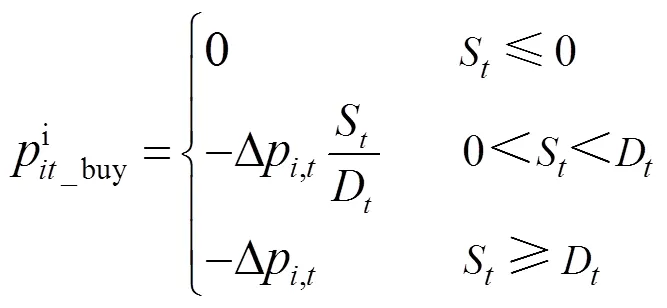
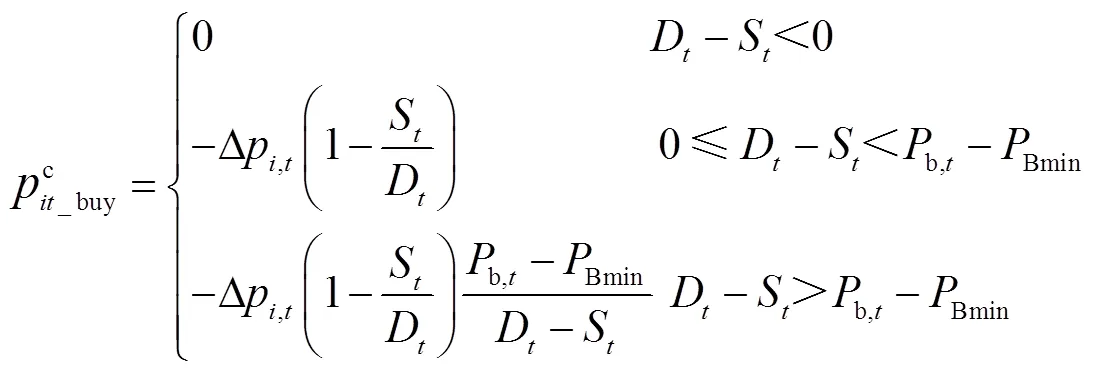
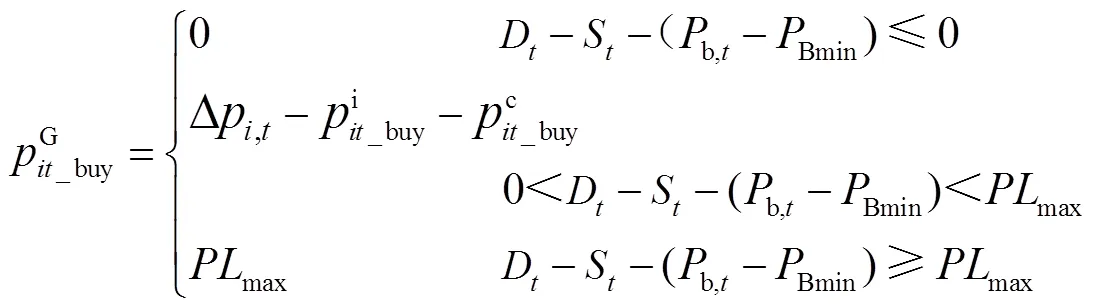
2.3 共享储能电量交易模型

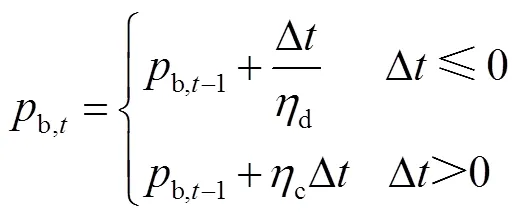
其能量状态约束为

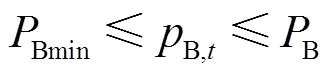
共享储能的购售电量,按照相邻时段的能量状态之差进行计算，即

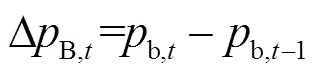
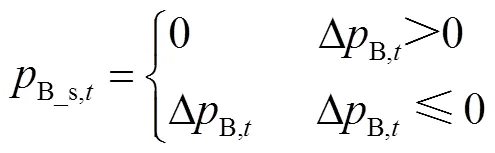
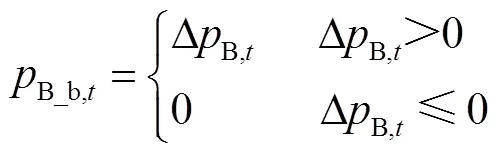
3 合作博弈的共享储能与分布式光伏容量优化配置模型

博弈研究的是多个决策主体在利益相互制约下，理性选择实现自己目标的最优策略的一种行为。其中，常见的非合作博弈侧重于个体理性，合作博弈侧重于集体理性，主从博弈侧重于决策的先后顺序[17]。本文分布式光伏与共享储能容量协同优化涉及不同投资主体的利益交互，可以通过有强制性的合作协议实现共赢，因此采用合作博弈的方法对分布式光伏和共享储能的容量进行优化配置。

3.1 参与者及其策略

光伏产销者社区内部，储能运营商建立集中式共享储能，各分布式光伏产销者共同使用。因此，本文合作联盟的参与者为各光伏产销者及共享储能运营商。

联盟通过决策分布式光伏产销者的容量和共享储能的容量来最大化各自的收益。具体如下：

3.2 参与者支付及特征函数

本文将参与者的支付定义为年收益与年费用之差，包括售电收入、财政补贴收入（本文将财政补贴以电价系数的形式体现）、报废收入、购电成本、投资成本、运行维护成本。

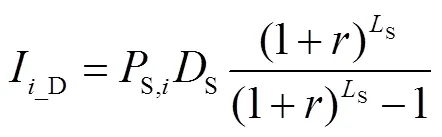
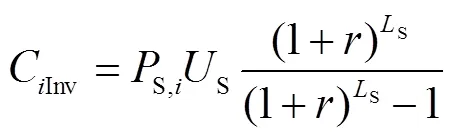
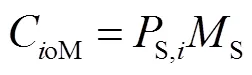
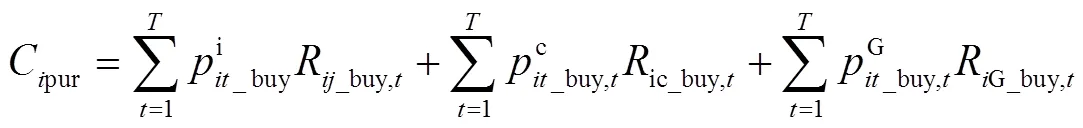
3.2.2 共享储能运营商的支付

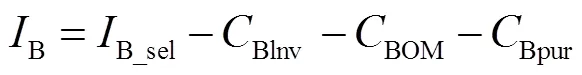
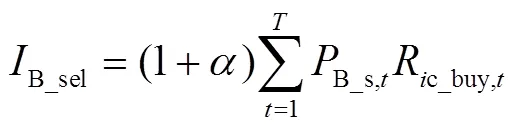
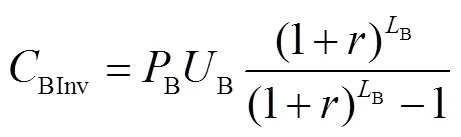
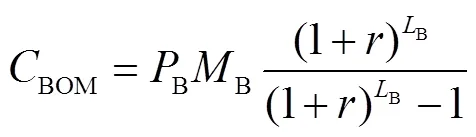
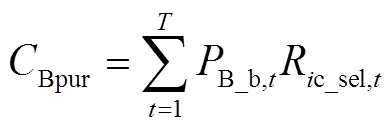
式中，B为共享储能的储能容量；B为共享储能单位容量的投资费用；B共享储能单位容量的维护费用；B为储能的寿命。

3.2.3 特征函数

本文所建的合作博弈模型是特征函数博弈，联盟的收益依赖于参与者自身的行动并且可以在参与者内部及进行分配，本文的特征函数定义为联盟中成员合作创造的额外收益。

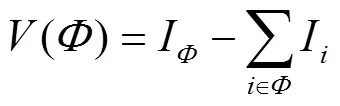
3.3 分配策略

3.3.1 常规Shapley值分配策略

Shapley值是基于联盟内部各成员的边际贡献进行分配的一种方式[17]。其中，边际贡献表示参与者加入联盟前后特征函数的差值，关注的是每一个参与者的边际收益，如式（31）所示。该方式很好地体现了各成员对联盟的边际贡献程度，具体公式如式（32）所示。

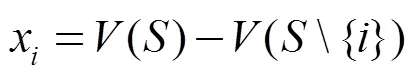
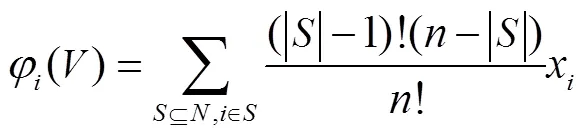
3.3.2 改进Shapley值分配策略

常规的Shapley值分配策略，联盟内部的各参与者具有相同的权重，是理想化情况的一种分配，难以反映不同参与者的个体差异性，尤其是在不同类型光伏产销者与共享储能的合作联盟中，其个体差异性更加明显。为了保证分配结果的公平合理性，维持合作联盟的稳定性，基于参与者的个体差异性，在进行利润分配时除了考虑边际贡献，还应考虑每个参与者对整个联盟的利润贡献度。定义联盟中利润贡献度取决于各种组合下其参与联盟前后收益增量与联盟整体收益增量之比，即

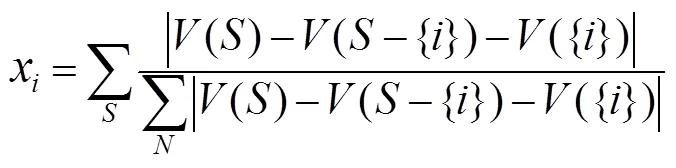
得出联盟内参与者的新权重为

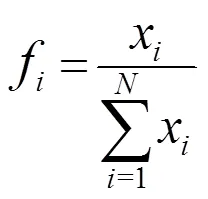
得出参与者的新权重与旧权重之差为

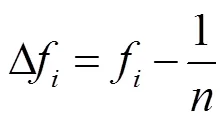
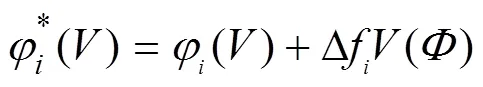
3.4 求解流程

本文采用粒子群算法通过迭代搜索的方法对不同博弈模式下的均衡点进行求解，设置种群个数为100，迭代次数500，具体的求解流程如图2所示。

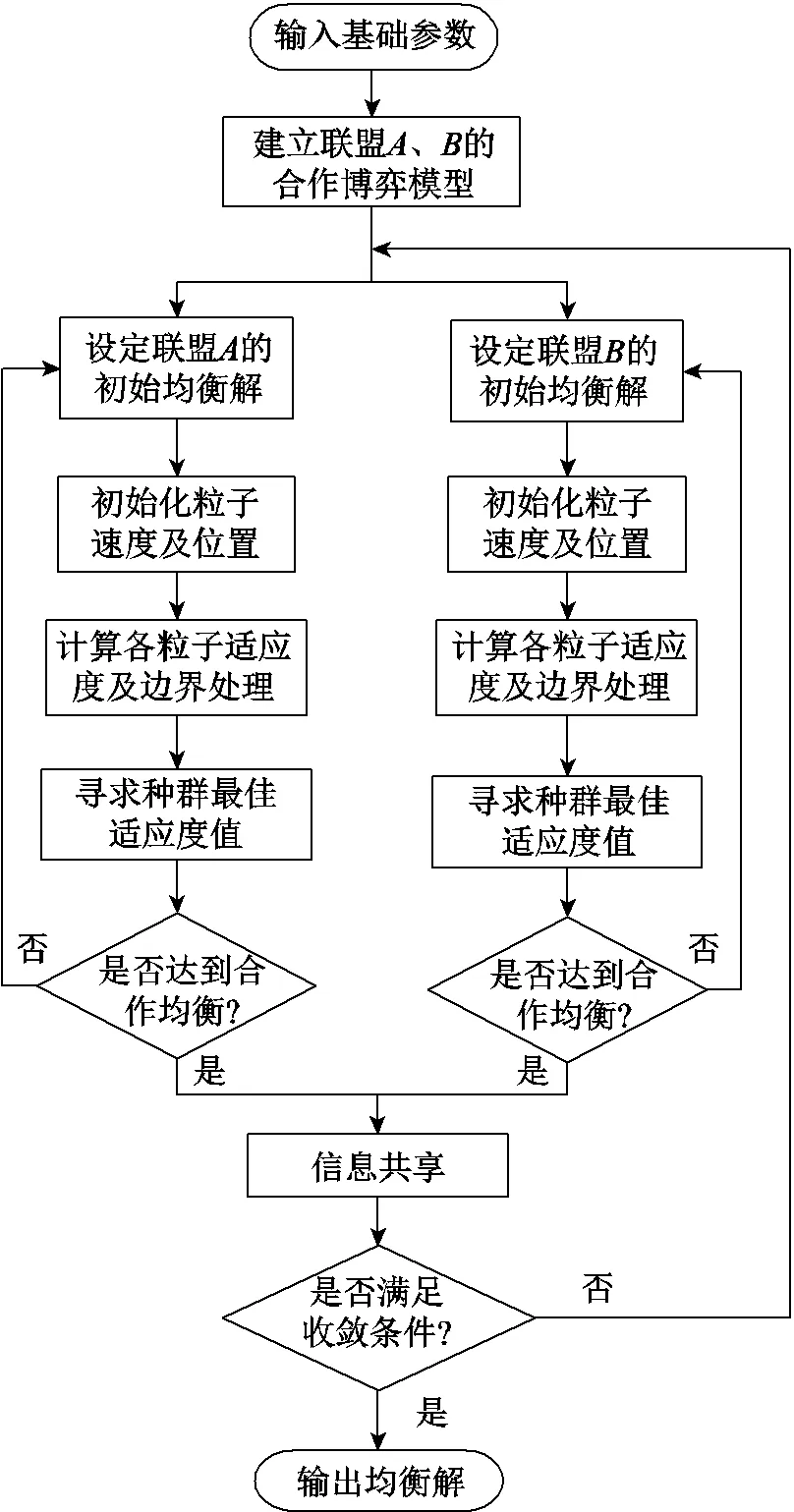
图2 博弈均衡点求解流程

4 算例仿真

4.1 参数设置

采用某地实测光伏数据对本文所提的规划方法进行仿真验证。分布式光伏系统[17]及储能系统关键参数[18]见表1。分布式光伏产销者和共享储能从电网购电时采用三段式电价，高峰时段（10:00～15:00，18:00～21:00），平时段（7:00～10:00，15:00～18:00，21:00～23:00）和低谷时段（23:00～7:00），联盟内部各参与者之间的能量交易服从本文的价格约束。

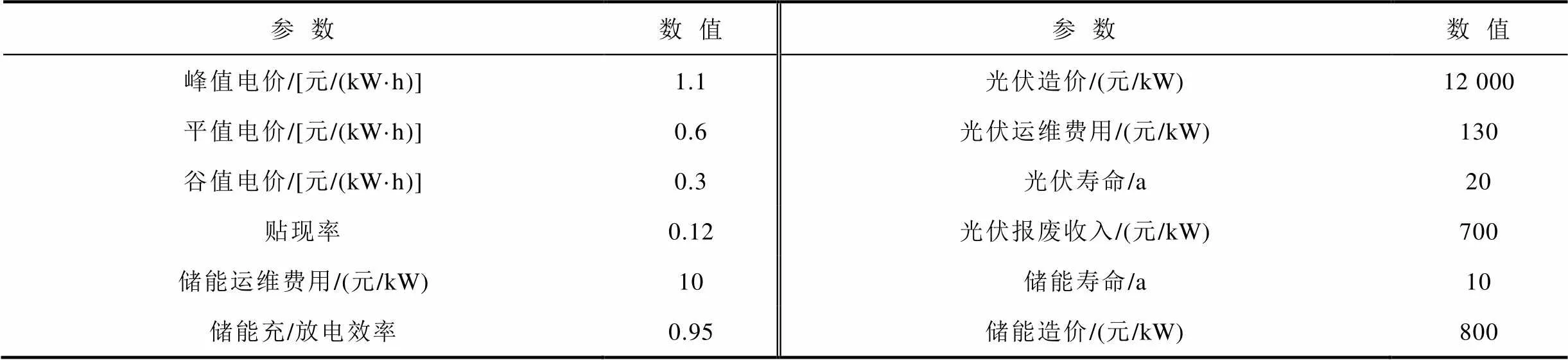
表1 关键参数

4.2 不同博弈模式均衡结果及支付分析

不同博弈模式均衡结果及其支付见表2，其中M为分布式光伏产销者1、N为分布式光伏产销者2、B为共享储能运营商。

表2 不同博弈模式的均衡结果及其对应策略下的支付

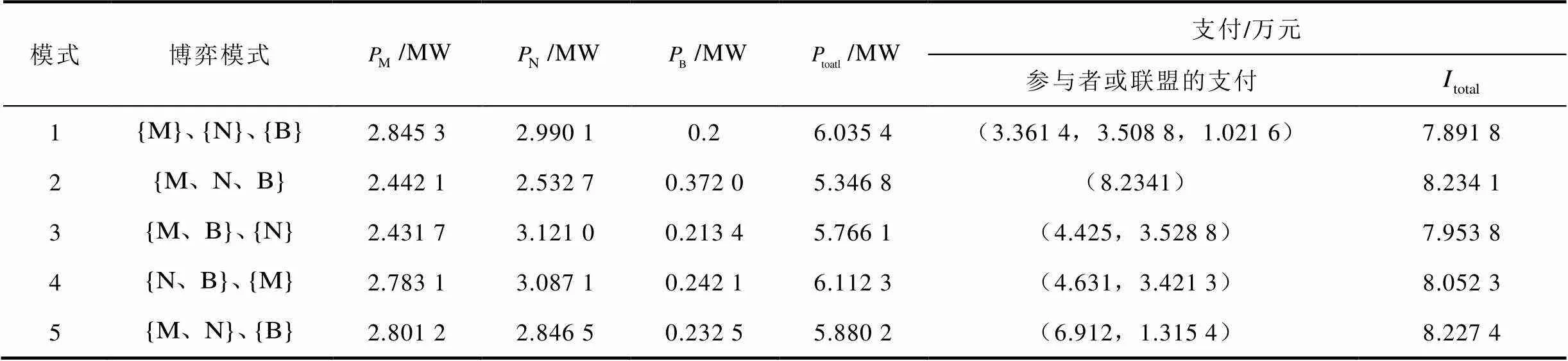
Tab.2 Results of equilibrium and its payment under the corresponding policy

表2中的结果表明，五种博弈模式下均衡结果既有相似性又有差异性。相似性体现在对于每种博弈模式都有N＞M＞B，即产销者2的光伏容量大于产销者1的光伏容量大于共享储能的容量。原因在于产销者2为商业办公楼，在光伏出力较大的时段，负荷也较大，其负荷特性和光伏出力特性基本一致。产销者1为居民用户，只有在早晚时段负荷较大，他时段负荷较小，从而其光伏出力可以填补产销者2的光伏出力差额，在满足自己负荷的条件下卖给产销者2、共享储能以及电网，从而以相对较小的光伏容量下即可实现自己的收益；相反产销者2的基本负荷较大，并且其负荷特性和光伏出力特性基本一致，因此要通过售电实现收益，所建的光伏容量相对较大。

差异性主要体现在各联盟的总容量以及总支付不同，模式1三者处于完全竞争的模式下，此时配置的总容量最大，但总的支付却是最小。模式2三者处于完全合作模式，此时配置的总容量是最小，其支付却是最大，实现了收益的最优。对于其他部分合作的博弈模式，优化结果介于两者之间。

表2的仿真结果显示，竞争程度的高低将会影响各独立决策者的决策行为以及所得到的收益。

4.3 联盟稳定性分析

根据式（30）、式（31）结合表2可得不同联盟型博弈的特征函数及边际贡献，具体求解过程如附录，结果见表3。

表3 特征函数与边际贡献

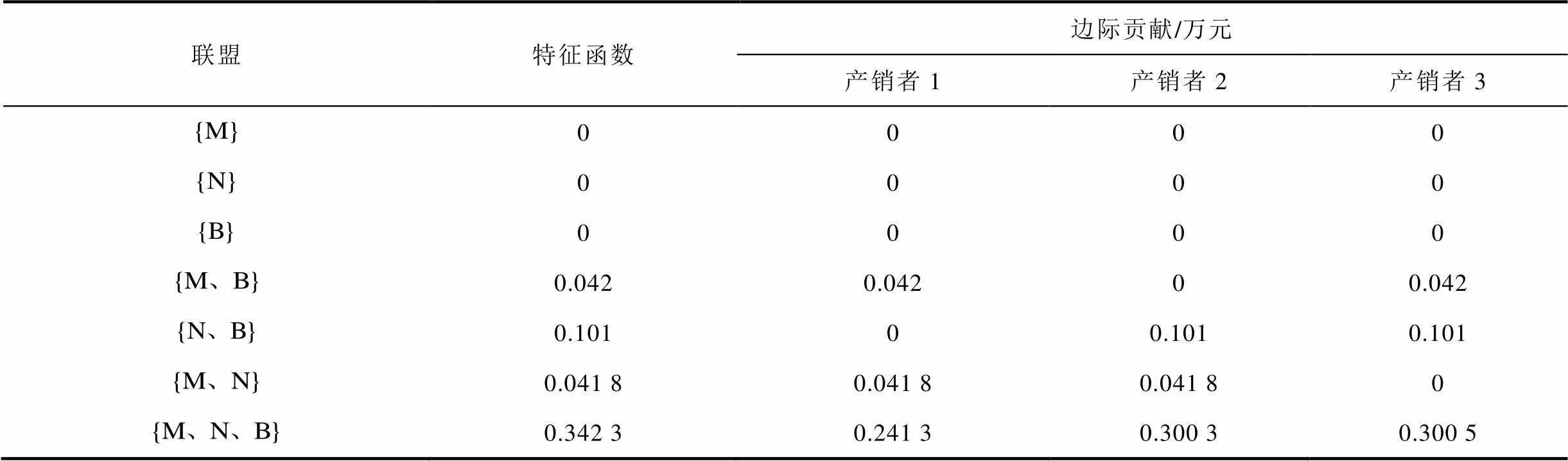
Tab.3 Characteristic functions and marginal contributions

社区内分布式光伏产销者通过结盟的方式进行储能共享时，总联盟必须在满足整体理性和个体理性的条件下才能结成稳定的联盟。然而，对于一个参与者而言，联盟的收益不是本质，参与者个体的收益才是本质[15]，即分布式光伏产销者和共享储能结成联盟并通过联盟获益，但联盟内部每个成员仍需要遵循个体理性，以追求自身利益最大化为目标。

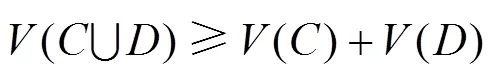
4.4 合作收益分配分析

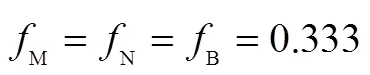
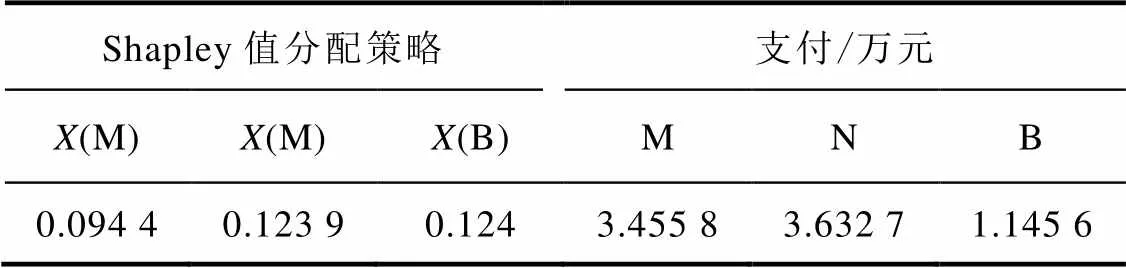
表4 常规Shapley值的分配策略

表5 基于改进Shapley值的分配策略

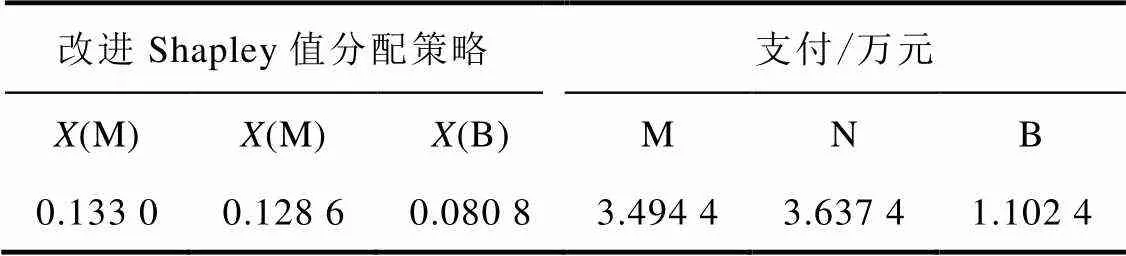
Tab.5 Allocation strategies based on modified Shapley values

结合表4和表5可知，与常规Shapley值法相比，采用改进Shapley值法进行分配时光伏产销者的分配有所增加，储能运营商的分配有所减少。作为合作联盟的参与者，产销者1和产销者2承担着社区的主要供电任务，对联盟整体带来的利润贡献度最大，因此其利润贡献度因子的权重较高；而储能运营商只起到辅助作用，其收益主要来自于充放电过程的套利，相对产销者而言给联盟整体带来的利润贡献度较小。改进Shapley值分配方法正是基于参与者对合作联盟利益的贡献度对常规Shapley分配结果进行的修正，修正后的结果更加公平合理，有利于维持合作联盟的稳定性。

4.5 合作联盟内部电力交互情况分析

合作联盟内部，通过不同类型光伏产销者（居民型和商业型）源-荷差异性及充放电行为的互补性，提高光伏及储能资源的利用率，降低产销者的投资压力。为了分析光伏产销者社区内部不同投资主体间的功率交互情况，以夏季某一典型日为对象对联盟内部各参与者功率交互情况进行分析，如图3所示。

图3 联盟内部各参与者功率交互

如图3所示，5:00～7:00时段，产销者1有多余的光伏出力与产销者2进行功率交互；7:00～8:00时段，产销者1与产销者2进行功率交互外，剩余的光伏出力对共享储能进行充电；9:00～14:00时段，产销者2与产销者1进行功率交互，其中10:00～13:00时段，产销者2光伏出力较大，在满足产销者1的功率交互需求外对共享储能进行充电；19:00～21:00时段，为峰谷电价时段，此时无光伏出力，利用共享储能放电满足产销者1和产销者2的用电需求。联盟内部不同参与者之间的功率交互情况，表明本文所建合作博弈模型能够促进光伏出力在社区内部的交互，改变了传统分布式光伏“自产自销，余电上网”的消纳模式，提高了分布式光伏的就地消纳能力。

4.6 与常规多目标优化对比分析

为突出本文所提合作博弈方法的有效性，在经济性目标的基础上引入可靠性目标作为多目标函数对分布式光伏与共享储能进行容量配置。常规多目标函数规划方法与不同博弈模式下的均衡对比结果具体如图4所示。

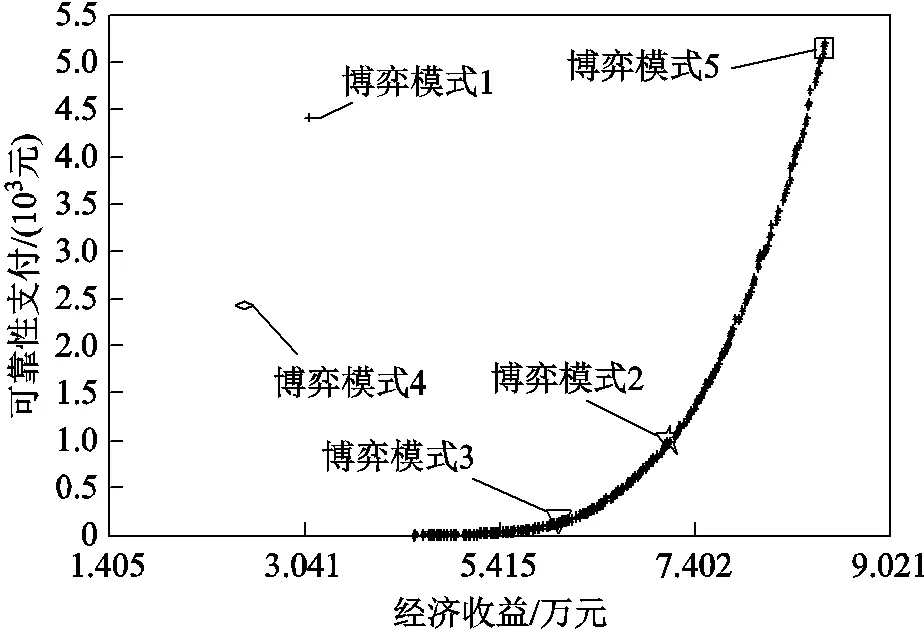
图4 多目标优化与不同博弈模式下的优化结果对比

由图4可知，通过多目标优化方法所得的Pareto最优解不能包含所有博弈模式下的均衡解，如博弈模式1、博弈模式4的均衡解均落在Pareto最优解前沿之外。而实际情况中，这两种博弈模式是真实存在的。因此，与不同博弈模式的均衡结果对比，采用多目标优化时忽略了联盟内部各参与主体的独立决策能力，无法完全体现不同主体的利益交互。

4.7 参数灵敏度分析

表1中的参数大小均会影响博弈的均衡结果，但对均衡产生直接影响的参数为电价和贴现率。

1）电价对均衡点的影响

为分析电价高低对均衡的影响，分别取电价为t1（峰=1.0，平=0.5，谷=0.2），t2（峰=1.2，平=0.7，谷=0.4）计算各自的均衡，并和实时电价下的均衡结果进行对比，结果如图5所示。

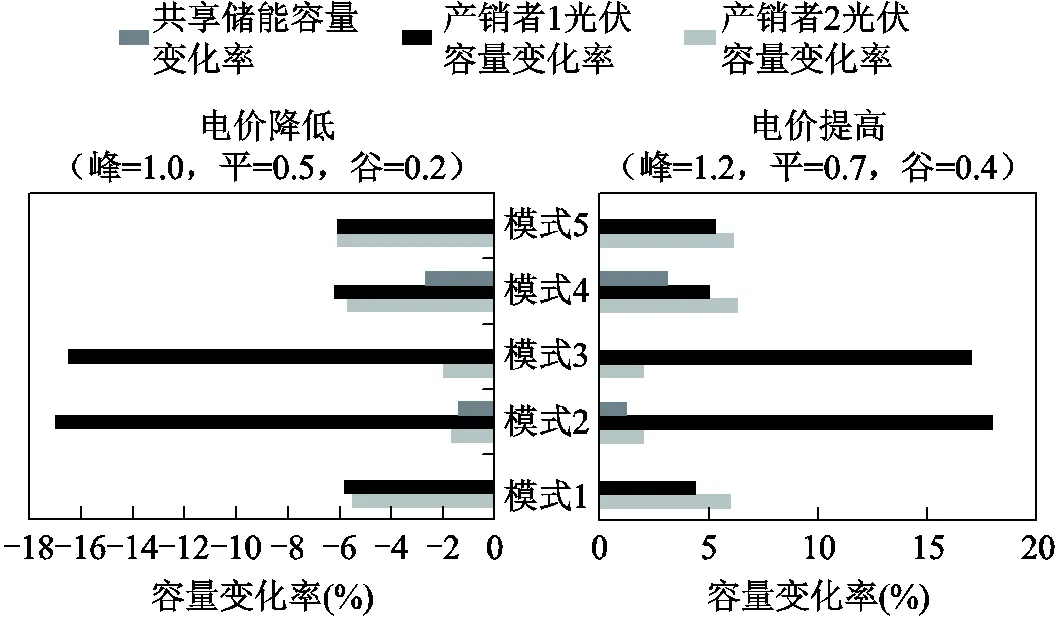
图5 不同电价下均衡结果的对比情况

由图5可知，不同博弈模式下的均衡结果与价格成正相关性。对于产销者1和产销者2来说，其受价格影响的程度较大，对价格的变化最为敏感。对于共享储能其均衡受价格的影响较小。原因在于，对于分布式光伏产销者而言其收益的来源主要是售电收入，售电价格对产销者的收益有最直接的影响，而储能的收益的主要来源于充、放电能量的套利，受到电价的影响较小。

2）贴现率对均衡点的影响

为分析贴现率高低对均衡的影响，分别取= 0.11、=0.13计算其均衡结果，并和=0.12时的均衡进行对比，具体结果如图6所示。

图6 不同贴现率下的均衡结果对比情况

由图6可知，不同博弈模式下的均衡结果与贴现率呈负相关性，且两个光伏产销者光伏容量配置对贴现率的大小最为敏感，共享储能的容量配置受到贴现率的影响较小。原因在于，贴现率是将未来的资产折算成现值的一种体现，在折算过程中要考虑的风险因素较多，相对储能运营商，光伏产销者承担着产销者社区主要的供电任务及联盟的主要收益来源，有较大的投资风险，对贴现率的大小最为敏感。

5 结论

本文针对含共享储能的分布式光伏产销者社区建立了一种基于合作博弈的共享储能与分布式光伏容量协同规划方法，通过理论和仿真可以得出如下结论：

1）引入产销者社区内部电力交易机制及合作博弈的光储容量协同规划模型，合理地模拟了不同投资主体利益交互下分布式光伏与共享储能的容量配置情况，实现资源的优化利用，为各市场主体的投资决策提供必要的价值信息。

2）对不同博弈模式下的均衡及支付进行了对比分析，就完全合作模式与完全对抗模式而言，总支付提高了4.16%，而总容量降低了2.57%。说明本文所提的合作博弈模型实现了资源的合理利用，达到了效益最优。

3）改进Shapley值法在考虑不同参与者个体差异性因素下，通过各参与者对合作联盟收益贡献度对分配权重进行调整。与常规Shapley值法比较，光伏产销者分配结果分别提高了1.26%和0.13%，共享储能分配结果降低了3.77%，使得分配结果更加公平。

4）通过对价格及贴现率灵敏度分析得出，电价与均衡结果呈正相关，贴现率与均衡结果呈负相关。

附 录

1.分布式光伏产销者社区运行策略

附图1 分布式光伏产销者社区运行策略

App.Fig.1 Distributed PV-prosumer community operation strategy

2. 不同联盟型博弈的特征函数求解

根据式（30）并结合表2可得不同联盟型博弈的特征函数值，具体求解结果如下。

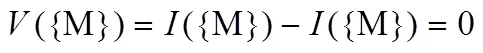
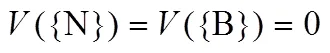
对于边际贡献的求解，根据式（31）结合表2可求解，此处不在多做赘述。

[1] 陈国平, 董昱, 梁志峰. 能源转型中的中国特色新能源高质量发展分析与思考[J]. 中国电机工程学报, 2020, 40(17): 5493-5505.

Chen Guoping, Dong Yu, Liang Zhifeng. Analysis and reflection on high-quality development of new energy with Chinese characteristics in energy transition[J]. Proceedings of the CSEE, 2020, 40(17): 5493-5505.

[2] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.

Zhuo Zhenyu, Zhang Ning, Xie Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.

[3] 张迪, 苗世洪, 周宁, 等. 分布式发电市场化环境下各交易主体响应行为模型[J]. 电工技术学报, 2020, 35(15): 3327-3340.

Zhang Di, Miao Shihong, Zhou Ning, et al. Research on response behavior model of trading entities considering the marketization environment of distributed generation[J]. Transactions of China Electrotechnical Society, 2020, 35(15): 3327-3340.

[4] 涂青宇, 苗世洪, 张迪, 等. 分布式发电市场化环境下基于价格型需求响应的农村光伏交易模式研究[J]. 电工技术学报, 2020, 35(22): 4784-4797.

Tu Qingyu, Miao Shihong, Zhang Di, et al. Research on rural photovoltaic trading pattern based on price-based demand response under marketization environment of distributed generation[J]. Transactions of China Electrotechnical Society, 2020, 35(22): 4784-4797.

[5] Rodrigues D L, Ye Xianming, Xia Xiaohua, et al. Battery energy storage sizing optimisation for different ownership structures in a peer-to-peer energy sharing community[J]. Applied Energy, 2020, 262: 114498.

[6] Huang Pei, Sun Yongjun, Lovati M, et al. Solar-photovoltaic-power-sharing-based design optimization of distributed energy storage systems for performance improvements[J]. Energy, 2021, 222: 119931.

[7] 胡国珍, 段善旭, 蔡涛, 等. 基于液流电池储能的光伏发电系统容量配置及成本分析[J]. 电工技术学报, 2012, 27(5): 260-267.

Hu Guozhen, Duan Shanxu, Cai Tao, et al. Sizing and cost analysis of photovoltaic generation system based on vanadium redox battery[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 260-267.

[8] Hernández J C, Sanchez-Sutil F, Muñoz-Rodríguez F J. Design criteria for the optimal sizing of a hybrid energy storage system in PV household-prosumers to maximize self-consumption and self-sufficiency[J]. Energy, 2019, 186: 115827.

[9] 陈岑, 武传涛, 康慨, 等. 基于改进Owen值法的分布式储能双层合作博弈优化策略[J]. 中国电机工程学报, 2022, 42(11): 3924-3936.

Chen Cen, Wu Chuantao, Kang Kai, et al. Optimal strategy of distributed energy storage two-layer cooperative game based on improved Owen-value method[J]. Proceedings of the CSEE, 2022, 42(11): 3924-3936.

[10] 孙偲, 陈来军, 邱欣杰, 等. 基于合作博弈的发电侧共享储能规划模型[J]. 全球能源互联网, 2019, 2(4): 360-366.

Sun Cai, Chen Laijun, Qiu Xinjie, et al. A generation-side shared energy storage planning model based on cooperative game[J]. Journal of Global Energy Interconnection, 2019, 2(4): 360-366.

[11] Kalathil D, Wu Chenye, Poolla K, et al. The sharing economy for the electricity storage[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 556-567.

[12] 叶晨, 王蓓蓓, 薛必克, 等. 考虑超售的共享分布式光储混合运营模式协同策略研究[J]. 电工技术学报, 2022, 37(7): 1836-1846.

Ye Chen, Wang Beibei, Xue Bike, et al. Study on the coordination strategy of sharing distributed photovoltaic energy storage hybrid operation mode considering overselling[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1836-1846.

[13] He Hongjie, Cheng Liang, Zhu Huan, et al. Optimal capacity pricing and sizing approach of cloud energy storage: a Bi-level model[C]//2019 IEEE Power & Energy Society General Meeting, Atlanta, GA, USA, 2019: 1-5.

[14] Mei Shengwei, Wang Yingying, Liu Feng, et al. Game approaches for hybrid power system planning[J]. IEEE Transactions on Sustainable Energy, 2012, 3(3): 506-517.

[15] 葛少云, 李吉峰, 刘洪, 等. 考虑智能建筑特性的多微网端对端能量交易方法[J]. 电力系统自动化, 2021, 45(6): 203-214.

Ge Shaoyun, Li Jifeng, Liu Hong, et al. Peer-to-peer energy trading method for multiple microgrids considering characteristics of smart building[J]. Automation of Electric Power Systems, 2021, 45(6): 203-214.

[16] 刘念, 赵璟, 王杰, 等. 基于合作博弈论的光伏微电网群交易模型[J]. 电工技术学报, 2018, 33(8): 1903-1910.

Liu Nian, Zhao Jing, Wang Jie, et al. A trading model of PV microgrid cluster based on cooperative game theory[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1903-1910.

[17] 梅生伟, 刘锋, 魏韡. 工程博弈论基础及电力系统应用[M]. 北京: 科学出版社, 2016.

[18] Lombardi P, Schwabe F. Sharing economy as a new business model for energy storage systems[J]. Applied Energy, 2017, 188: 485-496.

Capacity Optimization of Distributed PV and Shared Energy Storage of Prosumer Community Based on Cooperative Game

Wang Zaichuang1Chen Laijun2Li Xiaozhu3Mei Shengwei1,2,3

（1. College of Electrical Engineering Xinjiang University Urumqi 830046 China 2. New Energy Photovoltaic Center of Qinghai University Xining 810016 China 3. Department of Electrical Engineering Tsinghua University Beijing 100084 China）

Distributed PV-prosumer community with shared energy storage is an effective way to improve the utilization of energy storage and PV , reduce the investment costs of prosumers. Capacity configuration schemes for shared energy storage and PV within communities need to consider the impact of investment economics and the interaction of the interests of different investment agents. Aiming at this challenge, a collaborative planning method of shared energy storage and distributed PV based on cooperative game is proposed .First, the strategy set and payment function of distributed PV-prosumers and shared energy storage operators are constructed in the framework of cooperative game. Second, the equilibrium strategies of each player under different cooperation models are analyzed, and the improved Shapley value method is used to identify the contribution of different player to the cooperation benefits. Finally, a simulation is carried out based on the actual PV data of a certain place, which shows that the proposed model can maximize the interests of all players and ensure the comprehensive and efficient utilization of resources.

Distributed PV-prosumer, shared energy storage, cooperative game, optimal configuration, allocation strategy

10.19595/j.cnki.1000-6753.tces.220431

TM731

国家自然科学基金资助项目(52077109)。

2022-03-28

2022-04-30

王再闯 男，1988年生，博士研究生，研究方向为新能源发电与储能技术。E-mail：714553929@qq.com

陈来军 男，1984年生，博士，教授，研究方向为新能源发电与储能技术。E-mail：chenlaijun@qhu.edu.cn（通信作者）

（编辑 赫蕾）