基于弹性优化机制的社区负荷EV分群优化策略
段俊东,黄泓叶,王帅强
(河南理工大学 电气工程与自动化学院,河南 焦作 454003)
随着化石能源的日益枯竭,全球开始积极推进可再生能源的发展[1-2]。人们对新能源的普遍关注拓展了电动汽车(Electric-Vehicle,EV)的销售市场,提高了EV的使用率。但在EV高渗透的社区,车辆的无序充电不仅加剧了电网峰谷差[3],车辆的负荷特性还会对电网造成冲击,影响电网运行的安全性[4],具体表现为配电网峰谷差增大、电网电能质量水平降低等[5-6]。在车辆到电网(Vehicle-to-Grid,V2G)技术的背景下,EV的应用场景得到了转换。通过控制EV合理充放电能够在一定程度上缓解负荷尖峰问题。文献[7]提出以满足调峰需求和用户经济效益的多目标EV优化调度方案,协调优化了客户和系统,满足了运营商峰值负载控制需求。文献[8]考虑了居民峰谷分时电价背景下的日负荷曲线,提出了包含功率限制的居民EV有序充放电策略。文献[9]提出了基于用户需求的居民小区EV充放电优化控制策略,有效防止了变压器过载,降低了小区峰值。文献[10]考虑了天气因素对V2H微网调度影响,建立了源荷联动数学模型。文献[11]提出了一种V2G和G2V的协调模型,以家庭和工作区域为执行单位来优化负荷。文献[12]提出了一种基于PEV功率调度的平滑居民负荷用电负荷曲线的监控策略。文献[13]基于分时电价提出了动态非合作博弈的主从博弈模型,以分时电价为主体引导EV参与入网优化。文献[14]提出EV分群优化的调度策略,该策略根据车辆的不同状况划分车群,分配可调控车群入网调峰。
事实上,若将EV仅作为调度载体则降低了EV的可用度。上述文献在制定相关策略时较少考虑车辆出行需求。针对上述问题,本文提出了基于弹性优化机制的社区负荷EV分群优化策略。该策略以EV返程时刻为标准来划分社区序列,并考虑了车主意愿及车主的用车需求,与用户签订具有弹性限度的合约,并通过分群调控EV充放电计划来优化各社区序列负荷。仿真结果表明,该策略的实施使得社区负荷曲线更加平滑,满足了用户用车需求,减少了用户费用支出,提升了调峰的灵活性。
1 问题引入
EV无序充电时段容易叠加基础负荷峰值时间,进一步加剧负荷尖峰量[15]。通过Monte Carlo法模拟EV无序充电对家庭负荷的影响结果如图1所示。

图1 EV无序充电对家庭负荷的影响
由图可知,在EV无序充电负荷的影响下,相较于EV无序充电前,当日家庭负荷峰谷差增加了约2.66%。从社区层面来看,若社区内的EV进行大规模无序充电会增加社区的负荷量,若对其不加以控制,将严重影响电网的稳定运行。因此,以家庭为单位划分社区负荷序列,模块化管理社区并与用户达成合作协议,采用V2G技术调控EV有序充放电,可分散、独立优化社区各序列负荷,从局部降低社区负荷整体峰谷差,具有一定的现实意义。
2 基于弹性优化机制的社区负荷EV分群优化策略
2.1 社区序列和EV车辆序列的建立
当社区的EV数量较多且无法准确预估车辆返程时间时,对车辆进行集中统一管理的难度较大。本文遵循车主的出行规律,以EV返程时间为标准将社区和EV划分多个管理序列,并通过社区序列模块化管理对应归属的EV序列。通过分析美国家庭交通出行调查数据后发现,可用以下概率密度函数来表示EV返程时刻[16]

(1)
式中,t为返程时刻;μs=17.6;σs=3.4。对应的返概率分布如图2所示。

图2 返程概率分布
EV的日行驶距离会随着用车情况的不同而产生显著的差异,但可用以下概率密度函数进行预估
(2)
式中,σD=3.2;μD=0.88。该概率密度函数如图3所示。

图3 日行驶距离概率分布
基于图2所示的概率分布情况,社区序列的划分如图4所示。其中,EV序列由与对应序列号相同的社区负荷序列进行管控。

图4 社区负荷和EV序列
2.2 获取车辆信息及社区负荷信息
当EV未返回小区充电时,电网侧需要预测EV的充电能量需求,并通过预测的能量需求计算EV可分配的电池容量,进而制定EV的充放电计划和供电计划。具体操作步骤为:
步骤1根据EV的出行规律及充电站的历史充电记录来预测各时刻EV返程车辆数目,记为n;
步骤2电网侧根据预测信息序列号将当前车辆序列号记为x=[x1,x2,…,xn]。此外,电网侧预测该时刻车辆当前电池剩余可用容量,记为E=[E1,E2,…,En];
步骤3电网侧根据上述信息预划分如图4所示的社区负荷序列和车辆序列。同时,电网侧根据社区负荷序列的历史负荷信息预测各社区负荷序列的负荷γ=[γ1,γ2,…,γn],并做好供电规划。
2.3 EV分群与用户合约签订
对于有意愿参与本文所提策略的用户,电网侧依据用户意愿签订车辆和家庭合约,通过车辆的充放电调控家庭用电负荷量并予以车主放电奖励;对于不愿参加策略的用户,电网侧依然需要保证车辆的充电需求。根据车主是否参与策略,在电网侧预划分序列的基础上,将车辆重新划分为策略响应车群和普通车群,并进行独立管控。本文设社区用户车辆数为N,签约人数为N1,则签约率m=N1/N。对于签约的用户,电网提供两种合约可供用户选择。
2.3.1 合约A
(1)考虑到用户早用车需求,合约A在保证一定的合约执行时间下,允许用户在早用车时刻解约。设用户早用车时刻为e1,用户返程时刻为s1,即用户在s1时刻返程,在e1时刻有意愿解约,则用户解约后该车辆对应社区负荷序列下的家庭一并解除合约,并分离出当前社区负荷序列,该家庭负荷同样计及至社区负荷序列。其中,1≤s1 (2)设用户返程时刻为s2,规定解约时刻记为e2,当到达规定解约时间时签约用户可自行解约。同时,电网侧需要预留未签约用户车辆的充电量,但未签约用户的车辆和家庭需要独立管理并建立新的社区负荷序列和车辆序列,并由新的社区负荷序列提供该部分车辆电能需求。其中,s1≤s2 (3)为保证电网侧利益,合约中规定未到达解约时间或解约条件,用户不可解除合约; (4)签约用户根据合约执行过程中车辆放电调控比例获得相应的放电奖励。 2.3.2 合约B (1)与合约A中的第1条相同; (2)为满足用户的用车需求,规定合约执行过程中允许用户解约。设用户返程时刻为s3,解约时刻e3。为了平衡电网侧的合约执行度和用户的解约意愿,用户解约需要满足以下条件: 1)在用户较少社区负荷序列,有解约需求的用户在解约时刻,需经过当前社区负荷序列预测负荷γ的临近尖峰负荷出现时刻I; 2)若社区负荷序列用户数较多,则当解约用户车辆签订合约后合约最短连续执行时间t1不小于当前EV序列合约实行前的单台EV最长充电时间T时,有解约需求的用户方可解约; 3)解约仅对车辆有效,用户家庭合约执行效度不受影响。若用户已解约,则对应家庭合约由该社区负荷序列剩余车辆代为执行; (3)用户解除合约前所获得放电奖励由社区负荷序列内所有用户根据放电量比例分配;若有用户解约,则放电奖励由未解约用户分配,这也是放电奖励的分摊规则。 在策略执行过程中,规定EV不向电网反向供电,EV的放电功率直接由社区负荷序列消纳。基于弹性优化机制的社区负荷EV分群优化策略示意图如图5所示。 图5 基于弹性优化机制的社区负荷EV分群优化策略 根据上述优化策略,优化机制的实现流程如图6所示。 图6 策略流程图 本文分别以最小化负荷方差和用户支出总费用最小为目标来构建多目标优化函数。最小化负荷方差函数为 (3) 式中,P(i)和P(j)分别为社区在第i时刻和第j时刻的净负荷功;T为时间节点数;s和e分别为优化起止时间。 最小化费用函数为 (4) 式中,pbuy(t)为t时刻电网交换功率,包括家庭负荷和EV充电负荷;ipdis(t)为EV在t时刻的放电功率;Csell(t)和Cbuy(t)分别为t时刻的放电和购电价格。 当社区负荷序列的EV数量较多时,各EV之间应相互协调充放电行为。本文将同社区负荷序列签约用户的车辆视为整体,EV整体最大充、放电功率不得超过单台EV电池最大充、放电限度总和,且初始放电量不得超过初始时刻电池剩余电量,即 (5) (6) (7) 式中,N为当前社区负荷序列的车辆数;Npcha(t)和Npdis(t)为EV整体在t时刻充、放电功率;ipcha·max(t)和ipdis·max(t)为第i辆EV输出功率上限;ipdis·ini和ipori分别为第i辆EV初始放电量与初始可用电量。 考虑到EV电池的容量限制,规定EV的最大充电量为合约实行前EV剩余可充电量,即 (8) 式中,ηi为充电站的充电效率;Ei为第i辆EV的可用容量;ipcha(t)为第i辆EV在t时刻的充电功率。 若社区负荷序列存在用户解约的情况,则t时刻解约后的EV电池额定容量为未解约用户车辆的额定容量总和 (9) 式中,Erest(t)和iEori(t)分别为t时刻EV整体电池总容量及第i辆EV电池额定容量;M为未解约用户数,且M 为了延长电池使用寿命,剩余EV的电池的荷电量应保证在合理的范围内 (10) 式中,iSOCmin(t)和iSOCmax(t)为第i辆EV电池最小、最大荷电量;SOCt为EV整体平均荷电量值。相关的调查和统计结果表明[17],家庭EV保留30%的剩余电量即可满足出行需求,因此本文将iSOCmin设为0.3。同时,为防止电池过充,本文将iSOCmax(t)设为0.95。若初始时刻SOC(t)小于0.3,大于t时刻的SOC值应处于式(10)的范围内。 单台EV电池剩余电量计算式如下 (11) 式中,iSOC(t)为第i辆EV在t时刻的SOC值;iηcha、iηdis和Δt分别为第i辆EV的充电效率、放电效率和单位时间间隔。 当存在用户解约情况时,解约时刻剩余车辆平均SOC(t)为 (12) 式中,kSOC(t)为第k辆EV解约时在t时刻的SOC值;kpcha(t)和kpdis(t)为第k辆EV解约时在t时刻的充放电功率;kηcha和kηdis为第k辆解约的EV充放电效率。 EV电池充放电需要保持互斥性原则,即 Sdis+Scha+Sstatic=1 (13) Sdis,Scha,Sstatic∈{0,1} (14) 式中,Sdis、Scha、Sstatic表示放电状态、充电状态和电池静置状态,且属于0-1变量。 当用户参与合约,电网侧应当提供该用户家庭用电需求,如式(15)所示。 (15) 当用户签订合约并在执行过程中,EV应与电网协调平衡社区负荷序列的功率需求 (16) 式中,s、e为电网侧供电起止时间;ipbuy(t)为社区负荷序列各家庭交换功率;ipLoad(t)为t时刻社区负荷序列各家庭负荷。 电网交换功率不应该超过母线最大传输功率 (17) 式中,pnet·max(t)为t时刻母线最大传输功率。 面对大规模车辆充电需求预测问题,采用一般的方法较难解决,但采用Monte Carlo法可通过对车辆出行特性概率模型进行分析,建立出行特性和充电负荷需求的联系,在一定程度上能够满足充电负荷的预测要求。采用Monte Carlo法的预测流程如图7所示。 图7 基于Monte Carlo法的充电负荷需求预测流程 本文以某地社区114户家庭典型夏季负荷为算例来验证本文策略,共设置3个合约场景,其中场景1~场景3分别对应合约A执行场景、合约B执行场景及合约A和B联合执行场景,并通过MATLAB 2020a在Yalmip平台上调用Gurobi 9.1.1对模型求解。本文EV型号引用文献[18],车辆参数如表1所示。 表1 某品牌EV参数 本文购电电价采用文献[7]提供的夏季电价,并假设EV充、放电价格相同。电价如表2所示。 表2 购电价格 本文的仿真参数设定为:e1=7,e2=e3=24,m=M/N=0.7,iηcha和iηdis均为0.9,Δt为1 h。 5.2.1 合约场景1仿真结果分析 合约场景1的仿真结果如图8所示。在该合约场景中,不签约的用户不参与V2G放电,但电网侧需要满足该部分车辆的充电需求。在EV充电量相同的情况下,图8所示的社区负荷序列综合负荷曲线表明,在合约场景1实行前,在EV无序充电负荷的影响下,社区基础负荷叠加EV无序充电负荷使社区总负荷峰值达到5 500 kW,峰谷差率达67.19%。合约场景1实行后,在当日12∶00之前,由于返程车辆较少,用户合约执行效果不明显,使得社区负荷转移量较少;当日12∶00后,随着返程车辆的增加,合约执行效果显著提升,社区负荷量有明显降低,当日社区负荷峰谷差率降至63.45%;负荷在20∶00峰值转移量最大,为1 088.8 kW,单日平均每小时转移负荷约105.916 5 kW,整体峰谷差转移率为3.74%,说明执行本文提出的策略后可有效平滑负荷曲线,降低了尖峰负荷量。 图8 合约场景1实行前后社区负荷 除了负荷峰谷差有所改善,本文对合约场景1实行前后的费用支出情况也进行了分析。表3显示,合约场景1实行后,当日社区各负荷序列用户费用支出率平均降低约10.80%,通过EV放电所得收益使得用户总体节省约10 730.5元的费用,平均每户节省约49.55元。 表3 合约场景1实行前后用户费用 5.2.2 合约场景2仿真结果分析 合约场景2仿真结果如图9所示。在EV具有相同充电量的前提下,在合约场景2实行前,社区基础负荷叠加EV无序充电负荷其负荷峰谷差率达到67.19%;合约场景2实行后,当日10∶00后小区负荷水平有明显的下降,并于当晚的20∶00负荷转移量达到最大,为1 115.5 kW,负荷峰谷差率为64.31%,峰谷差较合约实行前降低约2.87%,平均每小时负荷转移量为108.400 5 kW,有效降低了社区负荷水平。 图9 合约场景2实行前后社区负荷 在负荷峰谷差改善的同时,用户的支出费用也有所降低。合约场景2实行前后费用支出情况如表4所示。 表4 合约场景2实行前后用户费用 合约场景2实行后,社区各序列用户费用率平均降低约5.23%,用户费用总支出减少约13 957.72元,平均减少约55.05元,用电费用有所降低。 5.2.3 合约场景3仿真结果分析 面对社区用户用车需求的不同,用户合约的签订也将有所差异。实际情况中,在合约可供用户选择时,文中两种合约发挥不同的效度。同时实行两种合约不仅可有效增加策略的弹性限度,适应不同需求的用户,还将有助于提升用户的响应度。在合约场景3中,假设合约签约率m仍为0.7且合约A与合约B的签约用户分别占签约用户总数的50%,用户根据自身的需求选择不同的合约。图10表明,在EV充电量一定的情况下,在合约场景3实行前社区峰谷差率为67.19%,而合约场景3实行后,社区峰谷差降至62.15%,峰谷差率减小了约5.04%,并且在20∶00的峰值量转移最大,转移负荷量为1 029 kW,实现了负荷削峰的目的。 图10 合约场景3实行前后社区负荷曲线 在负荷波动得到有效改善的同时,通过实行合约场景3,用户的支出费用也得到明显的减少。较合约场景3实行前,合约实行后用户总支出费用降低12 766.1元,平均每户降低约112元,费用平均减少率为10.55%。 表5 合约场景3实行前后用户费用 本文提出了基于弹性优化机制的社区负荷EV分群优化策略,该策略包含具有一定弹性限度的合约A与合约B。合约A侧重考虑用户收益,合约B侧重考虑用户用车需求。通过分群管控社区EV,并根据用户意愿与用户签订合约,以EV策略响应车群为调度载体,联合电网侧来优化各社区负荷序列,从局部降低社区整体负荷峰谷差。对3种不同合约场景实行后的结果分析表明,本文提出的策略能够在平滑社区负荷曲线的同时降低用户费用,提高了电网的可靠性和EV的可用度。
2.4 策略执行流程

3 目标函数及运行约束
3.1 目标函数
3.2 EV运行约束
3.3 功率平衡约束
4 基于Monte Carlo的充电负荷需求预测
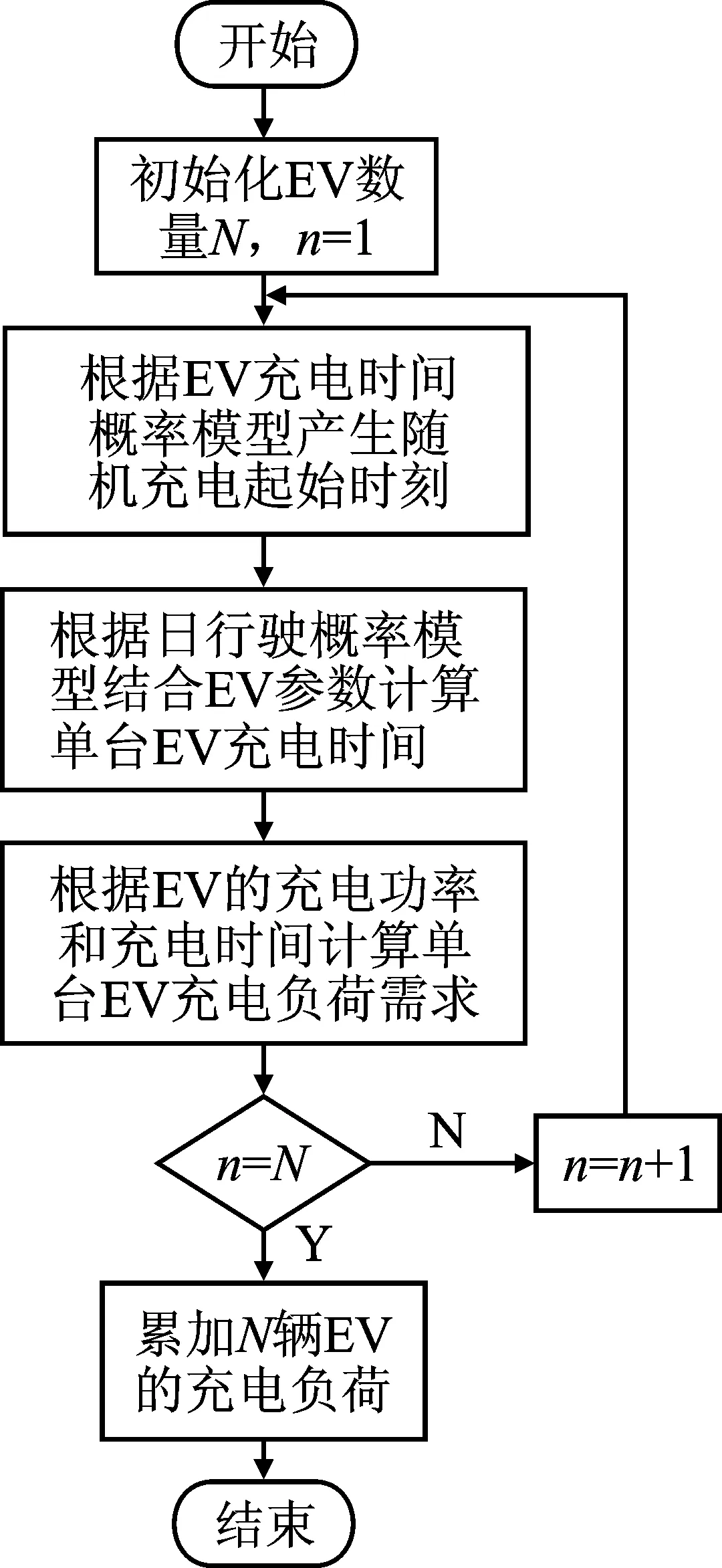
5 算例验证
5.1 算例背景


5.2 算例结果分析






6 结束语

