基于BIM技术的装配式建筑全寿命周期成本预测

相文强，池小兰

(福建林业职业技术学院 交通工程系，福建 南平 353000)

保护环境、节约资源是我国基本国策，绿色发展、生态文明已经成为我们的发展目标，装配式建筑能打造更美好的民居环境，提供更舒适、更优质的绿色住宅，构建人与自然和谐共生的建筑产品[1]。作为降低资源消耗、保护环境的建筑方式，装配式建筑可以提升住宅品质与标准化程度，实现多种资源的节约，具备绿色、环保、节能的发展优势。最近几年，装配式建筑在国外部分国家和地区已经实现大面积普及，国内也开始飞速发展[2]，很多大型建筑企业与房地产开发商纷纷转型，形成了装配式建筑的新产业链。在装配式建筑的发展中，全寿命周期成本问题一直是研究热点，包括成本的管理与预测等。对于成本预测，国外由于建筑工业化进程较快，发展相对成熟，特别是二战后的重建需求，使建筑工业化获得了长足发展，各国也形成了独特的市场模式与技术体系，发展装配式建筑更加得心应手，因此对该问题的研究也更深入。对于其全寿命周期成本预测，现阶段已经出现了很多的优秀研究成果，例如文献[3]提出基于人工神经网络模型的建筑工程成本预测方法，该方法利用Matlab软件、人工神经网络模型，以工程项目的一系列与成本相关数据为基础，得到施工成本预测结果。文献[4]提出基于栈式降噪自动编码器的建筑工程施工成本预测方法。该方法通过分析建筑工程施工影响因素，并对其进行量化分析，以此结合栈式降噪自动编码器理论与神经网络搭建相关的成本预测模型，将数据输入至该模型中，得到精准的预测结果。文献[5]提出基于GA-BP神经网络的建筑工程造价预测方法。以收集的30组样本数据为例，结合工程实际情况建立基于GA-BP神经网络的建筑工程造价预测模型，将收集到的数据输入至该模型中，得到相关的建筑工程造价预测结果。

由于以上成本预测方法，在预测迭代次数为5～20次的范围内存在运行时间较长、相对误差较大的问题，因此在成本预测方法的研究中提出了一种基于建筑信息模型(Building Information Modeling，BIM)技术的成本预测方法，并通过实验对该方法进行应用验证。

1 装配式建筑全寿命周期成本预测方法

1.1 成本分析

首先基于BIM技术对全寿命的装配式建筑进行成本分析，包括建设阶段成本、使用阶段成本。通过BIM技术实施建筑的全寿命虚拟建造，构建建筑BIM模型，在模型的周期构建过程中实施各阶段的成本分析。该过程中具体使用的技术包括BIM 5D 技术与大数据BIM管理技术。

建设阶段具体成本包括决策成本、设计成本、构件运输生产成本、安装施工成本、期间成本、税金、其他费用等，具体内容如表1所示。

表1 建设阶段具体成本内容

使用阶段具体成本包括物业管理、能耗以及维修工程设备成本[6]。

1.2 构建成本预测体系

选择能够对成本造成影响的指标，指标的选取具体从4个方面入手：装修装饰、安装施工、结构设计以及建筑特征，构建成本预测体系。

在装修装饰方面，装饰内墙时，可以减薄抹灰或直接免除抹灰，主要装饰种类包括乳胶漆、涂料、混合砂浆以及水泥漆类型的墙面[7]。装饰外墙时，不需要对保温层进行考虑，主要装饰种类包括玻璃幕墙、面砖、真石漆以及涂料类型的墙面。装饰楼地面时，与传统住宅没有太大差异，主要装饰种类包括细石混凝土、地砖、水磨石、水泥砂浆类型的地面[8]。采用的构件包括预制外墙与预制内墙构件，主要装饰内墙面、外墙面以及楼地面，因此选取这3方面作为装修装饰的指标。

在安装施工方面，根据现场施工情况选取成本预测指标。选取的4个指标包括项目管理水平、运输距离、工人专业化水平以及机械化施工水平[9]。

在结构设计方面，与之前相比增加了构件设计、二次图纸拆分等环节，因此设计成本有所增加，根据设计流程对成本预测指标进行选取[10]。所选取的指标具体包括施工深化设计、建筑结构类型、装配方案以及预制率。

在建筑特征方面，根据建筑情况对成本预测指标进行选取[11]。所选取的指标具体包括地上层数、层高以及建筑面积。

基于选取的成本预测指标所构建的成本预测体系具体如表2所示。

表2 构建的成本预测体系

组合层次分析法与粗糙集理论确定成本预测体系中各指标的对应综合权重，确定权重的具体过程如图1所示[12]。

图1 确定权重的具体过程

1.3 构建成本预测模型

结合极限学习机与粒子群算法构建成本预测模型进行成本预测[13]。首先利用极限学习机构建模型网络，具体构建步骤如下：

1)确定网络输出输入节点：根据成本预测体系中的指标个数确定网络的输入维度和节点数，而输出节点数则定为1[14]。

2)确定隐藏节点个数：通过选择激励函数确定具体个数。选择激励函数能够为极限学习机带来更强的线性建模能力，只有选择合适的极限学习机，才能获取理想的预测结果[15]。可选择的激励函数的描述及形式具体如表3所示。

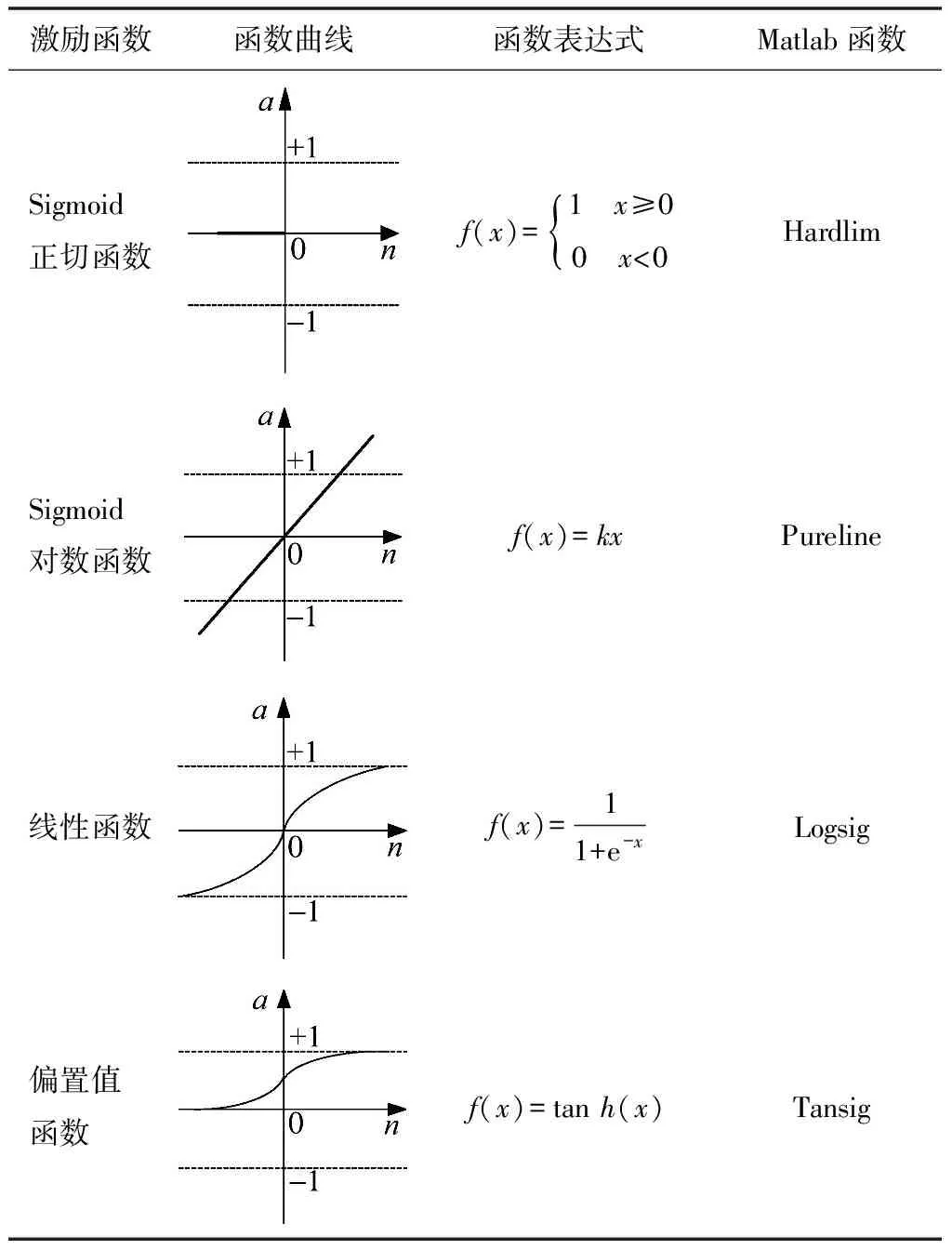
表3 可选择的激励函数的描述及形式

接着通过粒子群算法优化网络模型，优化时需要考虑以下方面：

1)隐藏层偏置值与输入权值

通过粒子群算法对隐藏层偏置值与输入权值进行优化，并将其作为粒子群算法里的粒子长度与粒子，具体如下式所示：

(1)

D=K(n+1)。

(2)

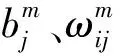
2)适应度函数

适应度是粒子位置好坏的评价测度，能够对极限学习机的实际泛化性能进行刻画。通过隐藏层偏置值与输入权值能够对输出权值矩阵进行求取，从而获取预测值[17]。对预测值来说，用均方误差来判断其精度能否满足要求：

(3)

通过优化网络模型实施成本全寿命预测，具体预测步骤如图2所示。

图2 具体预测步骤

2 案例分析

2.1 项目概况

实验中的装配式建筑为某学生公寓，该公寓的建筑结构为框剪装配结构，项目承包模式为工程总承包，整体建筑面积25 000 m2，分为2栋，其中A栋建筑地上楼层数为7层，地下楼层数为2层，总面积4 200 m2；B建筑地上楼层数为18层，地下楼层数为2层，总面积20 800 m2。该工程项目以清单方式计价，除了合同允许所做出的调整、各种奖罚、经济签证、设计变更、设备与材料的厂家或品牌变更、商品砼及钢筋价格上的风险调整、设备与材料调整暂定价格调整以外，不因为费率变动、技术措施费、机械费、材料价格、人工费等原因做出调整。

实验建筑的设计拆分，如图3所示。

(a)外墙板拆分图

2.2 实验方法设计

利用基于BIM技术的装配式建筑全寿命周期成本预测方法对其实施成本预测实验。进行成本预测实验之前，首先对方法中的成本预测模型进行训练和仿真，确定模型最佳参数后开始实验。

在实验中获取该方法的运行时间与相对误差实验数据，用这2种参数对预测效果进行反映。其中相对误差的计算公式为：

(4)

式中：∂代表相对误差，其值绝对值越小，证明模型成本预测能力越强。将文献[3]方法、文献[4]方法作为实验对比方法，以此验证不同方法的实际应用效果为增强结果的对比性。

2.3 实验结果

2.3.1 运行时间实验结果

对文献[3]方法、文献[4]方法以及本文方法的模型运行时间进行实验测试，在成本预测中的运行时间实验数据，如表4所示。

表4 运行时间实验数据

表4的运行时间实验数据表明，相比文献[3]方法、文献[4]方法，在预测迭代次数为5～20次的范围内，本文方法无论是对A栋还是对B栋进行成本预测都花费了更少的时间，证明本文设计的成本预测方法模型运行时间短于其他方法。

2.3.2 相对误差实验结果

本文方法与文献[3]方法、文献[4]方法的装配式建筑全寿命周期成本预测相对误差实验结果，如表5所示。

根据表5的相对误差实验结果，本文方法的相对误差比文献[3]方法、文献[4]方法更小，证明本文方法具备更强的成本预测能力。

3 结束语

在对装配式建筑整体成本预测问题进行研究的过程中，提出了基于BIM技术的成本预测方法，并验证了该方法多方面的性能，对于取得的研究成果，由于在成本分析阶段不够细致，将会继续进行该问题的深入研究。