Morison 方程在进水塔动水压力计算中的应用

党康宁，刘云贺，陶 磊，张静宜，张 希

（1.陕西省引汉济渭工程建设有限公司，陕西 西安 710011； 2.西安理工大学，陕西 西安 710048；3.中陕核工业集团监理咨询有限公司，陕西 西安 710060）

进水塔是水利水电枢纽工程的重要组成部分，随着工程建设规模日益扩大，进水塔作为工程咽喉对枢纽抗震安全的影响更为突出［1］。 地震时动水压力对进水塔的影响不可忽略［2-4］。 采用塔体与水体动力耦合的数值方法求解动水压力无疑是最准确的，但数值耦合法通常非常复杂，计算工作量极大，不便于推广使用。

解析算法具有便于对问题机理理解和计算相对简单等特点。 目前解析算法主要分为解析法和半解析方法，其中解析法以基于势流体的辐射波浪法应用较多，而1950年美国加利福尼亚伯克利大学的Morison 等提出的著名Morison 动水压力公式［5］被称为是研究流固耦合问题最具代表性的成果，是一种半解析半理论方法。

深水桥墩与进水塔有着非常类似的状况：结构大部分浸没于水中，底部嵌于地基之中，一般为实心或空心圆柱、椭圆柱，也有截面为矩形的桥墩，并且高度都很大，近年来，有众多研究者采用Morison 解析方法对深水桥墩进行了动水压力方面的研究［6-9］，取得较多成果。 因此，对于与桥墩形状和边界类似的进水塔结构，在一定假设基础上可通过解析算法进行定性分析，这在初步设计阶段对结构分析、调整极为有益。

本文尝试将Morison 方程用于内外均有水的矩形截面进水塔结构动水压力计算，通过对Morison 方程进行扩展，得到进水塔内部和外部的附加质量。 对比本文方法、附加质量公式和流固耦合求解得到的动水压力分布情况，并进行了适用性评价。

1 Morison 方程原理

Morison 方程主要用于求解与波长相比尺寸较小的细长柱体的波浪力，是以绕流理论为基础的半理论半经验公式。 该理论假定柱体的存在对波浪运动无显著影响，认为波浪对柱体的作用主要是黏滞效应和附加质量效应。

对于直径为d的细长圆柱，其表达式为［10］

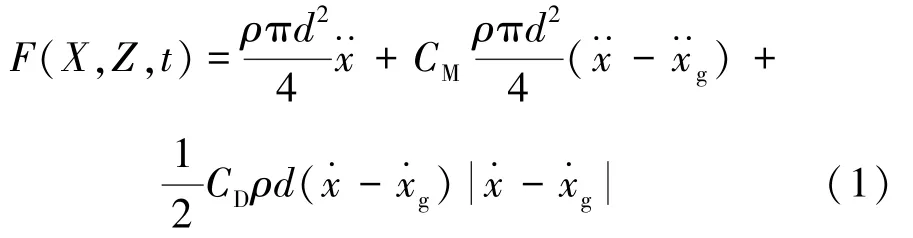
式中：F为波浪力；X为波浪水平运动方向坐标；Z为柱体高度方向坐标分别为结构运动速度、地面运动速度、结构运动加速度和地面运动加速度；CM、CD分别为等效惯性力系数、阻尼力系数；ρ为水体密度；t为时间。

对于矩形柱体地震动水压力的解答，需要将附加质量按截面等效关系进行修正，修正后的CM公式为［10］

式中：D为垂直于运动方向的柱体宽度；B为平行于运动方向的柱体宽度。

通过计算得到常见矩形墩的附加质量修正系数，见表1。

2 基于Morison 方程的进水塔附加质量计算

对于进水塔需要同时考虑塔内、塔外水体的动水压力影响（见图1），因此需要对Morison 方程进行扩展。

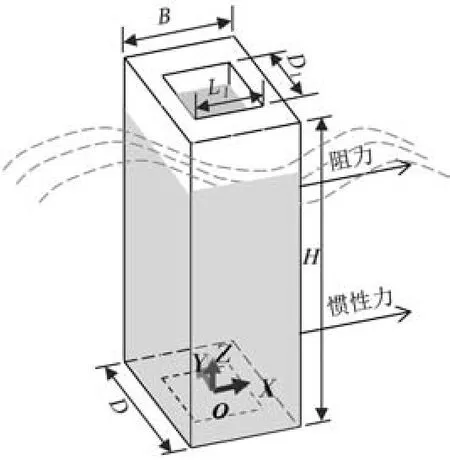
图1 波浪作用下进水塔受波浪力示意

假设塔体内部水体质点i速度为、加速度为，进水塔迎水面宽度为D、高度为H，根据Morison 方程原理，动水压力由两部分组成，即惯性力部分和阻尼力部分。 其中，阻尼力部分FD表达式为

惯性力由流体部分产生的惯性力F11和进水塔引起的惯性力F12两部分组成，分别为

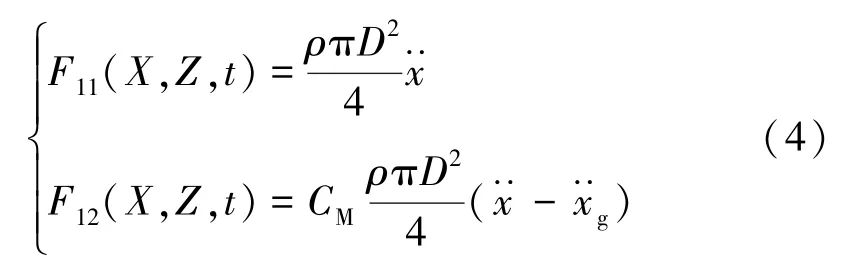
进水塔内部空腔尺寸一般小于10 m，仍可用Morison 方程推导。 在地震作用时，可认为塔内水体与外部水体独立，形成一个封闭水域，随着进水塔一起运动。 此时，塔内水体附加惯性力F11i为

式中：D1、L1为进水塔腔内迎水面和顺水面宽度。

于是，进水塔的Morison 方程可表示为

其中CD＝2。

进水塔处于库水中，可认为水体静止，进水塔对库水影响可以忽略，塔外和塔内水体加速度均为0，式（6）可变为

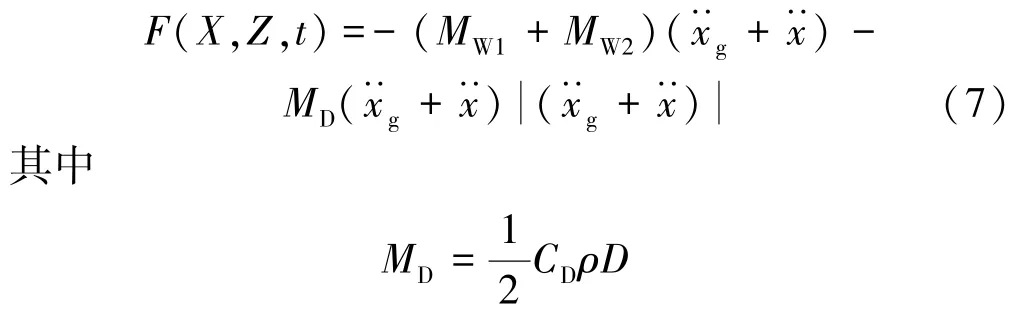
式中：MW1、MW2分别为进水塔外、塔内附加质量，MW1＝

研究表明，Morison 方程中非线性阻尼项对结构影响很小，为简化计算，一般可忽略［11］。 于是，式（7）简化为

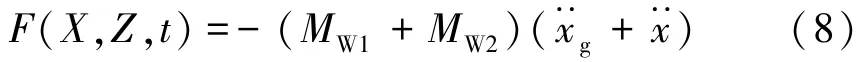
无水进水塔结构在地震作用下的微分方程为

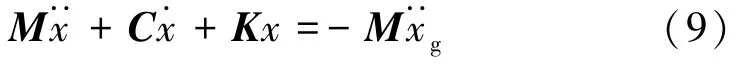
式中：M、C、K分别为质量矩阵、阻尼矩阵和刚度矩阵。

在进水塔内外有水时：

可采用有限元法进行求解，将塔内外水的附加质量添加进质量矩阵，进而得到进水塔的地震响应。

3 附加质量比较

水工抗震标准［2］中进水塔附加质量法处理方式与上述方法大致相同，仅计算附加质量的公式有区别。为分析本文方法求附加质量的可行性，以某实际工程进水塔为例，分别采用水工抗震标准进水塔附加质量法和本文方法计算进水塔附加质量。 进水塔各特征参数如下：进水塔高度81 m，塔体横截面内部尺寸4.68 m×7.00 m、外部尺寸13.56 m×14.00 m；塔体材料弹性模量28 GPa，塔体密度 2 500 kg／m3。 塔内外水深相同，均为75 m，水的密度为1 000 kg／m3。

图2 为本文方法和进水塔附加质量法求得的附加质量。

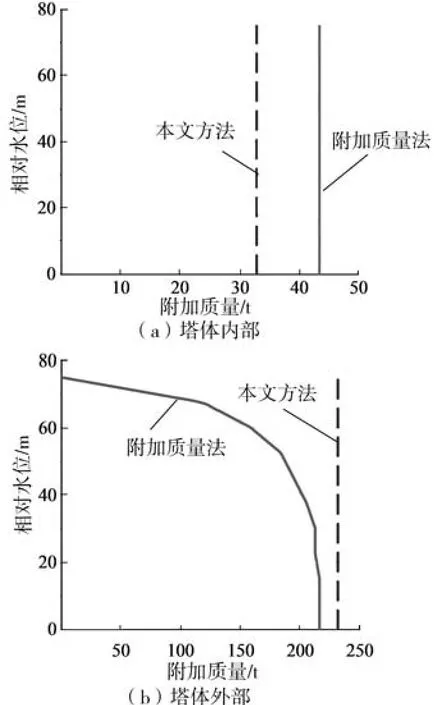
图2 两种方法附加质量比较

由图2 可知：对于塔体内部，相对水位变化时本文方法和附加质量法求得的附加质量都不变，但本文方法所得的值较附加质量法的小；对于塔体外部，本文方法所得的附加质量与附加质量法在40 m 以下相对水位对应的值较为接近。

4 动水压力计算分析

进水塔模型尺寸和材料参数与前节相同，建立有限元模型，分别采用本文方法、附加质量法与流固耦合方法对动水压力进行计算，以便对比分析。

无水的孤塔模型见图3（a），进水塔塔体采用三维实体单元，分别使用水工抗震标准中进水塔附加质量公式和Morison 方程附加质量公式计算节点质量，通过在塔体内外水面以下节点上添加质量单元实现。

进水塔和水体耦合模型见图3（b），进水塔塔体采用三维实体单元，水体采用三维势流体单元，水的体积弹性模量取2.1 GPa，进水塔四侧水体模拟范围为1 倍塔高。 进水塔底部完全固结，塔内外水体表面均设为不考虑重力作用的自由表面。

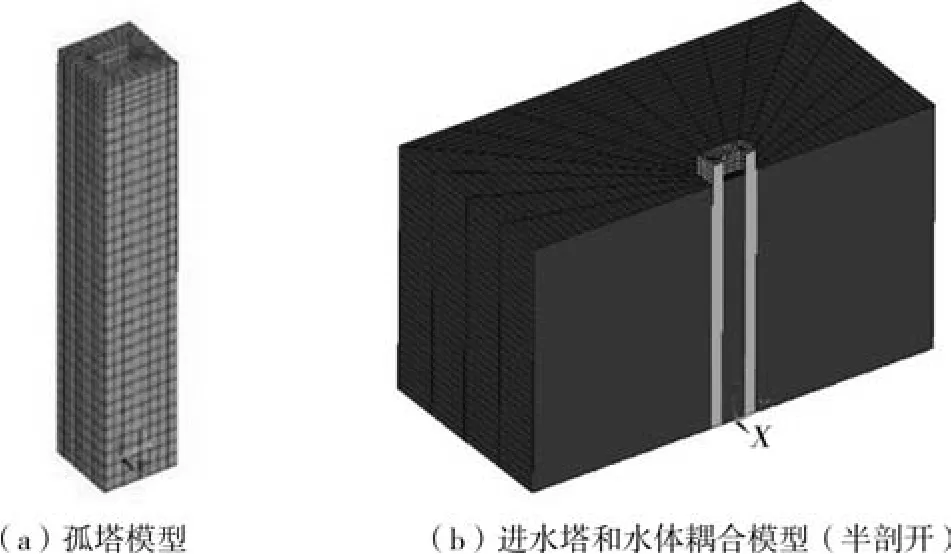
图3 进水塔有限元模型

对模型施加顺流向（有限元模型中X方向）地震荷载进行时程分析。 对于孤塔模型，提取进水塔高度方向的绝对加速度分布，进而可以根据节点所附加的质量和分摊面积求得动水压力曲线。 对于流固耦合模型，提取进水塔沿着高度方向的动水压力包络值，得到动水压力曲线。

附加质量法、Morison 方程和流固耦合方法动水压力曲线见图4。

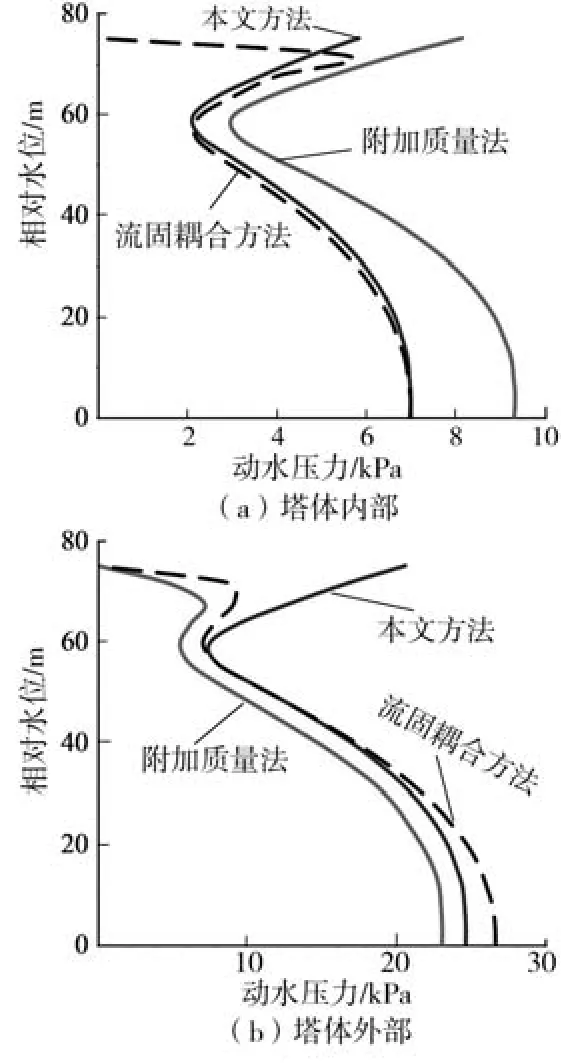
图4 3 种方法动水压力曲线比较

由图4 可知：在相对水位0 ～60 m 范围内，本文方法结果与流固耦合方法的非常接近，但由于Morison方程计算的附加质量与相对水位没有关系，因此在相对水位大于60 m 时动水压力呈现增大趋势，这与实际不符；附加质量法得到的塔体内部动水压力变化趋势与本文方法的相似，值整体大于本文方法的；附加质量法计算的塔体外部动水压力变化趋势与流固耦合方法的相似，但值略小于流固耦合方法的；在一定相对水位范围内本文方法计算结果与流固耦合方法的比较接近。

5 结 论

将求解水中细长柔性柱体的Morison 方程进行扩展，得到计算矩形截面进水塔内部和外部附加质量的公式。 推导过程表明，附加质量与塔体截面形状有直接关系，与相对水位无关。 动水压力计算分析表明，在一定范围内本文方法计算结果与流固耦合方法的比较接近，本文方法公式简单，计算简便，当仅需简单考虑进水塔动水压力作用时，本文扩展的进水塔Morison方程可为进水塔动力响应分析提供一种新思路。