全自动验光仪靶环中心定位算法研究

廉治文，刘 祎，张 权,

(1. 中北大学 信息与通信工程学院，山西 太原030051；2. 中北大学 生物医学成像与影像大数据山西省重点实验室，山西 太原 030051)

0 引 言

眼睛的健康问题被认为是人类生存质量的三大问题之一. 验光仪是通过检测眼睛相关参数来进行精准配镜的重要仪器[1]. 基于嵌入式系统的全自动验光仪需准确定位采集的实时图像中的人眼靶环中心，处理器根据返回的中心坐标控制电机将人眼定位到显示屏幕中心. 准确性高的靶环中心定位算法对验光仪配镜具有十分重要的作用.

当前，随机样本一致算法( RANSAC)、霍夫变换(Hough)、随机霍夫变换等方法仍然是国内外常用的靶环圆中心检测方法. 其中，RANSAC是基于几何与随机性来寻找图像中的圆，RANSAC中随机抽样的目的是使所估计的圆模型尽可能包含更多的边缘点，许多研究者仍侧重于改进随机选取边缘点的策略或优化相关的圆模型，但这并不能规避效率低、鲁棒性较差的问题[2-3]. 传统Hough变换几乎不可能应用于实际，因为该方法的参数空间为三维，计算量大、占用大量的内存空间，导致检测速度慢、效率低. 有研究者在现有方法中加入图像边缘梯度信息，时间得到提升，但检测精度下降、鲁棒性降低、不适合实时检测[4]. 随机Hough目前面临着与RANSAC同样的问题，需要尽可能地拟合到较多的点，对边缘存在缺陷圆的检测的准确性无法保证，一些研究者将随机Hough与亚像素相结合以提高抗干扰性，解决了鲁棒性的问题，但对于时间的提升有限[5-6]. 通常以低成本单片机为处理器的验光仪所采集的靶环图像会存在眼睫毛遮挡或半闭眼等缺陷，因此，这类传统方法会出现漏检率较高，定位不准确等问题，难以满足全自动验光仪实时检测的需求[7-10].

针对靶环图像复杂度较低、靶环特征明显的特点，本文提出了一种适用于嵌入式硬件系统实时处理的全自动验光仪靶环中心定位算法.

1 靶环中心定位算法

依据靶环图像的特点，本文通过构造模板在整幅图像上进行匹配，依据匹配计算得到的相关系数来确定中心，处理器根据返回的中心坐标控制伺服电机移动来实现靶环中心的实时检测. 算法主要包括中心粗定位及中心坐标校正两个阶段，详细流程如图1 所示.

图1 整体算法流程图Fig.1 Algorithm flow chart

1.1 中心粗定位算法

算法首先基于构造模板进行匹配操作，得到靶环中心粗定位坐标，主要包括以下部分：

1) 模板构造. 依据靶环图像特点，选取特征清晰、大小为m×n且包含靶环下半圆弧的矩形作为模板，其中长为m，宽为n.同时考虑模板的普适性，本文根据采集到的靶环图像的特点最终构造了由两个大小不同模板构成的组合模板.对采集的实际靶环图像进行大量实验验证，可以得出模板T2为0.8倍的T1时效果最佳，由此确定组合模板为{T1，T2}.在匹配运算过程中，依据计算结果自适应选择模板T1或T2.

2) 图像预处理. 由于靶环图像较大，为了降低运算量，提高算法实时性，根据靶环图像的特点对其进行隔行隔列采样. 同时，为了在不影响靶环边缘信息的情况下降低噪声的影响，使用中值滤波进行平滑处理.

3) 匹配运算. 在匹配运算时，首先选择模板T1，以图像左上点为起点，计算其与滑动过程中对应的图像块Iblock的相关系数R(x,y)，并以步长1进行滑动，遍历整幅靶环图像. 在匹配过程中，为了消除数据特征之间差异性的影响，采用基于模板与对应图像块内积运算的归一化匹配法匹配相关系数，定义为[11-14]

cosα=R(x,y)=

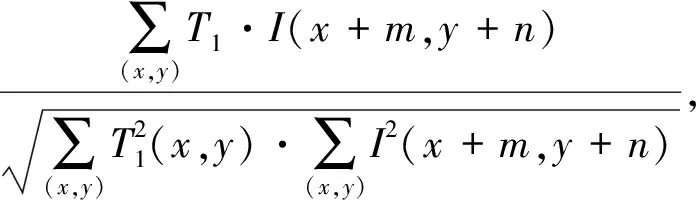
(1)

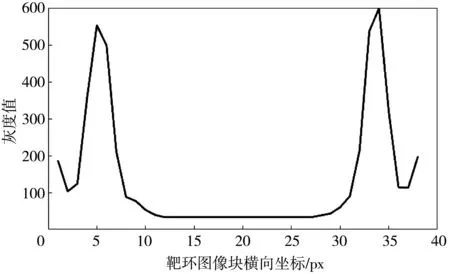
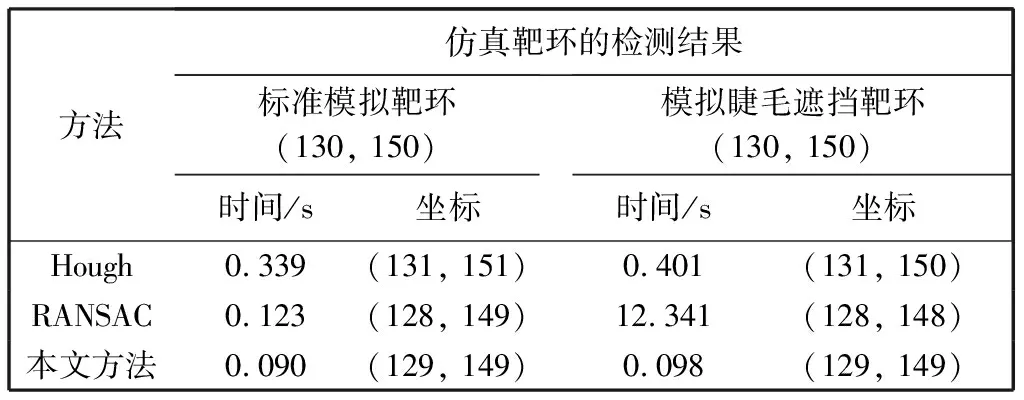
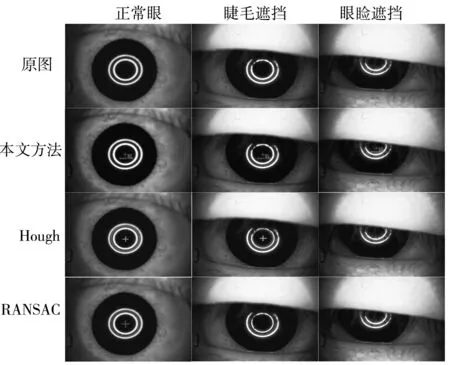
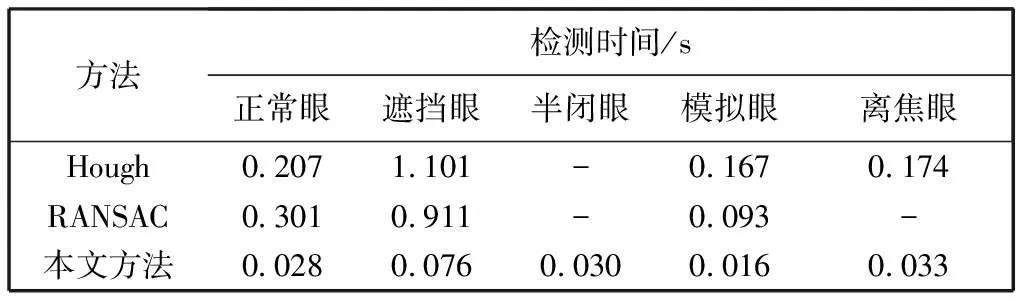
式中：0

4) 中心粗定位.匹配运算遍历完整幅图像后，在得到的相关系数曲面图中确定最大峰值，并进行阈值判断：若峰值小于设定阈值，则选取另一个模板T2重复步骤3)，进行二次匹配运算；否则，匹配运算完成，得到靶环中心的粗定位结果，并记录相关系数最大峰值在原图像中的坐标为(x,y)，以便进行后续校正计算. 对于阈值的设定要根据实际情况来确定，由于全自动验光仪各项参数基本确定，人眼靶环的大小不会有较大偏差，本文通过对所采集的各种情况的靶环图像进行验证，选取合适的阈值进行判定.

1.2 中心坐标校正算法

为了提高定位的准确性，对粗定位结果进行校正：以C(x,y)为左上像素坐标，在原图中截取一靶环图像块，如图2 所示. 由图可知，靶环图像具有内部灰度值较低、边缘亮环明显的特点，故采用投影法来确定靶环边缘位置，从而进行中心坐标校正. 算法主要包括投影、投影特征波峰识别及校正结果计算.

图2 靶环图像块Fig.2 Image of target ring

1) 投影运算. 对图2靶环图像进行垂直方向灰度值投影，并进行平滑处理后，得到如图3 所示的投影曲线. 由图可见，靶环边缘位置处特征明显.

2) 特征波峰识别. 针对图像靶环识别特点，在比较识别最大值法[10]的基础上进行改进，以识别图3中对应靶环位置的两个最大波峰：

以F=[f1,f2,f3...,fn]表示图3 投影.对F进行差分运算，得到

D′=fi+1-fi.

(2)

采用符号函数将D′归一为-1, 0, 1. 本文使用符号函数将差分的具体幅值归一到-1, 0, 1. 为避免比较法对一些数据可能失效的问题，直接把归一化后为0的值置为前一个非0值，即

(3)

在此基础上，最终对D进行二次差分，值为-2处即为波峰位置，而值为2处则为波谷位置，从而确定目标波峰的位置，即靶环左右边界的位置信息.

图3 矩形灰度值投影Fig.3 Rectangular gray value projection

3) 校正结果计算. 基于式(2)确定的靶环边缘左右位置分别为LEdge、REdge，则(REdge-LEdge)/2为靶环图像中心的横向坐标，在整幅图像中的横向坐标为x0=x+(REdge-LEdge)/2；然后，以x0为中心纵向取长度为m的目标区域进行水平方向灰度值投影，并进行与计算靶环坐标x0类似的处理，确定靶环边缘上下信息分别为TEdge、DEdge，从而得到靶环纵向中心坐标y0=y+(TEdge-DEdge)/2.校正后的中心坐标为 (x0,y0).

2 实验结果与分析

实验中，分别用传统Hough、RANSAC及本文算法进行中心检测. 在Windows平台中应用MATLAB 2017b进行算法研究，而实际应用中将代码翻译成C语言以适应嵌入式平台，转换为C语言的算法在嵌入式单片机中占据的空间大小只有10 KB，极易移植与部署使用. 检测图像选用验光仪实际采集的真实人眼、模拟人眼图像以及构造的已知中心的模拟靶环图像.

为了验证本文算法检测结果的准确性，构造了已知中心的仿真靶环(包括无睫毛遮挡、有睫毛遮挡)，靶环中心坐标为(130,150)，运用以上三种方法分别对已知中心位的仿真靶环图像进行检测，结果如图4 所示.

图4 制作的已知中心的靶环图像Fig.4 Produced image of known central target ring

2.1 仿真靶环中心检测结果及分析

由表1 的定量检测结果可知，对于无眼睫毛遮挡的仿真靶环图像，三种算法的准确性相当，而本文算法运算时间最短；而对于眼睫毛遮的图像，虽然检测的准确性均变化不大，但前两种算法，尤其是RANSAC的运算时间明显增加，而且由遮挡造成的部分信息缺失会使检测出现漏检的情况. 相比较而言，本文算法无漏检情况，稳定性好，同时在准确性、实时性方面也呈现出显著优势.

表1 仿真靶环的检测结果Tab.1 Test results of simulated target ring

2.2 模拟眼靶环与真实眼中心检测结果分析

综合分析图5，图6 以及表2，可以看出本文算法的优越性. 总体上，Hough变换和RANSAC对存在信息缺失图像的检测不够稳定，对于半闭眼以及模拟离焦眼的检测会出现漏检情况[15-17]，图像质量的干扰会导致检测效率降低，而本文算法对有信息缺失图像的检测无漏检情况，且准确率较高.

图5 模拟眼靶环检测Fig.5 Simulated target ring detection

图6 真实人眼靶环检测Fig.6 Real human eye target ring detection

为了证明本文方法在运算时间上的优越性，对比三种方法的检测结果，如表3 所示，可以看出本文方法的运算时间明显短于Hough变换和RANSAC. 从上述实验可以看出，本文方法在准确性、实时性等方面有显著优势.

表2 模拟/真实人眼靶环中心检测的结果Tab.2 Detection results of target ring center of simulated and real human eye

表3 真实人眼靶环检测时间Tab.3 Detection time of target ring in real human eye

3 结 论

本文提出了一种适用于嵌入式系统的靶环中心定位算法. 该算法通过构造合适的模板在目标图像上移动模板进行匹配运算，对验光仪采集的靶环图像具有很好的检测效果，无漏检情况，而且稳定性强、准确性高、检测时间短. 通过对采集的各类靶环图像进行检测，实验结果表明，与传统的Hough变换和RANSAC方法相比较，本文方法可以有效避免眼睫毛和眼睑遮挡对定位的干扰，在鲁棒性方面有较大的优势，可以很好地适用于靶环复杂的情况. 同时，本文方法在嵌入式平台上的检测时间上有较大提升，可以达到30 ms/帧，中心定位误差为±5像素，相较于传统算法有较大的提升，可以很好地满足全自动验光仪的靶环中心实时定位需求.