近海污染大气对自由空间量子通信性能的影响
张秀再,周丽娟,董千恒,翟梦思
(1.南京信息工程大学江苏省大气环境与装备技术协同创新中心,南京 210044;2.南京信息工程大学电子与信息工程学院,南京 210044)
量子信息是计算机、信息科学与量子物理相结合而产生的新兴交叉学科,量子保密通信以信息安全为基础,已经成为世界各国实施高新技术战略竞争的焦点之一。量子通信技术通过对光子、电子和冷原子等微观粒子系统及其量子态进行精确的人工调控和观测,借助量子力学原理和卫星中转技术,以经典理论无法实现的方式传输信息,在国防安全、军事等领域有着巨大的应用前景。2008年,Villoresi等[1]将弱光脉冲发射到距地面1 485 km的低轨道卫星上,地面接收机成功接收到卫星上角反射器反射的光脉冲,验证了星地量子通信的可行性。2010年,Jin等[2]通过一种主动前馈技术,在自由空间实现了超过16 km量子隐形传态,并达到89%的平均保真度,为量子科学实验卫星进行大尺度理论基础检验提供了必要的理论条件,也加速了中国构建全球量子通信网的步伐。2012年,中国科学家实现了百公里级量子隐形传态的实验[3]。2016年,中国发射了“墨子号”量子卫星[4],为进一步拓展自由空间量子卫星通信距离提供了现实基础。2020年,Juan等[5]在一场围绕量子通信的试验中,以每秒2对光子的速度在两地之间建立起量子纠缠,该试验实现了在较低码速率的情况下产生密钥的目标,意味着“墨子号”实现了1 120 km无中继量子密钥分发。
自由空间是量子保密通信的重要应用场景之一,空间背景环境对量子态造成干扰,降低了通信系统的可靠性。高锟等[6]研究了不同降雨强度对星地量子链路传输质量及通信性能的影响,为光量子信号在雨天环境中的顺利传输提供了参考。聂敏等[7]基于气溶胶的Gras模型,研究了不同海面风速对量子链路性能参数的影响,为海面上空量子卫星星舰通信的研究奠定了基础。
地球上约有60%的人口居住在近海地区,随着工业化和城市化进程的加快,人为污染物的排放增加,污染了近海的大气环境,改变了近海大气气溶胶的光学特性。顾芳等[8]研究了外混合气溶胶吸湿性对其平均消光系数的影响。高琦等[9]研究并分析了京津冀气溶胶时空变化的特征及潜在来源。在近海地区进行量子通信时,大气湿度和各种污染大气气溶胶粒子会导致量子链路性能的衰减。然而,尚未有关于近海污染大气环境对星地量子通信信道性能影响的研究。因此,研究近海污染大气对自由空间量子通信性能的影响具有重要意义。鉴于此,考虑了近海地区大气湿度对气溶胶粒径和复折射率的影响,针对幅值阻尼噪声、比特翻转噪声及相位阻尼噪声,研究了自由空间量子保密通信的信道特性。
1 近海污染大气气溶胶的光学特性
煤烟粒子、海盐粒子和水溶性粒子是近海地区污染大气气溶胶的主要组成成分。其中,海盐粒子、水溶性粒子的粒子尺度和光学性质受空气湿度的影响较大。由全球气溶胶数据集(global aerosol data set, GADS)可知[10],海盐粒子在近海污染大气气溶胶中的变化范围为0~1%;水溶性粒子的变化范围为40%~100%;煤烟粒子的变化范围为0~60%。考虑到近海地区大气湿度对气溶胶粒径的影响,吸湿后近海污染大气气溶胶粒子的粒径D可表示为
(1)
式(1)中:H为近海地区大气环境的相对湿度;s为常系数,取s=1;D0为干燥气溶胶的粒径。
近海地区大气中的散射粒子是不同尺寸的粒子集合,将不同尺寸的近海污染大气气溶胶粒子线性叠加近似处理,叠加后仍可看作球状粒子,类似于等效球体[11]。气溶胶粒子群的光散射特性与粒子的谱分布函数密切相关,近海污染大气气溶胶的粒度谱分布函数为
(2)
式(2)中:DM为气溶胶粒子的几何平均粒径;σ0为几何标准偏差,取σ0=2.00;N为单位体积内近海污染大气气溶胶粒子的数量,即粒子浓度,个/cm3。
近海污染大气气溶胶等效均匀球形粒子的复折射率实部mre、虚部mie、大气相对湿度H和粒径比之间的关系如下[12]。
(3)
(4)
式中:下标r、i、e、0、w分别表示复折射率的实部、虚部、吸湿后的气溶胶粒子、干燥气溶胶粒子和水。
湿度影响下的近海污染大气气溶胶粒子在波长λ下的平均复折射率me可表示为
me=mre+mie
(5)
采用λ为0.55 μm的光信号作为研究波长,此波段光的透过率高达95%,且辐射以单次反射为主。近海城市地区干燥的污染气溶胶在同一波段下的复折射率为me=1.75+0.44i,与近海污染大气气溶胶粒子反应的水滴粒子复折射率为mw=1.333+i1.96×10-4[13]。根据式(1)~式(4),取干燥气溶胶粒径D0为0.1 μm,可计算出近海污染大气气溶胶粒子的粒径、等效折射率实部、等效折射率虚部与大气相对湿度的关系曲线如图1所示。可以看出,随着大气湿度的增大,近海污染大气气溶胶粒子的粒径随之增大,等效折射率实部、虚部均呈现下降趋势。当大气相对湿度H>80%时,近海污染大气气溶胶粒径急剧增大,而等效折射率实部、虚部变化较为平缓。当大气相对湿度为80%时,气溶胶粒径为0.5 μm,等效折射率实部mre=1.336,虚部mie=3.05×10-3。可见,大气湿度的变化使近海污染大气气溶胶的光学特性发生改变,从而改变了粒子的散射能力。

图1 大气相对湿度与近海污染大气气溶胶粒径、等效折射率实部、等效折射率虚部的关系曲线
2 近海污染大气对量子通信链路衰减的影响
在自由空间进行光量子信号传输时,近海污染大气气溶胶与光子之间相互碰撞,导致光子能量衰减,影响星地量子链路传输性能。由于大气湿度对气溶胶粒径D和复折射率me有一定的影响,根据Mie散射,吸湿后的粒子散射光球谐函数a′n和b′n可分别表示为
(6)
(7)
式中:尺度函数xe=2πD/λ;ψ′n(xe)、Z′n(xe)分别表示ψn(xe)和Zn(xe)关于xe求导;ψn(xe)和Zn(xe)为Riccati-Bessel函数,可分别表示为
(8)
(9)

近海污染大气气溶胶粒子的消光效率因子Qext可表示为
(10)
式(10)中:Re(·)表示取实部。
近海污染大气气溶胶粒子Mie散射的消光系数可表示为
(11)
当光量子信号在自由空间传输时,由近海污染大气气溶胶粒子所导致的能量衰减可表示为[14]
E=E0exp(-kextd)
(12)
式(12)中:E0为初始能量;d为传输距离,km;E为光信号传输后的能量。
对式(12)取对数运算,可得近海污染大气气溶胶的链路衰减系数Latt为
(13)
采用波长λ=0.55 μm的光信号进行量子通信,当大气相对湿度为80%时,用MATLAB仿真得到近海污染大气气溶胶粒子浓度与信号传输距离、链路衰减的关系如图2所示。可以看出,随着近海地区污染大气气溶胶粒子浓度和传输距离的增加,链路衰减系数呈上升趋势,且气溶胶粒子浓度越大,星地量子链路衰减愈发剧烈。当传输距离为10 km,粒子浓度为100 cm-3时,链路衰减系数达到最大值,为4.72 dB。在大气相对湿度为80%的环境下,当传输距离为1 km,近海污染大气气溶胶粒子浓度由20 cm-3增加至60 cm-3时,链路衰减由0.09 dB上升至0.38 dB。因此,在近海地区进行量子通信时,随着通信距离的增加,将会对通信链路造成极大的影响。为了避免链路衰减系数过大,应当根据大气湿度和近海污染大气气溶胶粒子的浓度适当调整通信系统的各项参量。

图2 链路衰减系数、近海污染大气气溶胶浓度与传输距离的关系
3 近海污染大气对量子通信链路效率的影响
星地高效率光链路的建立是进行自由空间量子通信科学实验的必要条件,根据量子叠加性原理,量子通信系统设有两个检测器。在近海地区进行量子通信时,探测器检测到光信号的最少计数Wmin和本底噪声计数Wacc可分别表示为
Wmin=vηlinkη1η2
(14)
Wacc=V1V2Δτ
(15)
式中:v为光子的实际产生速率,取v=5×105s-1;ηlink为链路效率;η1和η2为接收量子信号时所用检测器的检测效率,取η1=η2=30%;V1和V2为检测器的暗计数率,取V1=V2=103s-1;Δτ为两个检测器的定时分辨率,取Δτ=5×10-9s。为了使探测器能够将量子光信号从背景噪声中检测出来,检测器检测到光子的最少计数Wmin、本底噪声计数Wacc与信噪必须满足以下条件[15]。
(16)
式(16)中:SNR为信噪经。
在量子物理学中,非局域性是量子力学的基本性质,量子纠缠态最大地违背Bell不等式,SNR为5.89∶1[16]。结合式(14)~式(16),可得链路效率极值为
(17)
在近海地区进行量子通信时,受近海污染大气气溶胶粒子的影响,丢失一个光子的概率可表示为
p=1-exp(-kextd)
(18)
故光子的实际产生速率v可定义为
v=pv′
(19)
式(19)中:v′为光子产生速率典型值,取v′=5×105s-1。
结合式(11)、式(17)~式(19),近海地区大气相对湿度为80%的环境下,当最大传输距离为10 km时,量子链路效率与近海污染大气气溶胶浓度之间的关系如图3所示。可以看出,随着传输距离和近海污染大气气溶胶浓度的增加,星地量子链路效率呈下降趋势,最终趋于0。在大气相对湿度为80%的环境中,当传输距离为0.5 km,气溶胶浓度为5 cm-3时,量子链路效率上升到最大值,为2.41×10-4,大于链路效率极值10-6,通信质量较高。当传输距离大于3 km,近海污染大气气溶胶浓度高于30 cm-3时,星地量子链路效率低于7.02×10-6,且变化平稳。当传输距离大于9.5 km,近海污染大气气溶胶浓度高于95 cm-3时,星地量子链路效率极低,小于链路效率极值10-6,此时量子信道将不能传输量子信号。因此,较高的近海污染大气气溶胶浓度会造成量子链路效率降低,在近海地区进行通信时,应选择良好的大气环境,建立高效率的量子通信链路。
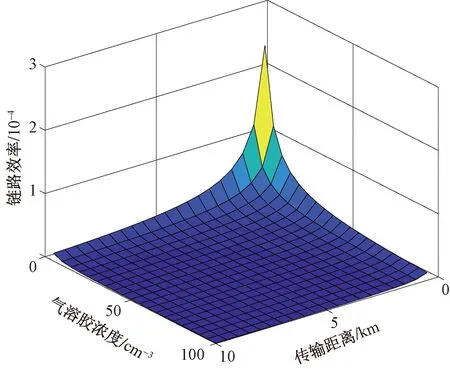
图3 量子链路效率、近海污染大气气溶胶浓度与传输距离之间的关系
4 近海污染大气对量子纠缠度的影响
量子隐形传态基于量子的纠缠特性,纠缠光信号在自由空间信道传送的过程中受到近海污染大气环境的影响,产生相互作用,引起量子态发生跃迁,导致量子纠缠信号纠缠度的下降。该过程可以等效为一个联合的幺正变换U,可表示为[17]
(20)
式(20)中:|0〉s、|1〉s分别为量子系统的基态、激发态;|0〉j、|1〉j为近海大气环境的计算基矢;p为受近海污染大气气溶胶影响,丢失一个光子的概率。
量子系统的复合量子比特纯态可表示为[18]
|ψ〉=r1|00〉s+r2|11〉s
(21)
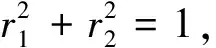
当近海污染大气环境量子态处于状态|0〉,幅值阻尼信道下复合系统的量子态可表示为

r1|00〉s|00〉j
(22)
式(22)中:|00〉j、|01〉j、|10〉j、|00〉s为近海污染大气环境中量子比特的不同状态;|00〉s、|01〉s、|10〉s、|11〉s为复合量子系统中量子比特的不同状态。
对式(22)求偏迹后得到纠缠系统的约化密度矩阵,可知幅值阻尼信道量子纠缠度为[19]
(23)
在大气相对湿度为80%的环境下,幅值阻尼信道量子纠缠度与近海污染大气气溶胶浓度、传输距离之间的关系如图4所示。可以看出,量子信道纠缠度随着传输距离和气溶胶浓度的增大呈下降趋势。当传输距离不变时,随着气溶胶浓度的降低,能量衰减增大,纠缠度呈下降趋势。当气溶胶粒子浓度为100 cm-3,传输距离为20 km时,振幅阻尼信道纠缠度下降到最小值,为0.013。在大气相对湿度为80%的环境下,当传输距离为1 km,近海污染大气气溶胶粒子浓度由20 cm-3增加至60 cm-3时,幅值阻尼信道量子纠缠度由0.96减小至0.88。

图4 量子纠缠度、近海污染大气气溶胶浓度与传输距离的关系
5 近海污染大气对量子隐形传态保真度的影响
5.1 近海污染大气环境对比特翻转噪声保真度的影响
保真度是描述有效量化目标状态和输出状态之间差异的一种度量方式,可用于评估量子隐形传态的传输质量。设有A、B两个量子系统,则A、B之间的保真度可表示为
(24)
式(24)中:ρA、ρB分别为A和B量子系统的密度矩阵;tr(·)表示求迹;当且仅当ρA=ρB时,保真度才为1。
对于用Bloch球面表达的单量子比特之间的保真度为[20]
F(θ,φ)=〈ψA|ρB|ψA〉
(25)
式(25)中:|ψA〉为量子系统A的状态向量形式;θ为相位因子;φ为极化因子。
量子态的平均保真度可表示为[21]
(26)
引入部分记忆信道后,噪声影响下的隐形传态平均保真度可表示为[22]
(27)
式(27)中:μ为量子隐形传态中一对粒子做相同旋转时的概率[23],0≤μ≤1;参数a1、a2、a3可分别表示为
(28)

引入比特翻转噪声后,量子态发生翻转,式(28)中的概率参数分别为p0=1-p、p1=p、p2=p3=0,其中,p为受近海污染大气气溶胶影响,丢失一个光子的概率。因此,在比特翻转噪声下,量子隐形传态平均保真度可表示为
(29)
由式(29)可知,当μ=0时,每个粒子独立通过比特翻转噪声信道,相应的平均保真度可表示为
(30)
当0<μ<1时,F1>F′1;当μ=1时,粒子完全关联,比特翻转噪声信道保真度为1。
结合式(18)、式(29),当大气相对湿度H为80%,传输距离为6 km时,仿真得到比特翻转噪声下,信道平均保真度与近海污染大气气溶胶浓度、参数μ之间的关系如图5所示。可以看出,在比特翻转噪声影响下,信道的隐形传态平均保真度随着参数μ的增大而增大,随着近海污染大气气溶胶浓度的增大而减小。当μ=0时,信道衰减为无记忆的噪声信道,量子隐形传态过程中粒子均独立受到噪声影响,信道保真度衰减到最小值;当μ=1时,粒子受到的噪声影响一致,此时不管近海污染大气气溶胶浓度如何变化,信道保真度均为1。当μ=0.5,近海污染大气气溶胶粒子浓度由30 cm-3上升到80 cm-3时,比特翻转噪声信道平均保真度由0.90衰减到0.84。因此,比特翻转信道的量子隐形传态平均保真度受近海污染大气环境的影响衰减较大,应根据实际环境调整系统的各项参量,提高自由空间量子通信的可靠性。

图5 比特翻转噪声信道平均保真度与近海污染大气气溶胶浓度、参数μ之间的关系
5.2 近海污染大气对相位阻尼噪声保真度的影响

(31)
式(31)中:σ为相位阻尼系数;ζ为近海污染大气环境的非均匀度;γ为自旋比特初始态角度;M为将时间t分为M个时间间隔。
设在相位阻尼信道中,初始量子态为
|φ〉=m|0〉+n|1〉
(32)

则量子态的初始密度矩阵为
(33)
量子态α|0〉+β|1〉经过相位阻尼噪声信道的演化过程为
(34)
式(34)中:|e〉为近海污染大气环境干扰下的等效量子态;pt为量子位与近海污染大气环境干扰等效量子态发生完全弹性散射的概率;I、X和Y为基本算子,分别表示为
(35)
式(35)中:j为虚数单位。
经过相位阻尼信道后,初始量子态密度矩阵演化为
(36)
式(36)中:ρ00、ρ01、ρ10、ρ11为量子态初始密度矩阵ρs的4个元素。
对于相位阻尼噪声信道,其保真度可表示为

(37)
令m2=f,n2=g,则相位阻尼噪声影响下,量子信道保真度可表示为
(38)
当大气相对湿度H=80%,M=2时,相位阻尼噪声影响下,信道保真度F2与参数f、量子位与近海污染大气环境干扰等效量子态发生完全弹性散射的概率pt之间的关系如图6所示。可以看出,在相位阻尼噪声下,量子信道保真度随着量子位与近海污染大气环境干扰等效量子态发生完全弹性散射的概率pt的增大而减小。当0 图6 相位阻尼噪声信道保真度F2与参数f、量子位与近海污染大气环境干扰等效量子态发生完全弹性散射的概率pt之间的关系 研究了近海污染大气对星地量子通信链路的影响。基于Mie散射理论,结合近海地区空气湿度对气溶胶粒径及复折射率的影响,计算了吸湿后粒子的粒度谱分布函数和消光系数。考虑到近海地区大气污染和空气湿度等条件,研究了3种噪声信道下的参数特性,建立了幅值阻尼噪声信道、比特翻转噪声信道以及相位阻尼噪声信道模型,得出如下结论。 (1)近海地区,大气湿度对气溶胶粒径及散射能力的影响较大。取干燥气溶胶粒径D0为0.1 μm,当大气相对湿度为80%时,近海污染大气气溶胶粒径为0.5 μm,等效折射率实部为mre=1.336,虚部为mie=3.05×10-3。 (2)近海污染大气相对湿度为80%的环境下,当传输距离为6 km,气溶胶粒子数浓度为60 cm-3时,链路衰减、链路效率、幅值阻尼信道量子纠缠度分别为1.7 dB、2.02×10-6、0.457。 (3)在比特翻转噪声下,近海污染大气湿度为80%,传输距离为6 km,量子隐形传态过程中参数μ=0.5,近海污染大气气溶胶粒子浓度为80 cm-3时,比特翻转噪声信道平均保真度为0.84。 (4)在相位阻尼噪声下,对于同一参数f而言,量子信道保真度随着量子位与近海污染大气环境干扰等效量子态发生完全弹性散射的概率pt的增大而减小。当pt=0.5,参数f由0.1上升到0.5时,信道保真度由0.93衰减到0.79。 可见,近海污染大气环境对自由空间量子通信的各项性能参数均有显著的影响,本文的仿真结果可为近海地区量子通信系统的设计与优化提供参考。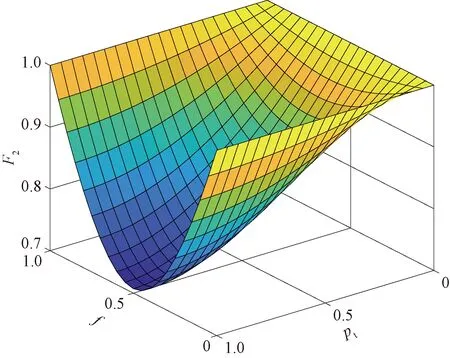
6 结论

