基于振动特性的铁塔螺栓完全松动检测方法

刘杰，王向东，贾伯岩，贾东亮，万书亭*

(1.国网河北省电力有限公司电力科学研究院，石家庄 050021；2.华北电力大学河北省电力机械装备健康维护与失效预防重点实验室，保定 071003)

螺栓作为输电铁塔塔材上重要连接件，在保证输电铁塔运行安全稳固上发挥着十分紧要的作用。由于输电铁塔常年经受强风影响，导致螺栓逐渐松动、输电铁塔刚度下降，严重影响输电铁塔正常运行。因此对螺栓的运行状况作出评估，并及时进行相应的维护势在必行。

中外学者做出了大量理论研究和实验来检测螺栓连接结构的松动故障[1]，其中主要有扭矩法、超声波检测、预紧力检测、振动信号检测、图像识别等离线和在线检测技术等。在超声波探测法的研究上，李鹏江[2]将超声波检测技术应用到气体绝缘组合电气设备(gas insulated switchgear, GIS)盆式绝缘子螺栓状态监测上，并成功实现了对螺栓松动的检测；吴冠男等[3]将混沌超声波激励应用到单肢螺栓连接结构松动的检测，并得到了螺栓松动的特征参量。虽然超声波探测技术有无损探测和分辨率高等特点，但其准确性有待提高。在预紧力检测法的研究上，江文强等[4]通过对螺栓在横向载荷下的预紧力的变化过程进行仿真，来判断螺栓松动的过程；张铁亮等[5]利用实验的方法对螺栓在横向振动载荷作用下的防松性能进行了定量评价。虽然预紧力检测法可以通过测量螺栓螺杆的轴向预紧力从而实现精准地对螺栓松动情况进行评价，但是由于这种方法需要对螺栓预紧力进行长期地监测，不适用于对螺栓松动快速检测。目前应用最为广泛的是根据螺栓松动前后振动信号的差异对螺栓松动进行检测和预测，何冰等[6]通过对输电铁塔施加外界激励，进而测得输电铁塔螺栓连接结构的振动信号，从振动幅值的区别上对螺栓松动进行评价；陈仁祥等[7]将基于振动敏感特征与流形学习的方法应用于风机基座螺栓松动程度诊断；Todd[8]利用螺栓松动前后振动模态参量的变化特征判断螺栓是否松动；屈文忠等[9]将亚谐波共振识别方法应用于螺栓损伤检测。在工程实际中，外界的干扰噪声严重影响了振动信号的采集，所以需要对振动信号做进一步地降噪处理。伍济钢等[10]将螺栓连接结构的平均振动能量应用于螺栓松动检测；闫航瑞等[11]将小波分析法应用到螺栓松动前后系统振动信号的处理中；周文强等[12]将经验模态分解(empirical mode decomposition, EMD)用于螺栓松动振动信号处理中，但EMD算法存在效率低下、模式混叠和端点效应等缺陷，因此往往会影响故障的识别，而变分模态分解(variational mode decomposition, VMD)相对于EMD可以很好地避免模态混叠与端点效应。

综上可知，针对输电铁塔螺栓完全松动故障缺陷，提出基于振动特性的铁塔螺栓完全松动快速检测方法，对输电铁塔螺栓连接完全松动前后在脉冲激振下相连接的两塔材振动响应进行试验分析，并利用自相关-VMD方法进行振动信号处理，最终通过对比螺栓完全松动前后的频谱图检测螺栓连接结构是否完全松动。

1 自相关-VMD降噪分解理论

1.1 自相关降噪

自相关是将信号不同时刻对应的数据做相关性分析的过程。利用自相关函数可以很好地找出时域信号上重复的模式，还可以识别出隐藏在信号谐波频率中的基频频率。因此自相关函数广泛应用于信号识别、提取有用信号和剔除噪声等信号处理上。自相关函数相关定义为

(1)

式(1)中：Rx(t)为自相关函数；T为积分周期；x(t)为信号函数；x(t+τ)为信号函数x(t)时移τ时刻后的函数。

1.2 VMD

变分模态分解是基于经典维纳滤波和Hilbert变换的一种自适应信号分解算法。VMD假设其分解之后的每个模态分量(intrinsic mode function, IMF)都是集中在各自中心频率附近的窄带信号。VMD分解需要3个步骤的处理方式：①对原信号Hilbert变换求解析信号；②将信号平移到基带；③对梯度的2范数的平方估计信号的带宽。上述变分约束的过程可由式(2)、式(3)进行描述。

(2)

(3)

式中：{uk(t)}={u1(t),u2(t),…,uK(t)}为各IMF分量；{ωk}={ω1,ω2,…,ωK}为各IMF分量的中心频率；δ(t)为脉冲函数；K为分解得到的模态数量；f(t)为待分解的原信号。

为求解上面构造的变分问题，可以引入拉格朗日乘子λ与二次罚因子α，引入增广拉格朗日函数，可表示为

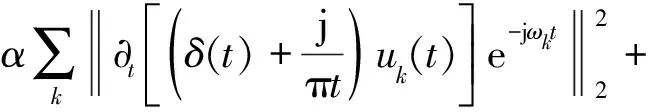
(4)

式(4)中：α为惩罚因子；λ(t)为拉格朗日乘子；L()表示进行拉格朗日运算；∂t()表示对t进行求偏导。

通过搜索可以得到每个IMF分量uk(ω)与其中心频率ωk的迭代方式如式(5)、式(6)所示。

(5)

(6)

拉格朗日算法的算子λ的迭代方式可表示为

(7)

不断地按照式(5)～式(7)进行迭代，当拉格朗日函数出现极小值点，迭代结束，这样原信号被最终分解为k个IMF分量uk(t)。

2 现场实验

2.1 实验系统搭建

为获得输电铁塔螺栓紧固和完全松动时振动产生的信号数据，就某电力公司的输电铁塔进行了现场实验，该输电铁塔为110 kV输电铁塔，修建完整，尚未投入使用。现场输电铁塔上所选的待测螺栓和振动测点如图1所示。

探究在保证激振位置不发生改变的条件下，螺栓完全松动故障测点位置对检测结果的影响。选择合适的测点对螺栓松动前后的振动数据进行采集，最终实验选定待测螺栓如图1所示，并在该螺栓所固定的两个塔材上分别选取两个测点进行研究。其中各测点与待测螺栓之间的详细位置如表1所示。

表1 各测点的详细位置

图1 输电铁塔待测螺栓和振动测点

考虑到输电铁塔的实际检测工况，激励源采用脉冲激励的方式，即利用脉冲力锤对输电铁塔施加脉冲激励。所选脉冲力锤的力传感器，灵敏度为4.44 pC/N，可以满足铁塔局部区域的激振和信号的采集；振动传感器采用压电加速度传感器，其轴向灵敏度分别为100.051 mV/g，利用磁吸座固定将其在输电铁塔的角钢上；选择合适的信号采集仪和PC端的信号处理仪器。最终，根据现场情况和选取的实验仪器完成最后的试验系统的搭建工作。最终，根据现场情况和选取的实验仪器完成最后的试验系统的搭建工作，如图2所示。

图2 输电铁塔螺栓检测实验系统

2.2 现场实验流程和实验可靠性验证

现场设定信号采集仪5 kHz的采样频率，分别进行两组不同的实验。

2.2.1 实验一

利用扭矩扳手将待测螺栓调节为完全紧固的状态，手持激振锤在激振点对输电铁塔塔材施加脉冲激励，利用振动加速度传感器和动态信号采集仪分别在4个测点对振动信号进行采集，最后利用PC端上的频谱分析软件对采集得到的信号进行信号处理。

2.2.2 实验二

利用扭矩扳手将待测螺栓调节为完全松动的状态，重复实验一的操作过程。

试验台的稳定性对避免实验的偶然性来说至关重要。为验证其稳定性，对每种状态下的螺栓进行10次实验分析，并求解了现场检测的10组数据之间的相关系数|r|如表2所示。

表2 数据间的相关系数

如表2所示，其统计的相关性数据可知，10组数据之间的相关系数|r|均在0.87以上，这表明前后10次试验数据重复性良好，输电铁塔螺栓完全松动分析测试信号稳定可靠。

3 实验数据处理和结果分析

3.1 基于自相关-VMD分解降噪法的输电铁塔振动信号降噪处理

在现场对输电铁塔螺栓连接松动故障检测时，由于外界各种干扰的存在，需要对采集得到的塔材振动信号做降噪处理。选择自相关-VMD分解降噪的方法对原始振动信号进行降噪处理。图3为自相关-VMD分解降噪法处理过程的流程图。首先利用自相关函数对振动传感器采集的信号进行降噪处理，以螺栓紧固时1测点的振动信号为例，其经自相关处理后的时域图如图4所示。

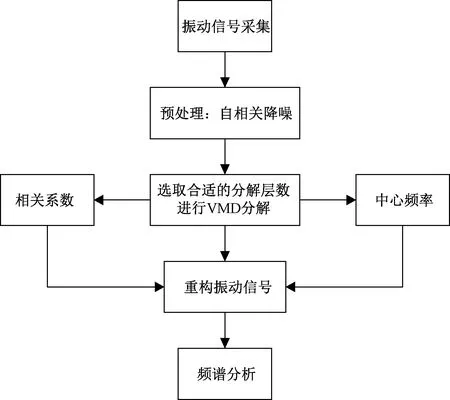
图3 自相关-VMD分解降噪法流程图

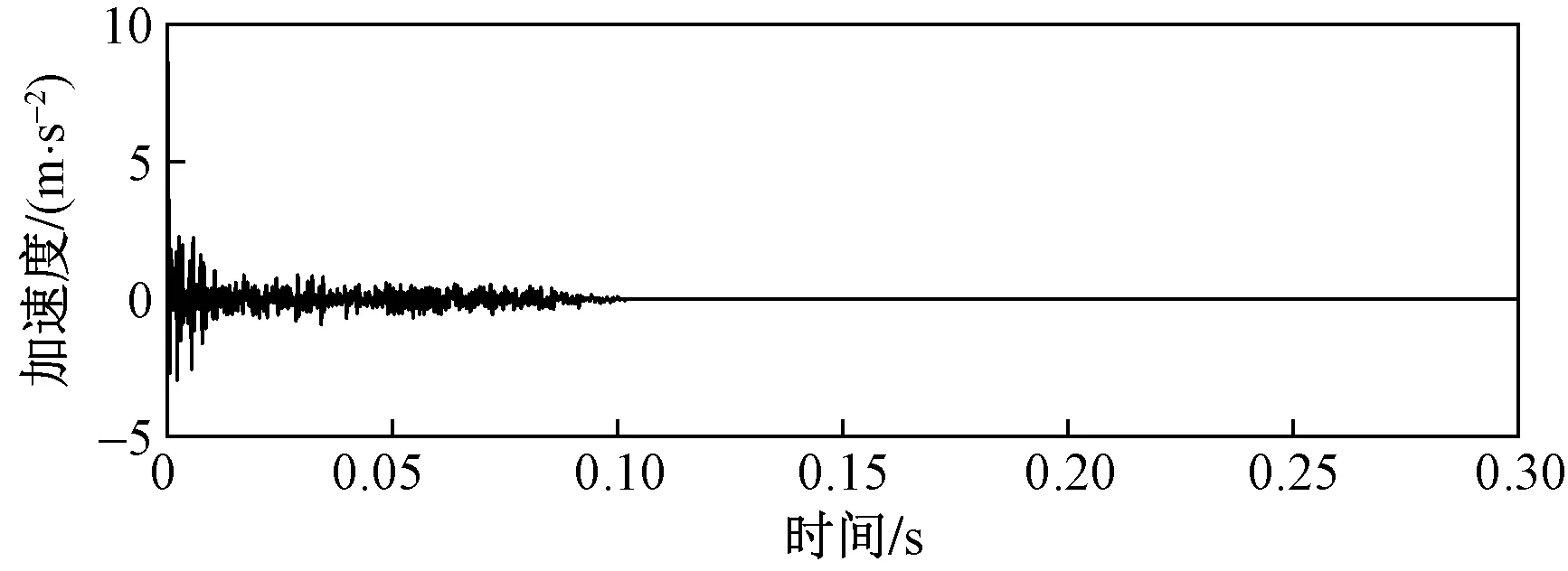
图4 螺栓紧固时1测点自相关预处理后时域信号

再依据中心频率原则确定分解模态数K值，进行VMD分解，具体步骤如下。

步骤1将进行过自相关降噪处理后的信号作为初始信号，初始模态参数设置为K=2，惩罚因子α=2 500，带宽设置为默认值0。

步骤2利用PC端信号分析软件运行VMD分解程序。

步骤3观察信号分解的中心频率，当第n层的中心频率小于第n-1层的中心频率或者中心频率相接近时，则确定模态数K=K-1。如果不满足上述情况，则K=K+1，继续进行步骤2的操作。

为验证自相关-VMD分解降噪法对输电铁塔塔材振动信号降噪的有效性。依照自相关-VMD分解降噪法流程，对进行过自相关预处理的1测点振动数据(图4)进行VMD分解，得到不同模态分量下对应的中心频率如表3所示。

由表3可以看出，当VMD分解层数K=7时，IMF4的中心频率ω4=1 243.92 Hz，而IMF5的中心频率为ω5=1 120.30 Hz第5分量中心频率相比第4分量中心频率较低，达到VMD分解结束的要求，因此选取K=6作为VMD分解层数。

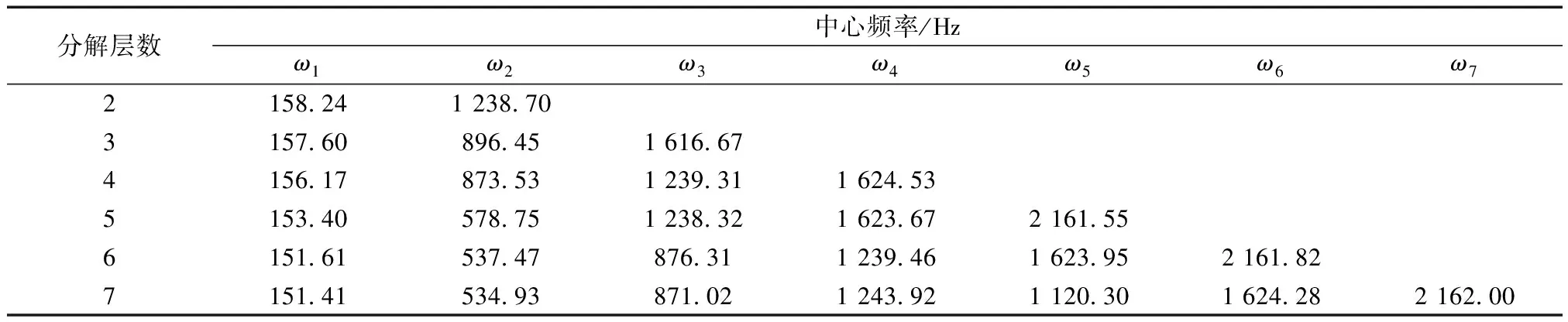
表3 螺栓紧固时1测点VMD分解中心频率

对信号进行VMD分解后，求解各IMF分量与经自相关预处理后的振动信号之间相关系数(表4),对相关系数大于0.2的模态分量进行重构。最后分别对重构信号和原信号进行FFT变换，对比两信号的频谱图(图5)，验证降噪方法的可行性。

表4 螺栓紧固时1测点各IMF分量与经自相关预处理后的振动信号之间的相关系数

如图5所示，将原信号(图5中黑线)与降噪之后信号(图5中蓝线)在频域上进行对比。可以发现，降噪之后的信号将初始信号的低频部分剔除，共振频率对应的峰值得到很好的保留，非共振的噪声引起的杂波信号得到抑制。因此自相关-VMD降噪在保留原始信号的同时，能够有效地将信号中的噪声成分剔除，可以更好地找出螺栓完全松动前后振动信号的特征频率，得出螺栓是否完全松动。

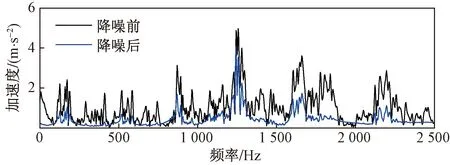
图5 螺栓紧固时1测点降噪前后频谱对比

3.2 自相关-VMD降噪效果评价

对降噪处理方法的降噪效果进行评价，一般利用信噪比(signal noise ratio, SNR)和均方根误差(root mean square error, RMSE)进行衡量[13-14]，其中SNR越大而RMSE越小，表明降噪方法的处理效果越好。其中信噪比和均方根误差的计算公式为

(8)

(9)

为评价所用降噪方法的降噪效果，分别利用小波包软阈值降噪，EMD降噪，VMD降噪3种处理方法分别对螺栓紧固时1测点原始振动加速度信号进行处理。3种降噪处理方法的降噪指标如表5所示。

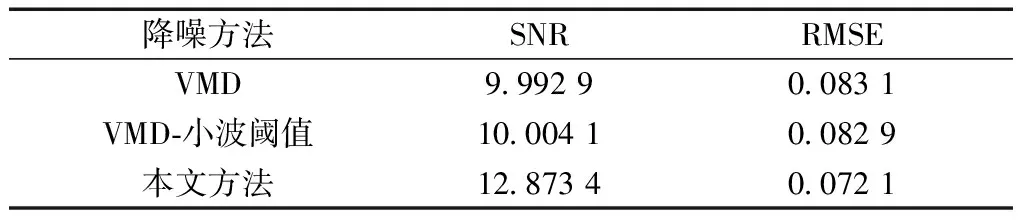
表5 降噪效果对比

对比3种降噪算法的降噪效果发现，本文方法优于VMD降噪和VMD-小波阈值两种处理方法，可以按照上述自相关-VMD降噪法对螺栓完全松动前后各测点的振动数据依次进行处理。

3.3 输电铁塔螺栓完全松动前后各测点振动频谱分析

按照上述自相关-VMD降噪法对螺栓完全松动前后各测点的振动数据依次进行处理，分别得到螺栓完全松动前后各测点降噪之后的频谱图，如图6～图9所示。

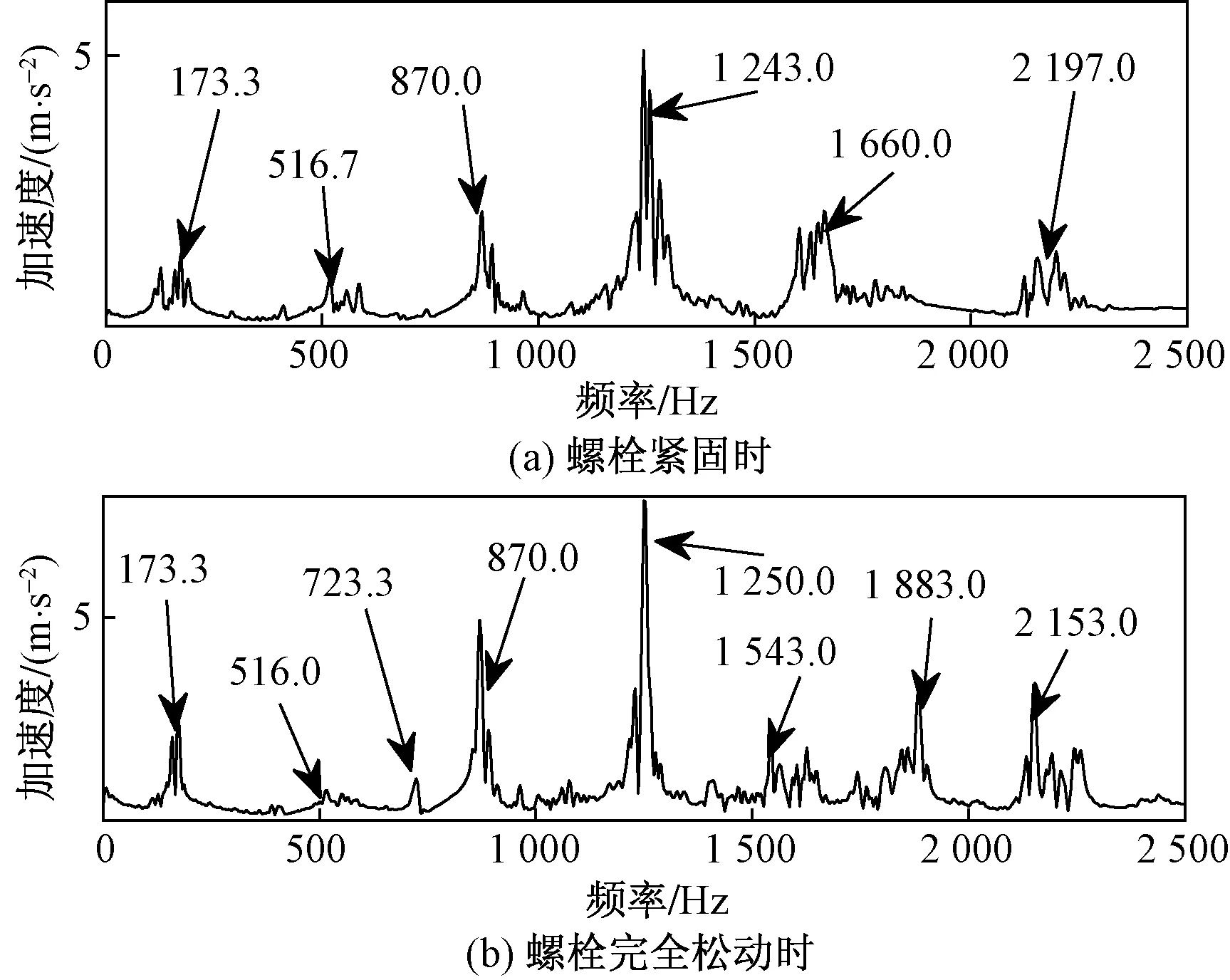
图6 螺栓紧固及完全松动时1号测点频谱

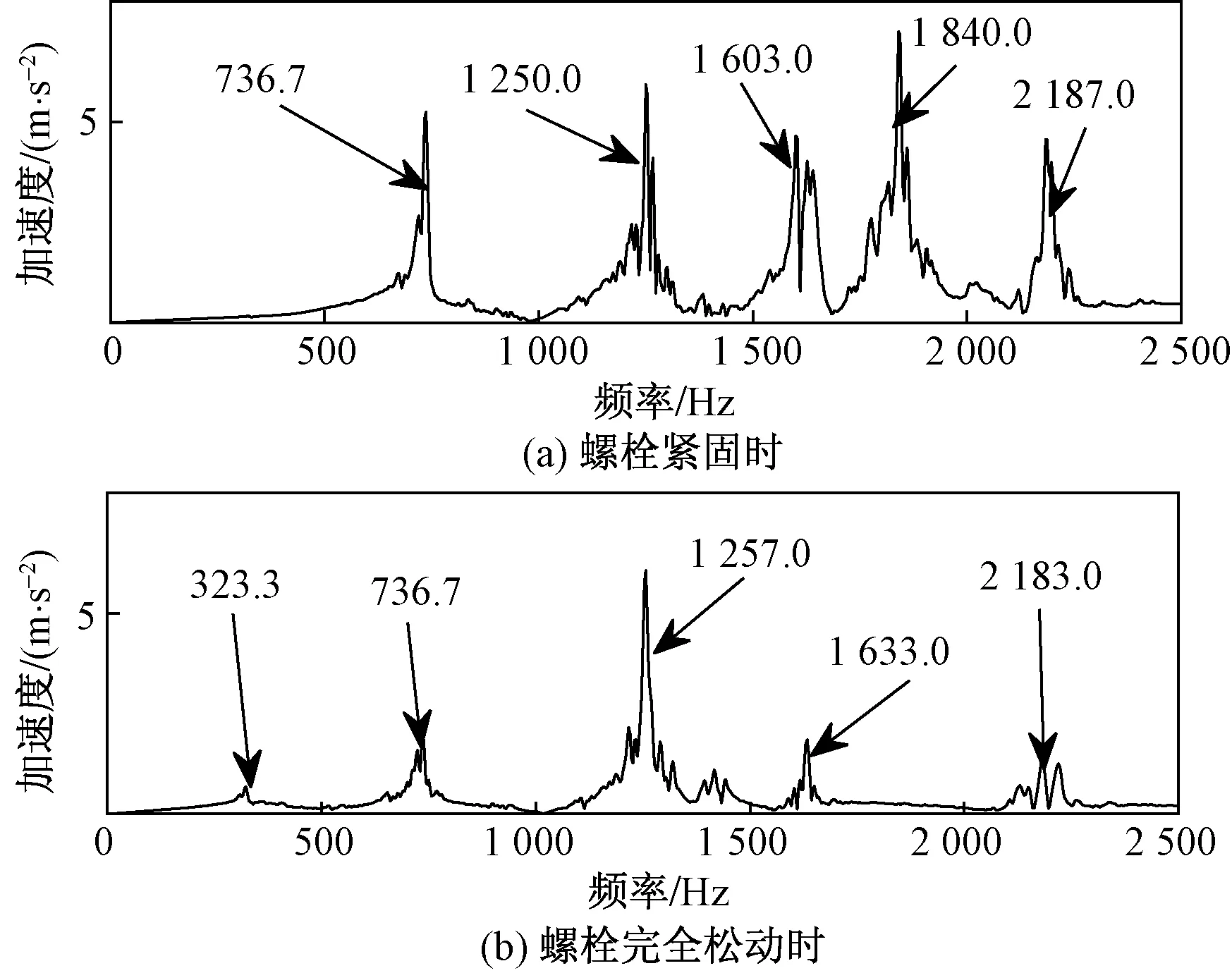
图7 螺栓紧固及完全松动时2号测点频谱

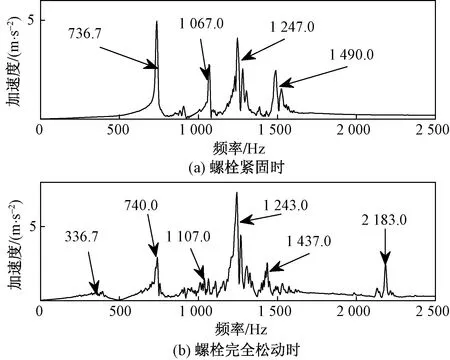
图8 螺栓紧固及完全松动时3号测点频谱

图9 螺栓紧固及完全松动时4测点频谱

如图6所示，螺栓发生完全松动前后，1测点振动频谱图主峰对应的频率值没有发生改变，但是在螺栓完全松动后，原处于1 660 Hz的峰值消失，而在723.3、1 543、1 883 Hz出现小的峰值。完全松动前后频谱图有微弱变化。

如图7所示，螺栓发生完全松动前后，2测点振动频谱图主峰对应的频率值由1 840 Hz变为1 257 Hz，而且在螺栓完全松动后，原处于1 840 Hz处峰值消失，并在323.3 Hz处出现小的峰值。完全松动前后频谱图变化较大。

如图8所示，螺栓发生完全松动前后，3号测点振动频谱图主峰对应的频率值由736.7 Hz变为1 243 Hz，而且在螺栓完全松动后，在336.7 Hz和2 183 Hz处出现小的峰值。完全松动前后频谱图变化较大。

如图9所示，螺栓发生完全松动前后，4号测点振动频谱图主峰对应的频率值由733.3 Hz变为1 243 Hz，而且在螺栓完全松动后，原处于1 760 Hz处的峰值消失，并在336.7、1 633、2 133 Hz处出现小的峰值。完全松动前后频谱图变化较大。

4 分析及讨论

综合以上频谱图的对比，各个测点在输电铁塔螺栓发生完全松动后，其频谱图都发生改变，因此各个测点振动频谱图的变化都可作为螺栓完全松动的判断依据。通过分析，发现以下问题并对其加以论述。

(1)由于1测点距离待测螺栓较远，所在的角钢质量较大，并且该角钢通过多处螺栓共同固定，当其中一个螺栓完全松动，对其刚度造成的影响较小，因此当待测螺栓发生完全松动后，1测点的振动频谱图变化较小，因此在之后的检测过程中，选取的振动测点尽量选取类如2号、3号、4号测点一样的测试位置。

在螺栓紧固时，对比1号、2号、3号、4号4个测点之间的频谱图峰值对应频率，发现其有较大的差异。因此可以判定在螺栓紧固时，螺栓连接的两个塔材相当于统一整体，因此各个测点在激振锤的作用下，各自发生自由振动，其振动频谱在各自的固有频率处出现峰值。

在螺栓发生完全松动后，互相对比1号、2号、3号、4号4个测点间的频谱图峰值对应频率，发现4个测点的主峰值都在1 250 Hz处[图6(b)中的1 250 Hz、图7(b)中的1 257 Hz、图8(b)中的1 243 Hz、图9(b)中的1 243 Hz]，而且峰值对应频率有相似之处。因此可以判定在螺栓发生完全松动后，由于激振点和1号、2号测点同在1塔材，其振动依然为自由振动，其振动频谱在各自的固有频率处出现峰值，因此由于刚度下降，其频谱峰值对应的频率呈现下降的趋势；而3号和4号测点所在2塔材不再和1塔材是统一整体，当用激振锤对塔材1施加脉冲冲击信号时，塔材1发生振动，碰撞塔材2，使得塔材2一起振动，因此现在塔材2发生的振动是由塔材1引起的受迫振动，因此3号和4号测点的主峰值和1号、2号测点一致，除此之外，发现螺栓完全松动后3号和4号测点仍保留松动前的振动成分，综上可以得出在螺栓完全松动后，2塔材的振动由受迫振动和自由振动共同影响。

综合1号、2号、3号、4号测点在待测螺栓完全松动前后振动信号的频谱特征，发现选取距待测螺栓最近的两测点(2号和3号)灵敏度最高。因此在实际工况对螺栓进行检测时应尽量保证传感器靠近待测螺栓。

(3)按照同样的方法，可检测其他位置连接螺栓的松动故障，为实际运行中输电铁塔螺栓松动检测提供借鉴。受实验条件所限，本实验采用压电加速度传感器测试塔材振动响应，实际运行的输电铁塔可采用激光测振仪进行非接触测试。

5 结论

利用激振锤人为激振输电铁塔，利用压电加速度振动传感器测量输电铁塔螺栓完全松动前后的振动信号，通过对比频谱图，得出了输电铁塔螺栓完全松动故障的判断依据。得出如下主要结论。

(1)通过对现场测得振动信号进行自相关-VMD分解降噪处理，验证该方法在对输电铁塔塔材振动信号降噪的有效性。

(2)在螺栓完全松动前后，对比分析了各个测点的振动频谱图，得出各测点振动频谱图的变化都可作为螺栓完全松动的判断依据，但相比而言，距离松动螺栓较近的测点的判别效果优于其他测点。

(3)在螺栓完全松动前后，互相对比分析了各测点的振动频谱图，得出在螺栓紧固时，螺栓连接的两个塔材相当于统一整体，两塔材在脉冲激振的作用下发生自由振动；在螺栓发生完全松动后，在脉冲激振的作用下，激振点所在塔材发生自由振动，螺栓相连的另一塔材发生受迫振动和自由振动。