中高密度城市居住区热岛强度计算模型研究

刘衍 李奇 杨柳 张腾跃 刘加平

西部绿色建筑国家重点实验室, 西安建筑科技大学建筑学院, 西安 710055; † 通信作者, E-mail: yangliu@xauat.edu.cn

在全球城市化进程加快的大背景下, 城市的发展改变了原有的下垫面, 进而改变了区域的能量平衡[1-2], 导致城市室外热湿环境与郊区有很大的差异。城市热岛效应对居民热舒适度[3]、建筑能耗[4]以及建筑热工设计[5]等都产生一定的负面影响。随着人类生活需求和建筑节能需求的日益增长, 建筑热工设计、暖通空调设计、建筑节能设计以及城乡规划设计等成为营造室内适宜热湿环境并实现城乡建设领域“碳达峰”和“碳中和”的重要手段。对建筑热工设计而言, 拥有合理、可靠的室内外计算参数是关键。然而, 我国目前使用的室外计算参数通常根据累年气象资料计算得到, 未考虑城市热岛效应对室外气候环境的影响。

龙瀛等[6]对 63个城市街区形态的研究结果表明, 我国城市中心城区的城市形态总体上以中层高密度建筑(建筑密度>25%, 建筑层数在 3~7 之间)为主, 很容易产生城市热岛效应[7]。城市中心城区也是居民人口较为集中的地段, 城市热岛效应的负面影响波及的人口相对更多, 因此迫切需要考虑城市热岛效应对建筑热工设计的负面影响。

使用城市热岛强度对室外建筑热工设计参数进行修正是行之有效的办法[5]。城市热岛强度可以根据气象观测数据计算得到, 但我国气象观测站目前依然匮乏, 故构建适用于全国范围的城市热岛强度计算模型十分重要, 这需要建立在对热岛成因深刻认识的基础上。

Howard[8]首次发现城市热岛效应时, 就已经猜想出几乎所有现在公认的热岛成因。19 世纪后半叶, 全球气象观测网络的迅速发展为气候分析和城市气候研究积累了大量基础数据。20 世纪 70年代后, 地理信息系统和遥感技术的发展为研究热岛成因提供了种类繁多、数量庞大的数据[9]。近几十年,研究者从降雨、城市储热和植被覆盖率等角度分析城市热岛的成因[10-11], 探讨城市热岛效应的影响因素[7], 进一步加深了对城市热岛效应的认识。在此基础上, 研究者采用多元回归分析等统计分析方法构建计算城市热岛强度的统计模型[12-13]。然而, 这类模型大多基于一个或几个城市的数据构建, 考虑到城市系统的复杂性, 统计模型在其他城市, 尤其是城市热岛效应研究较少的中小城市的适用性有待商榷。同时, 目前仅从定性的角度给出热岛成因[14], 城市热岛强度与城市形态、气候及人口等因素间的关系仍不清楚, 并且因一些隐藏的阈值而变得更加复杂[15]。因此, 基于城市热岛效应形成的物理过程, 建立适用于全国范围的城市热岛强度计算模型是急需解决的工程问题。

20 世纪 60年代末期, 物理气候学被引入城市热岛效应的研究中。20 世纪 80年代后, 随着城市气象观测技术的迅速发展, 研究者通过观测获取城市通量数据, 并与城市下垫面参数相联系, 建立稳健的参数化方案[16], 为建立更精细、更复杂的基于物理过程的能量平衡模型提供支撑, 也为从下垫面变迁导致原有能量平衡发生变化的角度构建城市热岛强度计算模型提供了思路和研究手段。

2010年后, 一些学者基于地表能量平衡方程和城市通量参数化方案, 构建地表热岛强度和热岛各影响因素的关系式, 研究地表热岛效应的成因。Zhao 等[17]通过研究北美 65个城市的地表热岛效应,认为空气动力学阻抗是地表热岛效应的主因。Li等[18]指出, Zhao 等[17]采用波文比计算潜热通量, 会导致空气动力学阻抗对地表热岛强度的贡献度被高估 10%~25%。Li 等[18]也构建了地表热岛强度与净辐射、空气动力学阻抗、地表蒸散阻抗和地表蓄热量的关系式, 对北美 60个城市的地表热岛效应进行归因分析, 结果表明地表蒸散阻抗是地表热岛效应的主因。这种归因分析的方法是将城市化视为对郊区基础状态的扰动, 通过解析法求解能量平衡方程,以便构建地表热岛强度与各影响因素的关系式。与传统的统计模型相比, 这种基于城市热岛效应形成的物理过程构建城市热岛强度计算模型的方法具有更高的适用性, 在北美[17-18]和全球[15]的应用结果也表明该方法可以在大范围使用。

本文针对建筑热工设计中室外计算参数, 考虑城市热岛强度修正问题, 借鉴上述地表热岛强度计算模型的构建思路, 建立适用于全国的, 拥有中高密度建筑城市的城市热岛强度计算模型(针对室外空气温度)。同时, 用 2013年全球城市热岛数据集[19]以及西安(中国)[20]、伯明翰(英国)[21]、麦迪逊(美国)[22]和巴塞尔(瑞士)[23]的观测数据对模型进行验证。

1 城市热岛强度计算模型的构建

本研究采用的解析法为泰勒展开法。对多元函数f(x1,x2, …,xn)在点(xk1,xk2, …,xkn)处进行泰勒展开, 整理后得到下式:

将多元函数f(x1,x2, …,xn)作为计算气温的能量平衡方程, 分别用f(x1,x2, …,xn)和f(xk1,xk2, …,xkn)计算城市气温和郊区气温, 其差值即为城市热岛强度。式(1)右侧(xi-xki)为能量平衡方程中城市与郊区变量(如下垫面反照率)的差异, 用来描述下垫面的变化对该地区原有能量平衡的影响。从式(1)看出, 城市热岛强度计算为各影响因素产生的气温变化之和, 即从能量平衡差异的角度来描述城市热岛效应的形成。

但是, 多元函数泰勒展开式的二阶及高阶项中出现多个变量相乘的情况, 使其由线性问题变为非线性问题, 各因素产生的影响往往咬合不清, 无法对城市热岛效应各影响因素的贡献进行归因分析。因此, 本研究对多元函数泰勒展开式仅保留一阶项(一阶泰勒级数展开, first-order Taylor series expansion):

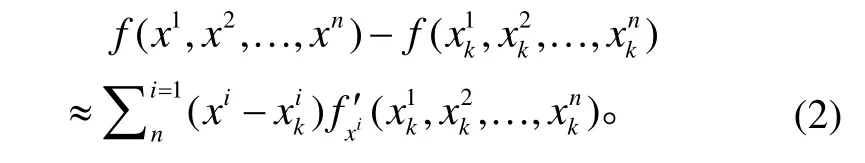
保证各变量的相互独立是使用一阶泰勒级数展开的前提。目前, 基于 Oke[24]提出的城市冠层概念,已开发出多种计算城市冠层气温的数值模型, 如麻省理工学院的 urban weather generator (UWG)[25]、亚利桑那州立大学的single-layer urban canopy model (ASLUM)[26]以及波士顿大学一种新的城市冠层模型(urban canopy model, UCM)[27]。这类模型考虑了城市下垫面与大气边界层间复杂的相互作用, 可以准确地模拟城市热环境。然而, 由于考虑了复杂和精细的物理过程, 此类模型中变量较多, 各变量间不能相互独立, 使用一阶泰勒级数展开构建的城市热岛强度计算模型会产生较大的误差。分别由耶鲁大学、波士顿大学和苏黎世联邦理工学院构建的数值模型 IBM (intrinsic biophysical mechanism)[17]、TRM (two-resistance mechanism)[18]以及 CGM (coarsegrained model)[15]具有较少的变量, 各变量间相互独立, 可用于构建城市热岛强度计算模型。但是, 这几种模型仅涉及地表温度。本研究将建立针对城市冠层气温的城市热岛强度计算模型, 变量尽可能少,且相互独立。

1.1 城市下垫面的简化

下垫面的性质对大气温度、湿度和风速等有很大的影响, 因此对城市下垫面的准确描述是建立模型的关键。早期, 使用平板(slab)模型对城市下垫面进行简化, 将整个城市简化为二维平面, 用空气动力学特性、辐射特性和热力学特性来描述城市建筑对地表能量平衡带来的影响, 适用于模拟空间尺度大的情况。20 世纪 90年代, 城市冠层的概念开始引入参数化方案中, 详细地描述城市冠层中的物理过程[28-29]。其中, Masson[29]建立的城市地表能量平衡模型(town energy balance model, TEB)最具代表性。该模型考虑了建筑高度、建筑密度以及街谷宽高比等城市下垫面参数对城市冠层中能量收支的影响, 并考虑自由大气与城市冠层之间以及城市冠层与下垫面之间的能量交换, 对城市冠层中的物理过程进行更详细的描述。

本文借鉴 TEB 模型对城市下垫面的简化方法(图1), 所提模型主要针对城市居住区, 故不考虑水体的影响。城市植被主要通过蒸腾作用和对辐射的阻隔来影响能量平衡, 降低环境温度[30]。由于本文模型针对城市冠层的平均气温, 不区分树冠层上方与下方的差异, 故仅考虑对城市冠层反照率的影响;对于植被的蒸腾作用, 用大叶模型(big-leaf model)计算植被的潜热通量。

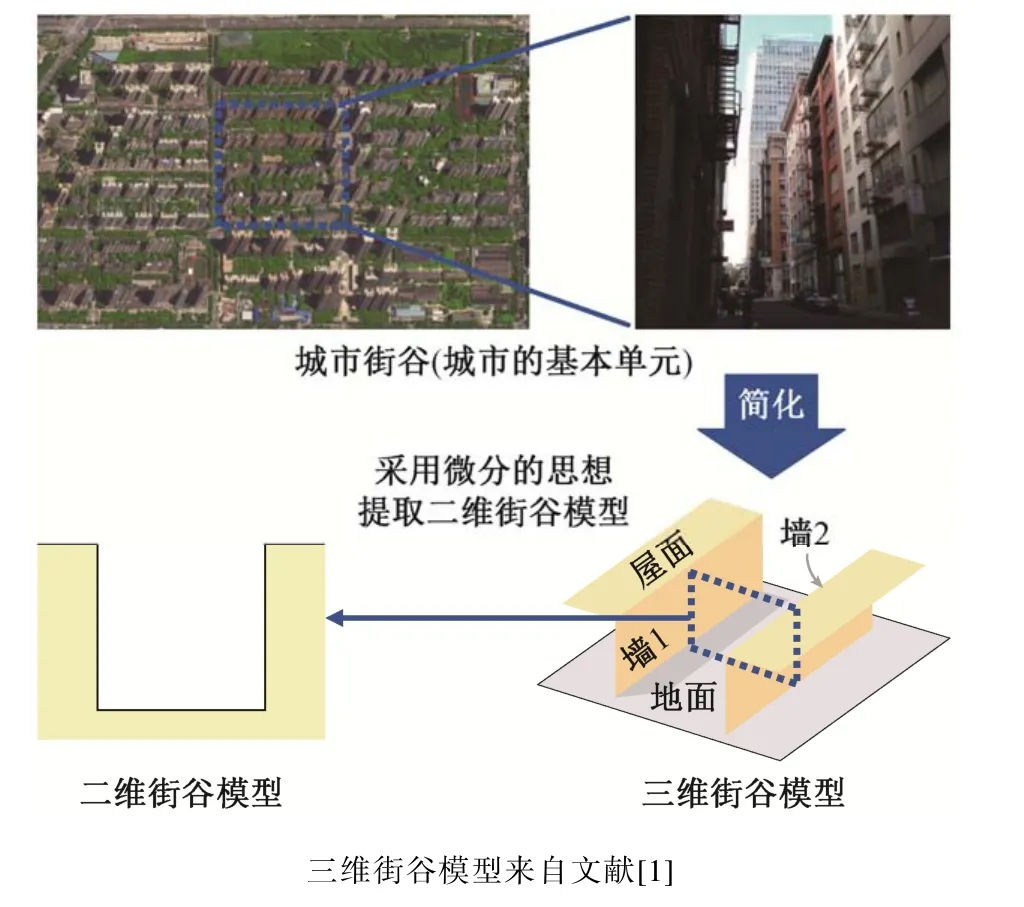
图1 城市下垫面的简化Fig.1 Simplification of urban underlying surface

1.2 城市下垫面能量平衡方程的构建

本文依据能量平衡原理, 建立下垫面能量平衡方程:

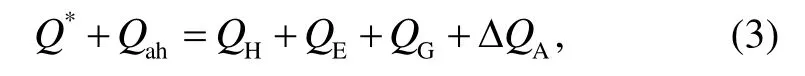
式中,Q*是地表接收的净辐射通量(W/m2);Qah是人为热通量(W/m2);QH是显热通量(W/m2);QE是潜热通量(W/m2);QG是下垫面蓄热量(W/m2); ΔQA是风对能量的输送量(W/m2), 在风场输送的作用下, 能量通过某一侧面而使城市冠层内能量增加或减少(ΔQA=Qin-Qout)。在实际数值模拟中, 都试图通过假设一个面积较大且相对均匀的城市下垫面作为研究对象, 这样就可以忽略能量输送的水平差异,ΔQA为零。同时, 考虑到Qah直接作用于城市冠层而不是下垫面, 故在城市冠层能量平衡计算模块中进行计算。因此, 本文将城市下垫面能量平衡方程简化为

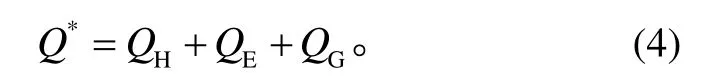
下垫面的辐射平衡可用下式表示:

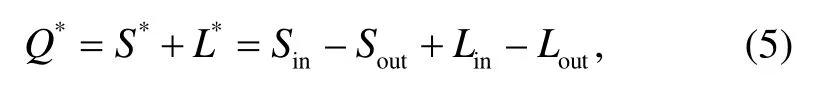
式中,S*和L*分别表示净短波和净长波辐射通量(W/m2); 下角标 in 和 out 分别代表入射和向上辐射;向上短波辐射通量Sout(W/m2)主要取决于下垫面反照率α:Sout=Sinα。Sin是入射短波辐射通量(W/m2),本文不考虑城市大气污染产生的影响, 故城市和郊区Sin都使用郊区气象站测得的数据。

Lin是入射长波辐射通量(W/m2), 当缺少该数据时, 可基于斯蒂芬-玻尔兹曼定律(Stefan-Boltzmann law)来计算:

式中,εa表示空气发射率;σ= 5.67×10-8W/( m2·K4),表示 Stephan-Boltzmann 常数;Ta表示大气边界层的平均气温, 使用郊区气象站测得的气温(K)作为输入数据。

Lout是向上长波辐射通量(W/m2), 分为从下垫面向大气发射的长波辐射通量和从下垫面反射的长波辐射通量, 计算公式为

式中,εs是下垫面的平均比辐射率,Ts是下垫面的平均表面温度(K)。

按照空气动力学阻抗(ra)的概念进行参数化,建立QH与Ts的关系式:

式中,ρ是空气密度(kg/m3),cp是干空气的恒压比热容(J/(kg·K)),ra是空气动力学阻抗(s/m)。

为了保证显热通量与潜热通量之间相互独立,采用大叶模型计算QE:

式中,Lv是汽化潜热(J/kg),qsat(Ts)是处于饱和状态时的比湿(kg/kg),qa是空气的比湿(kg/kg),rs是地表蒸散阻抗(s/m)。

将式(5)~(9)代入式(4), 可以得到下垫面能量平衡方程:

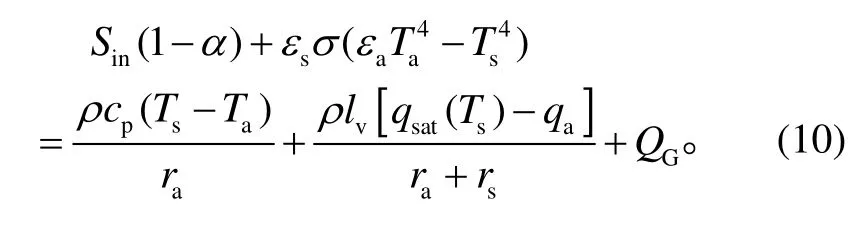
通过一阶泰勒级数展开, 对式(10)中的非线性项εsσTs4和qsat(Ts)进行线性化处理:

式中,qsat(Ta)是饱和状态下的比湿(kg/kg);q′sat,s(Ta)是相对于Ta的导数。本文中QG使用 OHM (objective hysteresis model)模型[31]进行计算。OHM 模型中Q*与QG之间存在相位差, 表达式为

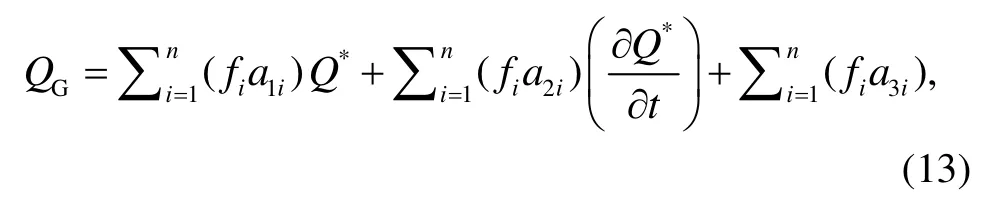
式中,i是不同的表面类型,fi是它们的权重, 表示类型i占据的表面参数;a1i反映QG对Q*的依赖程度,a2i反映Q*相对于QG的滞后时间(h),a3i反映QG与其他量之间的关系(W/m2)。

将城市化视为在郊区基础状态上的扰动, 用 Δ表示下垫面变迁导致城市与郊区α,εs,ra,rs和QG的差异(例如 Δα=αu–αr, 其中αu和αr分别是城市和郊区下垫面的反照率), 通过数学解析, 建立地表热岛强度(ΔTs)与能量平衡方程中各变量差异(Δα, Δεs,Δra, Δrs和 ΔQG)的关系式, 定量地研究下垫面变迁造成的能量平衡变化对 ΔTs的影响。对式(14)进行一阶泰勒级数展开, 可以得到城市地表热岛强度计算模型:

1.3 城市冠层能量平衡方程的构建

本文模型以城市冠层空气为对象, 并且不考虑空气体蓄存热量的影响, 依据能量守恒原理建立能量平衡方程, 将城市下垫面能量平衡计算模块获得的下垫面平均表面温度(Ts)作为边界条件。城市冠层能量平衡方程如下:

式中,Qc表示城市冠层与其上方大气之间的热通量(W/m2),Qs表示城市冠层与下垫面之间的热通量(W/m2),Qah表示人为热通量(W/m2)。

考虑城市冠层与冠层顶部大气的显热通量传递阻力,Qc值的计算采用基于莫宁-奥布霍夫(Monin-Obukhov)相似理论计算得到的空气动力学阻抗(ra):

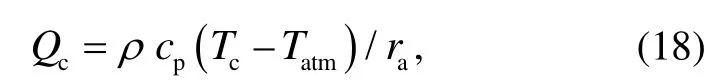
式中,Tatm是城市冠层上方大气的空气温度(K), 当缺少该数据时, 使用郊区气象站测得的气温值, 即Tatm=Ta;Tc是城市冠层的气温(K)。

将城市冠层与城市下垫面之间的热交换理解为城市下垫面通过湍流运动将热量传输到城市冠层空气中, 以城市下垫面能量平衡计算模块获得的Ts作为边界条件, 使用湍流扩散系数Ch(m/s)对Qs进行参数化处理:

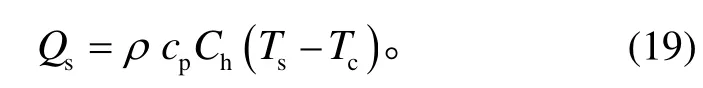
计算过程中的关键问题是Ch的确定, 以往的研究中常通过经验公式计算得到[29,32]。本文模型基于城市冠层内实际的气流特性计算Ch, 以便提高模型的精度。与城市冠层上方的风廓线近似对数分布不同,Macdonald[33]在风洞中的测量结果表明, 城市冠层中的风廓线更接近指数分布:u(z) =u(H) exp(-a(H-z) /H)。Coceal 等[34]基于 Macdonald[33]的研究成果,建立城市冠层湍流扩散率分布函数K(z):

式中,K(H) =kvu*(H-d), 是城市冠层顶部的湍流扩散率;H是平均建筑高度(m);z是垂直高度(0≤z≤H);kv是冯·卡门常数, 取 0.4;d是零平面位移高度(m);u*是摩擦速度(m/s);a是经验风速衰减系数。

体检工作均由工作经验丰富的相关人员统一完成,进行手肘正中位置进行静脉采血,以碘酒进行注射器、体检人员手肘消毒,所有人员均在同一环境、同一针头规格、同一操作方式下完成整个体检采血工作。

Li 等[27]基于湍流扩散率分布函数, 对z0h到z1=z0m+d高度的湍流扩散率进行积分, 并求倒数得到墙面和路面湍流扩散系数(C′h)的计算公式:

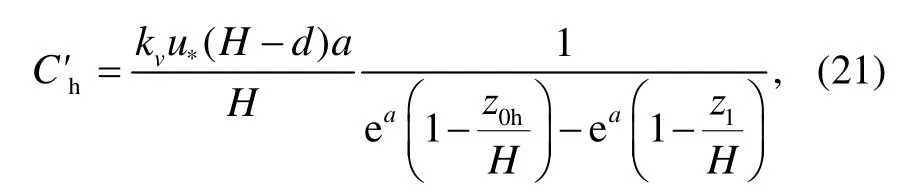
式中,z0m是动量空气动力学粗糙度长度(m),z0h是显热空气动力学粗糙度长度(m)。

在城市下垫面能量计算模块中, 计算得到城市下垫面的平均表面温度。因此, 采用一个整合的参数Ch计算城市下垫面与城市冠层空气之间的总热通量:

本文模型基于 Kikegawa 等[35]提出的建筑能量模型(building energy model, BEM)框架计算建筑物的人为热排放, 不考虑居住区内交通等热源产生的影响。由于城市下垫面能量平衡计算模块中没有对城市冠层的各部分(墙面、路面和屋面)的辐射收支单独进行计算, 并考虑到城市居住区建筑中室内人体代谢和设备散热产生的热负荷在整个人为热中占比较少[36], 本文模型只考虑通过围护结构的传热以及通风对室内产生的热负荷, 包括显热负荷和潜热负荷两部分。

h是围护结构的传热系数(W/(m2·K)),Tin是室内目标温度(K),βin是室内热交换效率,va是通风速率(m3/h),qa和qin分别是室内外空气的比湿(kg/kg)。

人为热通量由建筑能源系统的能耗(Ec)和由建筑能源系统搬运到室外的室内热量组成:

式中,Hout=φpHin, 是从室内排向室外的显热通量(W/m2);Eout=φpEin, 是从室内排向室外的潜热通量(W/m2);φp是在室人数与最大在室人数之比; COP代表建筑能源系统的性能。

将式(18)、(19)和(25)代入式(17), 建立城市冠层能量平衡方程, 经整理后得到城市冠层气温计算模型:

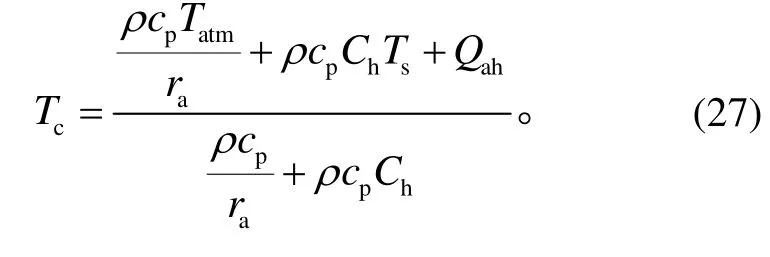
通过多元函数一阶泰勒级数展开, 建立城市热岛强度计算模型:

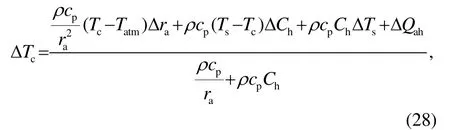
式中, Δra, ΔCh, ΔTs和 ΔQah与式(15)中类似, 分别为下垫面变迁导致的能量平衡方程中各变量的差异。

1.4 城市热岛强度计算模型框架和步骤

如图2 所示, 城市热岛强度计算模型的输入主要分为两类: 1)下垫面的参数信息, 包括建筑高度、建筑密度、垂直面积比(建筑垂直表面的面积与水平总面积之比)、高宽比以及植被覆盖率; 2)气象数据, 包括太阳辐射、气温、气压、相对湿度和风速。基于这两类基础参数计算反照率、发射率和空气动力学阻抗等变量, 以便得到辐射热通量、显热通量和潜热通量等。上述这些通量信息共同构成城市下垫面能量平衡计算和城市冠层能量平衡计算两个模块, 这两个模块共同构成最终的城市热岛强度计算模型。同时, 由城市下垫面能量平衡计算模块得出的下垫面平均表面温度(Ts)也作为城市冠层能量平衡计算模块的边界条件。

图2 城市热岛强度计算模型的输入输出Fig.2 Input and output of the urban heat island intensity model

本文模型的计算框架如图3 所示, 模型主要由城市下垫面能量平衡计算模块和城市冠层能量平衡计算模块组成.每个模块由太阳辐射、长波辐射、显热通量等数个子模块组成, 最后通过解析法构建城市热岛强度计算模型。

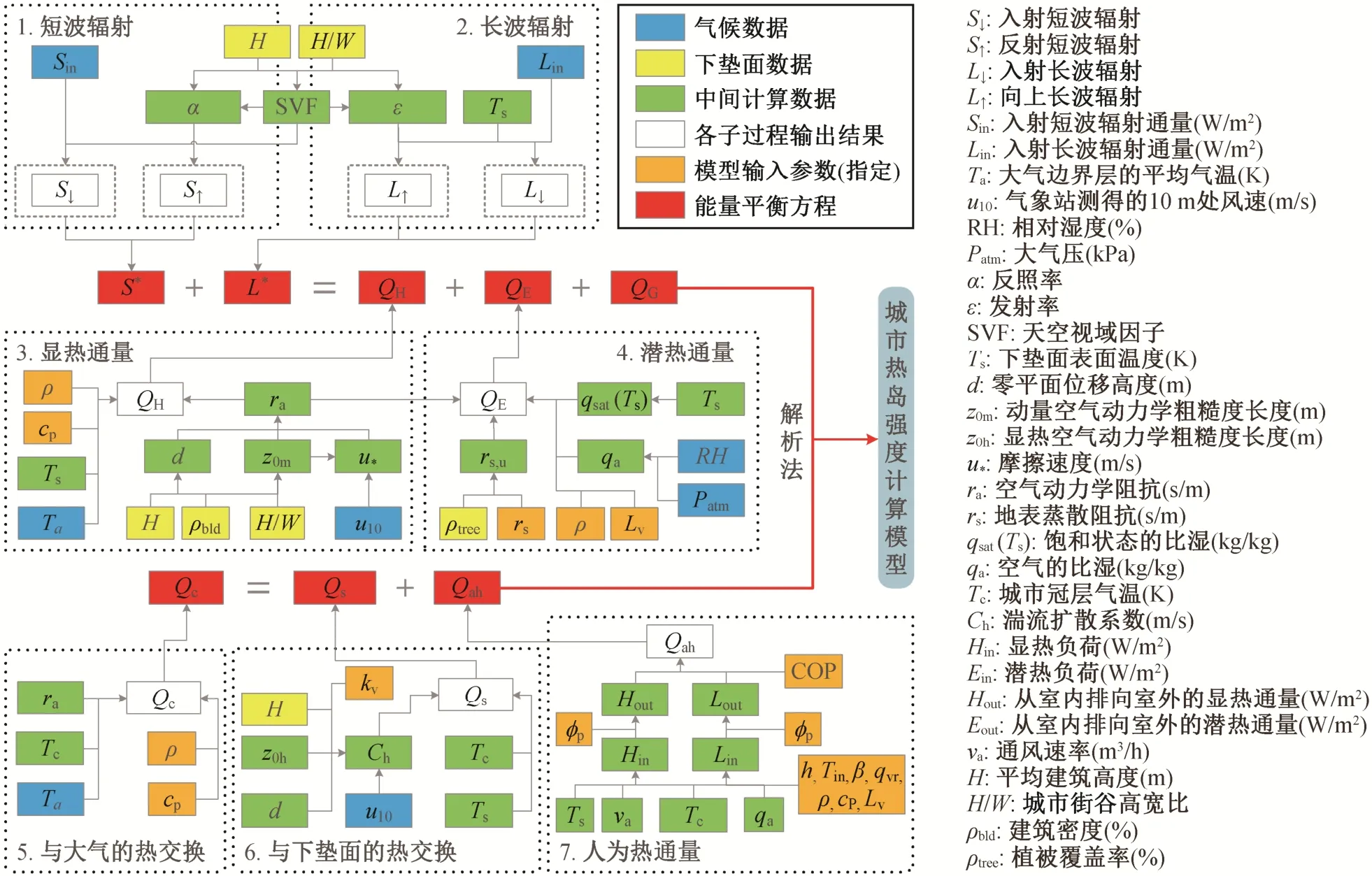
图3 城市热岛强度计算模型的计算框架Fig.3 Calculation framework of the urban heat island intensity model

2 模型验证

选用均方根误差(RMSE)、归一化平均绝对误差(NMAE)、平均偏差(MBE)、决定系数(R2)、纳什效率系数(NSE)和一致性指数(IA)作为模型性能评价指标。RMSE 和 NMAE 均用来衡量模型计算值与观测值之间的偏差, MBE 用来判断模型是否存在系统性偏差以及偏差的绝对幅度,R2反映模型的回归效果, NSE 描述模型计算值与观测值的一致性程度,IA 用来辅助评价模型性能, 克服 NSE 对较小数值不敏感的问题。

2.1 城市下垫面能量平衡计算模块的验证

对于式(10), 本研究采用泰勒展开方法, 将原本含有非线性项的一元四次方程转化为简单的一元一次方程(式(11)和(12))。在进行泰勒展开时, 省略其二阶及高阶项, 仅保留一次项。我们采用以下数据集来验证这种做法的合理性: 本文模型的验证数据来自美国国家航天局(NASA)提供的 2013年全球城市热岛数据集[19]; 2013年的城市背景气候条件来自Modern Era Retrospective-Analysis for Research and Applications (MERRA)[37], 包括 2 m 高度处空气温度(Ta)、地表温度(Ts)、入射短波辐射(Sin)、风速(Ws)、空气比湿(qa)和大气压(patm)。

全球 3 万多个城镇数据的验证结果如图4(a)所示, 可见一阶泰勒级数展开后的精度非常高(RMSE= 0.05 W/m2,R2>0.99), 完全满足计算要求。从式(11)和(12)的函数结构可以看出, 影响结果准确性的关键是Ts与Ta的差异, 故本研究通过人为放大Ts与Ta的差异来分析其对误差的影响。从图4(b)可以看出, 当二者差异在 20℃左右时, 误差开始快速增加; 然而, 即使在极端情况(Ts与Ta的差异约为45℃, 现实情况下几乎不可能出现, 数据集中Ts与Ta的差异基本上在 5℃以内)下, 仅保留一阶项的计算精度仍然较高(RMSE接近 80 W/m2, NSE 约为0.6, 但 IA 超过 0.85,R2也在 0.99 以上)。

图4 一阶泰勒级数展开式的合理性验证Fig.4 Validation of the first-order Taylor series expansion

Manoli 等[15]构建了一个包含 3 万多个地区下垫面地表温度与空气温度之间关系的统计模型, 本文将城市下垫面能量平衡计算模块的计算结果与之进行对比验证, 城市植被覆盖率分别按固定值(ρtree=0.15)和变化值(ρtree= 0.53/(1 + exp[-0.0028(P- 1309)]))计算[15]。

郊区和城市下垫面表面温度的验证结果分别如图5(a)和(b)所示, 计算值与观测值均吻合良好。从表1 可知, 郊区下垫面表面温度验证结果的 RMSE= 0.98℃,R2= 0.96, NSE 和 IA 都超过 0.95, 模型的精度良好; 城市植被覆盖率按固定值和变化值计算的验证结果差距不大,R2都在 0.75 左右, IA 都超过0.85, 模型的精度较好, 但比郊区下垫面表面温度的验证结果稍差。原因在于城市下垫面的表征比郊区下垫面复杂, 模型中各变量的计算结果更容易出现误差。

表1 下垫面地表温度验证结果Table 1 Validation results of the surface temperature in the underlying surface

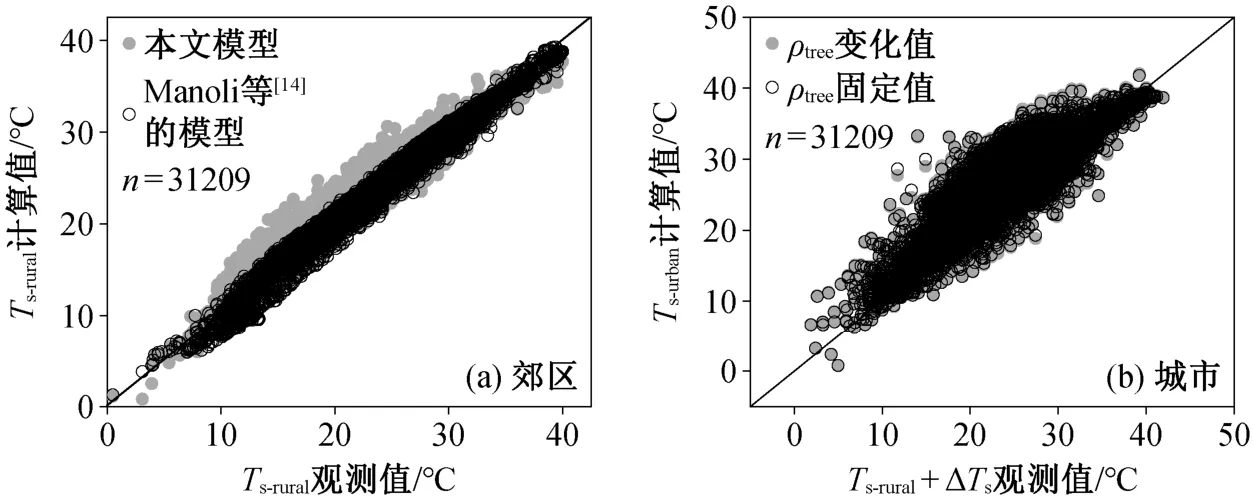
图5 使用全球城市热岛数据集对郊区(Ts-rural)和城市(Ts-urban)下垫面地表温度的验证结果Fig.5 Validation results of the surface temperature in rural (Ts-rural) and urban (Ts-urban) by the global urban heat island dataset

2.2 城市冠层能量平衡计算模块的验证

城市冠层能量平衡计算模块分别使用西安、伯明翰、麦迪逊和巴塞尔的气温观测数据进行验证。西安的数据为西安中心城区气象站和泾河气象站2016年的观测数据[20], 太阳辐射数据使用 Solcast 数据集[38]中的数据。伯明翰的数据来自伯明翰大学城市气候实验室建立的高密度气象观测网络[21], 本研究使用该网络中 5个台站(W006, W007, W009, W013和 W016)的数据。麦迪逊的数据来自威斯康星大学麦迪逊分校建立的由 150个气象台站组成的观测网络[22], 本研究使用麦迪逊中心城区一个半径为 500m 的区域内 6个台站(S.050.U, S.095.U, S.096.U,S.097.U, S.099.U 和 S.100.U)数据的均值。巴塞尔的数据为 2002年在瑞士巴塞尔进行的城市边界层实验[23]中 2002年6月10日至2002年7月10日的观测数据。

表2 汇总本文模型使用的城市下垫面参数信息。西安的城市下垫面参数信息来自刘衍等[39]的西安局地气候分类数据, 麦迪逊和伯明翰的信息分别来自 World Urban Database and Access Portal Tools (WUDAPT)的欧洲和北美洲局地气候分类数据[40-41], 按观测台站附近半径为 500 m 的区域选取城市下垫面参数, 巴塞尔的城市下垫面参数使用其数据集自带的数据[42]。

表2 城市下垫面参数信息Table 2 Parameter information of the urban underlying surface

图6 展示城市冠层能量平衡计算模块在西安的验证结果, 计算值与观测值均吻合良好。从表3 可知, RMSE 和 NMAE 分别为 0.94℃和 0.75℃, 模型的精度较高; MBE 为 0.32℃, 模型的计算结果高估了城市冠层的气温;R2, NSE 和 IA 都在 0.98 之上, 模型的计算结果与实测结果具有较好的一致性。图6(b)中, 5—7月的 RMSE 在 0.79~0.89℃之间, 11—1月在 0.79~0.98℃之间, 5—7月的计算精度稍高。Bueno 等[25]使用图卢兹的观测数据, 对他们开发的模型进行验证时也得到类似的结果(夏天 RMSE =0.7℃, 秋天 RMSE = 0.8℃, 冬天 RMSE = 1.1℃)。

图6 使用西安中心城区气象站气温数据(Ta-urban)的验证结果Fig.6 Validation results with the air temperature data (Ta-urban) from the Xi’an Central City Weather Station

从表3 和图7 可知, 城市冠层计算模块对温带海洋性气候(伯明翰)、温带大陆性湿润气候(麦迪逊)、亚热带海洋性气候(巴塞尔)这 3种类型的计算结果与实测数据均符合良好(RMSE = 0.61~1.45℃,R2> 0.95, NSE 和 IA > 0.9), 说明本文模型的城市冠层计算模块具有一定的适用性。

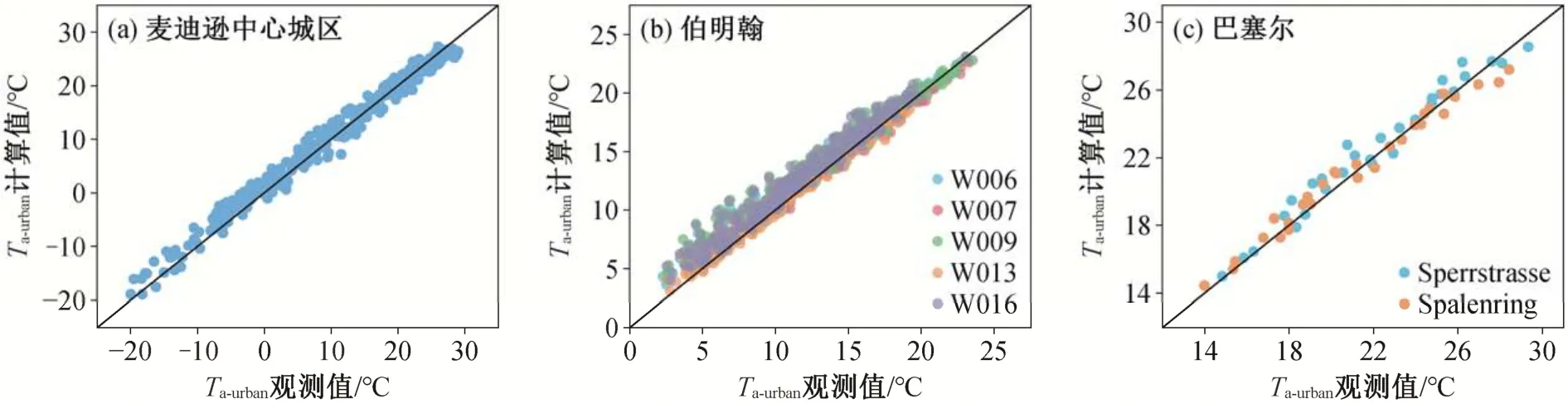
图7 对麦迪逊、伯明翰和巴塞尔城市冠层气温的验证结果Fig.7 Validation results of air temperature in the urban canopy in Madison, Birmingham and Basel

从表3 可知, 巴塞尔的 RMSE 为 0.63~0.80℃,其他城市的 RMSE 为 0.61~1.45℃, 模型对巴塞尔的计算结果与实测数据符合得更好, 这与巴塞尔数据中包含更精确的城市下垫面参数信息有关(其他几个城市的下垫面参数根据城市下垫面的分类数据估算得出); 在麦迪逊选择的观测台站位于 Mendota湖与 Monona 湖之间[22], 然而本文模型在构建过程中未考虑风速对能量输送的影响, 因此忽略了这两片湖泊对城市冠层气温的影响, 导致模型的计算结果出现系统性偏大的情况(MBE = 0.79℃), 验证结果相对较差(RMSE = 1.45℃)。

表3 城市冠层空气温度的验证结果Table 3 Validation results of air temperature in the urban canopy

将城市冠层计算模块与其他同类型计算模型的验证结果进行对比, 结果如表4 所示。本文模型在4个城市验证结果的 RMSE = 0.61~1.45℃, 与其他模型的精度相近, 表明本文模型的计算精度满足应用要求。

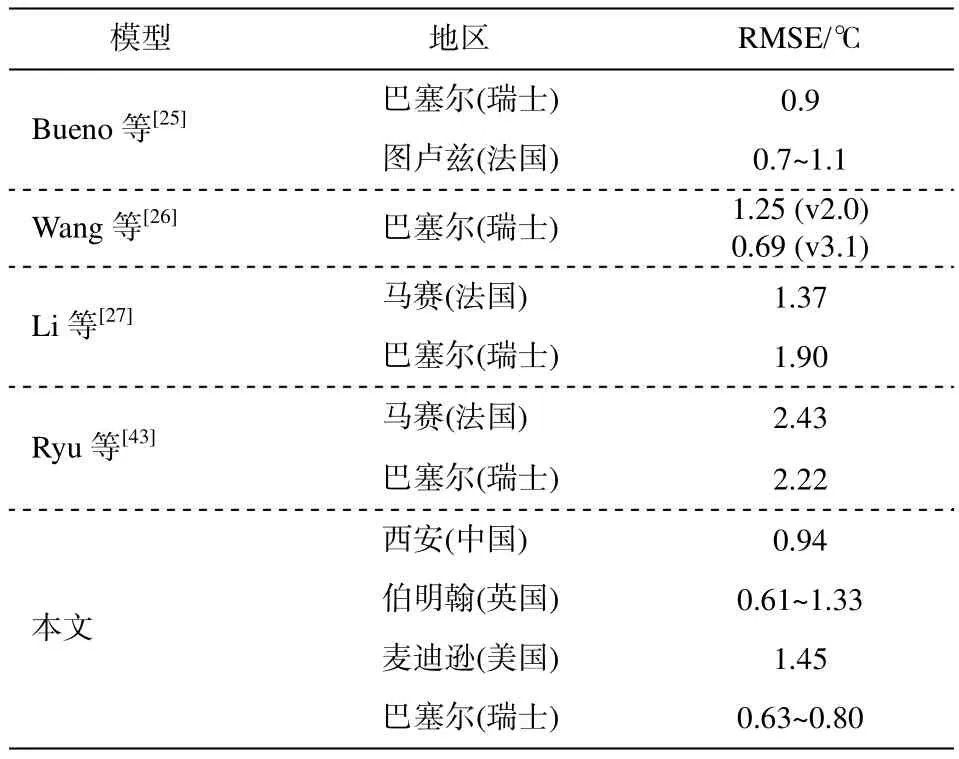
表4 不同模型的验证结果Table 4 Validation results of the different models

2.3 城市热岛强度计算模型的验证

使用上述 4个地区的观测数据, 对本文构建的城市热岛强度计算模型的计算误差进行分析验证,结果如图8 和表5 所示。虽然模型构建过程中采用的解析法为多元函数一阶泰勒级数展开, 忽略了二阶及高阶项, 但是也具有较高的精度(RMSE = 0.24~0.68℃,R2> 0.8, IA > 0.75)。

表5 城市热岛强度计算模型的验证结果Table 5 Validation results of urban heat island intensity model

图8 使用一阶泰勒级数展开构建的城市热岛强度计算模型合理性验证结果Fig.8 Validation results of developing the urban heat island intensity model by the first-order Taylor series expansion

需要说明的是, 伯明翰数据的模型计算结果出现系统性偏大的情况, 与当地太阳辐射通量较低有关(日均值仅为 0.51~34.58 W/m2)。当使用 OHM 模型计算下垫面蓄热量时, 较低的太阳辐射通量可能会高估下垫面释放的蓄热量。

2.4 城市热岛强度计算模型的敏感性分析

使用西安的数据对城市热岛强度计算模型进行敏感性分析。考虑到模型的输入数据分为下垫面参数数据和气象台站观测数据, 将西安全年的观测数据分为春、夏、秋、冬四季进行分析。分别计算各个季节气象数据的平均值, 结果如表6 所示。

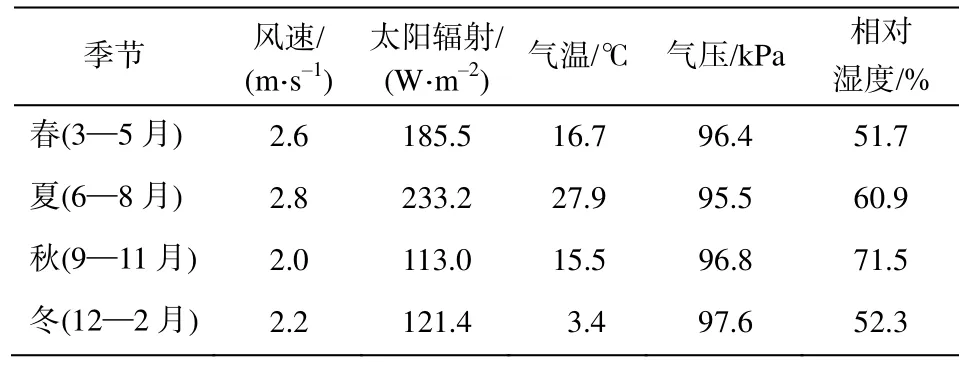
表6 不同季节气象数据的平均值Table 6 Average value of meteorological data in different seasons

本文模型中城市下垫面参数设置如下: 建筑高度为 9~21 m, 建筑密度为 25%~50%, 植被覆盖率为 5%~50%。同时, 设置基本案例如下: 建筑高度为 18 m, 建筑密度为 30%, 植被覆盖率为 15%, 高宽比和垂直面积比分别按建筑高度和建筑密度的数据计算得到。通过改变建筑高度等输入参数, 分析城市热岛强度计算模型的敏感性, 结果见图9。

图9(a)显示, 建筑高度较低时敏感性更强。较高的建筑会形成更多的阴影[44], 并且对大气的扰动更强, 具有较低的空气动力学阻抗[45], 有利于城市冠层空气与上层大气之间的热量传送, 从而形成较弱的热岛效应。

图9(b)显示, 建筑密度较大时敏感性更强。较大的建筑密度增加了建筑对天空的遮蔽度, 影响长波辐射散热。同时, 人为热排放也随着建筑密度的增加而增长, 导致城市冠层气温升高, 出现更明显的城市热岛效应, 这种现象在人为热排放较多的冬季更明显[46]。因此, 冬季城市热岛强度对建筑密度的敏感性更强, 在建筑密度较高时更明显。

图9(c)显示, 植被覆盖率较小时敏感性更强。城市不透水面积增加、潜热通量减少是城市热岛效应形成的重要原因, 植被覆盖率增加有利于提高潜热换热的相变吸热量, 对缓解城市热岛效应有利。同时, 植被蒸散发能力的季节性差异是城市热岛强度对植被覆盖率的敏感度存在季节性差异的重要原因。城市热岛强度对植被覆盖率的敏感程度夏季最强, 冬季最弱, 根据图9(c)中的拟合公式, 春季、夏季、秋季和冬季热岛强度的变化率分别为 0.08℃/10%, 0.12℃/10%, 0.06℃/10%和0.04℃/10%。

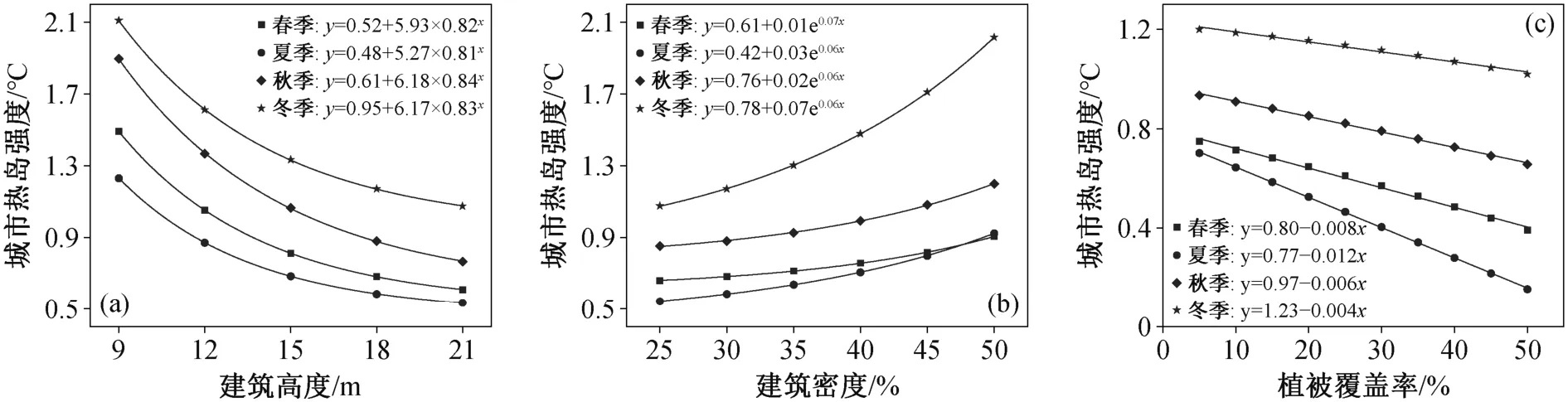
图9 城市下垫面参数敏感性分析Fig.9 Sensitivity analysis of parameters of urban underlying surface

选取各季节气象参数变化范围进行敏感性分析, 结果如图10 所示。城市热岛强度对气压的敏感度最低, 在四季气压变化范围内热岛强度最大变化仅为 0.003℃。城市热岛强度对风速的敏感度最大(尤其是风速较小时), 并在冬季对风速具有更强的敏感性, 原因是冬季人为热排放对热岛影响更显著[46], 而风是热量消散的重要驱动力。气温<17℃(>26℃)时, 与城市热岛强度负(正)相关, 这与采暖(降温)人为热排放的趋势一致。太阳辐射与城市热岛强度负相关, 这是因为与郊区相比, 城市下垫面蓄存热量的能力更强。当太阳辐射较低时(可能出现净辐射Q*为负的情况), 根据 OHM 模型, 城市下垫面可以释放更多储存的热量, 导致升温更明显;当太阳辐射较高时, 城市下垫面也可以储存更多的热量, 将限制城市升温。相对湿度也与城市热岛强度负相关, 较高的相对湿度意味着空气中可进一步容纳的水蒸气减少, 进而抑制植被向周围环境蒸散发水分的潜力, 此时城市与郊区植被覆盖率差异导致的蒸散量差异并不明显, 故城市热岛强度较低。

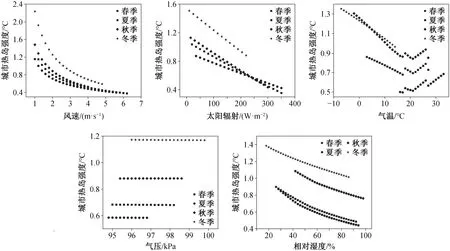
图10 气象数据敏感性分析Fig.10 Sensitivity analysis of meteorological data

3 结论

本研究基于城市热岛效应形成的物理过程, 通过解析法求解能量平衡方程, 建立城市热岛强度计算模型, 得到以下结论。

1) 在城市下垫面能量平衡计算模块中, 通过假设一个面积较大且相对均匀的城市下垫面来忽略风速对能量的输送量。考虑到人为热排放直接作用于城市冠层气温, 而不直接作用于下垫面, 因此在城市冠层能量平衡计算模块中加以考虑。采用大叶模型计算潜热通量, 保证显热通量与潜热通量之间相互独立。使用 2013年全球城市热岛数据集对该模块进行验证, 证明在自然下垫面和城市建成区下垫面都具有较高的计算精度(郊区 RMSE < 1℃, 城市RMSE < 3.2℃)。

2) 在城市下垫面能量平衡计算模块中, 基于城市冠层内的实际气流特性来计算湍流扩散系数, 以便考虑城市冠层与下垫面的热交换过程。同时, 以建筑能量模型为框架来计算人为热排放通量。使用西安、麦迪逊、伯明翰以及巴塞尔的观测数据进行验证, 结果表明本文模型的计算精度较高(RMSE <1.5℃), 与同类型模型相近, 并且模型计算结果与实测结果有很好的一致性(IA > 0.9)。

3) 使用中外多城市多源数据验证了城市热岛强度计算模型构建过程中仅保留一阶项的合理性,本文模型构建过程中仅保留一阶项取得较高的精度(RMSE < 0.7℃)。

4) 使用西安的数据对城市热岛强度计算模型进行敏感性分析, 结果表明城市下垫面参数的敏感性受到气候条件影响, 植被覆盖率的敏感性夏季最高, 冬季最低; 冬季建筑密度的敏感性显著高于其他季节, 并在建筑密度较高时更明显; 建筑高度的敏感性受气候条件的影响不大, 建筑高度较低时敏感性更显著。气象数据敏感性分析结果表明, 气压的敏感性最低(热岛强度仅变化 0.003℃), 风速的敏感性最高, 尤其是风速较低时。

本文研究结果可为解决受热岛影响的室外建筑热工设计参数修正问题提供支撑, 也可为从物理层面探讨下垫面变迁对室外空气温度的影响, 加强热岛成因的定量化研究提供基础模型。

致谢 雷丁大学罗志文教授、伯明翰大学城市气候实验室、北温带湖泊项目(North Temperate Lakes)团队和巴塞尔城市边界层实验项目(Basel Urban Boundary Layer Experiment, BUBBLE)团队在获取观测数据方面提供帮助, 谨致谢忱。