不同渗透率下风机惯量提升控制研究
刘泽宇,赵兴勇,唐震
(1.山西大学 电力与建筑学院,山西 太原 030000; 2.国网山西省电力公司 电力科学研究院,山西 太原 030001)
0 引 言
近年来,随着全球范围内化石燃料逐渐枯竭,风电光伏等新能源机组得到广泛应用[1]。因此,结合风电机组的运行特点和转动惯量的产生原理,发现风电机组转动惯量的主要影响因素,研究新能源机组转动惯量的测量技术,对于改善电网动态特性提供更多的参数支持,具有非常重要的实际意义。
风电的随机性大大提高了电网的不确定性。为了改善整个电网,文献[2]基于风机运行状况,在确定风-火机组参与调频参考值基础上,对风电机组调频功率进行动态分配。文献[3]提出了变参数控制策略,该策略能够根据系统频率变化实时修改参数,对系统提供动态有效储能。上述文献均基于系统风机占比不变情形下进行分析,并没有验证不同风机占比下调频方案可行性。本文在考虑不同风机渗透率以及风电机组运行工况与风机惯量控制耦合关系的前提下,提出风机自适应惯量控制。在Simulink中搭建双机系统检验该控制方法是否能有效补偿系统惯量。
1 风机转动惯量
系统在额定频率正常运行时,同步机转子以额定转速转动[4]的动能为:
(1)
式中:Ωn为同步机转子的额定机械角速度;J为转子转动惯量。同步机转子惯性时间常数HS指在转子上施加额定转矩Tm后,转子从静止状态(机械角速度为0)加速到额定运行状态(机械角速度为Ωn)所经过的时间,故有:
(2)
当同步机的极对数为1时,转子机械角速度Ωn与转子电角速度ω相等,故:
(3)
式中:Pn为同步机的额定功率;f0为系统的额定频率;f(t)为系统的瞬时频率。在t时刻内转子释放能量E(t)为:
E(t)=-1/2Jω(t)2
(4)
在t时间点输出的电磁功率Pe(t)即为该能量微分:
(5)
式(3)代入式(5)且一般f(t)≈f0,可表示为:
(6)
综上,风机接入电网惯量量测表达式为:
(7)
惯性时间常数量测表达式为:
(8)
由式(7)、式(8)可知,系统频率变化率相反数与同步发电机惯量支持的电磁功率成正比,因此虚拟惯量可以看作是系统频率的微分反馈控制。而实际中利用传感设备可测得系统某节点的频率,进而得到频率与时间的时域惯性,通过上式可得到转动惯量和惯性时间常数。
2 自适应惯量控制
根据风机[5]占比及机组运行工况,联合机组自身惯量特性和传统PID控制方法提出自适应惯量控制,此时风电机组调频功率给定为:
(9)
式中:KP、KD分别为惯性控制的比例、微分系数;Kw为不同渗透率风电场调频比例系数;ΔPw为附加有功功率设定值;Δf为系统频率偏差。
自适应惯量控制参数由式(10)动态给定:
(10)
图1为风机惯量控制图。控制算法的动态过程为:首先根据双机系统中风机占比确定风机调频比例系数Kw大小,使其满足:风机占比低,Kw取值尽可能小;风机占比高,Kw取值尽可能大。接着检测机组输出电磁功率Pe,转子转速ω,系统频率偏差Δf,判断频率偏差范围。若频率偏差小于死区,则不参与调频,参数控制函数值f(ωr,Pe) = 0,反之则参与调频;检测转子转速,若ωr<ωmin,则不参与调频,参数控制控制函数值f(ωr,Pe) = 0,若ωmin<ωr<ωmax,则参与调频。当系统参与调频时,根据文献[6]
中模糊逻辑规则表推理原则可知当频率偏差Δf较小时,则输出K2要尽可能小,K1绝对值尽可能大且为负值;当系统频率偏差Δf较大时,如果频率变化率为正,则输出参数要K2尽可能小,K1绝对值尽可能大且为负值;频率变化率为负时,则K2要尽可能大,K1尽可能大且为正值。进入下一周期,重复上述过程。控制过程如图1所示。
3 仿真验证
在Simulink下搭建双机系统仿真模型如图2所示。其中:G1为风电场,G2为额定容量200 MW的火电厂,并预备调频减载能力,设置风机风速为9 m/s,每台风机的额定容量为1.5 MW,各组风机数量分别为10台、20台和30台,调整火电厂出力保持系统总功率恒定为150 MW。对应的风电渗透率风别为10%、20%和30%。在20 s时负荷突增10 MW,观察系统频率以及风场有功波动情况,验证本文所提不同渗透率下风机惯量补偿策略可行性。

图2 仿真系统示意图
图3为发生负荷突增扰动频率/转速变化,可知当风机采取本文所提控制时能快速降低转子转速响应系统频率变化,相较于减载控制释放更多转子动能,为电网提供调频有功支撑,在结束调频后逐步提高转速,使其尽量相等于减载控制后转速水准,有效避免调频造成失速问题,保证机组运行稳定。

图3 负荷突增扰动下仿真结果
图4是发生负荷突增扰动下风机采取本文所提控制时控制器输出曲线。结合图3可知控制参数KP和KD在频率发生跌落时发生快速增加,使风机系统能在短时间内提供更多的控制输出有效加速系统频率恢复,进而减少系统频率的恶化。同时在调频结束之后,控制器不会出现超调现象,提高系统稳态恢复速度。
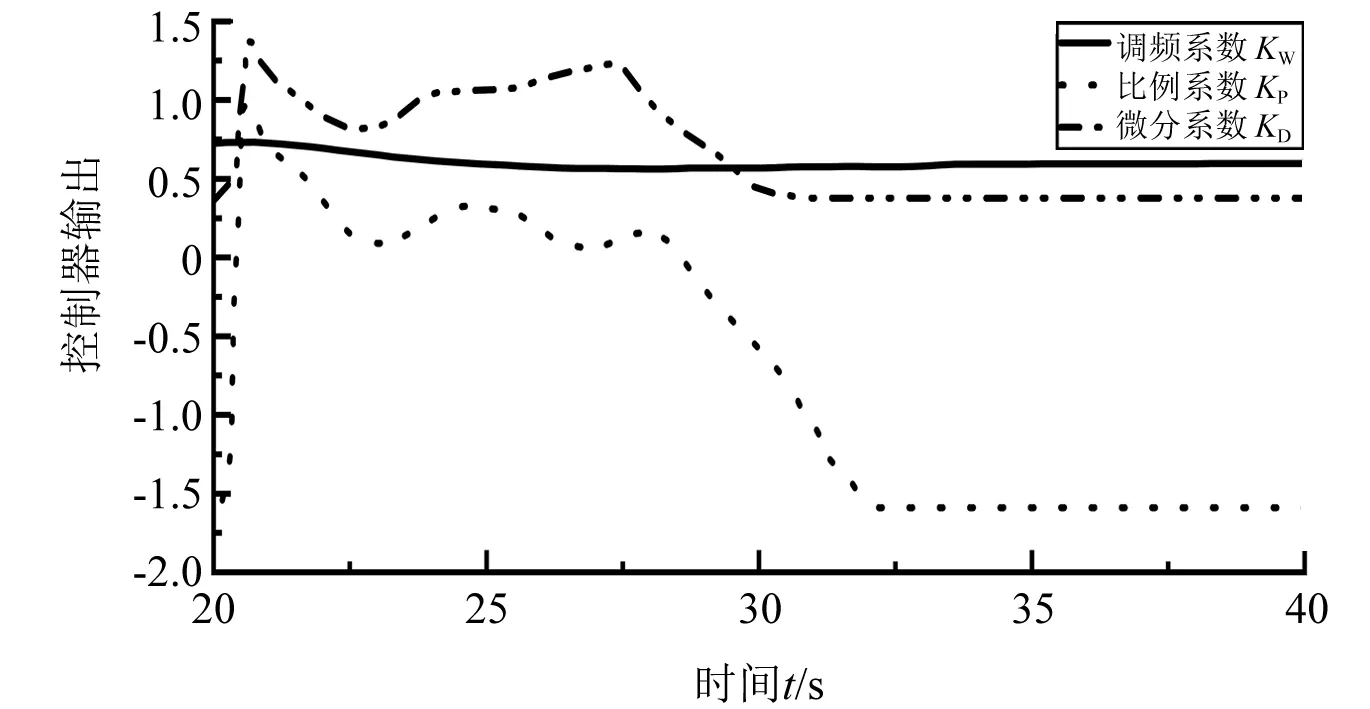
图4 控制器输出曲线
表1为有功负荷突增扰动、不同渗透率下风机最高有功出力。由表1可知,在相同的控制方式下,随着风机占比的提高,风电机组有功出力逐渐增加。风机在不同渗透率条件下均能够稳定、可靠地增发出力,为系统调频进行准备;风机采取传统转子减载控制时,通过降低转速释放转子中的动能,增加向电网输出有功为系统频率提供支撑;风机采取本文所提策略,通过识别系统频率变化来实时修改调节参数增加风机有功出力,使风机在不同运行条件下均能提供更加有效的惯量补偿。

表1 不同渗透率下风机最高出力
由以上分析可知,当系统总功率不变、风机渗透率逐渐增大时,将造成系统最大频率偏移逐渐增大,且均大于采取附加控制下的最大频率偏移量。采取本文所提控制策略的风机在系统发生频率跌落时能够更灵活有效地进行频率支撑。
4 结束语
本文针对不同渗透率下风-火系统对电网频率特性的影响,提出一种自适应惯量补偿策略,使风机能在频率发生扰动时维持频率稳定,得出如下结论。
(1) 通过分析风机转动惯量产生机理,得出风机惯量与系统频率变化率成反比,且风机能虚拟出远大于固有惯量的等效惯量。
(2) 研究不同风机渗透率下系统频率影响,得出随着风机占比提高,系统频率波动增大且风机调频出力逐渐提高,说明不同渗透率下风电场都可以采取辅助调频维持频率稳定。
(3) 分别在不同占比风机条件下进行负荷突增常见扰动仿真。结果表明,相较于传统的转子减载方法,该控制策略可以更好地提高系统频率响应特性,有效提高风电机组的运行稳定性。

