两道“新距离”问题引发的思考*

陈元中 (安徽省合肥市第一中学高三35班 230601)

指导教师 洪雨沛 (安徽省合肥市第一中学 230601)

1 对两道新定义类题目的思考

在高中数学中，新定义类题目因设问情境新颖，能够凸显学生的能力与素养，经常受到出题人的青睐．除了我们最熟悉的欧氏距离外，其他“新”的距离常被设置成具体情境考查学生．下面两道题目分别定义了两种全新的距离．

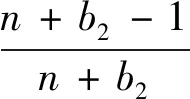
3 解题反思

4 解法溯源

4.1 等差模型

4.2 等比模型

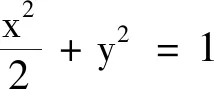
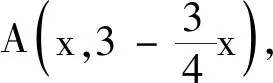
问题2在平面直角坐标系中，定义d(A,B)=max{|x1-x2|,|y1-y2|}为两点A(x1,y1),B(x2,y2)的“切比雪夫距离”．又设点P及l上任意一点Q，称d(P,Q)的最小值为点P到直线l的“切比雪夫距离”，记作d(P,l)．

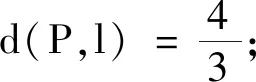
思路 其中①③的讨论见后文．

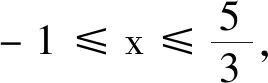
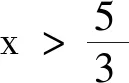
综上，①②③正确．

2 两种“新距离”

上述两个题目定义了两种不同的距离．经过查阅资料得知，我们最常使用的距离称为欧几里得距离，而问题1、问题2定义的这两种距离分别被称为曼哈顿距离和切比雪夫距离．距离究竟是怎样的数学概念，这三种距离有怎样的联系与区别，笔者在R2空间中对三种距离进行了深入的探讨．

2.1 距离的定义

我们所熟知的距离本质上是泛函分析中的一个基本概念．通过查询相关材料，我们能够得到距离的一般定义：

设X是任一非空集，对X中任意两点x,y，有唯一确定的实数d(x,y)与之对应且满足： ①非负性d(x,y)≥0，当且仅当x=y时d(x,y)=0；②对称性d(x,y)=d(y,x)；③三角不等式d(x,y)≤d(x,z)+d(z,y)．称d(x,y)为x,y之间的距离，(X,d)为度量空间．

我们不难发现欧氏距离显然满足上述定义．那么曼哈顿距离和切比雪夫距离是否满足距离的定义呢？

2.2 曼哈顿距离

在R2空间中，A(x1,y1),B(x2,y2)，则A,B两点的曼哈顿距离可表示为d(A,B)=|x1-x2|+|y1-y2|．

由曼哈顿距离的定义易证非负性与对称性，下面证明在曼哈顿距离下三角不等式是成立的：

设M(x3,y3)，则d(A,B)=|x1-x2|+ |y1-y2|，d(A,M)=|x1-x3|+|y1-y3|，d(M,B)=|x3-x2|+|y3-y2|，则d(A,M)+d(M,B)=|x1-x3|+|y1-y3|+|x3-x2|+

|y3-y2|≥|x1-x3+x3-x2|+|y1-y3+y3-y2|=|x1-x2|+|y1-y2|=d(A,B)．由此可知曼哈顿距离满足距离的定义．

曼哈顿距离在实际生活中的应用十分广泛．一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离可以用南北方向与东西方向的距离之和表示，而这种形式的距离也就是曼哈顿距离，因此曼哈顿距离又称为“出租车距离”(图1)．

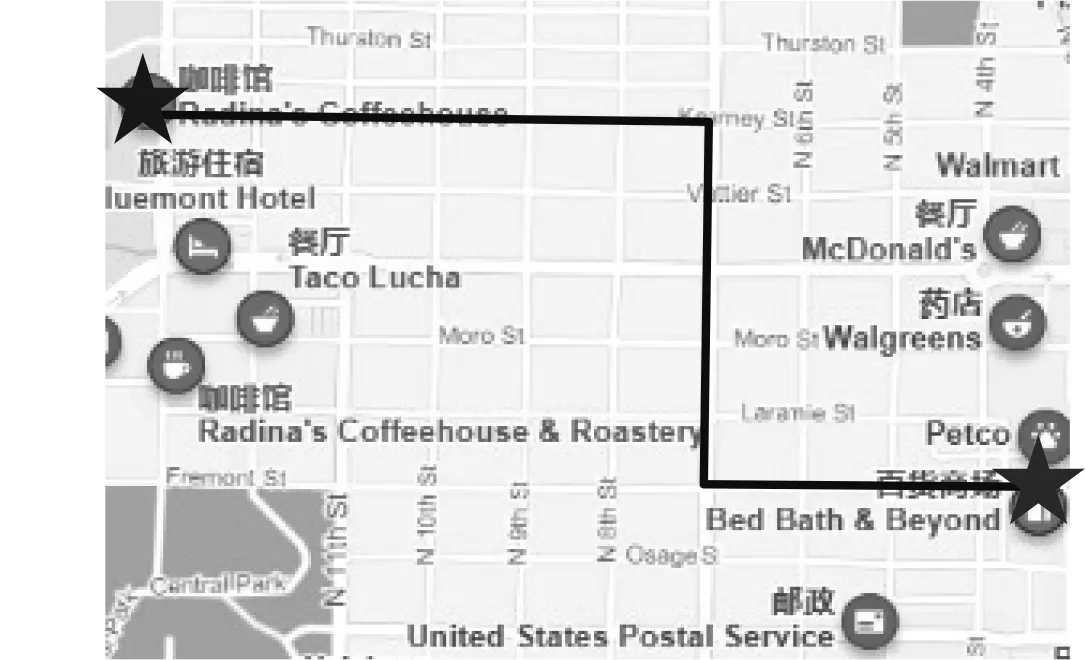
图1 曼哈顿距离在城市 中的应用

在计算机图形学中，屏幕由像素构成，显示的每一个点都在像素上，用坐标的形式描述屏幕上的点，点的坐标也一般是整数．如果直接使用欧氏距离，则必须要进行浮点运算，而浮点运算很慢而且有误差．如果使用曼哈顿距离，则只要进行加减法计算即可，这就大大提高了运算速度和运算精度．

但曼哈顿距离采用了将两点之间的横纵坐标绝对值的差之和作为刻画距离的标准，多个距离间不方便运算，在这一方面，欧氏距离更占优势．

让我们再一次回看问题1，不难发现问题1所提出的距离就是曼哈顿距离，但是它刻画的是点到直线的曼哈顿距离．

类比欧几里得距离，猜测可以将点到直线上点的曼哈顿距离的最小值称为点到直线的曼哈顿距离．

为了便于计算点到直线的曼哈顿距离，我们可以分两种情况进行讨论：(1)对于与x轴夹角小于45°的直线，曼哈顿距离即为过点的竖直直线与原直线相交形成的线段的长度；(2)对于与x轴夹角大于45°的直线，曼哈顿距离即为过点的水平直线与原直线相交形成的线段长度．下面对情况(2)作简要证明．

如图2，已知平面上有点A与直线l，AB平行于x轴，AB与l的夹角α>45°．M为l上除B外任一点，求证：d(A,M)>d(A,B)．

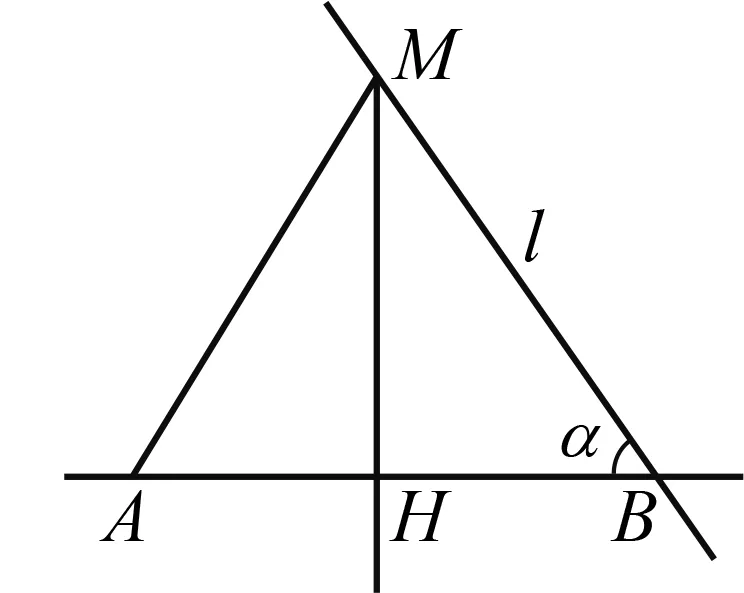
图2

证明d(A,M)=AH+HM，d(A,B)=AB=AH+HB．因为α>45°，所以HM>HB，所以d(A,M)>d(A,B)．

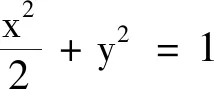
2.3 切比雪夫距离

在R2空间中，A(x1,y1),B(x2,y2)，则A,B两点的切比雪夫距离可表示为d(A,B)=max{|x1-x2|,|y1-y2|}．由切比雪夫距离的定义易证非负性与对称性，下面证明在切比雪夫距离下三角不等式是成立的．

设M(x3,y3)，则d(A,B)=max{|x1-x2|,

|y1-y2|}，d(A,M)=max{|x1-x3|,|y1-y3|}，d(M,B)=max{|x3-x2|,|y3-y2|}，则d(A,M)+d(M,B)≥max{|x1-x3|+ |x3-x2|,|y1-y3|+|y3-y2|}≥max{|x1-x2|,|y1-y2|}=d(A,B)．当且仅当A,B,M共线且M在线段AB上时等号成立．

由上可知，切比雪夫距离满足距离的定义．

对于问题2中的③，本文给出分类讨论的方法．对一般的点到直线的切比雪夫距离进行研究，过程较繁琐，有兴趣的读者可以参阅文[1]．

3 对三种距离的综合理解

3.1 不同距离下的曲线形态

平面直角坐标系中，O为原点．接下来我们通过考虑方程d(O,A)=1所表示的曲线，来研究三种距离的联系与区别．

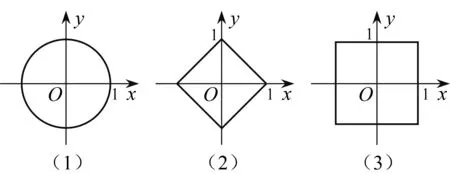
图3 不同距离下的曲线形态

3.2 平面直角坐标系中切比雪夫距离与曼哈顿距离的转化

同为正方形，曼哈顿距离与切比雪夫距离之间是否存在一定的转化关系呢？

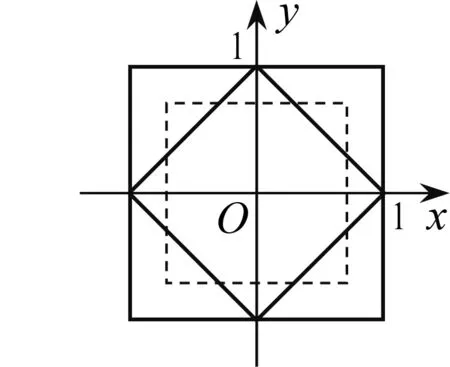
图4 曼哈顿距离与 切比雪夫距离的变换

既然这三个距离之间有许多的性质极其相似，那么是否存在一个通式可以把三种距离统一起来呢？

3.3 闵可夫斯基距离

观察这个式子，我们可以发现：当p=1时得到曼哈顿距离；当p=2时得到欧几里得距离；当p→+∞时得到切比雪夫距离．以下对p→+∞时得到切比雪夫距离进行说明．

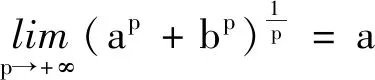
我们生活中随处可见的距离，追根溯源，竟是十分高深的数学原理！上文所讨论的三种距离竟然可以被统一为一个式子．这反映了在众多繁杂的数学概念背后，其实隐藏着的都是相同的本质，就像一棵大树，在外有众多伸向四面八方的枝桠，但最终联系它们的都是同一棵主干，这也体现了数学中万变不离其宗的大道至简之美．