腿式移动着陆器的运动学建模和运动规划
李子岳 郭为忠 韩有承
(上海交通大学机械与动力工程学院 上海 201100)
1 引 言
自航天技术出现以来,对地外星体表面的着陆探测始终是各国深空探测重点关注的内容[1],1959 年至 1976 年间,苏联先后发射了 24 个月球探测器[2],美国的“阿波罗计划”更是实现了人类的首次载人登月,并成功研制了载人月球车[3]。目前,在地外星体表面探测领域,美国处于全球领先地位。除对月球表面的探测外,美国还发射了“勇气号”和“机遇号”轮式火星探测器登陆火星,分析火星岩石和土壤的地质特征,探测水冰和生命活动信息证据[4-6]。在此基础上,美国又发射了第一辆核动力火星车“好奇号”,继续对火星表面进行探查[7]。我国的深空探测虽然起步较晚,但发展稳健,先后在 2013 年和 2018年,实现了“嫦娥三号”和“嫦娥四号”着陆器分别在月球正面和背面成功着陆,搭载的“玉兔号”和“玉兔二号”巡视器实现了对月球表面环境的探测[8-9]。2021 年,“天问一号”着陆器在火星表面成功软着陆,搭载的“祝融号”火星车开展了火表巡查。我国的着陆探测工程以腿式着陆器搭载移动巡视车为主,该着陆器结构刚度高,辅以蜂窝铝等缓冲材料,可较好地完成着陆缓冲任务。纵观国内外所有的腿式着陆器,在软着陆后自身都不具备行走移位功能,发射后巡视探测范围有限。
目前,对四足机器人的运动规划已有较多研究,McGhee 等[10-11]基于静态稳定性系统地证明了四足机器人周期步态的存在性,张帅帅等[12-14]针对开发的 SCalf 液压驱动四足机器人,采用点云建模复杂地形,实现了复杂地形的运动规划。周坤等[15]在稳定判据中采用零力矩点法,通过规划机器人的实时轨迹,使其适应复杂地形。Hwangbo 等[16]利用强化学习方法,使 ANYmal机器人获得超越普通规划方法的运动技巧。此外,并联机构因其承载能力更强,在腿式机器人构型设计中具有优势。马泽润等[17]在地外星体地形中,对一种串并混联的轮腿式机器人的越障能力和运动规划进行了研究。赵辰尧等[18-19]在尺度互异条件下,对腿式移动着陆器的步态规划进行了深入研究,实现了对地外星体复杂地形的规划。Zhao 等[20]开发了 Octopus-III 六足并联机器人,提出一种在复杂地形环境中避障和运动规划方案。Xu 等[21]通过对盲人步行的观察,设计了一套不依赖视觉而通过间接力估计行走的自适应步态。
目前,着陆器着陆后不具备移位能力,但其使用寿命较长,导致一次发射任务不能充分发挥其探测潜力。从长远考虑,开发移动式着陆器十分必要,其兼具缓冲着陆和行走移位功能,在保证结构强度的基础上,还具有灵活性。移动式着陆器在软着陆后作为可移动的母平台,能够搭载巡视器和大型设备从事星体探测活动,形成移动式着陆器加巡视器的探测新模式,拓展仅依靠巡视器进行地面巡视的探测范围。针对移动式着陆器,Lin 等[22]对四足腿式移动着陆器进行了构型设计,使着陆器具有着陆、调姿和行走移位能力。Han 等[23-25]针对腿式移动着陆器的构型、尺度优化和动力学优化等开展建模研究,形成着陆器机构优化设计的方法体系。针对移动式着陆器,本文进行了运动学建模和运动规划方法的研究,丰富了移动式着陆器的相关理论体系。
2 腿式移动着陆器
2.1 着陆器构型与着陆移位一体化功能
本文着陆器为 Han 等[23]研究的 RU&2RUS腿式移动着陆器,本文后续的建模与研究都将基于该构型,部分标号参考该文献相关标号。如图 1 所示,该着陆器的 4 条腿均为 RU&2RUS 并联构型,其静平台与机身固连,动平台与足垫通过 S 副连接。其中,主支链通过转动副和虎克铰与动平台相连,两辅支链从静平台到动平台依次为转动副、虎克铰和球副,3 条支链均设置缓冲器,以减轻着陆冲击对着陆器机构的影响。

图1 RU&2RUS 腿式移动着陆器Fig. 1 RU&2RUS mobile lander
着陆器单腿的构型及各结构参数如图 2 所示。其中,图 2(a)中的蓝色线条表示传动机构,其采用移动副-球副-球副-转动副的空间四连杆结构,黑色部分为执行机构,即上述 RU&2RUS 并联构型。
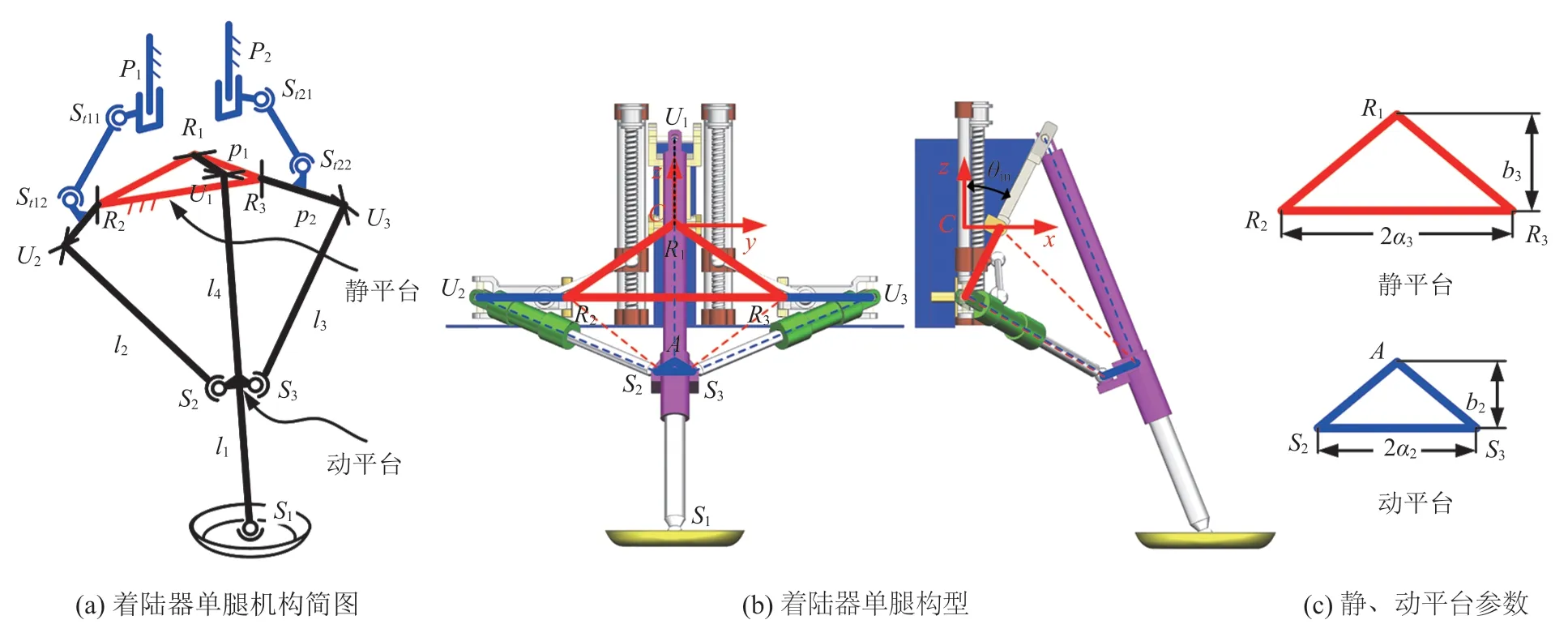
图2 着陆器单腿结构参数Fig. 2 Structure parameters of mobile lander
目前,着陆器只承担缓冲着陆任务,本文所述移动式着陆器在缓冲着陆的基础上,兼具调姿和移位的功能,实现了着陆巡视一体化。着陆巡视一体化任务包含调姿、着陆和行走 3 个阶段。在调姿阶段,着陆器在空中寻找合适的着陆地点,确定着陆地点后在空中悬停,根据地面地形利用着陆器自身搭载的电机对各腿位姿进行调整,调整至着陆模式准备着陆。如图 3 所示,在着陆模式下,3 条支链的 RU 杆均与着陆器机身紧贴。此时整个机构位于边界奇异位形,是为了将着陆缓冲的冲击力传导至机身,避免缓冲着陆带来的冲击力损害传动机构。着陆器调至着陆模式后,在反推发动机的作用下缓缓下降,当到达预定着陆高度后,反推发动机关闭,着陆器在星体重力作用下完成着陆。着陆时,利用着陆模式的特殊位姿和各腿布置的缓冲器,着陆器实现着陆缓冲。着陆完成后,着陆器进入行走模式,各支链的驱动电机启动,从着陆模式调整位姿至行走模式。此时,着陆器转化为并联腿四足机器人,可实现星体表面的四足行走移位,扩大星球探索范围。本文着陆器通过合理的机构设计,在不增加多余结构的基础上,扩充了着陆器的功能,实现了一腿多用。该构型兼具着陆缓冲和行走功能,在满足运动灵活性的前提下,利用合理的机构设计,保护了不耐冲击的电机,为后续的星体表面行走移位创造了条件。

图3 着陆模式和行走模式Fig. 3 Landing and walking configurations
2.2 着陆器单腿运动学建模
建立着陆器单腿的运动学反解模型,是为后续的着陆器运动规划建立数学基础。在本文后续的运动规划和仿真中,足端点均通过着陆器单腿的运动学反解模型与真实样机的关节空间建立联系。图 4 为前述着陆器单腿模型,其中,坐标系C-xyz为固连在机身上的静坐标系,坐标系A-xyz为跟随动平台运动的动坐标系。建立主支链R1U1的 D-H 坐标系如图 4 所示:坐标系R1-xyz的z轴沿转动副R1轴线方向,x轴沿杆R1U1方向,y轴根据右手定则确定;坐标系U1-xyz的x轴沿虎克铰第 2 根转轴方向,y轴沿粉红色套筒方向。根据主支链的坐标系建立动静坐标系间的变换关系如公式(1)所示:

图4 主支链运动学建模Fig. 4 Kinematics modeling of main limb

其中, 为齐次位姿变换矩阵,表示从其左上标关节坐标系到左下标关节坐标系的变换矩阵,各D-H 坐标系的变换关系如下:

在已知足垫坐标的条件下,可以得到主支链的运动学反解如下:


通过求解主支链可得动静坐标系之间的变换关系,利用主支链的求解结果可以对两辅支链进行运动学求解。对左辅支链R2U2S2建立 D-H 坐标系如图 5 所示:坐标系R2-xyz的z轴沿转动副R2轴线方向,x轴沿杆R2U2方向;坐标系U2-xyz的x轴与虎克铰U2的第 2 根转轴重合,y轴沿杆U2S2方向。根据左辅支链R2U2S2的坐标系建立各 D-H 坐标系的变换关系如公式(10)和公式(11)所示:
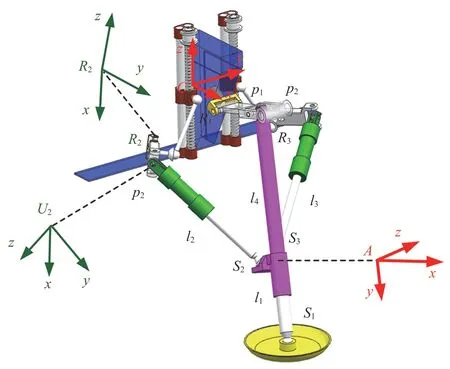
图5 辅支链运动学建模Fig. 5 Kinematics modeling of auxiliary limb

左辅支链满足的几何约束条件为:

将公式(10)、公式(11)代入公式(12),再结合主支链的求解结果,可以得到左辅支链的运动学反解如下:

右辅支链R3U3S3的构型与左辅支链相同,且二者关于主支链对称分布,右辅支链的运动学求解与左辅支链类似,因此,右辅支链的运动学反解如公式(17)~(20)所示。其中, 为转动副的转角; 为虎克铰 第一转轴的转角; 为虎克铰 第二转轴的转角; 为转动副 轴线相对静坐标系z轴的偏角。前述各式中出现的相关点坐标如式(21)所示:

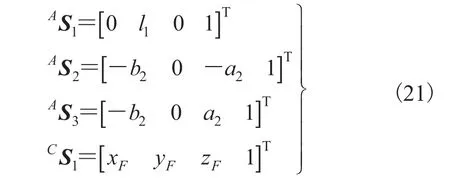
3 着陆器运动规划
3.1 着陆器运动稳定性指标
稳定性是评价足式机器人行走的核心因素之一,合理的评价方式有助于保证机器人的稳定性,因此,必须设置合适的评价指标,用以评价机器人的稳定性。在行走移位阶段,本文所述的腿式着陆器可被视为一种特殊的并联腿四足机器人。在腿的构型和工作空间方面,其与一般的足式机器人有较大区别,需要建立腿式着陆器的静态运动稳定性判断准则,以分析在不同地形条件下的运动稳定性。
稳定性通常采用重心地面投影点(Center of Gravity,COG)/零力矩点(Zero Moment Point,ZMP)判断准则进行描述。如图 6 所示,在重力方向设置新的参考平面,过着陆器的重心向参考平面做垂线,垂足点为 COG。将除摆动腿之外的腿末端触地点围成的多边形定义为支撑多边形。在静态行走的过程中,若 COG 位于支撑多边形内,则认为机器人保持稳定;在非静态行走的过程中,还需要考虑机器人加速度的影响,需保证机器人重力FM和惯性力FI合力方向的投影点 ZMP (图 6)也位于支撑多边形内,其坐标如公式(22)所示[26]:

图6 稳定性指标Fig. 6 Stability index

在静态行走的任意时刻,若不考虑加速度的影响,则着陆器的 COG 应落在支撑多边形内。且为了保证较大的稳定裕度,COG 应尽可能靠近支撑多边形内切圆的圆心。COG 距离支撑多边形的边界越远,稳定裕度越大,着陆器的运动稳定性越高。
3.2 着陆器周期步态
目前,对于传统的四足机器人周期步态已有较多研究,其常用步态为:同侧的两条腿先后迈步,然后另一侧的两条腿依次迈步,该方法被证明具有最大的稳定裕度。但与地球上的一般机器人不同,本文所述着陆器要经受缓冲着陆的巨大冲击,所以着陆器各腿缓冲支链的机构参数会发生较大改变。此时,上述步态不一定具有最大的稳定裕度,需要针对性地计算周期步态腿序。
四足机器人中心投影拓扑图如图 7 所示,在周期步态步序设计中,遍历四足的步序排列,即可计算出所有可行的步序解,遍历方法如下:

图7 四足机器人投影拓扑图Fig. 7 Quadruped robot projection topology map
① 假定迈出腿i,判断其是否符合支撑多边形判断准则,若满足条件,则选择下一条腿进行判断。支撑多边形判断准则如表 1 所示,Kij表示i点与j点(i,j=A,B,C,D)之间的斜率;

表1 支撑多边形判断准则Table 1 Supporting polygon judgment criteria
② 身体最多移动两次,且第一步不能移动身体;
③ 当一种步序搜索完成时,计算当前时刻COG 和四足相对位置,并判断是否与初始时刻相同,若相同,则该步序为一种可行的周期步态腿序;
④ 选取身体移动距离最小的腿序作为周期步态的最优腿序。
采用上述遍历方法即可得到当前各腿尺度条件下的所有可行周期步态腿序,对比选取机身移动距离最小的腿序,即可得到最优步态。
3.3 着陆器自由步态
着陆器的周期步态可以满足大多数平缓地形的移位需求,但星体表面环境复杂,仍需要一套能适应复杂地形环境的自由步态,以保证着陆器拥有足够的移位能力。自由步态没有固定的腿序排列,通常根据地形情况和机器人当前状态选择下一个进入摆动相的腿。在自由步态的研究中,一般以运动学裕度,即沿前进方向的反方向,从落足点到工作空间边缘的距离,作为选择迈步腿的标准。着陆器着陆缓冲后,各腿会出现不同程度的尺度变化[27],各腿的工作空间可能出现尺寸不一的情况。若采用传统方式选择迈步腿,那么机器人可能出现多次选择较小工作空间腿的情况,导致步态不稳定。因此,本文给出一种新的评价指标,即公共工作空间下的运动学裕度,其定义如图 8 所示。以 COG 为原点建立公共工作空间坐标系,对各腿工作空间的落足点进行平移变换如公式(23)所示:
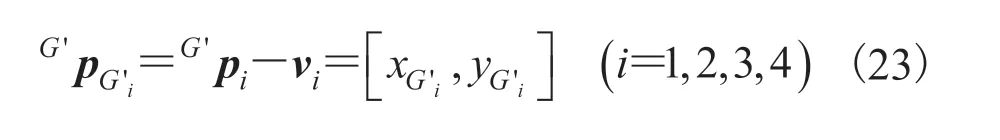

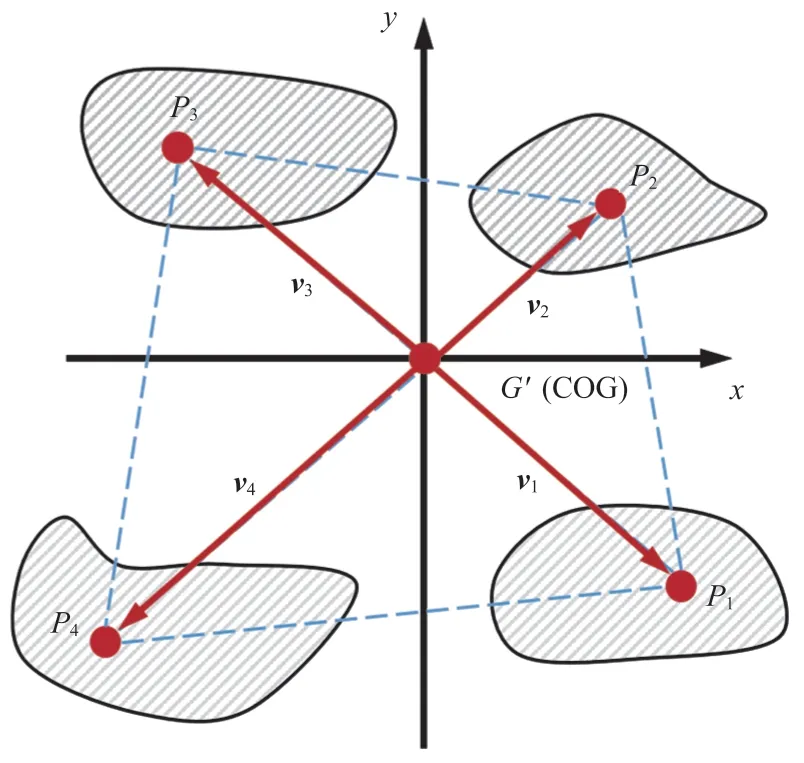
图8 公共工作空间下的运动学裕度Fig. 8 Kinematic margin in public workspace
此外,还需要确定摆动腿的落点,落点需要根据具体的地形条件和单腿的工作空间进行选择,落足点评价函数如公式(24)和公式(25)所示[19]。
其中,u为工作空间内以足端点为起点,括号内变量坐标为终点的向量;Smax为摆动腿在前进方向上的最大步长; 为落足点地形的判断函数,基于该点处的高度、曲率、梯度、周围面积、离障碍物的距离等要素综合判断该点是否可落足,可落足则为 1,反之为 0。基于地形评价函数和着陆器前进方向,公式(24)可筛选出适合落足并尽可能快速前进的落足点。
3.4 着陆器足端轨迹规划
与传统的轮式探测器相比,本文腿式着陆器的显著优点为:在复杂地形中的运动能力较好。前述着陆器的步态规划集中于俯视的二维平面内着陆器身体与四个足端点的运动规划,足端轨迹规划主要关注落足点选定后,足端在空间内的运动轨迹。
为满足着陆器巡视阶段的越障需求,适应不同尺寸、位置的障碍物,足端轨迹在复合摆线轨迹[28]的基础上进行修正,形成了自适应的复合摆线轨迹,表达式如公式(26)所示。其中,S为足端运动的步长;H为足端运动的步高;t为采样时间;T为单次迈步的总时长。引入步长安全系数KS和步高安全系数KH,两系数初始值为 1,根据障碍物的形状、尺寸和位置进行调整,保证轨迹与障碍物无碰撞。该轨迹具有复合摆线轨迹的优势,即轨迹无限阶可导,可保证速度、加速度、冲击的平滑性,还可根据实际情况进行调整,以适应不同障碍物的越障需求。

实际规划时,步长安全系数KS和步高安全系数KH均默认为 1。当着陆器视觉系统检测不到障碍物或前方障碍物尺寸较小时,KS和KH无需调整;当检测到默认轨迹与障碍物发生干涉时,可通过修正KS和KH改变轨迹的形状和位置,使修正后的轨迹完成越障。图 9 为自适应的复合摆线轨迹,其中,红色多边形区域为模拟的障碍物截面,蓝色虚线为步长和步高安全系数为1 的轨迹,黑色轨迹为修正后的轨迹。由图 9 可知,该轨迹可满足着陆器的越障需求。

图9 自适应的复合摆线轨迹Fig. 9 Adaptive compound cycloid trajectory
4 着陆器运动仿真结果
4.1 周期步态仿真
在大多较为平坦的地形中,对于越障和地形评价无过多需求,但周期步态因其具有稳定周期性前进的特点,而具有较大优势。在巡视阶段,将着陆器视为并联腿四足机器人,根据着陆单腿的工作空间可知,其在前进方向上的最大步长为200 mm。假定容许的最小稳定裕度为 10 mm,即COG 到最近的支撑三角形边的距离为 10 mm,根据着陆器整机的情况,给出身体侧摆最大距离为 100 mm,那么使用 MATLAB 编程对周期步态的腿序进行搜索,得到的腿序方案如表 2 所示。其中,单位步长下身体的移动距离为:着陆器在前进方向前进单位距离时,其机身经过距离与单腿迈步距离的比值。由于着陆器机身的运动实际上是 4 条腿的驱动电机共同驱动,因此,从能耗角度考虑,单位步长下身体的移动距离越小,单个周期内的能耗越低,该指标从能耗角度给出了筛选方案的条件。
对表 2 中的周期步态方案 3 进行 MATLAB 仿真验证,如图 10 所示,各图均为着陆器线框的俯视图。其中,各腿标号和 COG 位置已在图中标出,红色虚线连接区域表示此时的支撑区域。由图 10 可知,在整个行走过程中,腿序均符合表中要求,且 COG 始终位于支撑三角形内,满足稳定裕度要求。在整个运动周期内,4 条腿各运动一次,身体移动两次,在垂直于前进方向上的总位移量为 0,保证了周期结束时各腿与机身的相对位置与初始状态相同,而整机在前进方向上移动了 200 mm,形成了稳定的周期步态。

表2 周期步态方案Table 2 Periodic gait

图10 周期步态 MATLAB 仿真Fig. 10 MATLAB simulation of periodic gait
将 MATLAB 周期步态仿真结果与自适应的摆线轨迹相结合,可得到完整的着陆器样机仿真数据,建立着陆器样机整机模型,并导入数据进行仿真,如图 11 所示,仿真结果与理论计算结果一致。

图11 RU&2RUS 着陆器周期步态仿真Fig. 11 Periodic gait simulation of RU&2RUS lander
4.2 崎岖地形中的自由步态仿真
在复杂地形环境中,周期步态不再适用,此时,需要根据视觉系统获取的地形信息进行自由步态规划。根据本文前述的自由步态规划方法,使用 MATLAB 进行编程仿真,如图 12 所示。其中,障碍物的高度和位置是在 MATLAB 中随机生成的,红色虚线表示支撑区域在水平面上的投影。
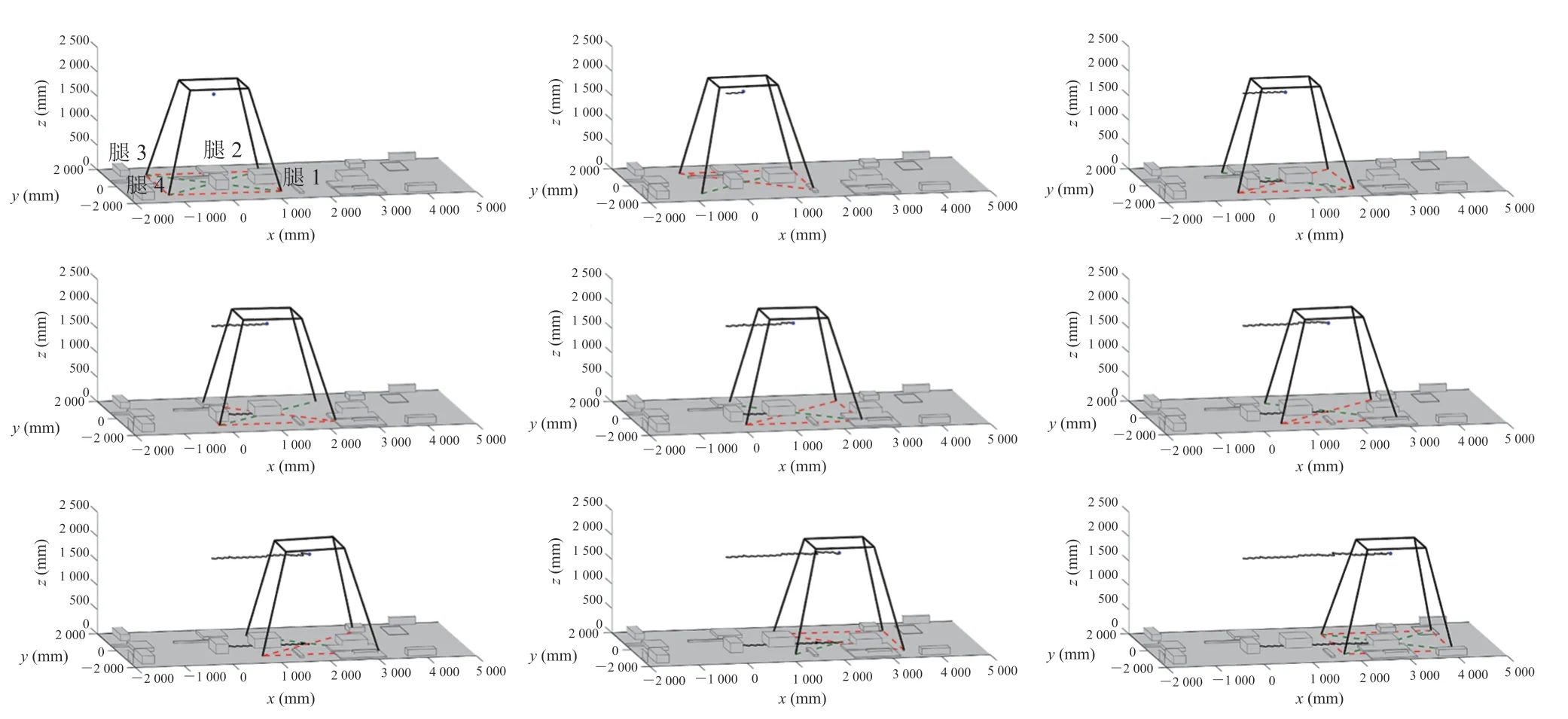
图12 自由步态 MATLAB 仿真Fig. 12 MATLAB simulation of free gait
在整个自由步态的规划过程中,采用身体运动加腿运动的模式,即首先根据当前的位姿和稳定判据,计算出机身质心的位置,进行机身运动,此时各腿均处于支撑相;待机身运动完成后,计算满足稳定裕度条件的腿落足位置,落足位置按照第 3.3 节的方法计算,计算完成后,该腿进入摆动相完成运动。腿的摆动相运动是通过自适应的摆线轨迹实现的,自适应的摆线轨迹可以根据障碍物情况和落足点位置进行参数调节,规划得到连接落足点之间的摆线轨迹。图 13(a)为整个运动过程中着陆器的稳定裕度变化,横坐标为各腿按照运动顺序的摆动相,蓝色虚线为本次规划中设定的稳定裕度下限。由图 13(a)可知,着陆器在整个运动过程中保持稳定,且稳定裕度均不低于设定的下限值。在每一次运动中,着陆器会根据地形信息实时计算足的落点和身体的移动方式,以及根据各腿高低不同来调整机身位姿。图 13(b)为整个运动过程中,机身姿态的调整情况,由图 13(b)可知,着陆器根据地形的变化调整机身的姿态,保证了运动的稳定性。

图13 自由步态稳定裕度与机身姿态变化Fig. 13 Stability margin and body pose of free gait
4.3 讨论与分析
本文提出的改进周期步态和自由步态的规划算法,融合了稳定判据、新的腿序判断方案、公共工作空间下的稳定裕度和自适应的复合摆线轨迹。一方面可以遍历腿序找出当前环境下最适合着陆器的周期步态,以应对平坦地形的同时尽可能降低能耗;另一方面也展示出着陆器的越障能力,通过对落足点、稳定裕度和机身姿态的计算,保证了着陆器通过复杂地形时的稳定性,自适应的复合摆线轨迹也保证了足端不会与障碍物发生碰撞。上述仿真实验通过验证规划算法的功能,证明了该规划算法可以适应复杂地形,保证着陆器流畅稳定地通过崎岖地形。
与 ANYmal 四足机器人的运动规划[29]相比,本文提出的周期步态和自由步态算法更加灵活,可根据着陆器的当前状态和地形环境生成腿序,在面对多变的地形情况时,具有更强的适应能力,但在机身姿态的优化和地形的识别上需要继续改进。与同为并联腿的 Octopus-III[20]相比,在复杂地形的适应性上,本文的规划算法更具优势,可根据机身的当前状态计算最优步序,但本文忽略了大型障碍物的识别和绕行问题。
本文的规划算法均为静步态,每次迈步只有一条腿处于摆动相,满足了着陆器的基本运动需求,后续将会考虑着陆器的动力学过程,进行动步态研究。
5 结 论
针对目前各国普遍采用的着陆器加巡视器的深空星体表面探测模式,本文给出了一种新型的移动腿式着陆器的数学建模和运动规划方法。该着陆器集着陆、调姿、巡视功能于一身,通过调整单腿在着陆和行走模式下的不同位姿,实现了着陆冲击时对驱动电机的保护。基于着陆器运动学模型,本文提出了一套适用于星体表面复杂环境的运动规划方法,即平坦地形中的周期步态和崎岖地形下的自由步态;针对着陆后着陆器可能出现不同姿态和不同腿尺度的情况,本文提出了基于腿序搜索的周期步态腿序遍历方法,该方法可以得到当前条件下的最优步序;针对星体表面复杂的地形,本文提出了公共工作空间下的运动学裕度和落足点判断函数,得到了适用于复杂地形的自由步态规划方法。本文提出的运动规划方法具有通用性,同样可适用于其他四足机器人,对足式机器人运动规划的研究具有潜在价值。

