涌潮作用下弯道丁坝局部冲刷试验研究

钱盛杰，陈 刚，金 新，罗红林，何 昆

（1·海宁市盐仓江堤管理所，浙江 海宁 314423；2·浙江省水利河口研究院（浙江省海洋规划设计研究院），浙江 杭州 310017）

1 引 言

钱塘江河口洪潮水文动力极为复杂，河口的中、上段还伴有涌潮现象，河床冲淤多变，强劲复杂的动力环境条件使海塘基础面临极大的冲刷压力，导致塘脚经常被淘空，危及海塘安全。在海塘工程设计和建设中，通常会修建丁坝以保护海塘，而位于钱塘江弯道的丁坝易受到涌潮冲击，经常发生损毁，屡屡出现险情。

多年来，许多学者对丁坝坝头局部冲刷的过程、深度、防护措施等进行大量研究[1-4]，但弯道三维水流结构和涌潮这一特殊动力条件，共同导致位于弯道的丁坝坝头局部冲刷极为复杂[5-6]。本文采用物理模型对涌潮动力条件下的弯道丁坝局部冲刷进行试验研究，分别用钱塘江河口盐仓弯道整体模型、水槽断面模型模拟弯道段、直道段丁坝的坝头局部冲刷，得到充分防护时涌潮作用下直道段、弯道段典型丁坝坝头局部冲刷经验公式，可供丁坝设计参考。

2 物理模型设计

2.1 整体模型

整体物理模型的上边界设在江东大桥下游约0.8 km处[7]，下边界设在老盐仓大坝下游约5.0 km处，模拟总长约10.4 km，模拟水域面积27.0 km2，平面布置见图1。综合考虑模型场地、模型水流进口过渡段、模型沙选择及研究区域涌潮运动特征，选定整体模型平面比尺λL=200，垂直比尺λh=100，变率η=2的小变率模型。

图1 整体模型平面布置图

为保证水流运动相似，根据相似准数等于同量原则以及潘存鸿等[8]推导建立的涌潮传播速度的解析计算公式，确定整体模型主要相似比尺（见表1）。

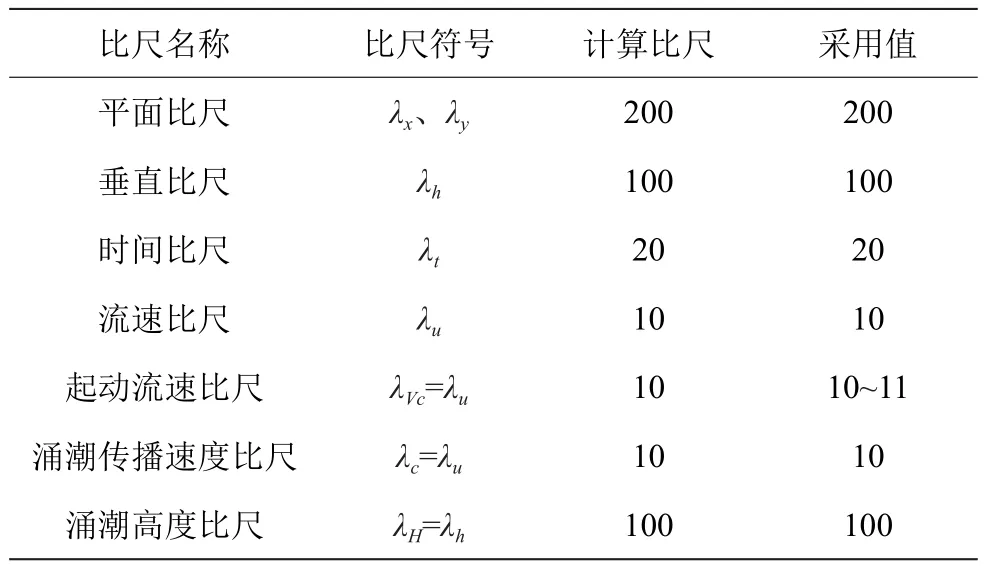
表1 整体模型主要相似比尺表

钱塘江河口河床变形主要取决于悬移质泥沙运动，因此模型为悬移质动床模型，并按起动相似的要求选沙。钱塘江河口的河床质为分选良好、粒径较均匀的粉沙，中值粒径一般为0.02~0.04 mm，分选系数1.7~2.0，泥沙输移以悬沙为主，易冲易淤。经对实测水沙资料进行分析，结合理论公式的计算并考虑研究水域的水深情况等因素，原型沙起动流速0.60~0.90 m/s（水深1~6 m）。根据起动相似的要求，选取中值粒径0.12 mm的木粉作为模型底沙，起动流速为0.06~0.08 m/s（水深5~10 cm），起动相似条件良好。对于坝头抛石的模拟，由于工程区历史上经历过多次除险加固，丁坝坝头及坝身周边抛填了大量厚度不等的抛石、异形块体等，其中抛石质量多为10~100 kg。为遵循起动相似，根据沙莫夫公式、张瑞瑾公式等起动流速公式，选用中值粒径为0.33 mm的原型沙模拟丁坝坝头抛石；对于异形块体，则考虑质量相似。

2.2 水槽断面模型

水槽断面模型采用正态模型，考虑研究区域水流泥沙运动特征与模型沙的特性，选定几何比尺为40，模型长42 m，宽4 m，动床段长10 m，铺沙厚度0.35 m，水槽平面布置见图2。选择中值粒径0.05 mm的木粉作为模型底沙，抛石及异形块体的相似同样分别遵循起动及质量相似。

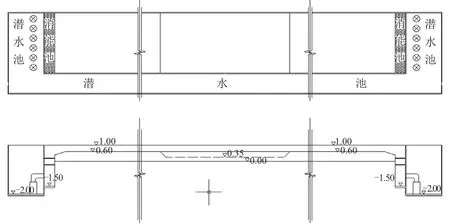
图2 水槽模型平面布置图

2.3 模型验证

模型的水动力验证见参考文献[7]。由于单个涌潮作用下，丁坝冲刷坑的地形实际测量难度极大且精度不高，故整体模型中的动床验证主要以丁坝坝头局部冲刷高程为准。由于在潮汛期内（一般4 d以内）的动力强度相当，从工程安全角度考虑并结合2019年9月的涌潮观测成果，采用实测最大涌潮高度1.7 m左右，8个涌潮的连续模拟，验证盐仓弯道6座典型丁坝的冲刷高程，验证结果见表2。由表2可见，丁坝坝头高程模型验证值与实测值较为吻合。

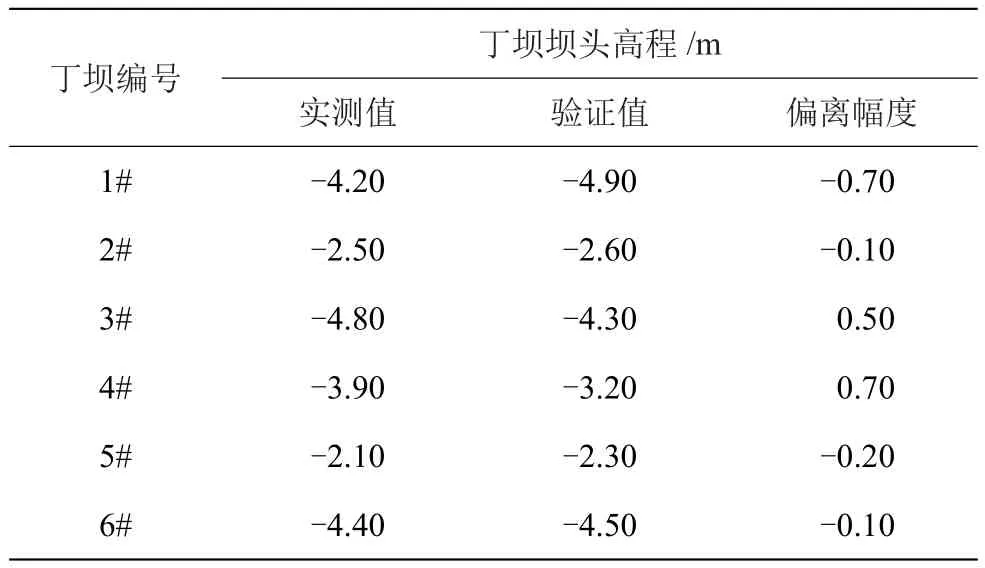
表2 丁坝坝头冲刷高程验证结果表

2.4 试验条件

试验共模拟3种典型丁坝，分别对应2组低丁坝和1组高丁坝，坝长均为80 m，低丁坝的坝顶高程3.60 m，高丁坝的坝顶高程6.60 m，3座丁坝在弯道中的相对位置见图3。

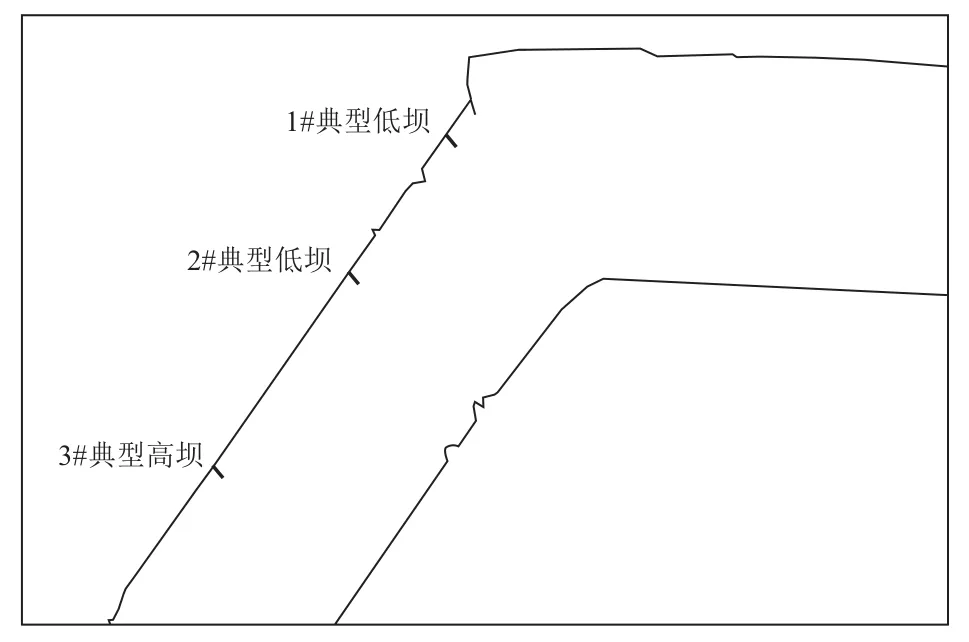
图3 试验丁坝布置图

丁坝试验条件为：起冲高程选择实测较为不利的河床高程1.00 m，低潮位为大潮期的平均低潮位2.4 m，涌潮高度选用2.4 m，试验方案按照不防护—抛石防护—抛石+扭王防护3个渐进方案逐步开展，每个方案实施8个涌潮过程（见表3）。

表3 丁坝试验条件表 单位：m

3 试验结果分析

3.1 丁坝坝头局部冲刷发展过程

丁坝坝头局部冲刷产生的原因非常复杂。普遍认为，由于丁坝的存在，造成丁坝坝头附近水流呈现出强烈的三维紊流特征，改变了周边原有的泥沙动力环境，极大增加泥沙起动机率，加剧丁坝坝头周边河床的冲刷。

丁坝坝头局部冲刷高程随时间发展的过程见图4。通过对丁坝坝头河床高程进行随潮监测可以看出：

（1）不防护条件下，试验初期丁坝附近河床快速下切形成冲刷坑，但随着冲刷的发展，水深增加，流速减小，水流的挟沙能力逐渐下降，冲刷率迅速减小并渐趋稳定。

（2）抛石防护条件下，试验初期丁坝附近河床依旧快速下切形成冲刷坑，但抛石的抗冲能力明显强于泥沙，在2~4个潮后，抛石层即可基本稳定，河床不再明显下切。

（3）抛石+扭王防护条件下，在抛石护底的基础上进一步抛填扭王块压载，以上一阶段抛石稳定后的高程作为起冲高程。由图4可见，随着扭王块的加入，总体上冲刷变缓，初期也无明显河床下切现象。试验中发现，若坑内扭王块紧密摆放，扭王块的滑落或走失数量较少，该高程可认为是丁坝坝头较为不利的冲刷高程。

图4 不同试验方案丁坝坝头局部冲刷发展过程图

3.2 弯道段与直道段丁坝局部冲刷高程差异

整体模型考虑了弯道的影响，其试验成果可反映弯道效应下的丁坝局部冲刷，而水槽模型试验采用断面布置的方式，可近似代表直道段的丁坝冲刷特征，分析2种模型的试验成果差异（见表4）可知：

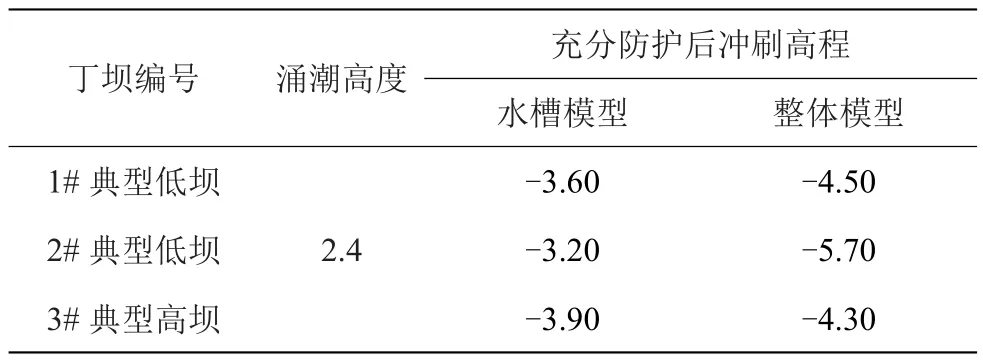
表4 丁坝坝头冲刷高程试验成果表 单位：m

（1）位于弯道中心附近1#典型低坝的坝头冲刷高程，整体模型的冲深较水槽模型加剧0.90 m；而位于弯道出弯后3#典型高坝的坝头冲刷高程，整体模型与水槽模型试验成果相差0.40 m，同样为整体模型略深。表明弯道不同位置的丁坝冲刷，尤其是位于弯道中心附近的丁坝，弯道效应导致其冲刷更甚。钱塘江的实测资料也同样表明[6]，平均而言，凹岸低坝坝头高程较直段顺坝低0.50 m。

（2）试验结果表明，2个模型的2#典型低坝冲刷差异可达2.50 m，远超1#典型低坝和3#典型高坝。结合涌潮传播及强度变化（见图5）可知，由于涌潮传播及行进方向受弯道河岸约束，弯道出弯口2#典型低坝附近水域的涌潮因折返而强度增加，最终导致该区域整体模型的冲刷高程明显更深。

图5 2#典型低坝区域涌潮传播变化图

3.3 坝头冲刷经验公式

钱塘江赭山湾9号潜坝多年实测结果表明，其坝顶高程低至一般低潮位以下1倍涌潮高度，历经数十年始终存在，较易稳定，因此利用弯道段整体模型和直道段水槽模型，可建立丁坝坝头充分防护后的冲刷经验公式：

式（1）中：h为低潮位水深，m；D为丁坝坝头冲刷深度，m；H为涌潮高度，m；KΔ为河势影响因子，本文中弯道段可取2.8~3.3，直道段可取2.3~2.6。

4 结 语

通过物理模型试验对涌潮动力条件下的弯道段、直道段丁坝局部冲刷进行研究，试验结果表明，弯道的丁坝局部冲刷坑较直道段深0.40~2.50 m。冲深加剧主要是由丁坝所处的弯道相对位置这一直接因子，以及受弯道影响所导致的涌潮强度变化这一间接因子共同决定的结果。研究得出充分防护时涌潮作用下直道段、弯道段典型丁坝坝头局部冲刷经验公式，可供丁坝设计参考。