悬浮载荷对无轴承永磁电机电磁力波及电磁噪声影响分析

周晓燕，李德鑫，刘广信

(青岛理工大学 信息与控制工程学院，青岛 266525)

0 引 言

相比于普通永磁电机，无轴承永磁电机具有无摩擦损耗、高转速等优点，在飞轮储能系统、高精密仪器、医疗等领域有较高的应用前景。而气隙磁场的不对称性造成的电磁振动噪声是我们不得不考虑的问题。永磁电机的电磁振动噪声主要是由定转子磁场作用产生的电磁力作用于定子齿引起的，无轴承永磁电机由于其特殊的结构和电磁特性，气隙磁场相较于普通永磁电机更加复杂。

近些年，国内外学者对于永磁电机的振动噪声问题做了很多研究。文献[1]提出了通过合理选择永磁磁极的偏心距来削弱激振力波，以达到削减电磁噪声的目的；文献[2]采用时步有限元法与二维傅里叶分解相结合的方法,获得电机定子内圆处的径向、切向电磁力的频率、阶次和幅值的对应关系，采用动力学有限元法与声场边界元法的非耦合直接计算,对单相电机的振动噪声进行了分析；文献[3]研究分析定子绕组结构、绕组浸漆和绕组端部对电机定子结构固有频率的影响，用于电磁噪声的预测；文献[4]提出了采用转子分段斜极和转子开辅助槽的方法来削弱由低阶齿谐波引起的径向电磁力波,从而削弱该电机的电磁振动和噪声；文献[5]对电机的有、无齿槽结构模型进行两次有限元仿真,得到永磁体磁动势和气隙磁导,对其进行傅里叶分解,即可准确得到包括幅值、频率、相位在内的空载磁动势和气隙磁导表达式；文献[6]提出一种改变磁极结构削弱电磁力谐波的方法；文献[7]提出了有关分布式重叠和单层集中非重叠绕组配置方面的极槽配合来削弱电磁噪声的研究；文献[8]分析并寻找了无轴承电机工作的最佳极数，以产生稳定的磁悬浮，结果表明当使用8个或更多磁极时，径向悬浮力与驱动转矩分离，能够达到理想的效果；文献[9]提出了一种新型的E心无轴承磁通切换永磁电机，以克服转子永磁式无轴承电机的缺点；文献[10] 指出交替极无轴承电机转矩和悬浮力分别正比于转矩电流和悬浮电流、悬浮力与转子旋转角位置无关以及转矩与悬浮控制相解耦等特性，在两者电磁转矩相近的情况下,交替极电机的悬浮力是同样极对数表贴式无轴承电机的2.87倍；文献[11]推导了计及谐波的悬浮力统一公式,指出了不同极对数时,产生悬浮力脉动的情况及原因,并提出了抑制悬浮力脉动的方法；文献[12]提出一种转子磁极离心的磁极形状优化设计方法；文献[13]提出一种基于辅助槽削弱分数槽永磁电机空载激振力波的方法。

以上文献都是研究传统永磁电机振动噪声的问题，针对无轴承永磁电机的研究也大多集中在控制方法等问题，目前对于无轴承永磁电机电磁振动噪声问题还未进行深入研究。

无轴承永磁电机有转矩和悬浮双绕组结构，悬浮绕组的加入使得作用在定子上的电磁力以及电磁噪声更加复杂。本文针对上述问题，以一台8极30槽交替极无轴承永磁电机为样机展开研究。采用解析法推导计算径向电磁力波阶数和对应频率关系，接着建立有限元电机模型，结合有限元法具体计算电磁力波幅值，由此明晰了交替极无轴承永磁电机电磁力波的规律特性。建立了多物理场多转速电磁噪声分析模型，对多种磁场载荷下电磁噪声进行了计算，得出了不同悬浮电流的作用对电磁噪声的影响特点，以及对多转速下电磁噪声的影响特点。

1 电磁力解析分析

为了保证所求电磁力波阶数和频率的正确性，在这里首先采用磁动势-磁导法计算电磁力的阶数和对应的谐波频率，将所得结果与有限元法所求电磁力对比验证。本节所用方法只用于计算电磁力阶数和频率，不用于计算各阶电磁力具体幅值。

图1为一种交替极无轴承电机结构模型示意图。根据麦克斯韦张量法，在忽略磁路饱和及铁心磁阻的情况下，作用在定子铁心内表面的径向电磁力密度(如不加说明所述电磁力均为径向电磁力)可以表示：

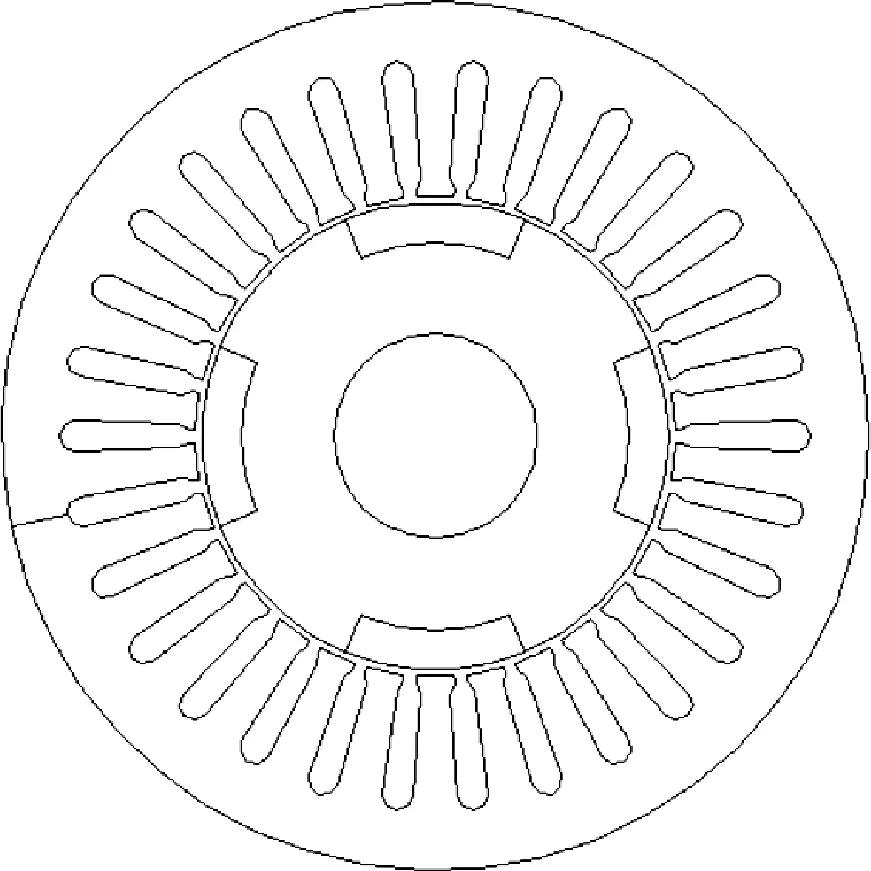
图1 交替极无轴承永磁电机模型

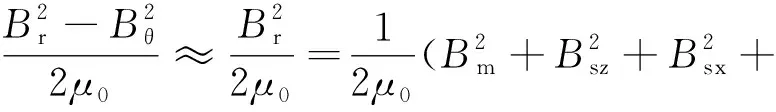
2BmBsz+2BmBsx+2BsxBsz)=

(1)

式中：Br、Bθ分别为径向气隙磁密和切向气隙磁密，切向气隙磁密相比于径向气隙磁密小得多，故忽略切向气隙磁密的影响；μ0为空气磁导率；Bm、Bsz和Bsx分别为永磁体单独作用径向气隙磁密、转矩绕组单独作用径向气隙磁密和悬浮绕组单独作用径向气隙磁密。电机气隙磁密可以表示为磁动势乘气隙磁导的形式。

转子磁动势、转矩绕组磁动势和悬浮绕组磁动势分别表示：

(2)

交替极转子结构的转子磁动势近似呈现如图2所示的分布。转子磁动势表达式如式(2)，其中vm，vsz,vsx如下：

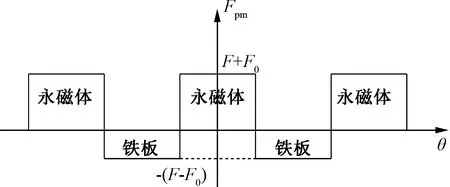
图2 转子磁动势分布

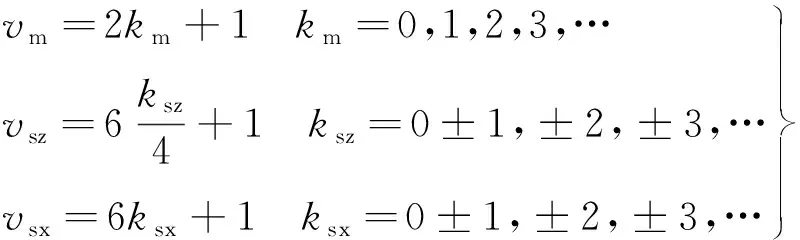
由式(1)和式(2)可得：

(3)

考虑到齿槽的影响将齿槽结构等效成如图3所示的结构。

图3 定子齿槽简化模型

根据图3的定子槽简化模型，电机气隙磁导表示：

Λd=Λ0+∑Λkcos(kQθ)

(4)

由上式可求得：

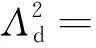
(5)

式中：Q为电机槽数；Λ0为定子无槽平均气隙磁导。将式(5)、式(2)和式(3)代入式(1)并对所求结果归纳整合，可得到电磁力主要频率与阶数对应关系，如表1所示。

表1 电磁力阶数和频率组分

续表1

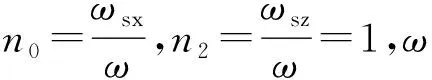
对表1数据总结可知：

1)交替极转子单独作用下电磁力波阶数主要为

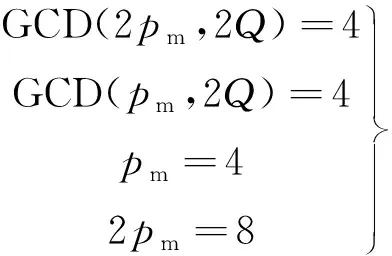
2)转矩绕组单独作用下电磁力波阶数主要为

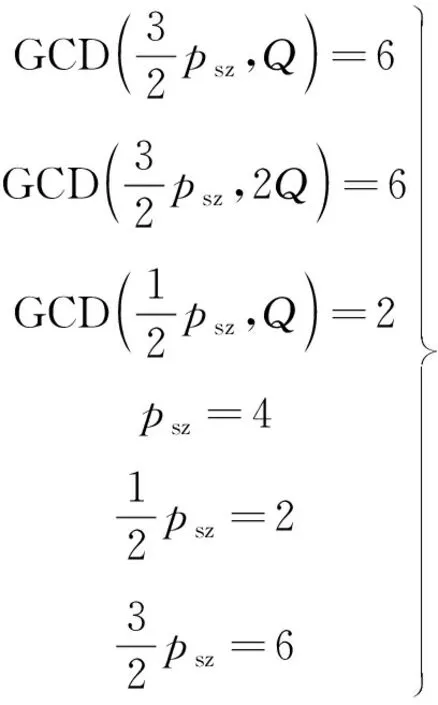
3)悬浮绕组单独作用下电磁力波阶数主要为

4)电磁力的频率包含在[|k|,|2k+1|]2f，其中k=0,±1,±2,±3,…；

5)转矩绕组与转子共同作用下电磁力波阶数主要为

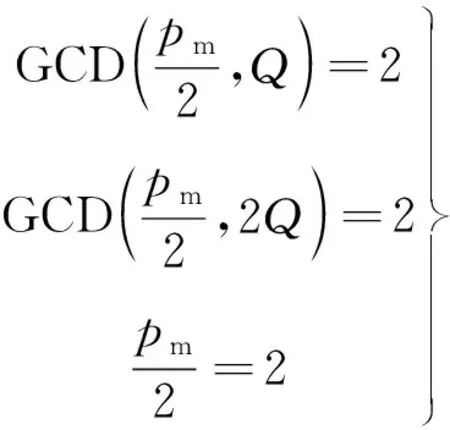
6)悬浮绕组与转子共同作用下电磁力波阶数主要为

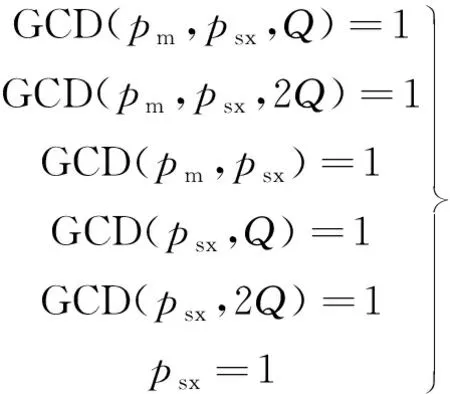
7)悬浮绕组与转矩共同作用下电磁力波阶数主要为

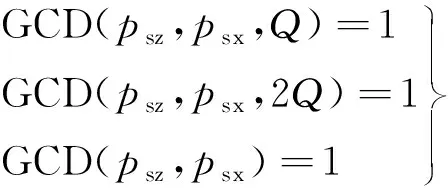
2 电磁力有限元计算

2.1 有限元建模

本文所研究的样机为一台8极30槽的交替极无轴承永磁电机，转子采用表面嵌入永磁体的磁极结构，永磁体处为N极，在永磁体作用下铁极上感应出S极，从而形成一个完整的转子磁场结构。电机定子槽底层为转矩绕组顶层为悬浮绕组。表2为样机的主要参数。

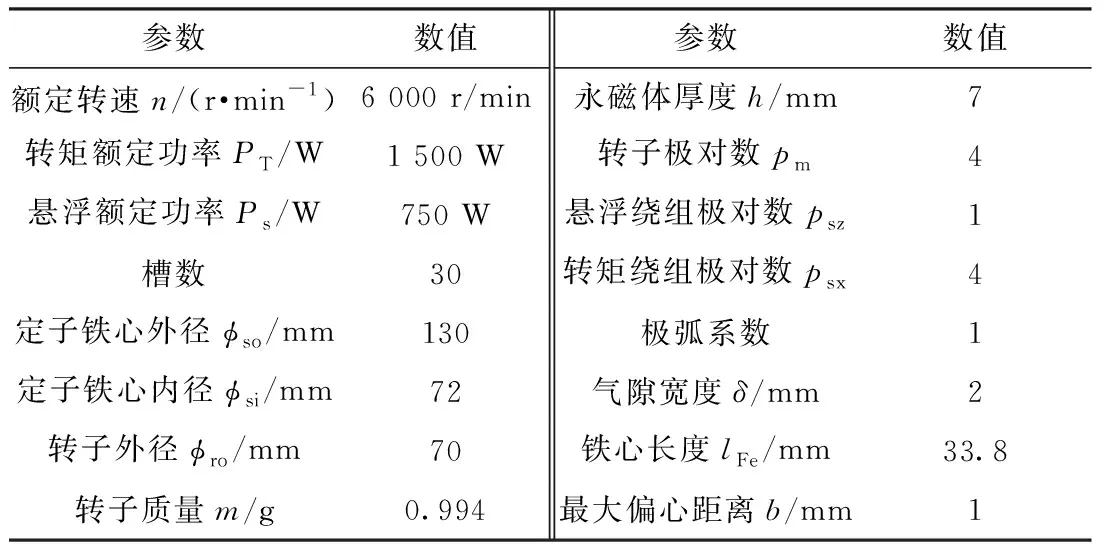
表2 样机主要参数

采用Maxwell建立有限元电机模型，如图4所示，定子槽内层为悬浮绕组，外层为转矩绕组。

图4 有限元电机模型

图5(a)为悬浮磁场单独作用下气隙磁密波形，受到转子铁极部分的影响，悬浮磁场与转子磁场叠加产生了图5(b)所示的畸变磁密。畸变磁密会产生复杂的电磁力谐波，从而影响电机的电磁噪声。切向气隙磁密幅值较小，故忽略对电磁噪声的影响。

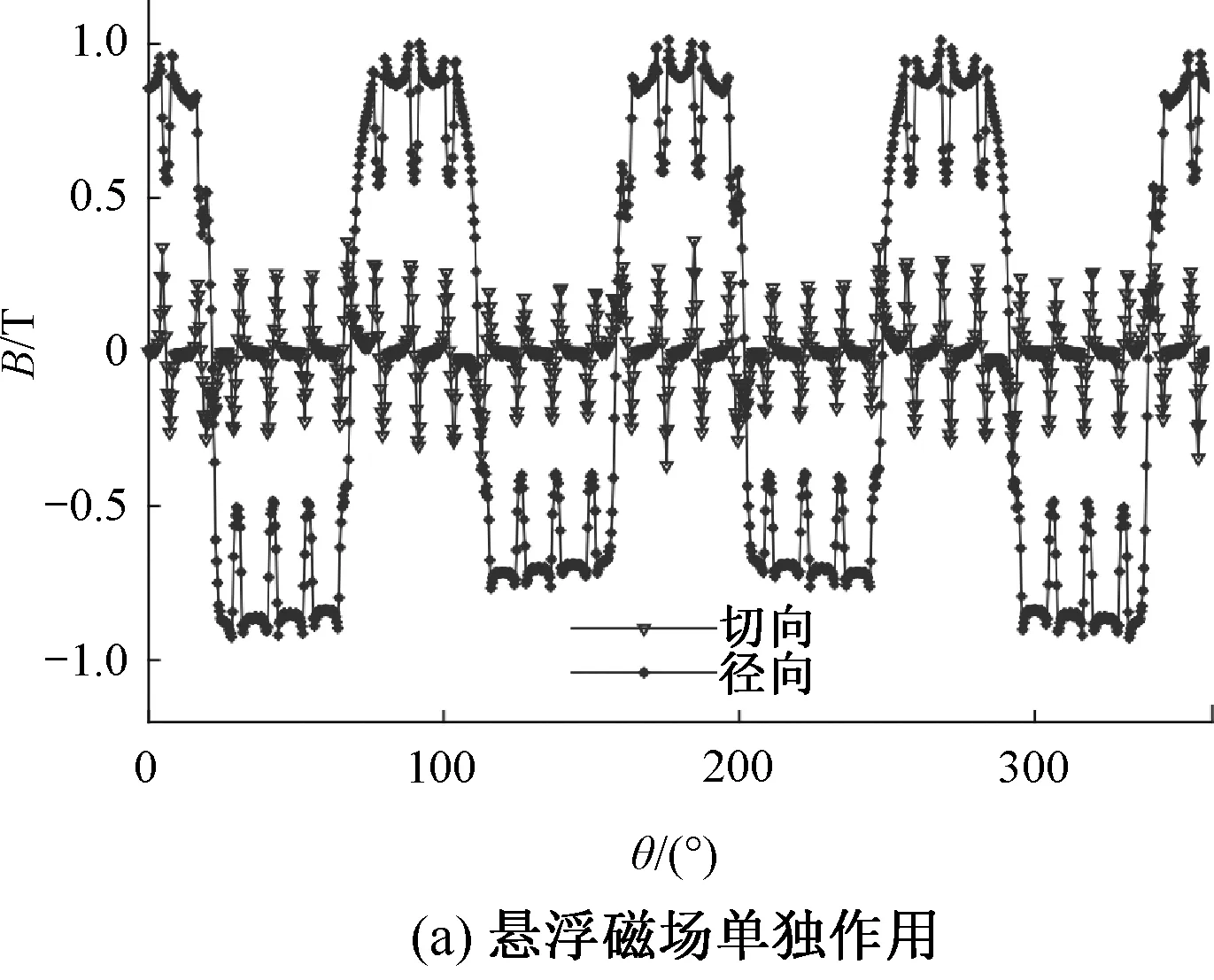
图5 气隙磁密

2.2 电磁力计算

利用上述模型分别计算转矩和悬浮加载时的电磁力，如图6所示。

图6 电磁力波时空分布

图6(a)为转矩电流加载时电磁力时空分布，图6(b)为悬浮电流加载时电磁力时空分布，图6(c)为转矩、悬浮电流同时加载时电磁力时空分布，三种情况下电磁力存在较大差异。图6(d)～图6(f)分别为悬浮绕组单独作用下不同悬浮电流相角和不同幅值下的电磁力分布。综合图6电磁力波形可知，悬浮绕组对电磁力的影响较大。

将图6的时空电磁力进行离散傅里叶分解，为了便于分析，傅里叶分解图中的结果均为谐波幅值的叠加，即将正负阶数下的电磁力幅值按频率叠加统一取正阶数。由文献[6]可知，铁心振动时的动态变形振幅近似与施加的力波阶数的4次方成反比，阶数越高对电磁振动噪声的影响越小。本文选择前13阶力波展开分析。

图7(a)为空载条件下电磁力波傅里叶分解结果。由图7(a)可知，电磁力波主要有4、8、12等阶次，它们满足转子磁场作用下分析的电磁力阶数关系，同时各次力波的谐波频率也满足表1中的频率特点，为基波频率的整数倍。

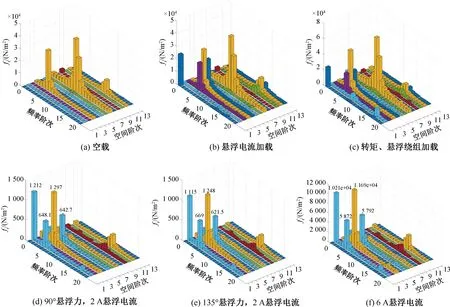
图7 二维傅里叶分解

图7(b)为悬浮电流加载时电磁力傅里叶分解结果。除了存在4、8、12等阶次外还增加了1、3、5等奇次力波，满足转子磁场与悬浮磁场共同作用下分析的电磁力阶数关系，对应的频率主要为0、400 Hz等，同样满足表1频率特点。

图7(c)为两套绕组电流同时加载时电磁力傅里叶分解结果。电磁力波主要有1、2、3、4、5、等阶次，同样满足上述电磁力阶数关系，频率也满足特点；由于转矩绕组产生的阶数与永磁体相同，图7(c)中2，4，6等阶数电磁力幅值高于图7(a)中对应阶数的幅值。

电机控制时，通过改变悬浮电流的相位从而改变悬浮力的方向[15]，图7(d)和图7(e)分别为产生90°和135°两方向悬浮力时，加载2 A悬浮电流单独作用下的电磁力波傅里叶分解结果。电磁力阶数主要为2、4、6、8等阶数，满足GCD(2psx,Q)=2的整数倍关系，同时频率也满足表1特点。从上述两图可知，悬浮电流的相位影响电磁力波的幅值大小。

图7(f)为6 A悬浮电流作用下电磁力分解结果，悬浮电流越大，电磁力幅值也越大。

上述计算明晰了此款电机电磁力波的特点，为后续的电磁噪声分析奠定了理论基础。

3 电磁噪声计算

3.1 模态分析

为了提高计算速度，采用模态叠加法计算电磁噪声，对准确计算定子结构的固有模态频率提出了较高的要求。考虑到电磁噪声计算的准确性，本文借助Workbench耦合谐波多物理场响分析电磁噪声，充分考虑定子上复杂的齿槽结构，所得的数值解具有较高的准确度。

这里所考虑的定子组件包括定子铁心(将机壳与定子铁心等效为一体)和绕组；定子铁心和绕组均非实体结构，而在有限元等效模型中采用了实体结构，必须将实体赋予各向异性材料参数，如表3所示，来体现层叠结构的影响[16]。

表3 定子组件各向异性材料参数

定子组合结构等效如图8所示。

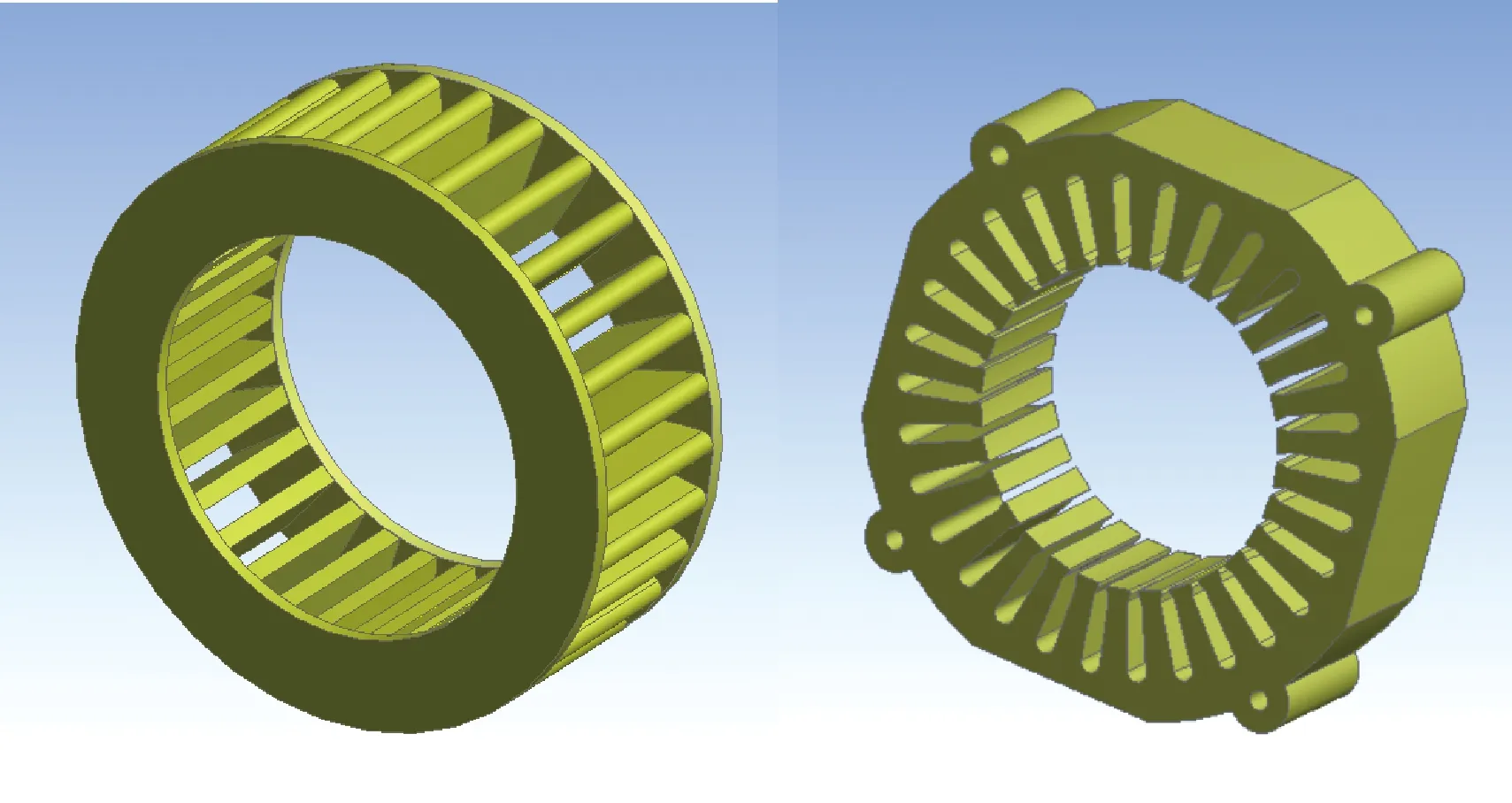
图8 定子组件等效结构图

基于图8的等效结构和表3的材料参数展开模态计算。电机定子齿振型有齿对称和反对称两种。齿对称用s表示，反对称用r表示。为了更贴近实际，模态分析需添加4个角的固定约束条件，定子模态如图9所示，定子组件固有频率如表4所示。

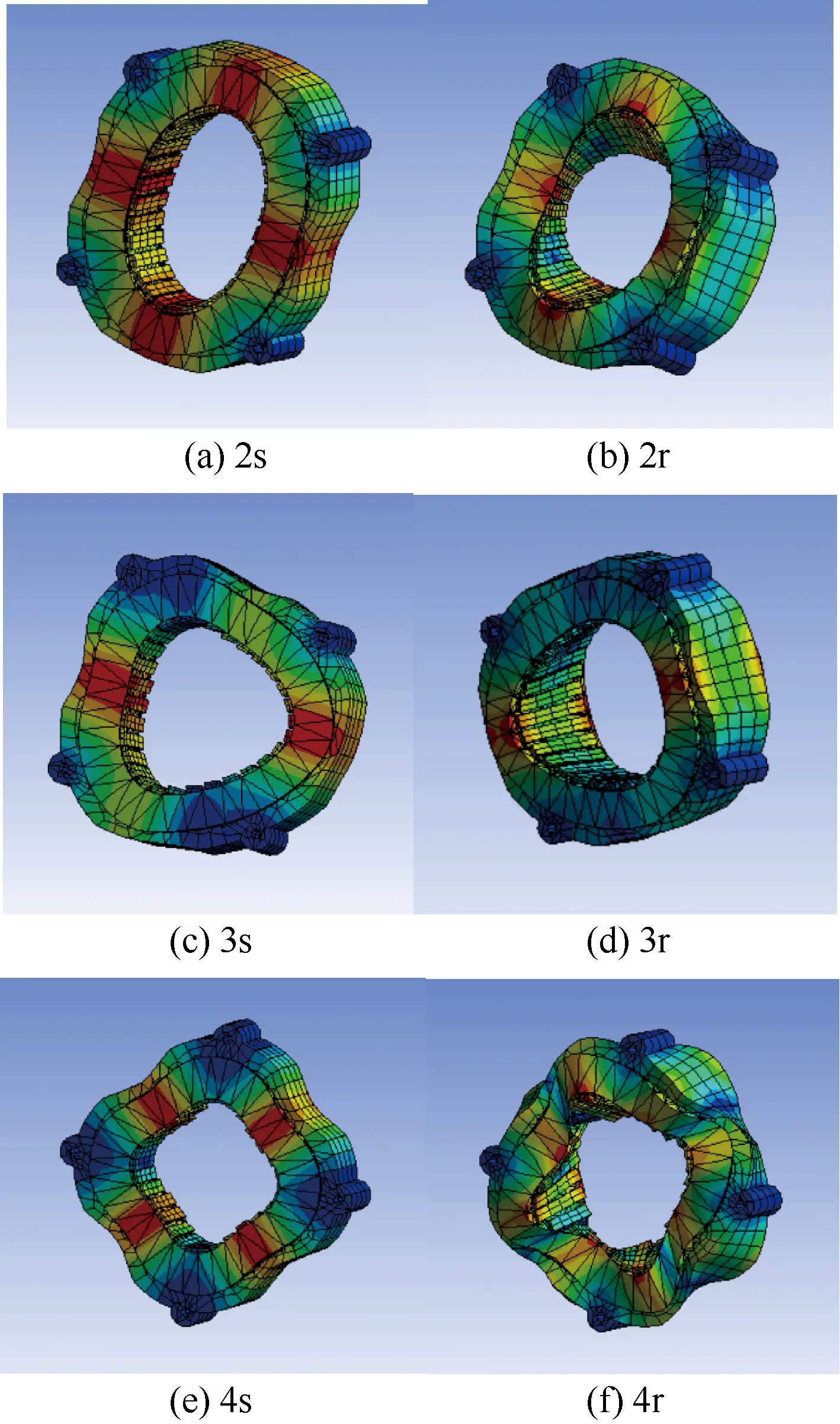
图9 定子模态

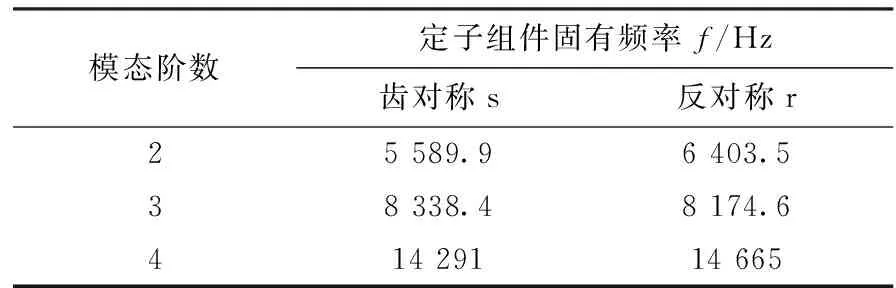
表4 定子组件固有模态频率

3.2 噪声特性分析

当假设定子无槽时，将电磁力密度幅值为pnr的nr阶电磁力施加在定子铁心组件内表面，采用等效集中力作用时，等效力：

Pne=2πrlpnr

(6)

式中：r为定子铁心内半径，r=36×10-3m;l为定子轴向长度，l=33.8×10-3m。

实际情况中定子内壁是定子齿与定子槽的组合结构。相关研究表明，电磁力主要作用在定子齿上，这里将所求各阶电磁力施加到定子齿上，因此需要对定子齿结构做出计算，如下为计算过程。

图10(a)中槽口宽度lBs0=2×10-3m，则可确定一个定子齿所占的圆周角：

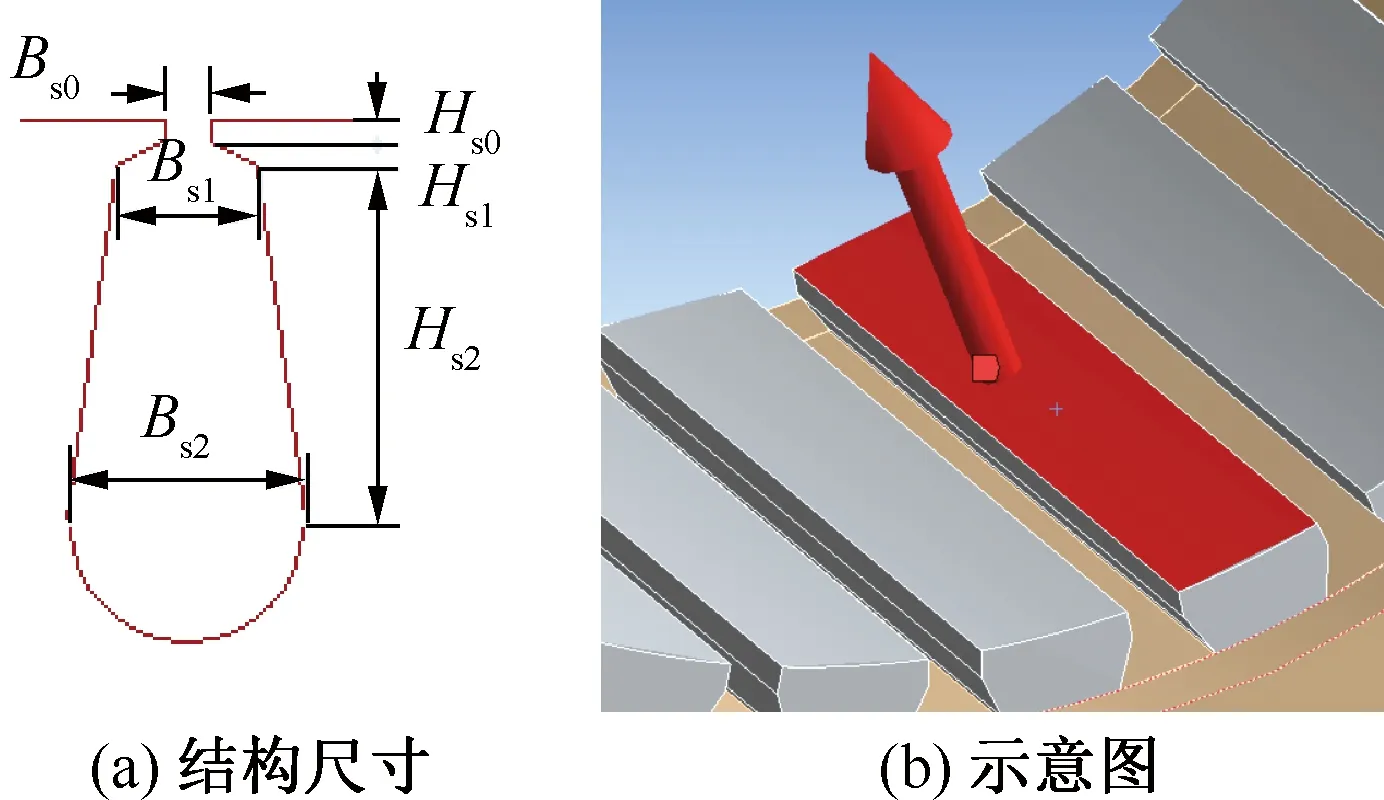
图10 齿槽结构

(7)

式中：Q为槽数。一个定子齿所占的面积：

(8)

则可以推导出一个定子上施加的等效集中力：

(9)

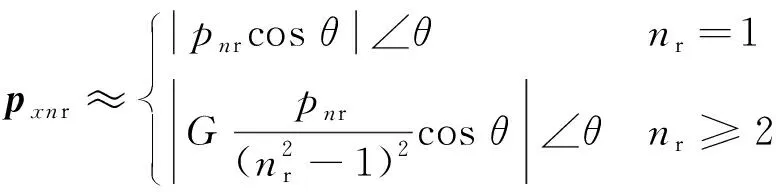
θ为某一个定子齿的空间位置角，G为比例系数。将等效叠加集中力分别施加于不同的定子齿上，从而促使定子组件发生形变产生振动，向外辐射噪声。所求得的电磁噪声响应如图11、图12所示。

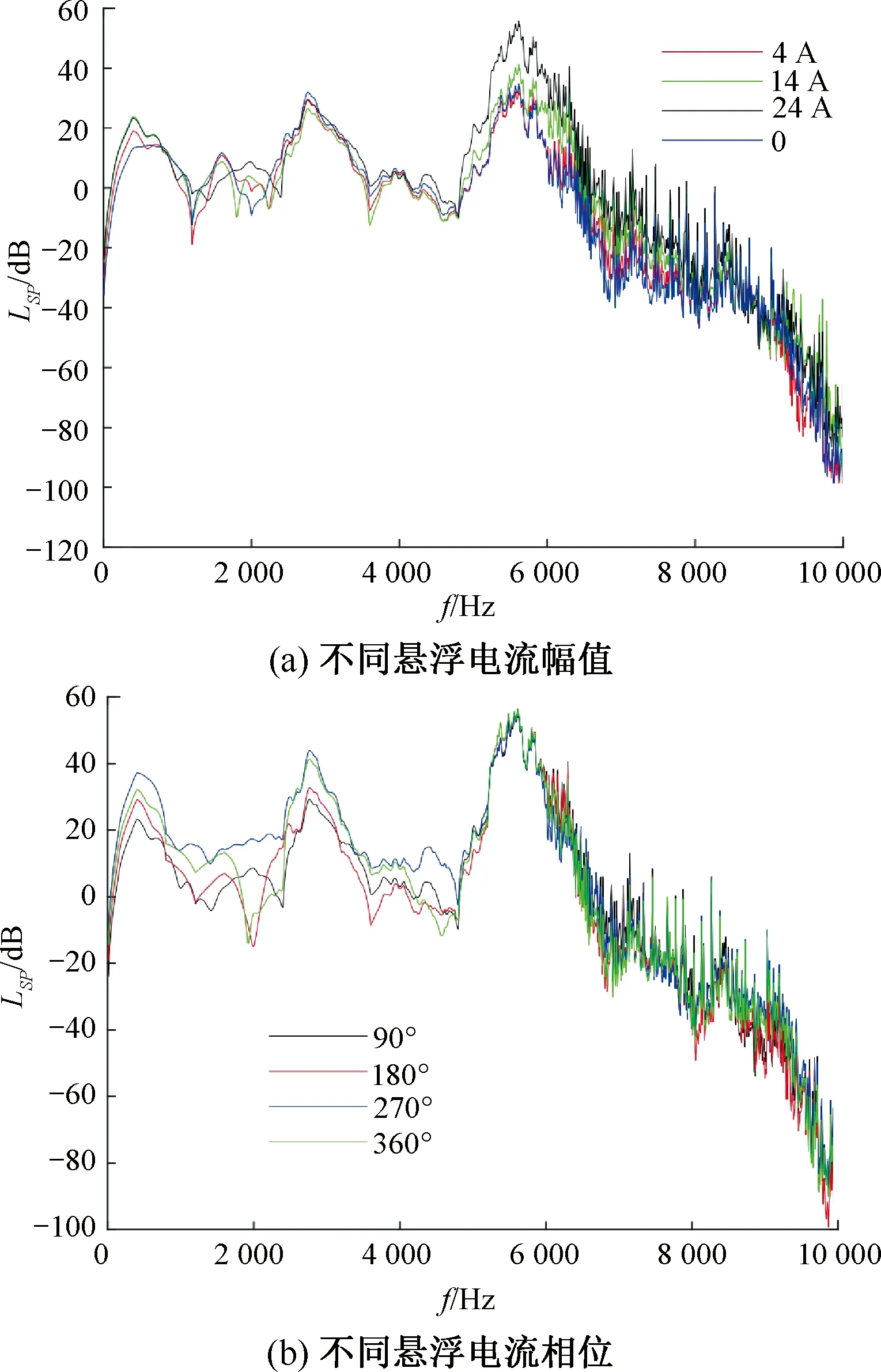
图11 声功率级频谱

图12 多转速声功率级云图

图11(a)为不同悬浮电流幅值下的电磁噪声频率响应，图11(b)为不同悬浮电流相位下的电磁噪声频率响应。由结果可知，增加悬浮电流的幅值会增加5 000～8 000 Hz频段的电磁噪声，而改变悬浮电流的相位，对0～5 000 Hz频段的电磁噪声影响较大。

图12为悬浮电流作用下5 000～15 000 r/min转速范围的电磁噪声响应。在333.33～8 000 Hz频率范围内噪声较大,在上述转速范围内噪声峰值随着频率的增加先增大后减小，在11 667 r/min转速下噪声峰值达到最大85.138 dB(A)，每个转速下的峰值噪声对应的频率随转速增加而增加。

4 结 语

针对交替极无轴承电机电磁噪声问题，本文将解析法与有限元法相结合，完整地分析了电磁力波幅值、阶数和频率的特点。根据多物理场多转速电磁噪声分析模型来计算电磁噪声，得出了不同悬浮电流幅值和相位影响下的电磁噪声变化特点，以及悬浮绕组作用下多转速下电磁噪声的分布特点。具体如下：

1)空载状态下电磁力波主要为4、8等阶次，转矩加载会增加2、6等阶次，悬浮加载会增加1、3等阶次力波；对应的频率主要为0、1 600 Hz、2 000 Hz、3 200 Hz、3 600 Hz等。

2)悬浮电流的幅值变化主要影响5 000～8 000 Hz频段的电磁噪声；而改变悬浮电流的相位主要影响0～5 000 Hz频段的电磁噪声。

3)悬浮电流作用下，电机在333.33～8 000 Hz频率范围内噪声较大,在5 000～15 000 r/min转速范围内噪声峰值随着频率的增加先增大后减小,在11 667 r/min转速下噪声峰值达到最大85.138dB(A)，每个转速下的峰值噪声对应的频率随转速增加而增加。