自寻优最大转矩电流比矢量控制连载之四:同步磁阻电机同构电感建模的虚拟信号注入法控制
张雨馨,王云冲,2,史 丹,徐彬涵,沈建新,3
(1.浙江大学 电气工程学院,杭州 310027;2.浙江省电机系统智能控制与变流技术重点实验室,杭州 310027; 3.流体动力与机电系统国家重点实验室,杭州 310027)
0 引 言
同步磁阻电机(以下简称SynRM)在基速以下通常采用最大转矩电流比(以下简称MTPA)控制。传统的公式法将SynRM中的电感参数等视为常数[1-2],认为电流矢量相位角为45°时的工作点即为MTPA点。实际上,受到磁路饱和效应、磁链耦合和温度等影响,SynRM的参数是非线性变化的[3-4],将电机参数视为常数的MTPA控制算法势必带来误差。考虑SynRM参数非线性变化带来的问题,学者们提出了许多解决方案。主要分为离线法[5-7]和在线法[8-20]。
虚拟信号注入法(以下简称VSIM)[17-20]是一种应用较广的在线法。通过计算虚拟的高频电流矢量相位角偏差信号注入前后的转矩差值,实现电流相位的动态自寻优。但由于VSIM模型依赖d轴电感参数,而电感参数是时变的、无法准确预知的,因此在电机进入饱和区工作时稳态精度会下降。另一方面,由于VSIM没有真实注入信号,不会引入额外损耗,同时具有真实信号注入法计算简便、动态响应快等的优点,成为近年来的研究热点。
考虑到SynRM的参数是非线性时变的,本文在虚拟方波注入法MTPA控制的基础上对于具有饱和效应的SynRM的转矩曲线进行了分析,提出同构电感的概念,并证明基于同构电感的控制模型与被控电机有等效的最优电流相位角。在此基础上,本文设计了相位摇摆法来辨识同构电感。相比于对转矩模型中电感参数进行遍历扫描搜索的方法,采用同构电感概念可以更方便计算出MTPA工作点。最后,本文通过仿真与实验,验证了本方法可有效弥补电感参数时变带来的寻优误差,能够在SynRM上取得较好的控制效果。
1 SynRM模型及非线性变化特性
三相SynRM在d-q参考坐标系下的模型可以表述:
(1)
(2)
(3)
(4)
iq=Iscosβ
(5)
id=-Issinβ
(6)
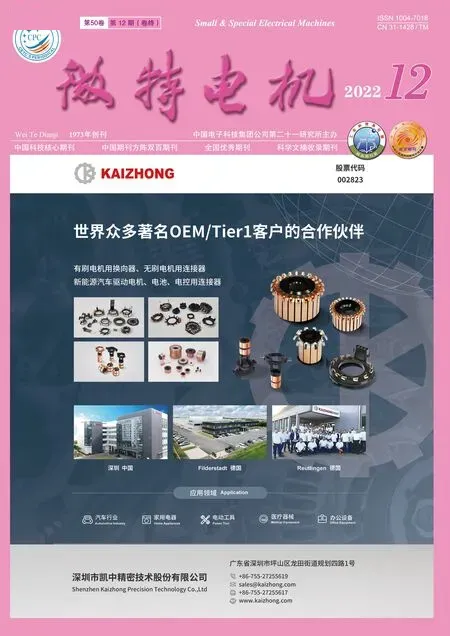
式中:vd,vq分别为d,q轴电压;id,iq分别为d,q轴定子电流;Ld,Lq分别为d,q轴电感;R为定子电阻;Te,TL分别为电磁转矩和负载转矩;ωm为转子的机械角速度;p为电机极对数;Bm为摩擦系数;J为转动惯量;Is为电流矢量的幅值;β为电流矢量超前q轴的相位角。
温度、磁路饱和效应等会使SynRM的电感参数发生非线性变化。具体表现如下:
1) 电流的磁效应会对SynRM的磁路特性产生非线性影响。运行中定子电流会导致铁心磁路发生非线性的饱和,同时d,q轴电感之间存在交叉耦合,使得d,q轴电流会引起电机d,q轴电感发生显著的非线性变化[21-22]。图1展示了SynRMd,q轴电感随电流的变化规律。可以看到,q轴电感的非线性变化很明显;当id,iq较小时,d轴电感也有显著的非线性变化;并且这种非线性变化难以用数学方法建模,使得考虑电机参数非线性变化的MTPA精准控制变得困难;

图1 SynRM d, q轴电感随电流变化
2) 温度变化也会导致导磁材料的磁导率发生变化[23],从而对SynRM电感参数产生影响,进而影响MTPA控制。
2 基于VSIM的MTPA控制

(7)
式中:N=1,2,3,…;δ和Ts分别表示方波信号的幅值和周期。对注入虚拟方波信号后的转矩进行泰勒展开及忽略二阶及以上导数项,可得:
(8)

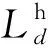
(9)
(10)
传统VSIM在计算过程中将电感参数Ld和Lq视为常数(当然,只是在一个虚拟信号注入周期内视作常数,而非全局视作常数),忽略了SynRM参数的非线性特性,这会降低算法的MTPA控制精度。
值得注意的是,现有的关于VSIM研究大多应用于PMSM,PMSM以永磁体产生的电磁转矩为主,永磁体产生的偏置磁场使得磁路接近饱和状态,电机电感受电流影响相对较小,电感的非线性特性不明显,因此VSIM在PMSM上能取得较好的MTPA控制效果。SynRM转子没有永磁体,其转矩主要为d,q轴电感差导致的磁阻转矩,它的磁路饱和状态完全由电流决定,使得SynRM参数非线性变化十分显著[24]。采用传统的VSIM对SynRM进行控制会产生较大误差,无法实现高精度的MTPA控制效果。
本文考虑SynRM参数的非线性特性,提出同构电感的概念,在传统VSIM的基础上构建基于同构电感的转矩模型,提高模型的准确性,从而改进MTPA控制的精确性。
3 基于同构电感模型的VSIM
3.1 基于同构电感的转矩模型重建
考虑SynRM参数随d,q轴电流变化而非线性变化的特性,注入信号后的期望转矩计算表达式:
(11)
通过添加数学等价的配凑项,重写:

(12)
考虑到当电机运行在稳态下有如下关系:
vq-Riq=pmLd(id,iq)id
(13)
vd-Rid=-pωmLq(id,iq)iq
(14)
转矩表达式可进一步重写:

(15)
式中:
(16)
(17)
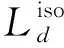

图2 采用同构电感转矩模型的MTPA工作点
3.2 用于同构电感辨识的相位摇摆法
1) 算法启动,初始化同构电感值为零值;
2) 在当前同构电感值下使用虚拟信号注入法MTPA收敛至稳定,获取前驱电压方程:
vd=Rid-pωmLq(id,iq)iq
(18)
vq=Riq+pωmLd(id,iq)id
(19)
3) 冻结虚拟信号注入法模块,将当前的电流相位角偏移增量角,待电机再次进入稳定状态,获取后驱电压方程:
(20)
(21)
4) 基于两组电压方程可计算得到更新后的同构电感参数,其中d,q轴同构电感可表示:
(22)
(23)
5) 将电流相位角折减去先前叠加的偏移角,并重新唤醒虚拟信号注入法模块,使其基于更新之后的同构电感模型进行MTPA工作点寻优;
6) 重复步骤2)到步骤5)直至系统收敛至稳定。
3.3 相位摇摆法的自启动机制
相位摇摆法可以有效观测辨识同构电感,但不具备自启动机制,在外界工况改变时不能及时更新同构电感,将导致寻优出错,无法实现控制效果。本文提出利用均势电感以监测系统工况变动的办法。均势电感定义为同时满足相位摇摆法的前驱电压方程和后驱电压方程的参数:
(24)
(25)
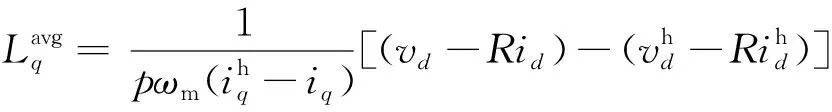
(26)
考虑到相位摇摆法中偏移的角度很小,针对d轴电流有如下关系式:
(28)
从而有:
(29)
可以看到,d轴均势电感值与计算的d轴同构电感有相同的表达式。引入均势电感后,对相位摇摆法的自启动机制可进行如下优化:每个控制周期内,根据采样的电流值和转速,基于当前均势电感计算预估电压,并比对预估电压与当前采样电压值,若两者误差在设定的阈值内,可认为电机的工况未出现大变动;若比对误差较大,说明电机的工况发生明显的改变,前一轮确定的均势电感和同构电感均已失效,需重新执行相位摇摆法,以确定新工况下的均势参数和同构电感值。
由上述原理分析可知,虚拟双极性方波注入法属于不考虑参数非线性变化的传统VSIM方法,但相比于虚拟单极性注入法有更高的稳态精度。本文在虚拟双极性方波注入法的基础上采用相位摇摆法,辨识出同构电感,并重构转矩模型,由此改进VSIM控制。系统控制框图如图3所示。
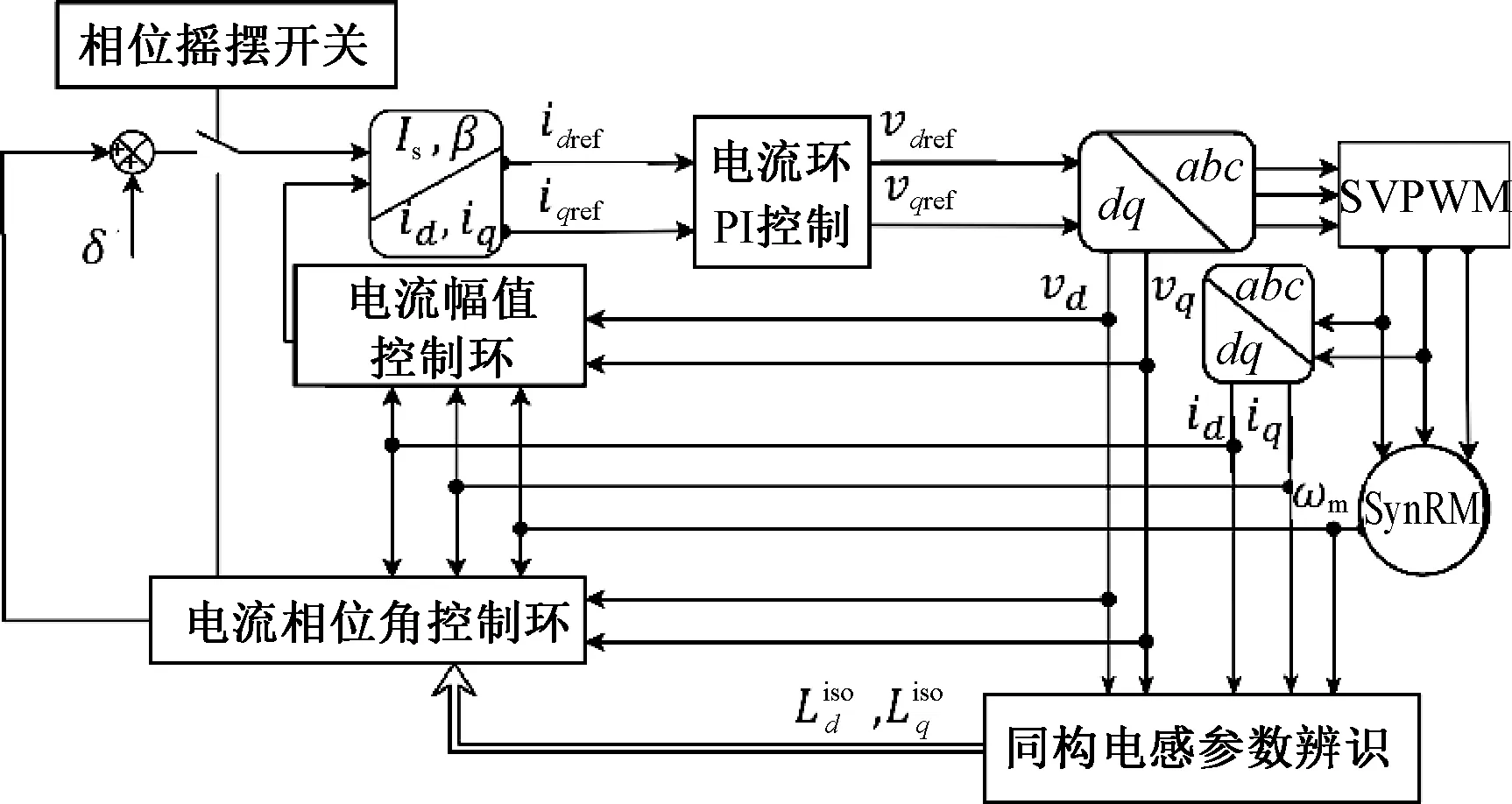
图3 系统控制框图
4 仿真分析
为对算法的可行性进行验证,本文首先对基于同构电感转矩模型的VSIM进行仿真分析。仿真考虑了SynRM电感参数的非线性特性,在Simulink中搭建的SynRM模型电感参数与实际被控制电机的有限元仿真结果一致,通过查表获得。电机参数如表1所示。
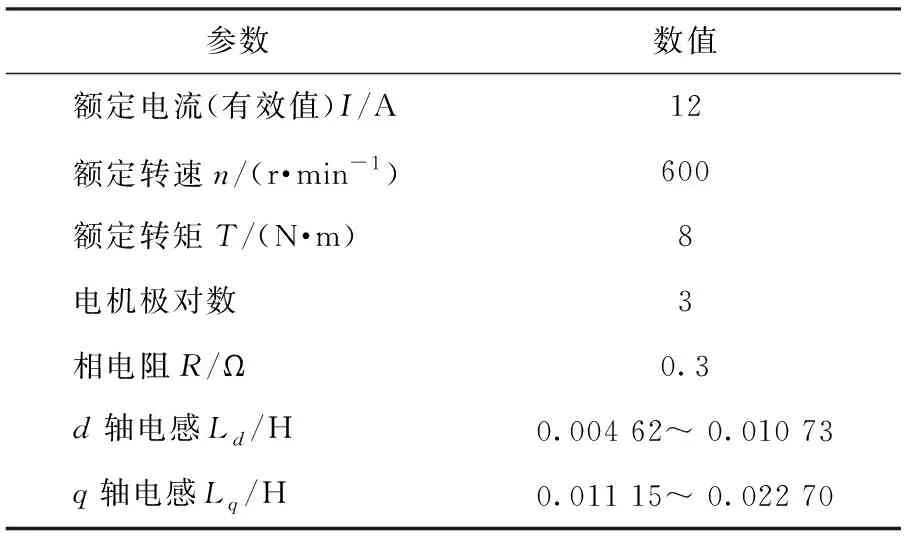
表1 SynRM参数
4.1 稳态性能研究
将基于同构电感转矩模型的虚拟双极性信号注入法与虚拟单极性方波信号注入法控制下的电机稳态电流幅值进行对比,如表2所示。给定电机转速600 r/min,给定负载转矩分别为2 N·m、4 N·m、6 N·m、8 N·m,当电机稳定运行后,取仿真最后1 s内电流幅值的平均值为结果。
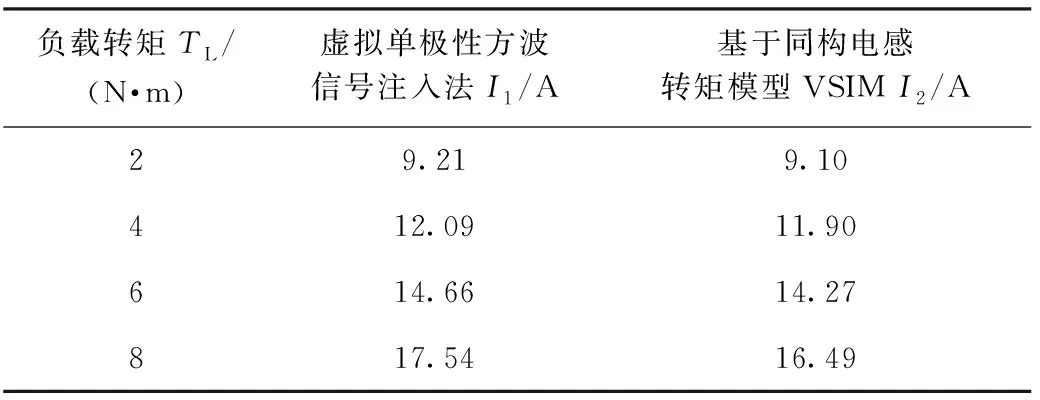
表2 600 r/min下的SynRM稳态电流值仿真结果
从表2可以看出,由于考虑了SynRM非线性特性,重新构建基于同构电感参数的转矩模型,本方法控制下的电机在各个给定工况下的稳态电流值更小。这是因为补偿了传统VSIM将电机电感参数视为常数的误差,提升了MTPA控制的稳态精度。
同时我们观察了电机运行在2 N·m和8 N·m负载工况下电机的三相电流,由于算法基于虚拟双极性信号注入法,没有真正注入相位角偏移信号,不会引入额外的损耗和噪声,因此电机工作在稳态时三相电流均为光滑的正弦波。
4.2 暂态性能研究
为对本算法的暂态性能进行研究,给定电机转速为600 r/min,当给定负载转矩由2 N·m突变至6 N·m时,观察电机的电流幅值、电流矢量相位角的变化情况,并与虚拟单极性方波信号注入法的结果作对比。
图4展示了两种MTPA方法控制下电机电流幅值Is的暂态波形。可以看到,相比于传统的虚拟单极性方波注入法,本算法控制下得到的电流幅值更小,并且随着转矩的增大,电流幅值的减少更显著,性能提升越强。这是因为随着负载的增大,MTPA控制受到电机参数非线性特性的影响更显著,传统虚拟单极性方波信号注入法的误差也变大,而基于同构电感转矩模型算法考虑了电机参数的非线性变化特性,在重载工况下具有更显著的改进效果。

图4 600 r/min变负载下的电流幅值仿真波形
图5展示了在两种MTPA控制方法下电机电流矢量相位角β的暂态响应波形。通过对比可以看出,在负载突变的瞬间,算法自启动机制开启,电流相位角不断迭代,寻找到最优电流相位角后,算法自启动机制关闭,系统进入稳定,算法动态响应快速,具有良好的动态性能。

图5 600 r/min变负载下的电流相位角仿真波形
5 实验验证
为了对基于同构电感重构转矩模型的VSIM进行验证,搭建了SynRM实验台架。台架由控制对象SynRM和对拖负载PMSM组成,两台电机经扭矩传感器连接。PMSM输出的三相电流经整流后连至电子负载,操作电子负载可调整负载转矩的大小。SynRM由SiC逆变器和DSP (TMS320C6657)控制器组成。逆变器直流侧母线电压为300 V。实验SynRM相关参数如表1所示。
5.1 稳态性能研究
与仿真研究的工况一致,实验过程中给定电机转速为600 r/min,在负载转矩分别2 N·m、4 N·m、6 N·m、8 N·m四种工况下测量本算法控制下SynRM的稳态电流幅值,并与传统虚拟单极性方波注入法作比较,如表3所示。
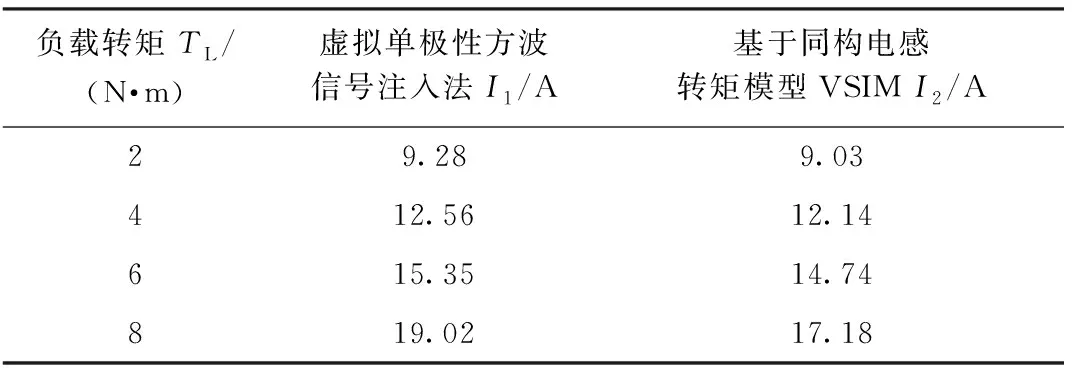
表3 600 r/min下的SynRM稳态电流值实验结果
从表3中可以看出,相比于传统的将电机电感参数视为常数的虚拟单极性方波信号注入法,本算法考虑了参数的非线性特性,具有更精准的转矩模型,实现MTPA控制的稳态精度更高。在给定负载转矩相同的情况下,本算法控制下的电机电流幅值更小,能有效降低铜耗。进一步实验对比也可发现,本算法控制下的电机电流略大于基于电感参数扫描的双极性VSIM,但是失去了繁琐复杂的扫描过程,控制方法更加精简。
5.2 暂态性能研究
在硬件实验中,给定电机转速为600 r/min,令负载转矩从2 N·m突变至6 N·m,观察电机的电流幅值与电流矢量相位角的暂态波形。
图6展示了采用基于同构电感转矩模型VSIM和虚拟单极性方波信号注入法的MTPA控制下电机电流幅值Is的暂态响应波形。可以看到,本算法控制下的电机电流幅值相比虚拟单极性方波注入法减小很多,并且在重载工况下改善效果更明显。当负载突变时,电流幅值能快速进入稳定,具有良好的动态性能。
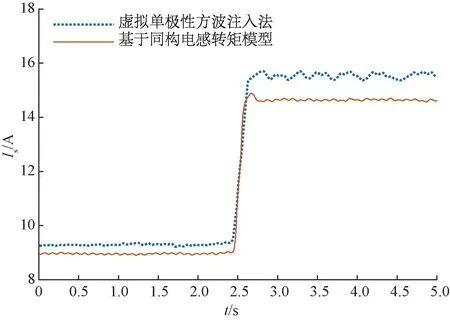
图6 600 r/min变负载下的电流幅值实验波形
图7展示了两种方法控制下电机电流矢量相位角β的暂态响应波形。可以看到,负载突变时,算法自启动机制开启,本算法的电流矢量相位角会产生小幅振荡,但随后快速稳定,算法自启动机制关闭,算法的动态性能良好。
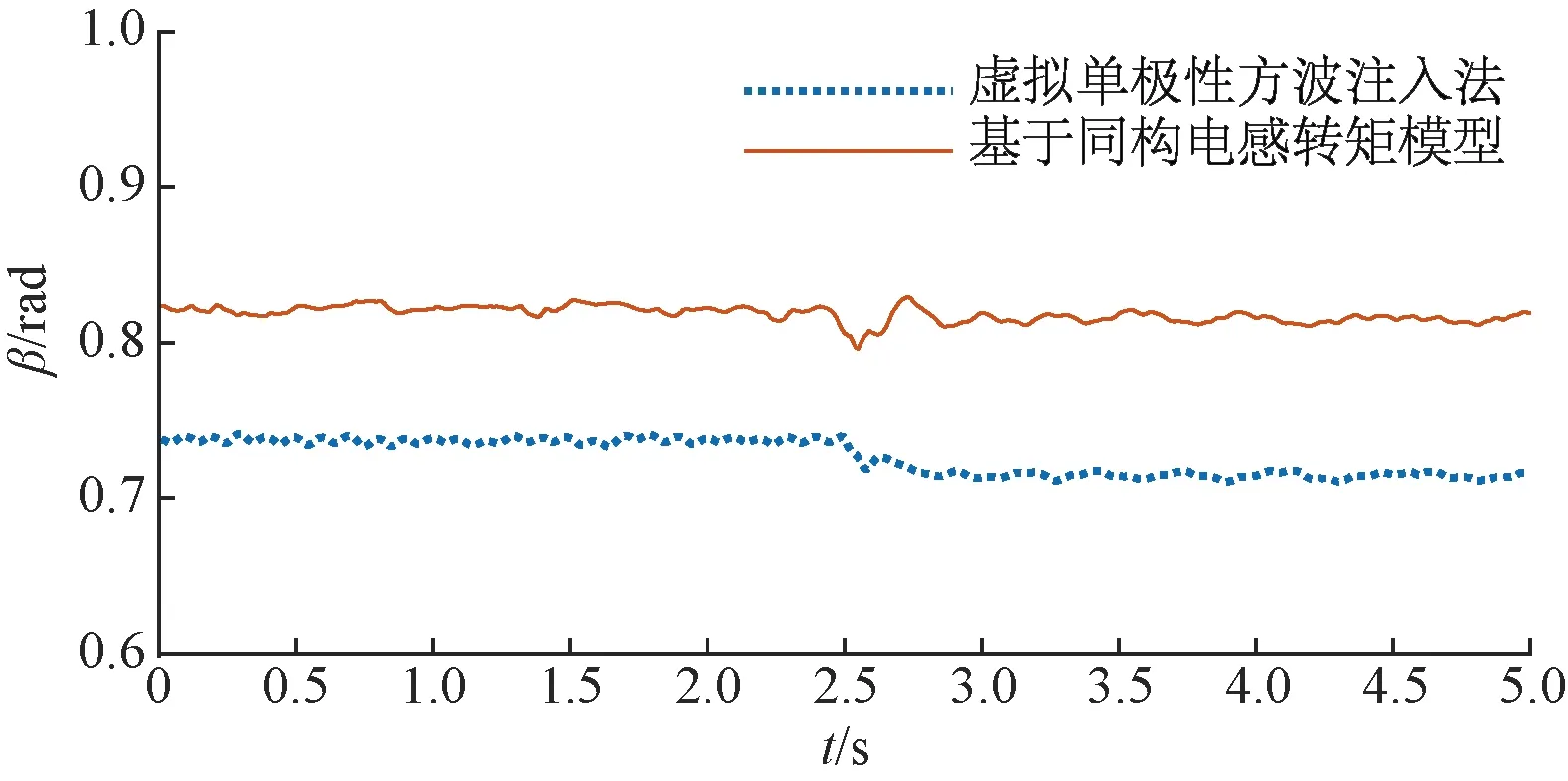
图7 600 r/min变负载下的电流相位角实验波形
从硬件实验与理论仿真的结果可以看到,仿真和实验结果能够互相对应。由于将SynRM参数非线性变化纳入了考量,并重构基于同构电感参数的转矩模型,本方法提升了MTPA控制的稳态精度,并且算法也具有较好的动态响应特性,在负载工况突变的情况下能实现快速精准控制,具有良好的鲁棒性。
6 结 语
本文在虚拟双极性信号注入法的基础上提出了基于同构电感的转矩模型重建方法,配合设计了相位摇摆法策略来自适应观测同构电感参数值。基于同构电感重建的转矩数学模型考虑了电机参数非线性特性,能更为精确地定位MTPA工作点。相位摇摆法在电机某一稳态运行处施加小量相位角偏移形成新稳态,以弥补参数矩阵缺秩的问题。同时相位摇摆法的自启动机制确保电流矢量不会频繁摇摆造成转矩振荡和电流谐波等问题。由于算法未引入额外的高频电信号到实际系统中,因此不会产生额外的损耗与转矩脉动。最后通过SynRM的仿真和实验,验证了基于同构电感转矩模型的虚拟双极性信号注入法的稳态寻优精度,相比于传统的虚拟方波信号注入法有所提高,并且具有良好的动态响应特性。