基于八节点环形网络的任务映射方法研究＊

王楚越，文万志

(南通大学信息科学技术学院，江苏 南通 226000)

0 引言

如今全球高性能计算机飞速发展，由于计算任务繁重，采用一定网络结构将多台计算机连接起来形成高性能计算机集群，在不同的计算机上运行相同的程序，最后需要相互通信。为了提高相连计算机之间的通信效率，减少不必要的跳数，本文从相关数据基础入手，以八节点集群环形网络剖析高性能集群上的计算机程序运行原理，高性能计算集群（MPI）程序指在每一个不同的计算节点上运行同一程序，同时，每一份程序随机分配唯一编号，每一个编号各自所带功能各不相同。在高性能计算集群工作的过程中，编号Rank1 所属的节点会与其余节点产生频繁的通信，但是，除编号Rank1 所属节点外的节点各自互相独立几乎不需要相互通信。通信过程中会产生延迟，节点与节点通信需要经过中间节点中转，产生了跳数，故延长会增大。实际高性能计算程序中时延在总体时间中的比例很大，故而任务映射分配是如何合理分配编号到各个网络节点使得全局计算代价最小的问题。

1 相关工作

随着计算任务的重复性增加，任务映射的分配优化已经成为一个重要问题，而将其运用到高性能计算机集群上提高数据交换效率更是一个最基础的应用。近几年提出的有关任务映射的研究有：PENG 提出的二次雷达识别方式研究[1],LI提出的基于任务映射的暗硅芯片功耗预算方法[2],LIU 提出的一种面向电动汽车控制的AUTOSAR 可运行实体-任务映射方法[3]，Benazir 提出的基于渗透计算的生态系统高效任务映射算法[4]，Imran提出的老年患者健康监护系统采用闭环医疗环境下的智能任务映射机制[5]。本文提出的基于整数规划的任务映射研究是研究基于八节点环形网络，并计算了当多加一条边之后的最优节点分配方案，对比其他方式，通信的效率有所提升，并检验了本文模型具有普适性，这与当前的技术是有所不同的。

2 数据分析模型框架

本文的数据分析模型框架图如图1 所示，本模型主要包含了五个模块：数据预处理、最小二乘法拟合、验证拟合结果、计算全局最小代价、迪杰斯特拉算法计算增加一条边之后的情况。本文使用excel 软件对数据进行预处理，利用mastlab语言对处理好的数据进行最小二乘法[6]拟合，并穷举可能的连接方式，根据得到的某一程序不同Rank之间的通信频次数据，建立数学模型设计合理的任务映射策略，利用matlab 语言计算全局最小代价，最后通过迪杰斯特拉算法计算出增加一条连接边之后的最优的方案，使得网络的最大跳数（直径）最小。

图1 最小二乘法拟合曲线

3 优化模型建立

Rank间的时延与hops数量正相关，故希望构造数学模型分析时延与跳数的关系。利用最小二乘法拟合函数可以清晰地得知时延与跳数的函数关系。分析各节点间时延测试的原始数据记录数据，在原数据表中利用Execl 表自带的函数TRIMMEAN()将相同对应的Rank的不同循环次数所得的时延去掉最大值、最小值，加和求平均，保证数据的准确性和科学性，并且做相应的保存，为最小二乘法拟合做准备（见表1）。

表1 节点Node与Rank对应情况

根据图2、图3 及8 节点环形网络不考虑往返性的特点，可以分析出各Rank间跳数：R1-R4、R1-R2、R4-R3、R2-R6、R3-R7、R6-R8、R8-R5、R7-R5 的跳数为1，R1-R3、R1-R6、R4-R7、R4-R2、R3-R5、R7-R8、R5-R6、R8-R2 的跳数为2，R1-R7、R1-R8、R4-R5、R4-R6、R3-R8、R3-R2、R7-R6、R5-R2 的跳数为3，R1-R5、R4-R8、R3-R6、R7-R2的跳数为4。

求平均值公式如下：

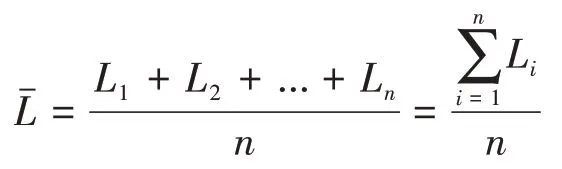
利用最小二乘法对已求得的平均值及其所对应的跳数进行拟合，最小二乘法原理的公式如下：

最终拟合曲线函数表达式：

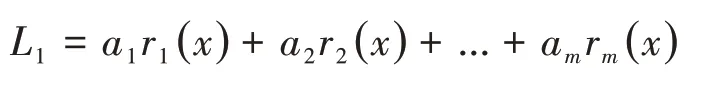
在直观判断的基础上，选几种曲线分别拟合，然后比较，选取最小二乘指标J 最小的函数作为最终的数学模型。

根据已得数据进行代码求解，通过对拟合次数的调整，本文进行四次拟合，最终选择最小的最小二乘指标值，经检验其误差为最小，接着借助代码求解得到结果和一个最合适的最小二乘法拟合曲线。

根据输出结果可以得出时延(L)与跳数(H)的关系为：

在实际的高性能计算程序中，数据交换产生的延迟占据总体计算时间比例是非常大的，如果两个频繁通信Rank所属的节点之间延迟较大，而两个较少产生通信Rank所属的节点之间延迟较小，就会导致整个计算过程变长，因此，为了尽可能地减少计算代价，本文建立以下数学模型。

由于数据规模的有限性，所以选择用穷举法对每一种Rank 的分配情况进行对比求出最小，计算代价(cost)=通信频次×跳数，公式如下：

考虑到通信频次往返的相同性，首先根据计算代价（cost）与通信频次和跳数的函数关系运用穷举法，得出编号和节点合理的任务映射策略，使得全局计算代价最小，提高程序的计算速度。图2 为求最小代价rank分配的流程图。

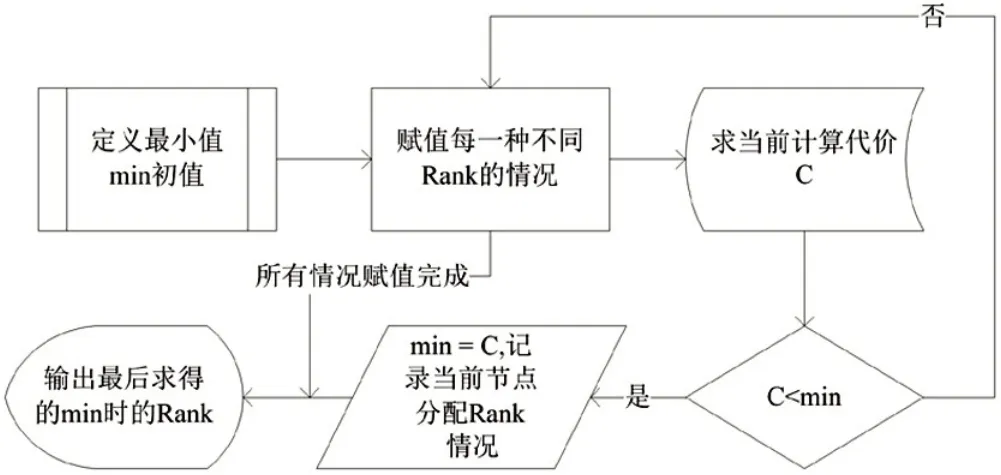
图2 求最小代价流程图

求解前，先总结出基于八节点环形网络各节点Node 到其他节点的跳数,利用穷举法，代码实现数学模型，得出编号和节点合理的任务映射策略。

本文通过模型求解可知，全局最小计算代价min为2.9514，各节点分配Rank情况如表2。

表2 各个节点分配Rank情况

从前面所得结论中，我们发现由于环形网络跳数与效率呈负相关关系，因此为寻求效率高的最优方案，本文建立以下模型。

考虑到要在每个节点上增加额外一条边并保持节点的数目不变的条件下可以假设0-1 变量，xij表示节点i与节点j是否相连，构造0-1整数规划模型，利用Dijkstra算法，找寻某一网络拓扑结构中某一点到其他所有点的最短路径中的最大跳数，并对比每一个结构找到每一张图的最短路径中的最大跳数中的最小值，以寻求最优方案，得到网络的最大跳数的最小数学模型。

由于所求为跳数的最小值，首先基于0-1 整数规划模型创建如下表达式：

此题可抽象为寻找图中从某一点到其他所有点的最短路径求解的图论问题，因此本文选择基于Dijkstra算法，计算一个节点到其他所有节点的最短路径。以起始点为中心，向外层扩展，直到扩展到终点为止，其时间复杂度为O（n2），并采用贪心算法的策略求解此类问题。

根据上述表达式构建邻接矩阵，本文取其中一种情况作为例子展现邻接矩阵的构造，如图3所示。

图3 分配方案例图

其邻接矩阵对应如下：

图4为求解流程图，首先，通过穷举法依次列出所有邻接矩阵的情况，此时在已知邻接矩阵的条件下，通过遍历已知图的所有路径，运用dis 数组记录到第i点的最短路径，然后在循环中进行大小的比较判定。同时，利用已初始化为零的mark 数组作为标记数组，判断是否已经遍历过，最终输出最优分配方案。

图4 求解流程图

从中可以得出在八节点集群环形网络中，最大跳数（直径）的最小值为2。

4 结果分析与检验

基于已归纳完成的数学模型，将原始数据输入测试模型的准确性，测试结果数据见表3。

表3 原始值与测试值对比

5 结论

本文提出了一种基于八节点环形网络的任务映射分配优化问题，使用了最小二乘法、数据拟合、迪杰斯特拉算法、整数规划等方法，对所搜集到的数据进行整合计算，并给出网络节点的最优分配方案，最终通过将原本已知数据带入求出的表达式对比原始数据，发现数据吻合度高达99%，验证了本文的模型具有普适性，网络节点的最优方案求得全局最小计算代价min 为2.9514，对比原本其他方案有明显提升，验证了本文方法的有效性。

本文的实验虽然具有一定的实际数据的支撑，但是基于八节点环形网络还有更为复杂的计算过程，本文的全局最小计算代价还有进一步提升空间，下一步将着手于提升整体方法的简化性，进一步提升八节点环形网络计算效率，从而使此方法具有普适性。